2025_11_5_刷题

2025_11_5_刷题

一、前言

刷题这件事搁置了很久了，终于决定逼自己一把了。

我知道刷题太重要了，近期一直在看数据结构，其实很早就开始看了，6月-11月一直在学，当然之间还搞了杂七杂八的东西。刷题这件事一直时断时续。11月本来想开始，无奈学校作业太多，一直到今天。今天开始，我要发力了，我相信自己都能兼顾到。。。数据结构的复习也已进行了大半了，此时刷算法题刻不容缓。。。

OK，总结完毕，来看看今天刷了哪些题吧~
在有效刷题这件事上，我可以说，我纯小白。刚开始的题目可能对于在座各位很简单，但是我仍然可以学很久。。。想法可以说是很浅显稚嫩，见谅~

二、刷题

2.1 农作物丰收竞赛

---

------计挑赛2024年C++组真题

在一个农业大国，每年都会举行一次盛大的农作物丰收竞赛，农民们将自己种植的庄稼进行收割，并按照产量排名，争夺丰收冠军的称号。参赛的农民需要连续数天展示自己的农作物产量，最终以累积的总产量决定最终的胜利者。

今年的丰收竞赛进入了最后一天，前几天的比赛中，农民们已经累积了各自的收成。然而，最后一天的产量将会是决定性的，因为当天的产量将以特别规则计算得分：当天的第一名农民将获得 N 点得分，第二名将获得 N-1 点得分，依次类推，最后一名将获得 1 点得分。最后一天的得分，没有并列的情况出现。

现给定当前每位农民的累积得分，计算在最后一天比赛开始前，有多少位农民仍然有可能通过最后一天的比赛获得最终的丰收冠军（最终总冠军有可能存在并列）。

输入格式:

• 第一行输入一个整数 N，表示参赛农民的总数。

• 接下来的 N 行分别输入N位农民当前的累积得分。

输出格式：

输出一个整数，表示有多少位农民仍然有可能获得最终的丰收冠军。

输入样例1：

3

8

10

9

输出样例1：

3
输入样例2：

6

60

55

50

30

20

10

输出样例2：

2

2.1.1 分析题目

农民先前已经有了一定的累计积分，最后一天的积分随人头递减，根据得分情况确定最终冠军。

最终谁都有机会得冠军，且冠军可以并列。

题目让求最终冠军最多可以有多少人。

2.1.2 思维发散

我的想法是对所有人先前得分进行排序，让初始积分最少的人得最多分，然后依次根据排名逆行赋分。但是这样分配，对于第二个样例（先前积分最高和最低差距甚大）的情况不满足。我一时也想不出来，看来答案才深觉天地之宽。

2.1.3 思路整理

• 排序------sort

• 循环用一个新的数组存放最后一次积分后的数据★

• 确定新数组的最大值

• 针对原始数据加上最大值看能否达到最大值，统计答案★

2.1.4 代码

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,a[300005],b[300005],ans,m;
int main()
{
    // 输入
    scanf("%d",&n);
    for(int i = 1; i <= n; ++i)
    {
        scanf("%d",&a[i]);
    }
    // 排序
    sort(a+1, a+n+1);
    // 统计最终积分
    for(int i = 1; i <= n; ++i)
    {
        b[i] = a[i] + n - i + 1;
    }
    // 选出最大值
    m = *max_element(b + 1, b + n + 1);
    // 统计答案
    for(int i = n; i >= 1; i--)
    {
        if(a[i] + n >= m)
        {
            ans++;
        }
        // 注意是从大到小依次循环的
        // 如果得分较高的没有希望得第一，那么分低的更没希望
        // 这种处理，优化了时间复杂度
        else
        {
        	break;
		}
    }
    printf("%d\n",ans);
    return 0;
}

2.1.4 总结

• 仔细看这段代码，其实它所用的方法是贪心的思想------只考虑最终得分，排名越靠前，原始值越小，最终的额外加分就越多。没有通过遍历尝试所有可能到达高分的元素个数。
• 最后一步的处理，术语称作"剪枝"。

2.2 修复公路

---

------计挑赛2024年C++组真题

在一个风景如画的国家，著名的"黄金大道"连接着各个旅游景点。然而，随着游客数量的激增，这条大道出现了许多破损路段，影响了游客的行程。为了确保游客的安全和顺利通行，国家决定对这些破损路段进行修复，并在某些路段实施临时封闭。你作为负责交通管理的工程师，需要计算出最少需要封闭的路段总长度，以便尽快修复这些问题区域。

现给定 n 个破损路段的坐标和需要实施封闭的路段数量 m，要求找到一种分配方案，使得封闭的路段总长度最小。

输入格式：

• 第一行包含两个正整数 n 和 m（中间使用一个空格符隔开，m后不许有空格）。

• 第二行包含 n 个整数，表示破损路段的坐标（坐标值为长整型，且按从小到大的顺序给出，且不会有两个点坐标相同）（n个整数之间使用一个空格符隔开，最后一个整数后不许有空格）。

输出格式：

输出一个整数，表示最小的封闭路段总长度。

输入样例1：

18 4

3 4 6 8 14 15 16 17 21 25 26 27 30 31 40 41 42 43

输出样例1：

25

样例1说明：

封闭的路段为：3-8、14-21、25-31、40-43，最小的封闭路段总长度为6+8+7+4=25。

提示：路段3-8的封闭情况如下图所示。

输入样例2：

8 4

2 5 6 7 11 12 15 20

输出样例2：

10

2.2.1 分析题目

将一个很长的破损路段进行截断，分为有限个小路段进行整修，使这些路段加起来之和最小。

2.2.2 思维发散

我想，题目主要目的在于划分路段 ，一段路划多少才合适？我没有头绪，我开始看样例，企图能找到眉目。划分的关键在于相邻路段的距离之差。

2.2.3 整理思路

• 统计相邻路段的距离之差，选取最大的m个差值，作为划分的依据
• 统计划分之后的路段之和

2.2.4 代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#define ll long long
ll n, m,a[15005],b[15005],sum;
int main()
{
    scanf("lld %lld", &n, &m);
    for(int i = 0; i < n; i++)
    {
        scanf("%lld", &a[i]);
    }
    for(int i = 1; i < n; i++)
    {
        b[i] = a[i] - a[i-1];
    }
    sort(b, b + n);
    // 分成m段，去除m - 1段最大的距离
    for(int i = 0; i < n - m + 1; i++)
    {
        sum += b[i];
    }
    // 为什么+m呢，可以仔细看一下样例，一段路的计算是尾-首+1
    printf("%lld", sum + m);
    return 0;
}

2.2.5 总结

• 这里难点在于某个从小错到大的误区：分成m段，在循环中就是排除m - 1段最大的距离。
• 在计算路程时是首 - 尾 + 1。

2.3 限时抢购

---

小明来到了超市，正在进行限时抢购活动。在这次活动中，他可以在限定时间内尽可能多地把自己喜欢的商品放进购物车，而不需要花费一分钱。购物车的最大承重为 W，他希望在不超载的情况下，尽可能获取价值最大的商品。

超市中有 n 种商品，每种商品的价值为 vi，重量为 wi，每种商品的数量为 mi。小明的目标是选择一些商品，使购物车的总重量不超过 W，同时获取的商品总价值最大。

输入格式:

· 第一行包含两个整数 n 和 W，分别表示商品种类的数量和购物车的最大承重（n和W中间使用一个空格隔开）。

· 接下来的 n行，每行包含三个整数vi、wi、mi，分别表示第 i 种商品的价值、重量和数量（每一行的vi、wi、mi中间使用一个空格隔开，mi后不可有空格）。

输出格式：

输出一个整数，表示在不超载的情况下，小明能够获取的最大商品总价值。

输入样例1：

4 20

3 9 3

5 9 1

9 4 2

8 1 3

输出样例1：

47

输入样例2：

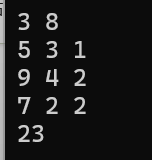
3 8

5 3 1

9 4 2

7 2 2

23

输出样例2：

23

2.3.1 分析题目

看到这个题目，我就知道是背包问题的板子题，但是很无奈我忘记怎么做了。。。

2.3.2 思维发散

快让我搜索一下。。。

背包问题：

• 01背包：每种物品只有一个
• 完全背包：每种物品有无数个
• 多重背包：不同种物品的数量不同
• 分组背包：按组打包，每组最多选一个。

很明显这里属于多重背包。

2.3.3 整理思路

直接套板子

2.3.4 代码

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n, W, v[505], w[505], m[505], dp[60005];
int main()
{
    // 输入
    cin >> n >> W;
    for(int i = 1; i <= n; i++)
    {
        cin >> v[i] >> w[i] >> m[i];
    }
    //多重背包
    // 遍历物品种类
    for(int i = 1; i <= n; i++)
    {
        // 遍历物品重量
        for(int j = W; j >= w[i]; j--)
        {
        	// 遍历物品数量
            for(int k = 1; k * w[i] <= j && k <= m[i]; k++)
            {
                dp[j] = max(dp[j], dp[j - k * w[i]] + k * v[i]);
            }
        }
    }
    cout << dp[W] << endl;
    return 0;
}

为什么j要倒着遍历？

在算后面的值时会用到前面的值，如果正着的话会导致前面的值被更新，但是后面的值没有被更新，前面的物品会放很多次（恰好这为完全背包提供了思路）

2.3.5 总结

背包问题应该回炉重造了。。。

三、小结

今日份刷题就到这里吧~后面的路任重道远