力扣每日一题（四）线段树 + 树状数组 + 差分

目录

[1526. 形成目标数组的子数组最少增加次数 -- 序列差分](#1526. 形成目标数组的子数组最少增加次数 -- 序列差分)

[3479. 水果成篮 III -- 线段树](#3479. 水果成篮 III -- 线段树)

[2179. 统计数组中好三元组数目 -- 树状数组](#2179. 统计数组中好三元组数目 -- 树状数组)

[面试题 03.02. 栈的最小值 -- 额外开数据结构](#面试题 03.02. 栈的最小值 -- 额外开数据结构)

[910. 最小差值 II -- 思路题](#910. 最小差值 II -- 思路题)

[3244. 新增道路查询后的最短距离 II -- 思路题](#3244. 新增道路查询后的最短距离 II -- 思路题)

[3243. 新增道路查询后的最短距离 I](#3243. 新增道路查询后的最短距离 I)

---

1526. 形成目标数组的子数组最少增加次数 -- 序列差分

题面：每次令一个区间增加 1，从全 0 数组 到目标数组（全为正）的最少操作次数。

区间 +1，联想到每次给差分数组一个位置 +1，一个位置 -1。

即由 初始全为0 的差分数组到目标差分数组。

从第一个 +1开始，每次消掉一个 +1 和后面的一个 -1。

并且由于目标数组全为正，能保证从前开始消 +1，没有多余的 -1 没被消。

最后答案即为差分数组的正数值之和（消 +1的次数）

class Solution:
    def minNumberOperations(self, target: List[int]) -> int:
        return target[0] + sum(max(y - x, 0) for x, y in pairwise(target))

3479. 水果成篮 III -- 线段树

fruits = [4,2,5], baskets = [3,5,4]

把水果按顺序，找最前面的 放得下的篮子。

线段树维护 baskets 区间最大值（最大的篮子）

如果整棵子树的最大容量都小于 x，说明没有这样的篮子，返回 −1。

否则，先递归左子树。如果左子树没找到（左子树的最大值小于 x），再递归右子树。

如果我们能递归到线段树的叶子，说明找到目标篮子，返回叶子对应的篮子下标。

class SegmentTree:
    def __init__(self, a: List[int]):
        n = len(a)
        self.max = [0] * (2 << (n - 1).bit_length())
        self.build(a, 1, 0, n - 1)

    def maintain(self, o: int):
        self.max[o] = max(self.max[o * 2], self.max[o * 2 + 1])

    # 初始化线段树
    def build(self, a: List[int], o: int, l: int, r: int):
        if l == r:
            self.max[o] = a[l]
            return
        m = (l + r) // 2
        self.build(a, o * 2, l, m)
        self.build(a, o * 2 + 1, m + 1, r)
        self.maintain(o)

    # 找区间内的第一个 >= x 的数，并更新为 -1，返回这个数的下标（没有则返回 -1）
    def find_first_and_update(self, o: int, l: int, r: int, x: int) -> int:
        if self.max[o] < x:  # 区间没有 >= x 的数
            return -1
        if l == r:
            self.max[o] = -1  # 更新为 -1，表示不能放水果
            return l
        m = (l + r) // 2
        i = self.find_first_and_update(o * 2, l, m, x)  # 先递归左子树
        if i < 0:  # 左子树没找到
            i = self.find_first_and_update(o * 2 + 1, m + 1, r, x)  # 再递归右子树
        self.maintain(o)
        return i


class Solution:
    def numOfUnplacedFruits(self, fruits: List[int], baskets: List[int]) -> int:
        t = SegmentTree(baskets)
        n = len(baskets)
        ans = 0
        for x in fruits:
            if t.find_first_and_update(1, 0, n - 1, x) < 0:
                ans += 1
        return ans

2179. 统计数组中好三元组数目 -- 树状数组

映射 + 枚举中间 + 树状数组统计前面

两个 0~n-1 的排列，同序的三元组数目。

nums1 = [2,0,1,3], nums2 = [0,1,2,3]

如上两个数组中 都是 0 -> 1 -> 3 的左右顺序。

类似最长公共子数列的思想，按照第一个数组的顺序 对第二个数组进行map， 递增 == 公共。

nums1 = [4,0,1,3,2], nums2 = [4,1,0,2,3]

映射得到一个单调递增的排列 A=[0,1,2,3,4]。可以得到一个新的排列 B=[0,2,1,4,3]。

递增三元组，枚举中间值 y，只需知道 前有多少 < y；后有多少 > y。

若前有less个小于y的，左边大于y的为 i - less 个，大于 y的一共 n-1-y个。

所以右边大于y的为 n-1-y-i+less 个。

所以得到 less 后，乘积为 less*(n-1-y-i+less)。

数从 [0,n-1] 后移到 [1,n]，树状数组统计 y 前记录了多少个数。

class FenwickTree:
    def __init__(self, n: int):
        self.tree = [0] * (n + 1)  # 使用下标 1 到 n

    def update(self, i: int) -> None:
        while i < len(self.tree):
            self.tree[i] += 1
            i += i & -i

    def pre(self, i: int) -> int: # 向前统计有多少数
        res = 0
        while i > 0:
            res += self.tree[i]
            i &= i - 1
        return res

class Solution:
    def goodTriplets(self, nums1: List[int], nums2: List[int]) -> int:
        n = len(nums1)
        p = [0] * n
        for i, x in enumerate(nums1):
            p[x] = i # 映射

        ans = 0
        t = FenwickTree(n)
        for i, y in enumerate(nums2):
            y = p[y] # 映射
            less = t.pre(y)
            ans += less * (n - 1 - y - (i - less))
            t.update(y + 1)
        return ans

面试题 03.02. 栈的最小值 -- 额外开数据结构

在华为 AI 算法工程师一面手搓。

请设计一个栈，除了常规栈支持的 pop 与 push 函数以外，还支持min函数，该函数返回栈元素中的最小值。

并且最小值 需要O(1) 不能通过遍历。

因为栈相当于在前缀的基础上往后加 元素，可以额外开一个 辅助最小栈 ，记录当前前缀最小值。

栈顶元素就一直是 当前栈的最小值，新加入元素 只需 val 和 minn[-1] 比较。

class MinStack:
    def __init__(self):
        self.st = [0]
        self.minn = [inf]
        
    def push(self, x: int) -> None:
        self.st.append(x)
        self.minn.append(min(self.minn[-1],x))

    def pop(self) -> None:
        self.st.pop()
        self.minn.pop()

    def top(self) -> int:
        return self.st[-1]

    def getMin(self) -> int:
        return self.minn[-1]

910. 最小差值 II -- 思路题

先把 nums 排序，如果让大的数还 +k，小的数还 -k，这个分数值会更大。

所以考虑枚举分界线，分界线之上的所有点 -k，之下的所有点 +k。

最后的最大值，由最大值 -k，和之下的最大值 +k产生；最小值同理。

class Solution:
    def smallestRangeII(self, a: List[int], k: int) -> int:
        a.sort()
        ans=a[-1]-a[0]
        for i in range(len(a)-1):
            ans=min(ans,max(a[-1]-k,a[i]+k)-min(a[0]+k,a[i+1]-k))
        return ans

3244. 新增道路查询后的最短距离 II -- 思路题

初始每个道路指向下一个（一条链）后续加新的路，每次输出一个现在从头到尾的最短距离。

条件：任意两次加路 (u,v) 不会存在 u1<u2<v1<v2 （即道路交叉的情况）

分析：意味着 只可能相离或者包容。所以每次走 不被包容的最大步子。

每次来新路的时候，对原先的贡献就是，这一段原来的步数 -1。（只需一次跨域）

class Solution:
    def shortestDistanceAfterQueries(self, n: int, queries: List[List[int]]) -> List[int]:
        nxt = [i + 1 for i in range(n)]
        ans, dist = [], n - 1
        for query in queries:
            k = nxt[query[0]]
            if k < query[1] and k != -1: # 包容以前的，现在大跨度，可以更新
                nxt[query[0]] = query[1]
            # 循环往后指，并且步骤数--
            while k != -1 and k < query[1]:
                nxt[k], k = -1, nxt[k]
                dist -= 1
            ans.append(dist)
        return ans

3243. 新增道路查询后的最短距离 I -- 思路题

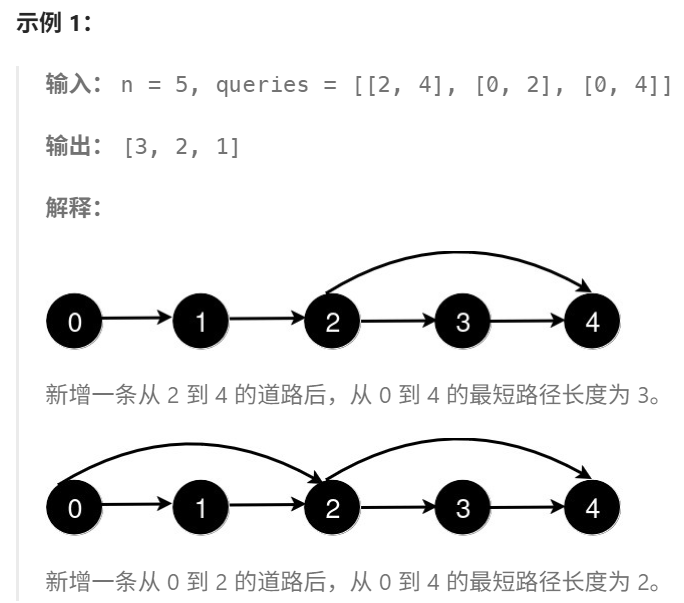
和上一问类似，不过没有（不交叉）的约束条件，并且数据规模缩小。

用 pre 存某个点的前驱 （可以从哪些位置转移过来）；dp 存到某个点的最短距离。

dp 的更新：

1. (u,v) 的影响只会对，走(u,v)的，也就是只可能 v 及以后的位置产生影响。

2. 状态转移 由 min( dp[ pre[j] ]+1 ) 枚举哪个前驱跳过来。

class Solution:
    def shortestDistanceAfterQueries(self, n: int, queries: List[List[int]]) -> List[int]:
        pre=[[i-1] for i in range(n)]
        dp=[i for i in range(n)]
        ans=[]
        for (x,y) in queries:
            pre[y].append(x)
            # 后面的点影响
            for v in range(y,n):
                for u in pre[v]: # 枚举前驱
                    dp[v]=min(dp[v],dp[u]+1)
            ans.append(dp[n-1])
        return ans