链表相关的算法题（2）

1、确定链表是否有环
2、寻找环头

1、确定链表是否有环

题目链接

既然是判断环形指针，我们就可以利用快慢指针。

实际上，慢指针走一步，无论快指针走多少步（大于1步），快慢指针都会在环中相遇。这里我们规定快指针走两步，并简单解释原理：

快指针走两步，慢指针走一步，相差1步
当慢指针走到环的头节点时，快指针已经在环中
但快慢指针的距离，一定是差值的倍数（1的倍数），所以，快慢指针，一定能在环中相遇

代码演示：

c 复制代码

struct ListNode {
    int val;
    struct ListNode *next;
};
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) {
    //找相遇点
    ListNode* slow = head;
    ListNode* fast = head;
    while (fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast)
        {
            //相遇，有环
            return true;
        }
    }
    //出循环，无环
    return false;
}

2、寻找环头

题目链接

在这里，我们需知道一个结论：

如果使用快慢指针，快指针走两步，慢指针走一步。当快慢指针在环中相遇，相遇点到环头节点的距离，等于链表头节点到环头结点的距离。

下面给出证明：

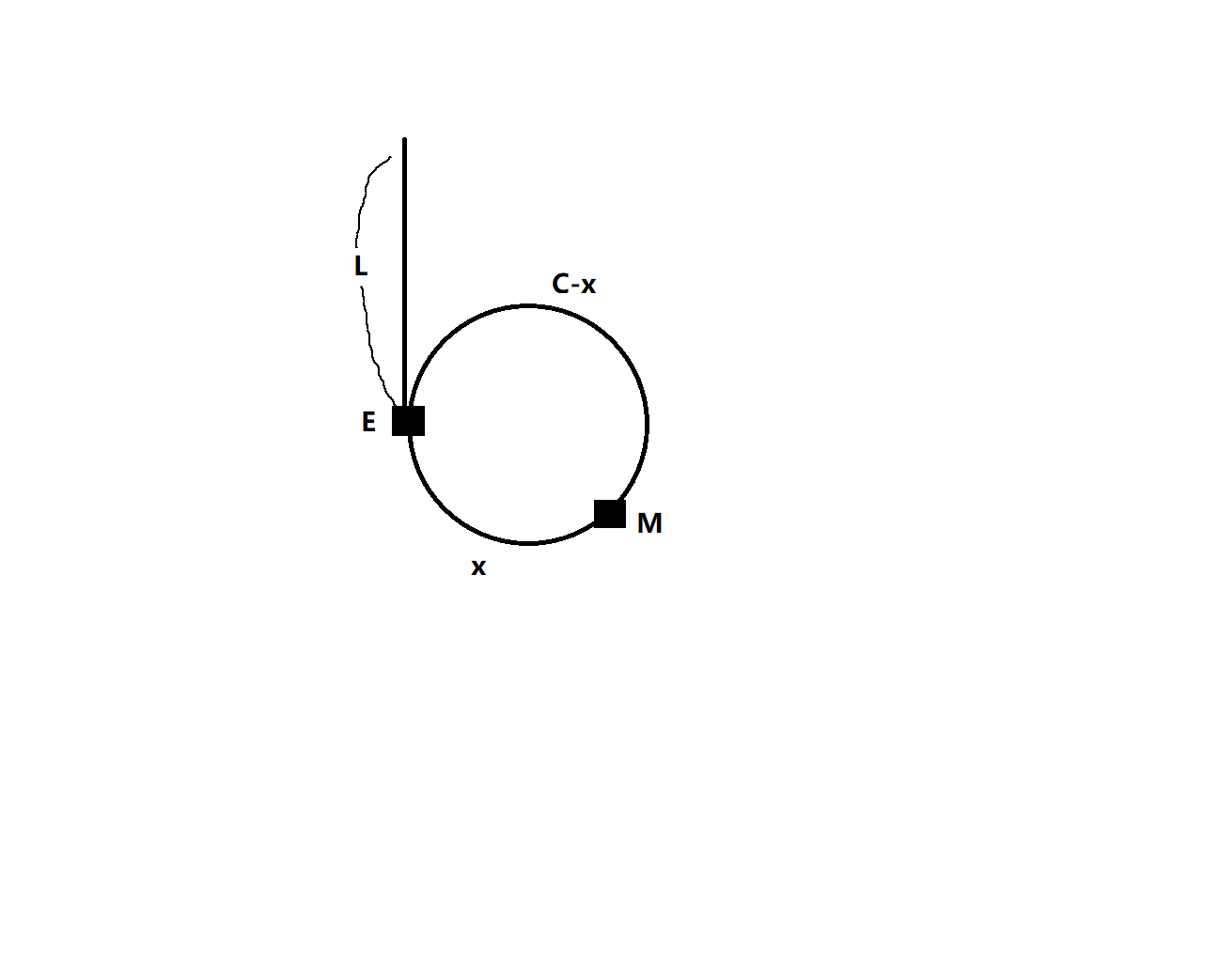
其中，

E是环头结点的位置，M是快慢指针相遇的位置。指针运动的方向为逆时针
L为链表头节点到环头节点的距离
C为环形链表总长度
x为环头节点到相遇位置的距离，C-x为相遇位置返回到环头节点的距离

问题变为了：证明L等于C-x。

当快慢指针相遇，慢指针走过的距离：
x 1 = L + x x1 = L + x x1=L+x

快指针有可能转了几圈，才相遇。快指针走过的距离：
x 2 = L + x + n C ( n > = 1 ) x2 = L + x + nC (n>=1) x2=L+x+nC(n>=1)

又有快慢指针距离关系：
x 2 = 2 ∗ x 1 x2 = 2 * x1 x2=2∗x1

得：
2 ∗ ( L + x ) = L + x + n C ( n > = 1 ) 2 * (L + x) = L + x + nC (n>=1) 2∗(L+x)=L+x+nC(n>=1)

化简，移项，得：
L = n C − x ( n > = 1 ) L = nC - x (n>=1) L=nC−x(n>=1)

凑C - x ，得：
L = ( n − 1 ) C + C − x ( n > = 1 ) L = (n-1)C + C - x (n>=1) L=(n−1)C+C−x(n>=1)

在环内，相差环长度的倍数，就是相遇。所以在环内，L等于C-x，得证。

代码演示：

c 复制代码

struct ListNode {
    int val;
    struct ListNode *next;
};
typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head) {
    ListNode* slow = head;
    ListNode* fast = head;
    while (fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast)
        {
            ListNode* pcur = head;
            while (pcur && slow)
            {
                if (pcur == slow)
                {
                    return pcur;
                }
                pcur = pcur->next;
                slow = slow->next;
            }
        }
    }
    return NULL;
}