神经网络------ 人工神经网络
01 基本概念
核心研究对象
了解大脑新皮层中单个神经元如何处理从其他神经元接收的约1万个突触输入信号。新皮层是大脑在进化过程中最新形成的部分,也是人类大部分思维活动的发生地。
新皮层的神经元与突触规模
新皮层中的神经元数量和神经元间的突触连接数量极为惊人:约有200亿个神经元,每个神经元与其他神经元的连接数约为1万个。相比之下,人类稳定社交网络的规模估计仅为150-200人。
大脑信息处理的关键特性
- 在上述规模下,单个神经元对其他神经元的影响相对较小。
- 大脑的学习过程并不要求单个神经元具备复杂功能------只需通过相对简单的信息整合方式,即可实现两点核心目标:(1)准确描述神经元的响应特性;(2)在聚合神经网络层面实现复杂的信息处理。
大卫·马尔的认知研究三层次理论(1977年提出)
大卫·马尔(David Marr)认为,可从三个相对独立的层次研究认知:
- 计算层(Computational):需完成哪些计算?需处理哪些信息?
- 算法层(Algorithmic):从信息处理步骤的角度看,这些计算是如何实现的?
- 实现层(Implementational):硬件如何实际实现这些算法?
02 大脑功能
大脑的学习功能
感知输入与认知输出
- 感知输入来源:眼睛(视觉)、耳朵(听觉)、鼻子(嗅觉)、手指(触觉)、舌头(味觉)等。
- 认知输出形式 :
- 记忆:长期记忆(如姓名与事实回忆)、工作记忆
- 理解:阅读、聆听与理解、听觉处理、视觉处理
- 逻辑与推理:逻辑推理、数学运算(如长除法)、拼写、数学应用题
- 其他:填字游戏、纸牌游戏、写作、日程安排、决策、足球与棒球运动等
主要脑区及其功能
| 脑区 | 核心功能 |
|---|---|
| 海马区(Hippocampus) | 属于"古老皮层"(原脑皮层),在学习日常事件记忆和事实记忆中起关键作用。 |
| 杏仁核(Amygdala) | 负责识别具有情感显著性的刺激,并向大脑其他区域发出警报;在基于奖励(和惩罚)强化运动(及认知)行为中至关重要。 |
| 丘脑(Thalamus) | 为感觉信息传递至新皮层提供主要通路,同时在注意力、感知、唤醒、运动控制及强化学习等调节功能中可能起重要作用。 |
| 基底核(Basal Ganglia) | 由多个皮质下区域组成,在运动控制、强化学习和执行功能中起关键作用;负责对皮层提出的特定动作做出最终"执行"决策,并决定是否更新前额叶皮层中的认知计划。 |
| 小脑(Cerebellum) | 包含大脑中一半的神经元,主要负责运动协调;在多数认知任务中也会激活,但其在认知中的具体功能仍有待深入研究。 |
新皮层的主要脑叶及其功能
新皮层的结构可通过布罗德曼分区(由Korbinian Brodmann基于解剖差异划分,主要依据不同皮层层的厚度差异)进行界定,各脑叶功能如下:
-
枕叶(Occipital Lobe)
包含初级视觉皮层(V1,位于新皮层的最后端)及从V1向前延伸的高级视觉区域,主要功能是视觉处理。
-
颞叶(Temporal Lobe)
是语义知识的存储地(包含对事物、事件、姓名、面孔、物体、词语等的理解);负责将物体的视觉外观转化为语言标签(反之亦然),也是学习阅读的关键区域。颞上回包含初级听觉皮层(A1)及相关的高级听觉和语言处理区域。此外,颞叶与人类有意识感知的信息(如事实)密切相关。
-
额叶(Frontal Lobe)
前额叶皮层(PFC)被称为大脑的"执行中枢",负责制定重大计划,并结合基本动机和情绪决定下一步行动;是处理抽象、复杂认知推理的关键区域。额叶的内侧和腹侧区域在情绪和动机调节中尤为重要。
-
顶叶(Parietal Lobe)
负责编码空间位置、数字、数学运算、抽象关系等"复杂认知任务";是视觉信息引导运动行为的主要通路。
03 生物神经元
什么是生物神经元?
生物神经元是构成神经系统的基本功能单位,其结构与信息处理机制是大脑实现认知功能的基础。
生物神经元的结构组成
- 细胞体(Cell Body/Soma):神经元的核心部分,负责整合输入信号。
- 树突(Dendrites):接收来自其他神经元的信号,类似"接收器"。
- 轴突(Axon):传递神经元产生的信号,类似"发射器";部分轴突外包裹髓鞘(Myelin Sheath),可加速信号传递。
- 突触(Synapses):神经元间的信号传递节点,位于轴突末梢与另一神经元的树突之间。
生物神经元的信息处理功能
生物神经元是天然的信息处理器,其各结构的功能分工明确:
- 树突:接收来自其他神经元的信号。
- 细胞体:对输入信号进行汇总整合。
- 轴突:将整合后的信号传递至其他神经元。
- 突触:信号传递的关键节点,学习过程通过突触有效性的电化学变化实现。
- 激活条件:当兴奋性信号超过抑制性信号的阈值时,神经元被激活并产生信号。
生物神经元的信号传递机制
信号传递形式
神经元通过电化学信号传递信息:突触会释放化学递质,这些递质的总和若达到阈值,会触发神经元产生"脉冲"(电信号)。
突触的信号调节作用
突触分为兴奋性突触和抑制性突触,分别增强或减弱信号传递。信号传递的"接收端"为树突,"释放端"为轴突末梢。
信号接收与激活流程
- 神经元通过突触接收来自其他神经元的输入信号(通常为数千个)。
- 输入信号在细胞体内近似汇总。
- 当汇总信号超过阈值时,神经元产生电脉冲,脉冲从细胞体沿轴突传递至下一个(或多个)神经元。
04 人工神经元
神经元如何转化为数学模型?
人工神经元通过数学公式模拟生物神经元的结构与功能,核心是将"输入-整合-输出"过程抽象为可计算的数学关系。
神经元的数学模拟功能
| 生物神经元结构 | 人工神经元对应组件 | 功能描述 |
|---|---|---|
| 树突 | 输入连接(Input Connections) | 接收外部输入信号。 |
| 细胞体 | 节点/单元/处理元素(PE) | 模拟细胞体的信号汇总功能。 |
| 轴突 | 输出连接(Output Connection) | 传递处理后的信号。 |
| 突触 | 偏置函数(Bias Function) | 模拟突触的阈值作用,判断信号是否达到激活条件。 |
| 突触可塑性 | 激活函数与连接权重(Connection Weights) | 通过调整连接权重模拟学习过程,激活函数将汇总信号转换为输出信号。 |
人工神经元的类型
1. 单输入神经元
- 基本功能:接收单个输入信号,通过权重(Weight)调整信号强度,结合偏置(Bias)后经激活函数处理,输出结果。
- 数学关系 :设输入为xxx,权重为www,偏置为bbb,激活函数为fff,则输出a=f(wx+b)a = f(wx + b)a=f(wx+b)。
2. 多输入神经元
- 核心特点 :接收多个输入信号,每个输入对应独立权重,先汇总所有输入与权重的乘积(即∑i=1mxiwi\sum_{i=1}^m x_i w_i∑i=1mxiwi),再结合偏置经激活函数输出。
- 数学关系 :设输入为x1,x2,...,xmx_1, x_2, ..., x_mx1,x2,...,xm,对应权重为w1,w2,...,wmw_1, w_2, ..., w_mw1,w2,...,wm,偏置为bbb,激活函数为fff,则输出a=f(∑i=1mxiwi+b)a = f\left(\sum_{i=1}^m x_i w_i + b\right)a=f(∑i=1mxiwi+b)。
人工神经元的关键特性
-
输入权重的差异性
并非所有输入信号同等重要:每个输入通过不同权重(wiw_iwi)体现重要性,权重越大,对应输入对输出的影响越强。汇总过程即计算所有输入与权重的线性组合(∑xiwi\sum x_i w_i∑xiwi)。
-
信号的非线性转换
输入信号经线性汇总后,需通过激活函数(非线性函数)处理才能传递给下一个神经元,避免多层网络退化为线性模型,从而实现复杂的非线性信息处理。
常见的激活函数
激活函数是人工神经元的核心组件,负责将线性汇总的信号转换为非线性输出,不同激活函数适用于不同场景:
1. 阶跃函数(Step Function)
- 公式 :f(x)=sgn(x)={1x>00x≤0f(x) = \text{sgn}(x) = \begin{cases} 1 & x > 0 \\ 0 & x \leq 0 \end{cases}f(x)=sgn(x)={10x>0x≤0
- 特点:简单的二值输出,适用于简单分类任务,但缺乏梯度信息,不利于多层网络训练。
2. 线性函数(Linear Function)
- 公式 :f(x)=kx+bf(x) = kx + bf(x)=kx+b(kkk为斜率,bbb为截距)
- 特点:输出与输入呈线性关系,但无法处理非线性问题,多层线性网络等价于单层线性网络。
3. Sigmoid函数
- 公式 :f(x)=11+e−kxf(x) = \frac{1}{1 + e^{-kx}}f(x)=1+e−kx1(kkk为增益参数)
- 导数特性 :f′(x)=kf(x)(1−f(x))f'(x) = kf(x)(1 - f(x))f′(x)=kf(x)(1−f(x))
- 特点 :输出范围为[0,1][0,1][0,1],具有平滑的梯度特性,适用于二分类任务的概率输出,但存在梯度消失问题。
4. Tanh函数
- 公式 :f(x)=1−e−kx1+e−kxf(x) = \frac{1 - e^{-kx}}{1 + e^{-kx}}f(x)=1+e−kx1−e−kx
- 特点 :输出范围为[−1,1][-1,1][−1,1],相比Sigmoid函数更接近零均值,梯度特性更优,但仍存在梯度消失问题。
5. 带泄露ReLU函数(Leaky ReLU Function)
- 公式 :f(x)=max(0.01x,x)f(x) = \max(0.01x, x)f(x)=max(0.01x,x)
- 特点 :解决了ReLU函数在负区间梯度为零的问题(负区间保留微小梯度0.01x0.01x0.01x),缓解梯度消失,适用于深层网络。
人工神经元的结构
人工神经元的标准结构包含以下组件:
- 输入(Inputs) :x1,x2,...,xnx_1, x_2, ..., x_nx1,x2,...,xn,对应生物神经元的树突接收信号。
- 权重(Weights) :w1,w2,...,wnw_1, w_2, ..., w_nw1,w2,...,wn,调整各输入的重要性,对应突触的连接强度。
- 偏置节点(Bias Node) :固定输入为1,权重为w0w_0w0,模拟神经元的阈值特性。
- 汇总(Summation) :计算输入与权重的线性组合(含偏置),即∑i=0nwixi\sum_{i=0}^n w_i x_i∑i=0nwixi(x0=1x_0=1x0=1)。
- 激活函数(Activation Function):对汇总结果进行非线性转换,输出神经元的激活值,对应生物神经元的脉冲产生过程。
人工神经元的数学建模
左图为生物神经元的示意图,右图为其对应的数学模型。数学建模的核心是将生物神经元的"信号接收-汇总-传递"过程抽象为:
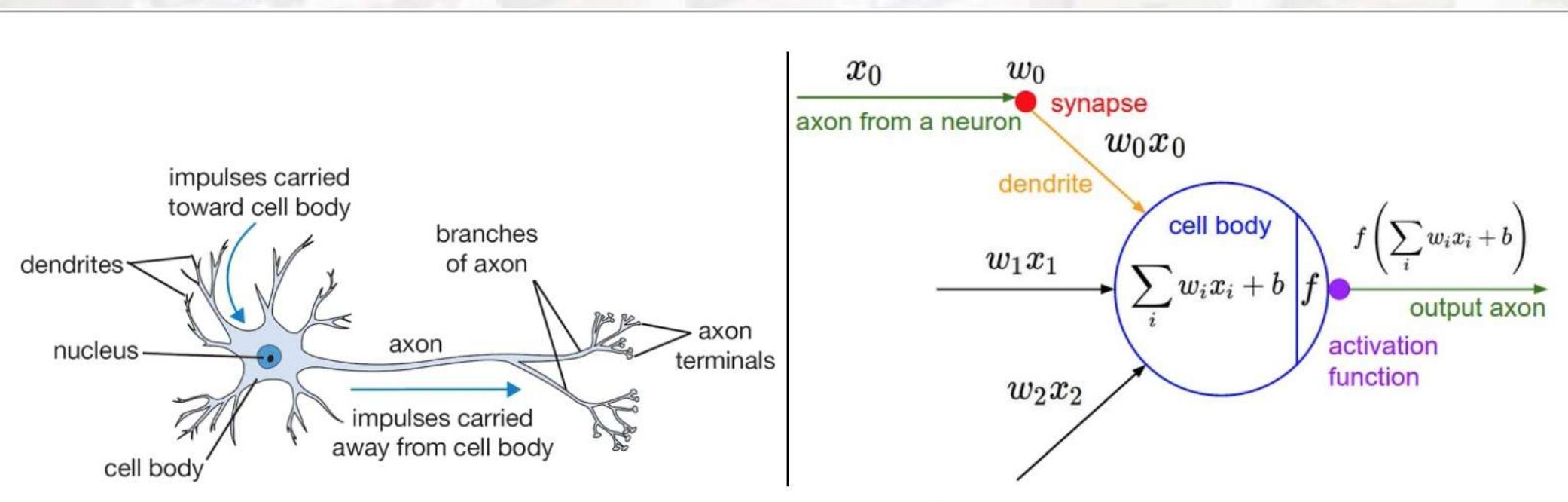
- 输入信号x1,x2,...,xnx_1, x_2, ..., x_nx1,x2,...,xn与对应权重w1,w2,...,wnw_1, w_2, ..., w_nw1,w2,...,wn相乘后汇总,加入偏置项w0w_0w0(偏置节点输入为1)。
- 汇总结果通过激活函数f(⋅)f(\cdot)f(⋅)处理,得到神经元的输出(激活值),即:
Output=f(w0+∑i=1nwixi)=f(wx+b) \text{Output} = f\left(w_0 + \sum_{i=1}^n w_i x_i\right) = f(wx + b) Output=f(w0+i=1∑nwixi)=f(wx+b)
(其中wxwxwx表示输入与权重的线性组合,bbb为偏置,等价于w0w_0w0)。