目录
前言
DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，将簇定义为密度相连点的最大集合，可在噪声数据中发现任意形状的聚类。其核心概念包括Ε邻域、核心对象、密度可达和密度相连，通过参数扫描半径(eps)和最小包含点数(minPts)确定簇结构。该算法通过递归扩展核心对象的邻域形成聚类，无需预设簇数量且对数据顺序不敏感，但参数选择和密度变化会影响结果。DBSCAN可识别噪声点，但在高维数据或密度差异大的数据集中表现较差
算法原理
相关术语
- **密度：**指定半径内点的个数；
- **核心点：**如果某个点的半径邻域epsilon内至少包含minPts个点数，它就是核心点；
- **边界点：**如果一个点既不是核心点，但在某个核心点的epsilon邻域内，则该点是边界点；
- **噪声点：**既不是核心点，也不是边界点；
- **epsilon邻域：**以对象为圆心，epsilon为半径做圆得到的圆形区域称为该对象的epsilon邻域；
DBSCAN的主要特点
1. 无需指定聚类数目 ：与K-means等算法不同，DBSCAN不需要预先指定聚类的数量。
2. 对噪声鲁棒 ：DBSCAN可以识别并处理数据中的噪声点，将它们标记为噪声而不是错误地归入某个聚类。
3. 发现任意形状的聚类：DBSCAN可以识别出任意形状的聚类，而不仅仅是球形或圆形。
DBSCAN算法动态示意图
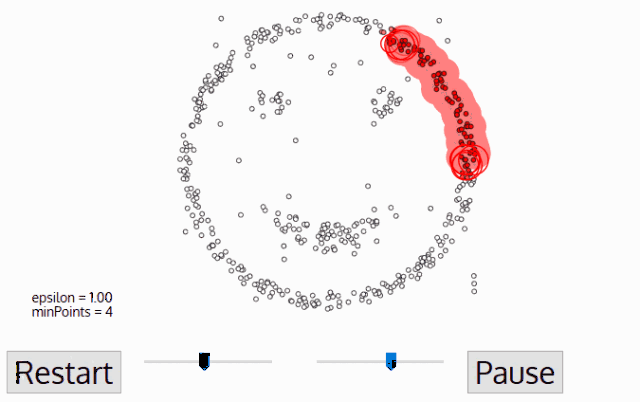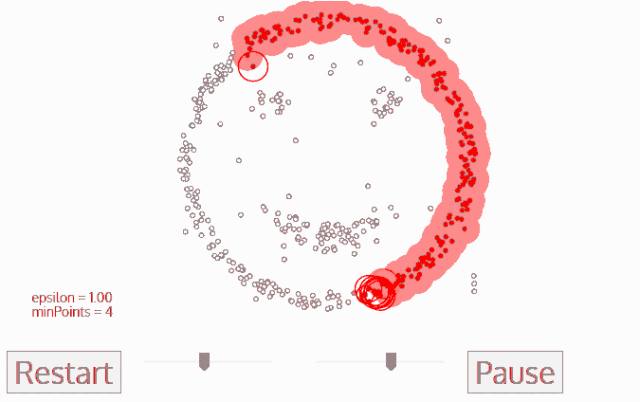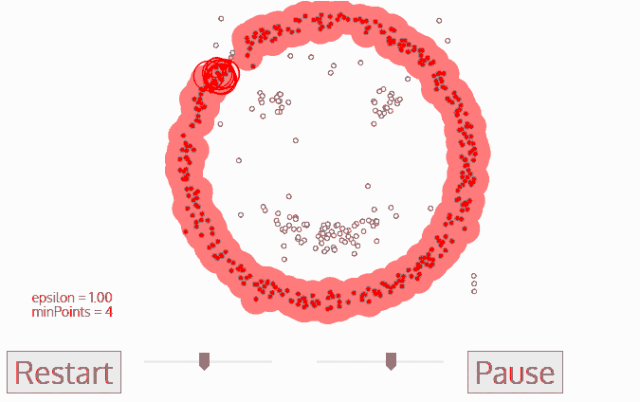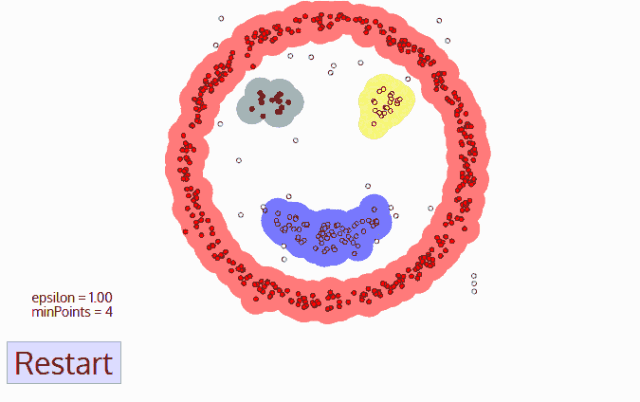
样本点组成
DBSCAN算法处理后的聚类样本点分为：核心点（core points），边界点（border points）和噪声点（noise），这三类样本点的定义如下：
核心点：对某一数据集D，若样本p的-领域内至少包含MinPts个样本（包括样本p），那么样本p称核心点。
即：
假设MinPts=4，如下图的核心点、非核心点与噪声的分布：
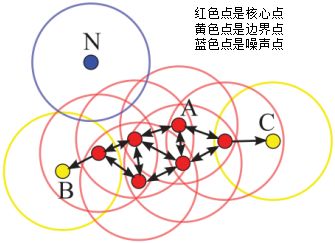
DBSCAN算法划分数据集D为核心点，边界点和噪声点，并按照一定的连接规则组成簇类。介绍连接规则前，先定义下面这几个概念：
密度直达（directly density-reachable）：若q处于p的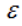
-邻域内，且p为核心点，则称q由p密度直达；
密度可达（density-reachable）：若q处于p的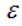
-邻域内，且p，q均为核心点，则称q的邻域点由p密度可达；
密度相连（density-connected）：若p，q均为非核心点，且p，q处于同一个簇类中，则称q与p密度相连。
下图给出了上述概念的直观显示（MinPts）：
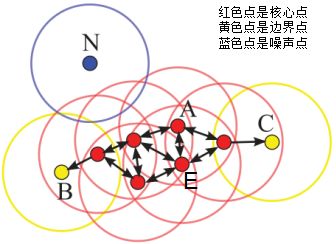
其中核心点E由核心点A密度直达，边界点B由核心点A密度可达，边界点B与边界点C密度相连，N为孤单的噪声点。
DBSCAN是基于密度的聚类算法，原理为：只要任意两个样本点是密度直达或密度可达的关系，那么该两个样本点归为同一簇类，上图的样本点ABCE为同一簇类。因此，DBSCAN算法从数据集D中随机选择一个核心点作为"种子"，由该种子出发确定相应的聚类簇，当遍历完所有核心点时，算法结束。
DBSCAN算法思想
DBSCAN，全称为Density-Based Spatial Clustering of Applications with Noise，即"基于密度的带噪声空间聚类算法"。这个听起来有些复杂的名词其实蕴含着直观的理念：在数据空间中，同一个簇内的样本点应该具有相似的密度，而不同簇之间的区域密度相对较低，那些孤立的、密度异常低的点则被视为噪声。
这种基于密度的思想使得DBSCAN具有独特的优势：它不需要预先指定簇的个数，能够识别任意形状的簇，并且对噪声数据具有很好的鲁棒性。这些特性使得DBSCAN在实际应用中表现出色，特别是在处理复杂形状的数据集时。
DBSCAN的核心概念
要真正掌握DBSCAN，我们需要理解几个关键概念。首先是两个重要的参数：ε（eps）和MinPts。ε定义了邻域的半径大小，它决定了一个点的"影响力范围"；MinPts则定义了一个点成为核心点所需的最小邻域点数。这两个参数共同决定了算法对密度的敏感程度。
基于这两个参数，DBSCAN将数据点分为三种类型：核心点、边界点和噪声点。核心点是指在其ε邻域内至少包含MinPts个点的数据点，它们是簇形成的基础；边界点虽然自身的邻域内点数不足MinPts，但落在某个核心点的邻域内，因此被归入该核心点所在的簇；而那些既不是核心点也不是边界点的孤立点，则被标记为噪声点。
这种分类机制体现了DBSCAN的智慧：它不要求所有的点都满足核心点的条件，而是通过核心点来逐步"吸收"周围的边界点，从而形成完整的簇。这种机制也解释了为什么DBSCAN能够识别任意形状的簇------只要簇内的点密度相似且通过核心点相连，无论它们的空间分布是什么形状，都能被正确地识别为同一个簇。
在数据分析和机器学习领域，DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，它能够将具有足够高密度的区域划分为簇，并能很好地处理包含噪声和离群点的数据集。DBSCAN算法的核心思想是基于密度的概念，通过核心点、边界点和噪声点的划分来识别簇。
算法步骤
- 初始化：选择一个未访问的点作为起始点。
- 寻找核心点 ：以该点为中心，找出所有在其ε-邻域内的点。
- 如果找到的核心点数超过MinPts，则该点为核心点。
- 如果核心点的数量小于MinPts，但至少有一个核心点在其邻域内，则为边界点。
- 扩展簇 ：
- 从核心点开始，访问所有在其ε-邻域内的未访问点，并将它们加入当前簇。
- 重复此过程，直到没有更多的点可以加入当前簇。
- 继续搜索：继续从所有未访问的点中寻找新的核心点，重复步骤2和3，直到所有点都被访问过。
DBSCAN工作流程
DBSCAN的工作流程可以概括为以下几个步骤：算法首先随机选择一个未被访问的点，然后找出其ε邻域内的所有点。如果邻域内的点数达到或超过MinPts，就创建一个新簇，并将该点标记为核心点。接着，算法会递归地访问所有邻域内的点，不断扩展这个簇的范围。如果某个点的邻域内点数少于MinPts，它可能被暂时标记为噪声，但后续如果被发现落在其他核心点的邻域内，它仍然会被重新分类为边界点。这个过程重复进行，直到所有的点都被访问过。
这种基于密度可达性的扩展机制，使得DBSCAN能够自然地处理各种复杂情况。例如，它可以很好地处理簇与簇之间密度不同的情况，只要每个簇内部的密度相对均匀即可。同时，由于噪声点不会被任何核心点所"触及"，它们能够被有效地识别和隔离。
DBSCAN算法的伪代码：
# DB为数据集，distFunc为样本间的距离函数 # eps为样本点的领域，MinPts为簇类的最小样本数 DBSCAN(DB,distFunc,eps,minPts){ C = 0 # 初始化簇类个数 # 数据集DB被标记为核心点和噪声点 for each point P in database DB{ # 遍历数据集 if label(P) != undefined then continue # 如果样本已经被标记了，跳过此次循环 Neighbors N = RangeQuery(DB,distFunc,P,eps) # 计算样本点P在eps邻域内的个数，包含样本点本身 if |N| < minPts then { # 密度估计 label(P) = Noise # 若样本点P的eps邻域内个数小于MinPts，则为噪声 continue } C = C + 1 # 增加簇类个数 label(P) = C # 初始化簇类标记 Seed set S = N \{P} # 初始化种子集，符号\表示取补集 for each point Q in S{ if label(Q) = Noise then label(Q) = C # 核心点P的邻域为噪声点，则该噪声点重新标记为边界点 if label(Q) != undefined then continue # 如果样本已经被标记了(如上次已经被标记的噪声)，跳过此次循环 label(Q) = C # 核心点P的邻域都标记为簇类C Neighbors N = RangeQuery(DB,distFunc,Q,eps) # 计算样本Q的邻域个数 if N >= minPts then{ # 密度检测，检测Q是否为核心样本 S = S.append(N) # 邻域Q样本添加到种子集 } } } }
其中计算样本Q邻域个数的伪代码：
# 计算样本Q的eps邻域集 RangeQuery(DB,distFunc,Q,eps){ Neighbors = empty list # 初始化Q样本的邻域为空集 for each point P in database DB{ if distFunc(Q,P) <= eps then { Neighbors = Neighbors.append(Q) # 若Q在P的eps邻域内，则邻域集增加该样本 } } return Neighbors }
其中计算样本P与Q的距离函数dist(P,Q)不同，邻域形状也不同，若我们使用的距离是曼哈顿（manhattan）距离，则邻域性状为矩形；若使用的距离是欧拉距离，则邻域形状为圆形。
参数选择与优化策略
DBSCAN的性能在很大程度上依赖于参数的选择，特别是ε和MinPts的设定。如果ε选择得过小，可能会导致大量的点被错误地标记为噪声；而如果ε过大，则可能将本应分开的簇合并在一起。同样，MinPts的选择也需要谨慎：过小的MinPts会使算法对噪声过于敏感，而过大的MinPts则可能忽略一些有意义的较小簇。
在实际应用中，我们可以使用k-距离图来辅助选择ε参数。具体方法是计算每个点到其第k近邻的距离（通常k取MinPts），然后将这些距离按降序排列并绘制成图。图中的拐点通常对应着合适的ε值。对于MinPts的选择，一个常用的经验法则是将其设置为数据维度的两倍左右。
优缺点
优点：
1）DBSCAN不需要指定簇类的数量；
2）DBSCAN可以处理任意形状的簇类；
3）DBSCAN可以检测数据集的噪声，且对数据集中的异常点不敏感；
4）DBSCAN结果对数据集样本的随机抽样顺序不敏感（细心的读者会发现样本的顺序不一样，结果也可能不一样，如非核心点处于两个聚类的边界，若核心点抽样顺序不同，非核心点归于不同的簇类）；
缺点：
1）DBSCAN最常用的距离度量为欧式距离，对于高维数据集，会带来维度灾难，导致选择合适的值很难；
2）若不同簇类的样本集密度相差很大，则DBSCAN的聚类效果很差，因为这类数据集导致选择合适的minPts和值非常难，很难适用于所有簇类。
优缺点分析
任何算法都有其适用场景和局限性，DBSCAN也不例外。它的主要优点包括：不需要预先指定簇的数量、能够发现任意形状的簇、对噪声具有很好的鲁棒性、理论基础坚实等。这些优点使得DBSCAN在许多实际场景中都比传统的K-means表现更好。
然而，DBSCAN也存在一些明显的缺点。首先，它对参数的选择比较敏感，不同的参数设置可能导致完全不同的聚类结果。其次，在高维数据上，由于"维度灾难"的影响，DBSCAN的效果会大打折扣。此外，当数据集中不同簇的密度差异很大时，DBSCAN很难找到一个合适的参数设置来同时处理所有的簇。
代码实现
R语言
rm(list=ls())
# 生成数据
x1 <- seq(0,pi,length.out=100)
y1 <- sin(x1) + 0.1*rnorm(100)
x2 <- 1.5+ seq(0,pi,length.out=100)
y2 <- cos(x2) + 0.1*rnorm(100)
data <- data.frame(c(x1,x2),c(y1,y2))
names(data) <- c('x','y')
# 用K均值聚类
model1 <- kmeans(data,centers=2,nstart=10)
library(ggplot2)
p <- ggplot(data,aes(x,y))
p + geom_point(size=2.5,aes(colour=factor(model1$cluster)))
# 用fpc包中的dbscan函数进行密度聚类
library('fpc')
model2 <- dbscan(data,eps=0.6,MinPts=4)
p + geom_point(size=2.5, aes(colour=factor(model2$cluster)))python
在sklearn库中，DBSCAN类实现了DBSCAN聚类算法。以下是一些关键参数的简要介绍：
1. eps (float) : 表示邻域半径，即考虑一个点的邻域时的最大距离。这个参数定义了两点之间的最大距离，如果在这个距离内的点被认为是相互连接的。eps的选择对聚类结果有很大影响。
2. min_samples (int) : 表示一个点成为核心点所需的最小邻居数目，包括点本身。如果一个点的ε邻域内至少有min_samples个点，则该点被认为是核心点。这个参数与eps一起决定了聚类的形状和大小。
3. metric (string or callable) : 用于计算两点之间距离的度量方式。默认是'minkowski'（闵可夫斯基距离），但也可以是'euclidean'（欧几里得距离）、'manhattan'（曼哈顿距离）等，或者是一个自定义的距离度量函数。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans, DBSCAN
from sklearn import datasets
# 创建两个同心圆环数据
X, y = datasets.make_circles(n_samples=1000, noise=0.05, factor=0.5)
# 创建右上角的点簇
X1, y1 = datasets.make_blobs(n_samples=500, n_features=2, centers=[(1.5, 1.5)], cluster_std=0.2)
# 合并数据
X = np.concatenate((X, X1), axis=0)
y = np.concatenate((y, y1 + 2), axis=0)
# 使用Kmeans聚类
kMeans_instance = KMeans(n_clusters=3)
kMeans_instance.fit(X)
y_pred1 = kMeans_instance.predict(X)
# 使用DBSCAN聚类
DBSCAN_instance = DBSCAN(eps=0.2, min_samples=3)
DBSCAN_instance.fit(X)
y_pred2 = DBSCAN_instance.labels_
# 绘图部分
# 创建图像显示的子图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
ax1.scatter(X[:, 0], X[:, 1], c=y_pred1)
ax1.set_title('KMeans Result')
ax1.axis('off') # 不显示坐标轴
ax2.scatter(X[:, 0], X[:, 1], c=y_pred2)
ax2.set_title(f'DBSCAN Result')
ax2.axis('off') # 不显示坐标轴
plt.show()代码2
from sklearn.cluster import DBSCAN
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
def readFile(path):
df=pd.read_csv(path)
return df
if __name__=='__main__':
#读取数据
df=readFile('data.csv')
dataNd = df.values
print(dataNd)
print(type(dataNd))
DBSCANCluster = DBSCAN(eps=2, min_samples=4,metric='euclidean').fit(dataNd)#距离度量默认为euclidean
print(DBSCANCluster.labels_)
# 绘制图形
fig = plt.figure(1)
colors = ['r', 'g', 'y', 'b', 'r', 'c', 'g', 'b', 'k', 'm']
x = df.iloc[0:, 0].to_list()
print(x)
print(type(x))
y = df.iloc[0:, 1].to_list()
print(y)
area = 20 * np.arange(1, 10) # 设置点的面积大小 area 值
plt.scatter(x, y, alpha=0.5, marker='o')
plt.xlabel('X坐标')
plt.ylabel('Y坐标')
# 设置横轴的上下限值
plt.xlim(-5, 20)
# 设置纵轴的上下限值
plt.ylim(-5, 20)
# plt.savefig('test_xx.png', dpi=200, bbox_inches='tight', transparent=False)
plt.show()
# 绘制聚类后的图形
# 获取标签
label_DBSCAN = DBSCANCluster.labels_
set_label_DBSCAN=set(label_DBSCAN)
print(label_DBSCAN)
print(len(set_label_DBSCAN))
set_len=len(set_label_DBSCAN)#后面绘制图形时，不绘制离群数据点颜色
if -1 in label_DBSCAN:
set_len=set_len-1
color=['red','orange','blue','green','purple','cyan']
print(set_len)
for i in range(0,set_len):
print(i)
x0,y0= np.array(x)[label_DBSCAN == i], np.array(y)[label_DBSCAN == i]
plt.scatter(x0, y0, c=color[i], marker='o')
x0, y0 = np.array(x)[label_DBSCAN == -1], np.array(y)[label_DBSCAN == -1]
plt.scatter(x0, y0, alpha=0.5, marker='o')
# 获取数据值所在的范围
x_min, x_max = np.array(x).min() - 1, np.array(x).max() + 1
y_min, y_max = np.array(y).min() - 1, np.array(y).max() + 1
# 生成网格矩阵，半天未能运行出来，消耗较大内存
# xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.05), np.arange(y_min, y_max, 0.05))
# z = DBSCANCluster.fit_predict(np.c_[xx.ravel(), yy.ravel()])
# z = z.reshape(xx.shape)
# cs = plt.contourf(xx, yy, z)
plt.xlabel('X坐标')
# # 设置Y轴标签
plt.ylabel('Y坐标')
plt.xlim(-5, 20)
# 设置纵轴的上下限值
plt.ylim(-5, 20)
plt.show()MATLAB
function dbscan_demo()
% 生成示例数据
[X, y_true] = generate_sample_data();
% DBSCAN参数设置
eps = 0.25;
minPts = 8;
% 执行DBSCAN聚类
[labels, core_points] = my_dbscan(X, eps, minPts);
% 可视化结果
visualize_results(X, y_true, labels, core_points, eps, minPts);
end
function [X, y_true] = generate_sample_data()
% 生成包含三种不同形状簇和噪声的示例数据
rng(42); % 设置随机种子保证结果可重现
% 生成圆形簇
theta = linspace(0, 2*pi, 150)';
r = 1.5 + 0.15 * randn(150, 1);
cluster1 = [r .* cos(theta), r .* sin(theta)];
% 生成月牙形簇
theta2 = linspace(pi/4, 3*pi/4, 120)';
r2 = 2.5 + 0.25 * randn(120, 1);
cluster2 = [4 + r2 .* cos(theta2), 2 + r2 .* sin(theta2)];
% 生成线性簇
x3 = linspace(-3, 3, 100)';
y3 = 1.5*x3 + 2 + 0.2 * randn(100, 1);
cluster3 = [x3, y3];
% 生成随机噪声点
noise = 6 * rand(50, 2) - 3;
% 合并所有数据
X = [cluster1; cluster2; cluster3; noise];
y_true = [ones(150,1); 2*ones(120,1); 3*ones(100,1); 4*ones(50,1)];
% 随机打乱数据顺序
idx = randperm(size(X, 1));
X = X(idx, :);
y_true = y_true(idx);
end
function [labels, core_points] = my_dbscan(X, eps, minPts)
n = size(X, 1);
labels = zeros(n, 1); % 初始化标签数组，0表示未访问
cluster_id = 0; % 簇计数器
core_points = false(n, 1); % 核心点标记数组
% 计算距离矩阵
fprintf('正在计算距离矩阵...\n');
D = pdist2(X, X);
% 遍历所有数据点
for i = 1:n
if labels(i) ~= 0 % 跳过已访问的点
continue;
end
% 寻找当前点的ε邻域内的所有点
neighbors = find(D(i, :) <= eps);
% 判断是否为噪声点
if length(neighbors) < minPts
labels(i) = -1; % -1表示噪声点
continue;
end
% 创建新簇
cluster_id = cluster_id + 1;
labels(i) = cluster_id;
core_points(i) = true; % 标记为核心点
% 扩展簇：遍历当前点的所有邻域点
k = 1;
while k <= length(neighbors)
j = neighbors(k);
if labels(j) == -1 % 将噪声点重新分类为边界点
labels(j) = cluster_id;
elseif labels(j) == 0 % 处理未访问的点
labels(j) = cluster_id;
% 检查该点是否为核心点
j_neighbors = find(D(j, :) <= eps);
if length(j_neighbors) >= minPts
core_points(j) = true;
% 将新的邻域点加入待处理列表
neighbors = [neighbors, setdiff(j_neighbors, neighbors)];
end
end
k = k + 1;
end
end
% 输出聚类结果统计信息
fprintf('聚类完成！共发现 %d 个簇\n', cluster_id);
fprintf('核心点数量: %d, 噪声点数量: %d\n', sum(core_points), sum(labels == -1));
end
function visualize_results(X, y_true, labels, core_points, eps, minPts)
% 创建可视化窗口
figure('Position', [100, 100, 1500, 500]);
% 子图1：显示原始数据的真实分布
subplot(1, 4, 1);
gscatter(X(:,1), X(:,2), y_true, [0.2 0.6 0.8; 0.8 0.4 0.2; 0.4 0.8 0.2; 0.5 0.5 0.5], '.', 25);
title('(a) 原始数据分布', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('特征 X1');
ylabel('特征 X2');
axis equal;
grid on;
set(gca, 'FontSize', 11);
legend({'圆形簇', '月牙形簇', '线性簇', '噪声点'}, 'Location', 'best');
% 子图2：显示DBSCAN聚类结果
subplot(1, 4, 2);
% 定义更鲜明的颜色
colors = [
0.2 0.6 0.8; % 蓝色
0.8 0.4 0.2; % 橙色
0.4 0.8 0.2; % 绿色
0.8 0.2 0.6; % 粉色
0.6 0.4 0.8; % 紫色
0.8 0.8 0.2 % 黄色
];
hold on;
% 绘制各个簇
unique_labels = unique(labels);
for i = 1:length(unique_labels)
if unique_labels(i) == -1
continue; % 噪声点在下一个子图中单独显示
else
idx = labels == unique_labels(i);
color_idx = mod(i-1, size(colors, 1)) + 1;
scatter(X(idx, 1), X(idx, 2), 45, colors(color_idx, :), 'filled', ...
'MarkerEdgeColor', 'k', 'LineWidth', 0.5);
end
end
% 突出显示核心点
scatter(X(core_points, 1), X(core_points, 2), 100, 'ro', 'LineWidth', 2.5, ...
'MarkerFaceColor', 'none');
title('(b) DBSCAN聚类结果', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('特征 X1');
ylabel('特征 X2');
axis equal;
grid on;
set(gca, 'FontSize', 11);
legend('簇1', '簇2', '簇3', '核心点', 'Location', 'best');
hold off;
% 子图3：噪声点分析
subplot(1, 4, 3);
hold on;
% 绘制所有非噪声点
non_noise_idx = labels ~= -1;
scatter(X(non_noise_idx, 1), X(non_noise_idx, 2), 40, [0.7 0.7 0.7], 'filled');
% 突出显示噪声点
noise_idx = labels == -1;
scatter(X(noise_idx, 1), X(noise_idx, 2), 60, 'r', 'x', 'LineWidth', 2);
title('(c) 噪声点识别', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('特征 X1');
ylabel('特征 X2');
axis equal;
grid on;
set(gca, 'FontSize', 11);
legend('正常点', '噪声点', 'Location', 'best');
hold off;
% 子图4：邻域可视化
subplot(1, 4, 4);
plot_neighborhood(X, labels, core_points, eps);
end
function plot_neighborhood(X, labels, core_points, eps)
% 选择几个有代表性的核心点
core_indices = find(core_points);
if length(core_indices) > 4
% 选择分布在不同区域的核心点
distances = pdist2(X(core_indices, :), mean(X));
[~, sorted_idx] = sort(distances);
sample_cores = core_indices(sorted_idx(1:4:end));
if length(sample_cores) > 3
sample_cores = sample_cores(1:3);
end
else
sample_cores = core_indices;
end
colors = [
0.2 0.6 0.8; % 蓝色
0.8 0.4 0.2; % 橙色
0.4 0.8 0.2; % 绿色
];
hold on;
% 绘制所有数据点，按簇着色
unique_labels = unique(labels(labels ~= -1));
for i = 1:length(unique_labels)
idx = labels == unique_labels(i);
color_idx = mod(i-1, size(colors, 1)) + 1;
scatter(X(idx, 1), X(idx, 2), 35, colors(color_idx, :), 'filled', ...
'MarkerEdgeColor', 'k', 'LineWidth', 0.3);
end
% 绘制噪声点
scatter(X(labels == -1, 1), X(labels == -1, 2), 35, [0.5 0.5 0.5], 'x', 'LineWidth', 1);
% 绘制选定核心点的ε邻域范围
for i = 1:length(sample_cores)
idx = sample_cores(i);
% 绘制邻域圆
theta = linspace(0, 2*pi, 100);
x_circle = X(idx, 1) + eps * cos(theta);
y_circle = X(idx, 2) + eps * sin(theta);
fill(x_circle, y_circle, [1 0.8 0.8], 'EdgeColor', 'r', 'LineWidth', 2, 'FaceAlpha', 0.3);
% 标记核心点位置
plot(X(idx, 1), X(idx, 2), 'ro', 'MarkerSize', 10, 'LineWidth', 3, ...
'MarkerFaceColor', 'r');
end
title('(d) 核心点邻域分析', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('特征 X1');
ylabel('特征 X2');
axis equal;
grid on;
set(gca, 'FontSize', 11);
legend('簇1', '簇2', '簇3', '噪声点', 'ε邻域', '核心点', 'Location', 'best');
hold off;
end
% 运行演示程序
dbscan_demo();