一、阶跃函数
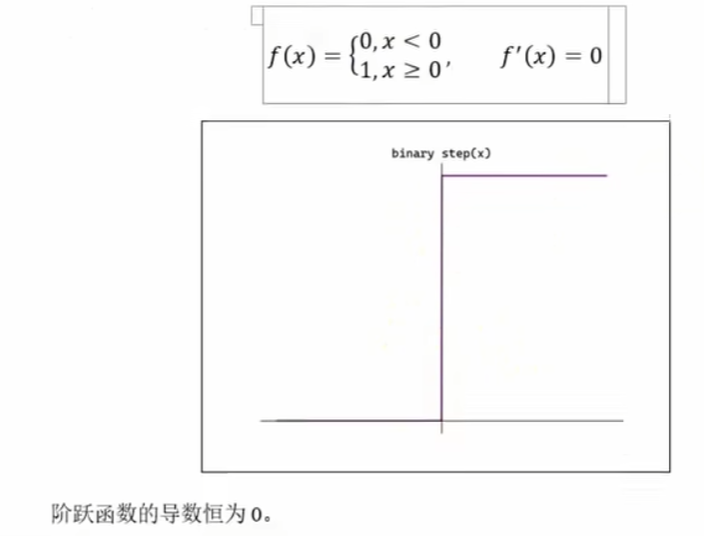
python
复制代码
import numpy as np
# 阶跃函数
def binary_step0(x):
if x>0:
return 1
return 0
# 阶跃函数-numpy
def binary_step(x):
return np.array(x > 0,dtype=int)
二、Sigmoid函数
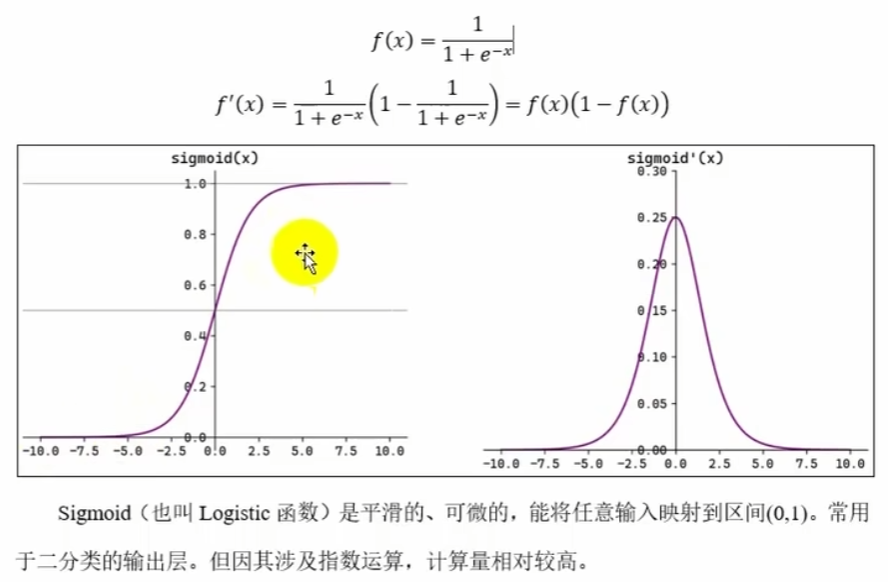

python
复制代码
import numpy as np
# Sigmoid函数
def sigmoid(x):
return 1/(1+np.exp(-x))
三、Tanh函数
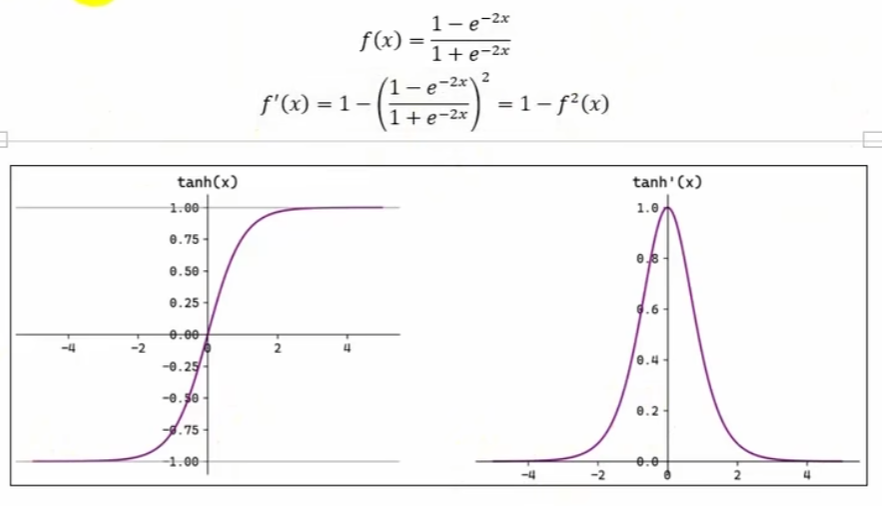

python
复制代码
import numpy as np
# Tanh函数
def tanh(x):
return np.tanh(x)
四、ReLu函数
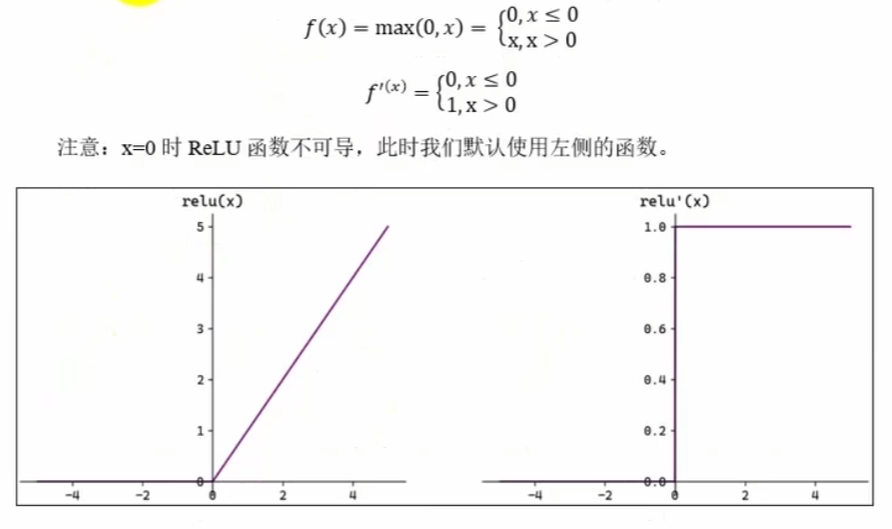

python
复制代码
import numpy as np
# ReLu函数
def relu(x):
return np.maximum(0,x)
# leaky ReLu函数
def leaky_relu(x,alpha=0.01):
return np.maximum(alpha*x,x)
# pReLu 函数(alpha 可训练) RReLu(alpha 在训练时在一个均匀分布中随机选取)
def pReLu(x,alpha):
return np.maximum(alpha*x,x)
# ELu
def EReLu(x,alpha):
return np.maximum(alpha*(np.exp(x)-1),x)
五、softmax函数

python
复制代码
import numpy as np
# softmax 函数
def softmax(x):
# 二维
if x.ndim==2:
# 溢出处理 keepdims保持维度一致
x=x-np.max(x,axis=1,keepdims=True)
# 二维axis有0 1 0表示高维 1表示次维 [高维][次维] 因为对行求 那么就是次维发生变化即 axis=1
return np.exp(x)/np.sum(np.exp(x),axis=1,keepdims=True)
# 三维
if x.ndim==3:
# 对行操作 则变化最低维 对列求操作变化最高维
return np.exp(x)/np.sum(np.exp(x),axis=2,keepdims=True)
# 一维的axis只有0
# 溢出处理
x=x-np.max(x)
return np.exp(x) / np.sum(np.exp(x), axis=0)
六、其他激活函数
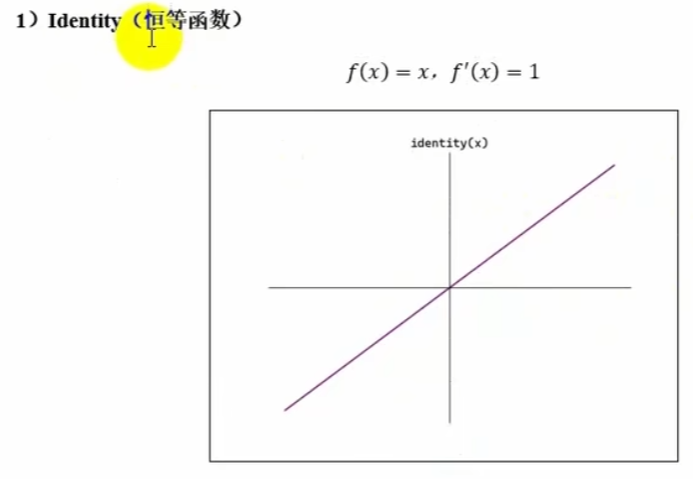
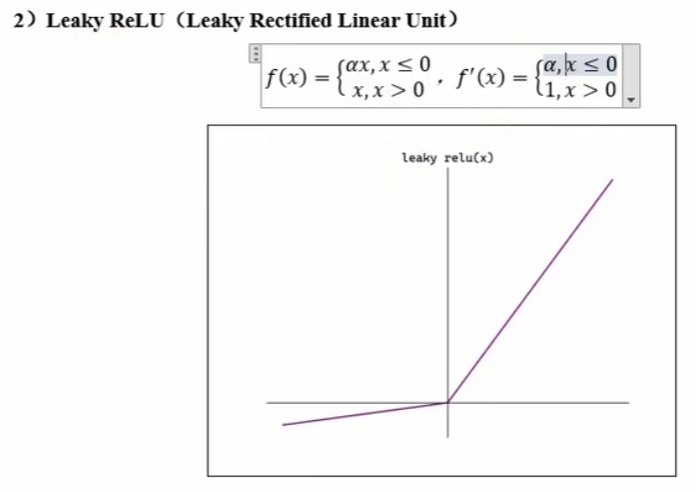
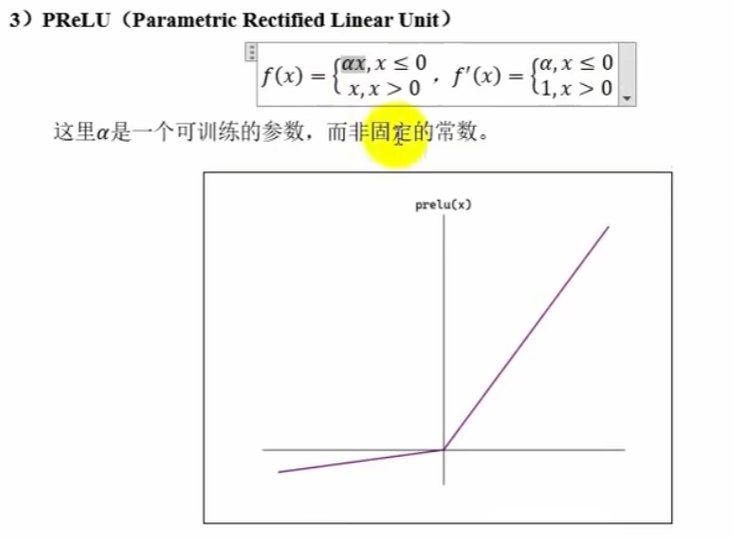
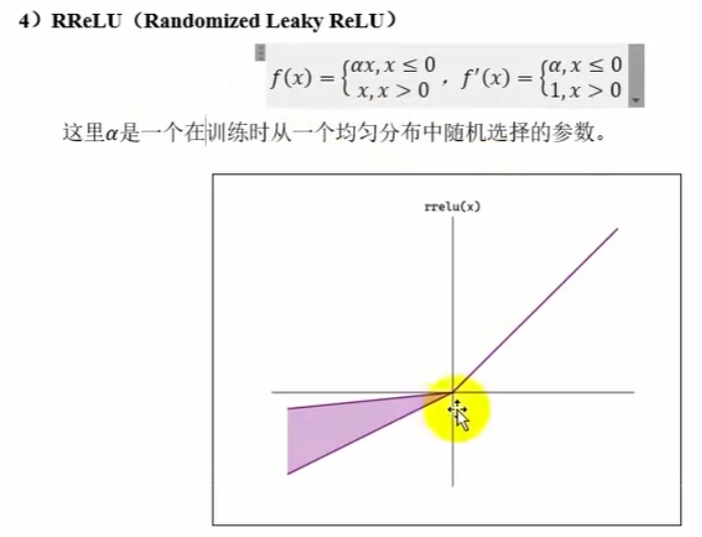
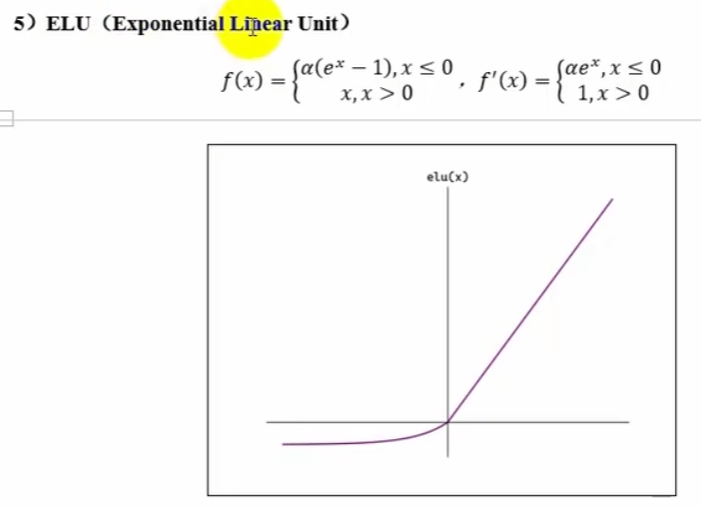
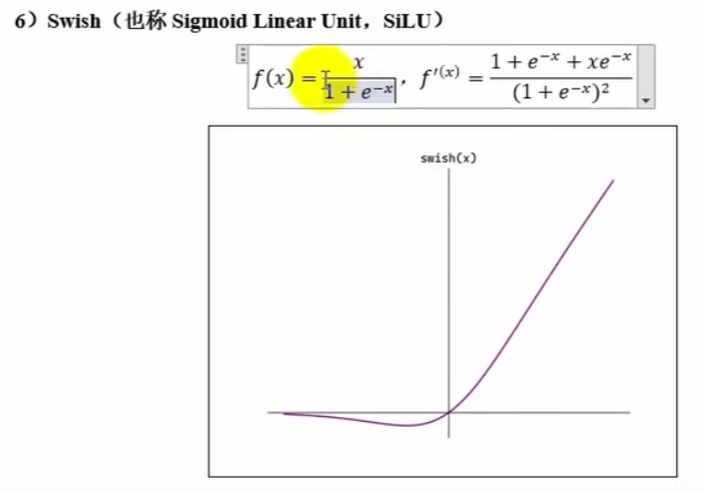
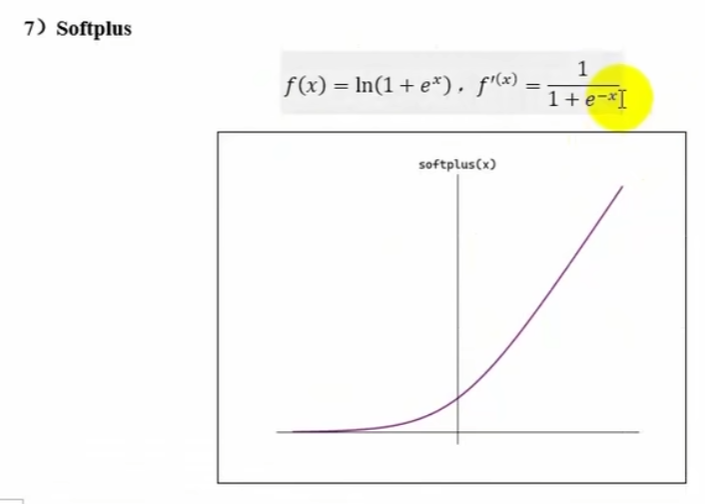
七、激活函数的选择
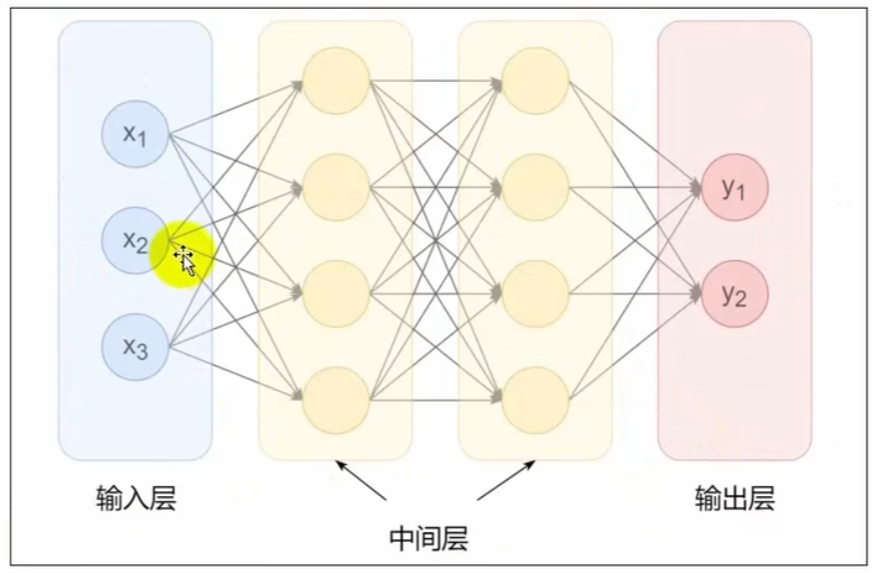

八、整体代码
python
复制代码
import numpy as np
# 阶跃函数
def binary_step0(x):
if x>0:
return 1
return 0
# 阶跃函数-numpy
def binary_step(x):
return np.array(x > 0,dtype=int)
# Sigmoid函数
def sigmoid(x):
return 1/(1+np.exp(-x))
# Tanh函数
def tanh(x):
return np.tanh(x)
# ReLu函数
def relu(x):
return np.maximum(0,x)
# leaky ReLu函数
def leaky_relu(x,alpha=0.01):
return np.maximum(alpha*x,x)
# pReLu 函数(alpha 可训练) RReLu(alpha 在训练时在一个均匀分布中随机选取)
def pReLu(x,alpha):
return np.maximum(alpha*x,x)
# ELu
def EReLu(x,alpha):
return np.maximum(alpha*(np.exp(x)-1),x)
# Swish (SiLu)
def Swish(x):
return x/1+(np.exp(-x))
# softmax 函数
def softmax(x):
# 二维
if x.ndim==2:
# 溢出处理 keepdims保持维度一致
x=x-np.max(x,axis=1,keepdims=True)
# 二维axis有0 1 0表示高维 1表示次维 [高维][次维] 因为对行求 那么就是次维发生变化即 axis=1
return np.exp(x)/np.sum(np.exp(x),axis=1,keepdims=True)
# 三维
if x.ndim==3:
# 对行操作 则变化最低维 对列求操作变化最高维
return np.exp(x)/np.sum(np.exp(x),axis=2,keepdims=True)
# 一维的axis只有0
# 溢出处理
x=x-np.max(x)
return np.exp(x) / np.sum(np.exp(x), axis=0)
# softplus
def softplus(x):
return np.log(1+np.exp(x))
# 恒等函数
def identity(x):
return x
if __name__ == '__main__':
arr=np.array([1,2,3,4,5,-1,-2,-3,-4,-5])
print(binary_step(arr))
print(sigmoid(arr))
print(tanh(arr))
print(relu(arr))
print(softmax(arr))
X = np.array([[1,2,3,4,5],[-1,-2,-3,-4,-5]])
print(softmax(X))
















