线性代数 - 奇异值分解（SVD Singular Value Decomposition）- 奇异值在哪里

flyfish

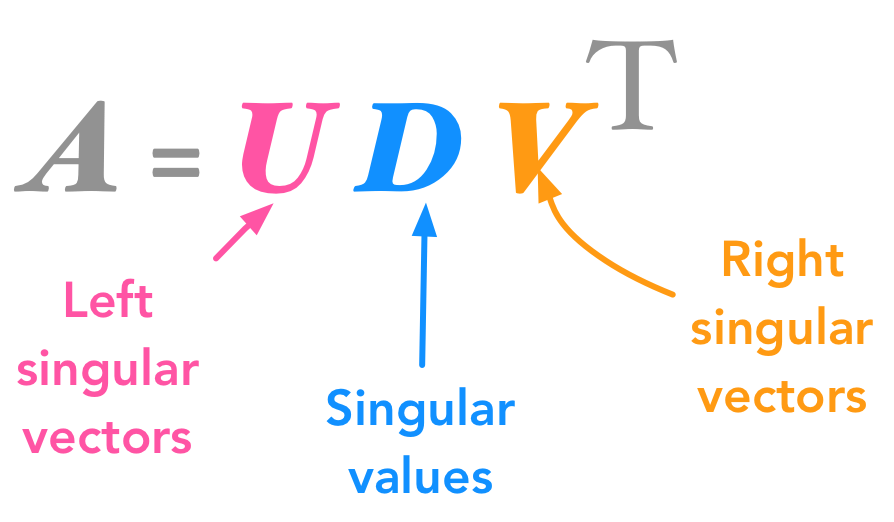
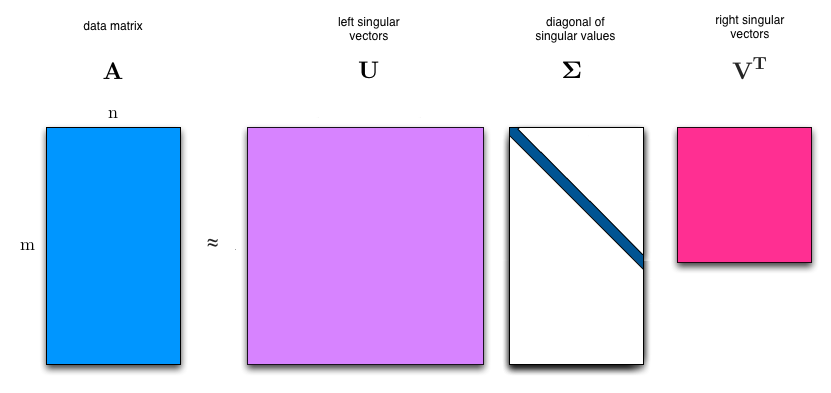
通过图中可以看到奇异值（singular balues）在D里面

公式： A = U Σ V T \mathbf{A} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T A=UΣVT

A \mathbf{A} A 是任意矩阵（可以是方阵、非方阵，比如2×3、3×4等）；
U \mathbf{U} U 和 V \mathbf{V} V 是正交矩阵 （满足 U T U = I \mathbf{U}^T \mathbf{U} = \mathbf{I} UTU=I、 V T V = I \mathbf{V}^T \mathbf{V} = \mathbf{I} VTV=I）；
Σ \mathbf{\Sigma} Σ是对角矩阵 ，对角线上的元素就是奇异值，按从大到小排列。

例如，一个3×3的对角矩阵形式为：
D = $d 1 0 0 0 d 2 0 0 0 d 3$ \mathbf{D} = \begin{bmatrix} d_1 & 0 & 0 \\ 0 & d_2 & 0 \\ 0 & 0 & d_3 \end{bmatrix} D= d1000d2000d3

其中 d 1 , d 2 , d 3 d_1, d_2, d_3 d1,d2,d3 是主对角线上的元素，其余位置（如 ( 1 , 2 ) (1,2) (1,2)、 ( 2 , 3 ) (2,3) (2,3)等）均为0。

对角矩阵是一类特殊的方阵（行数=列数），其特征是：仅主对角线（从左上角到右下角）上的元素可以非零，其余位置的元素全为0。

在奇异值分解 A = U Σ V T \mathbf{A} = \mathbf{U} \boxed{\mathbf{\Sigma}} \mathbf{V}^T A=UΣVT 中：

只有拉伸部分 Σ \boxed{\mathbf{\Sigma}} Σ 包含奇异值（即其对角线上的数值），这些值量化了矩阵在对应方向上的"拉伸强度"；

对角矩阵的符号

用希腊字母Σ（Sigma）的加粗形式，即 Σ {\mathbf{\Sigma}} Σ，英文读作 "sigma matrix"；
也常用大写字母D ，即 D \mathbf{D} D，英文读作 "D matrix"。

singular 的意思

日常（形容词）

单独的、单个的 （强调"数量唯一"） a singular example → 一个单独的例子、singular focus → 唯一的焦点
奇特的、特殊的 （强调"不寻常、与众不同"，略带中性或轻微褒义）：a singular style → 奇特的风格、singular talent → 非凡的天赋
单数（的）

Singular Form → 单数形式、Singular Number → 单数

对应"Plural（复数）"，是语法术语固定译法。

线性代数（场景）

奇异

Singular Matrix → 奇异矩阵（不可逆矩阵）、Singular Value → 奇异值

这里的"奇异"和日常含义无关

奇异向量和奇异值的载体

左奇异向量（Left singular vectors） ：指矩阵 U \mathbf{U} U 的列向量 ，这些列向量是 A A T \mathbf{A}\mathbf{A}^T AAT 的特征向量，组成的矩阵 U \mathbf{U} U 是正交矩阵（实现"旋转"操作）。

右奇异向量（Right singular vectors） ：指矩阵 V \mathbf{V} V 的列向量 ，这些列向量是 A T A \mathbf{A}^T\mathbf{A} ATA 的特征向量，组成的矩阵 V \mathbf{V} V 是正交矩阵（实现"旋转"操作）。

奇异值（Singular values） ：指对角矩阵 D \mathbf{D} D（图中用 D \mathbf{D} D 标注，也常用 Σ \mathbf{\Sigma} Σ）主对角线上的数值 ，是 A T A \mathbf{A}^T\mathbf{A} ATA（或 A A T \mathbf{A}\mathbf{A}^T AAT）特征值的非负平方根，实现"拉伸"操作。

U \mathbf{U} U 和 V \mathbf{V} V 是由奇异向量"组成的矩阵" （每个列向量是奇异向量）；
D \mathbf{D} D 是装奇异值的"对角矩阵"（数值本身是奇异值）。