一、什么是斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列 ,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称"兔子数列"
其数值为:0、1、1、2、3、5、8、13、21、34......
在数学上,这一数列以如下递推的方法定义:
F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)
二、基础题型
1.题目
现在有如下山寨版斐波拉契数列公式:
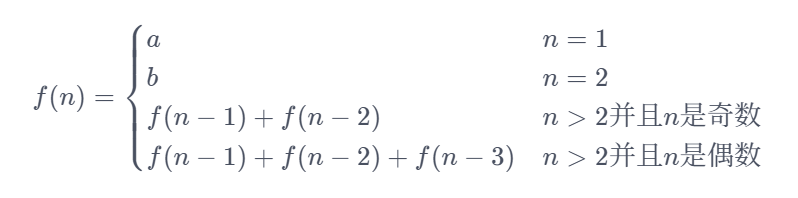
这里a和b是定值,现给出a,b和n,计算 f(n)。
++要求:++ 输入第一行有一个正整数T(T<=10),表示测试实例的个数。
每个测试实例一行,包括三个正整数a,b和n(a<=10,b<=10,n<=30)
输出对于每个测试实例,输出一行包含一个正整数f(n)。
2.题解
首先定义一个返回值为整型的函数fn用于处理数据
包含变量a,b,n
主函数输出
3.完整代码
cs
#include<stdio.h>
int fn(int a,int b,int n){
if(n==1){
return a;
}else if(n==2){
return b;
}else if(n>2&&n%2==0){
return fn(a,b,n-1)+fn(a,b,n-2)+fn(a,b,n-3);
}else{
return fn(a,b,n-1)+fn(a,b,n-2);
}
}
int main(){
int T;
scanf("%d",&T);
for(int i=0;i<T;i++){
int a,b,n;
int f=0;
scanf("%d %d %d",&a,&b,&n);
int N=fn(a,b,n);
printf("%d\n",N);
}
return 0;
}三、拓展题型
1.题目
现在,有一个新的斐波那契数列,定义如下:
F(0)=7,
F(1)=11,
F(n)=F(n−1)+F(n−2)(n>=2)
++要求:++输入包含多组测试样例,每组测试样例包含一个整数n (n<1,000,000)。
如果F(n)能够被3整除,请输出"yes",否则请输出"no"。
2.题解
按照常规思路来说,我们会按以下方式来写
cs
#include<stdio.h>
int fn(int n){
if(n==0){
return 7;
}else if(n==1){
return 11;
}else{
return fn(n-1)+fn(n-2);
}
}
int main(){
int n;
while(scanf("%d",&n)!=EOF){
if(fn(n)%3==0){
printf("yes\n");
}else{
printf("no\n");
}
}
return 0;
}这是最容易想到的的思路,也就是暴力枚举法,但是这样做的话运行时间会很长,远远超过了1s,效率很低,所以便需要转换思路来寻找一个效率相对较高的方法
处理超时问题最常用的思路就是找规律
目前我们已知该数列如下
1->7->1*7
2->11->1*11
3->18->1*7+1*11
4->29->1*7+2*11
5->...->2*7+3*11
6->...->3*7+4*11
7->...5*7+7*11
8->...8*7+11*11
......
到这里,我们发现每个数似乎都可以表示为a*7+b*11的形式(b>a)
要知道,题目要求找到能够整除三的数,而7+11=18刚好可以整除,所以我们只需找到(b-a)能够整除3的项即可
回过头来再看这个数列,我们不难发现一个规律:a和b似乎分别是一个斐波那契数列,二者刚好错位一个单位,所以可得出二者之差一定也是个斐波那契数列
回到数列当中,我们会发现两者之差从第四项开始是一个典型的斐波那契数列
通过观察斐波那契数列可得:其第4、8、12、16...项为三的倍数
故此题得解:n<=2时特殊考虑,>2时(n-2)%4==0则输出yes,否则输出no
3.完整代码
cs
#include<stdio.h>
int main(){
int n;
while(scanf("%d",&n)!=EOF){
if(n==0||n==1){
printf("no\n");
}else if(n==2){
printf("yes\n");
}else{
n-=2;
if(n%4==0){
printf("yes\n");
}else{
printf("no\n");
}
}
}
return 0;
}