数据结构：双向链表-从原理到实战完整指南

时间醉酒2025-11-07 18:56

引言:

在上期接触了链式存储结构并深入理解了单链表后，我们体会到了其动态灵活的特性。然而，单链表在某些查找和删除操作上存在明显不足：当需要访问节点的前驱时，我们往往需要从头开始遍历，效率低下。

为了克服这一痛点，本期我们将聚焦于双向链表。双向链表最大的特点在于，每个节点除了指向后继节点外，还新增了一个指向前驱节点的指针。这种设计赋予了我们在链表中"前后兼顾"的能力，极大地提升了操作的灵活性和效率，尤其是在需要回溯查找时。

接下来的内容，我们将通过代码实践，深入领会双向链表的结构、插入、删除、查找等核心操作，并对比其与单链表的异同，清晰展现双向链表如何成为单链表不可或缺的升级。将这个引言改的简短精炼一点

双向链表

基础结构定义:

cpp 复制代码 
#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;

//结构体定义
typedef struct node {
	ElemType data;
	struct node* prev; // 指向前一个节点
	struct node* next; // 指向下一个节点
}Node;

初始化:

cpp 复制代码 
//初始化
Node* initList()
{
	Node* head = (Node*)malloc(sizeof(Node));
	head->data = 0;
	head->next = NULL;
	return head;
}

遍历:

cpp 复制代码 
//遍历
void listNode(Node* L)
{
	Node* p = L->next;
	while (p != NULL)
	{
		printf("%d ", p->data);
		p = p->next;
	}
    printf("\n");
 }

双向链表-头插法

图解表示：

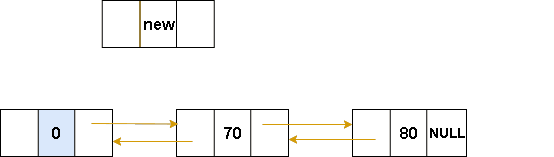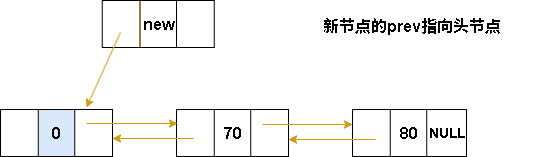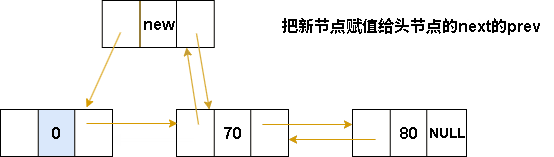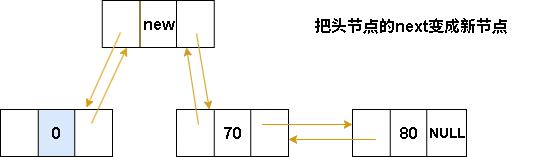
代码表示：

双向链表-头插法核心代码：

cs 复制代码 
//头插法
int insertHead(Node* L, ElemType e)
// L: 指向链表的头节点
// e: 要插入的数据
{
	Node* p = (Node*)malloc(sizeof(Node));
	
	//初始化新节点
	p->data = e;
	// 将新节点 p 的 prev 指向头节点 L
	p->prev = L;
	//头节点的next指向新节点的next
	p->next = L->next;
	if (L->next != NULL)
	{
	//新节点指向(赋值给)头节点的next的prev
		L->next->prev = p;
	}
    //新节点指向(赋值给)头节点的next
	L->next = p;
	return 1;

}

mian中调用

cpp 复制代码 
//初始化
Node* initList()
{
	Node* head = (Node*)malloc(sizeof(Node));
	head->data = 0;
	head->next = NULL;
	return head;
}

结果如下:

双向链表-尾插法

图解表示：

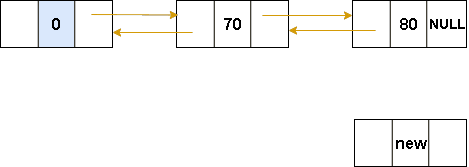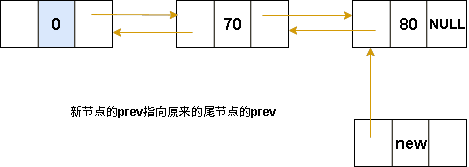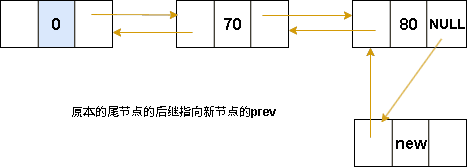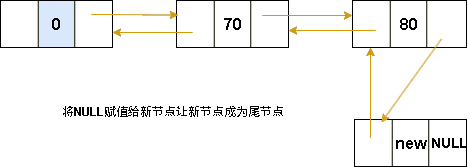
代码表示:

获取链表的尾节点

cpp 复制代码 
// 获取链表的尾节点（最后一个实际存储数据的节点）
Node* get_tail(Node* L) {
	if (L == NULL || L->next == NULL) {
		// 链表为空或只有一个头节点
		return L; // 返回头节点，插入尾部时会处理
	}
	Node* current = L;
	while (current->next != NULL) {
		current = current->next;
	}
	return current; // current 现在指向最后一个实际节点
}

双向链表-尾插法核心代码:

cpp 复制代码 
//尾插法
Node* insertTail(Node* tail, ElemType e)
{
	Node* p = (Node*)malloc(sizeof(Node));
	p->data = e;
	p->prev = tail;
	tail->next = p;
	p->next = NULL;
	return p;
}

在main中调用:

cs 复制代码 
int main(int argc, char const* argv[])
{
	Node* list = initList();

	Node* tail = get_tail(list);
	tail = insertTail(tail, 10);
	tail = insertTail(tail, 20);
	tail = insertTail(tail, 30);
	listNode(list);

}

结果如下:

双向链表-在指定位置插入数据

图解表示:

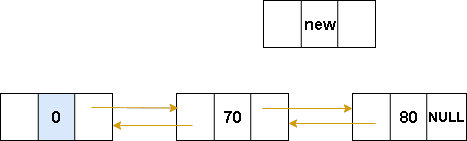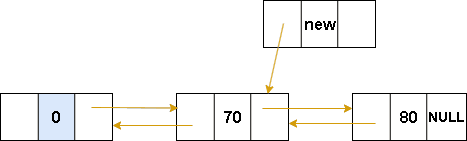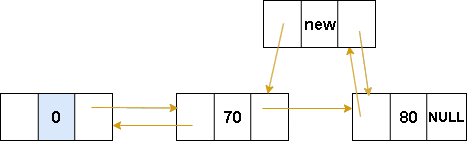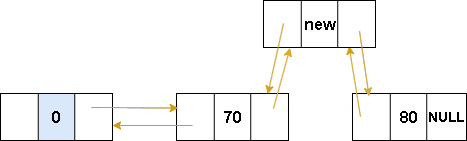
代码表示:

双向链表-中间插入核心代码

cs 复制代码 
//指定位置插入
int insertNode(Node* L, int pos, ElemType e)
{
	Node* p = L;
	int i = 0;
	while (i < pos - 1)
	{
		p = p->next;
		i++;
		if (p == NULL)
		{
			return 0;
		}
	}
	Node* q = (Node*)malloc(sizeof(Node));
	q->data = e;
	q->prev = p;
	q->next = p->next;
	p->next->prev = q;
	p->next = q;
	return 1;
}

在main中调用:

cs 复制代码 
int main(int argc, char const* argv[])
{
	Node* list = initList();

	Node* tail = get_tail(list);
	tail = insertTail(tail, 10);
	tail = insertTail(tail, 20);
	tail = insertTail(tail, 30);

	insertNode(list, 2, 15);
	listNode(list);
}

结果如下:

双向链表-删除节点

步骤如下:

1.找到要删除节点的前置节点p

2.用指针q记录要删除的节点

3.通过改变p的后继节及要删除节点的下一个节点的前驱实现删除

4.释放删除节点的空间

图解表示:

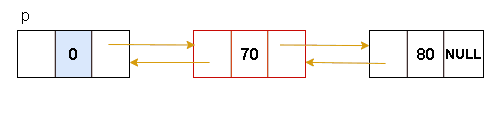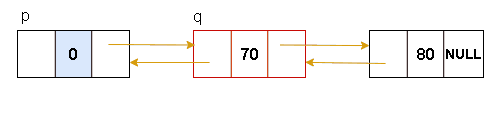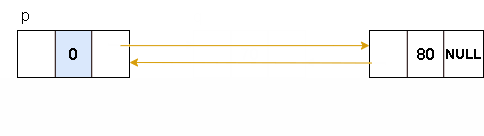
代码表示:

双链表删除节点核心代码:

cpp 复制代码 
//删除节点
int deleteNode(Node* L, int pos)
{
	Node* p = L;
	int i = 0;
	while (i < pos - 1)
	{
		p = p->next;
		i++;
		if (p == NULL)
		{
			return 0;
		}
	}
	Node* q = p->next;
	p->next = q->next;
	q->next->prev = p;
	free(q);
	return 1;
}

在main中调用:

cpp 复制代码 
int main(int argc, char const* argv[])
{
	Node* list = initList();

	//insertHead(list, 10);
	//insertHead(list, 20);
	//insertHead(list, 30);
	//listNode(list);

	Node* tail = get_tail(list);
	tail = insertTail(tail, 10);
	tail = insertTail(tail, 20);
	tail = insertTail(tail, 30);
	//listNode(list);

	insertNode(list, 2, 15);
	listNode(list);

	deleteNode(list,2);
	listNode(list);

}

结果如下:

释放双向链表

cpp 复制代码 
//释放链表
void freeList(Node* L)
{
	Node* p = L->next;
	Node* q;

	while (p != NULL)
	{
		q = p->next;
		free(p);
		p = q; 
	}
	L->next = NULL;
}

完整代码

cpp 复制代码 
#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;

//结构体定义
typedef struct node {
	ElemType data;
	struct node* prev; // 指向前一个节点
	struct node* next; // 指向下一个节点
}Node;

//初始化
Node* initList()
{
	Node* head = (Node*)malloc(sizeof(Node));
	head->data = 0;
	head->next = NULL;
	return head;
}

//头插法
int insertHead(Node* L, ElemType e)
// L: 指向链表的头节点
// e: 要插入的数据
{
	Node* p = (Node*)malloc(sizeof(Node));
	
	//初始化新节点
	p->data = e;
	// 将新节点 p 的 prev 指向头节点 L
	p->prev = L;
	//头节点的next指向新节点的next
	p->next = L->next;
	if (L->next != NULL)
	{
	//新节点指向(赋值给)头节点的next的prev
		L->next->prev = p;
	}
	L->next = p;
	return 1;
}

// 获取链表的尾节点（最后一个实际存储数据的节点）
Node* get_tail(Node* L) {
	if (L == NULL || L->next == NULL) {
		// 链表为空或只有一个头节点
		return L; // 返回头节点，插入尾部时会处理
	}
	Node* current = L;
	while (current->next != NULL) {
		current = current->next;
	}
	return current; // current 现在指向最后一个实际节点
}

//尾插法
Node* insertTail(Node* tail, ElemType e)
{
	Node* p = (Node*)malloc(sizeof(Node));
	p->data = e;
	p->prev = tail;
	tail->next = p;
	p->next = NULL;
	return p;
}

//指定位置插入
int insertNode(Node* L, int pos, ElemType e)
{
	Node* p = L;
	int i = 0;
	while (i < pos - 1)
	{
		p = p->next;
		i++;
		if (p == NULL)
		{
			return 0;
		}
	}
	Node* q = (Node*)malloc(sizeof(Node));
	q->data = e;
	q->prev = p;
	q->next = p->next;
	p->next->prev = q;
	p->next = q;
	return 1;
}

//删除节点
int deleteNode(Node* L, int pos)
{
	Node* p = L;
	int i = 0;
	while (i < pos - 1)
	{
		p = p->next;
		i++;
		if (p == NULL)
		{
			return 0;
		}
	}
	Node* q = p->next;
	p->next = q->next;
	q->next->prev = p;
	free(q);
	return 1;
}


//遍历
void listNode(Node* L)
{
	Node* p = L->next;
	while (p != NULL)
	{
		printf("%d ", p->data);
		p = p->next;
	}
	printf("\n");
 }

//释放链表
void freeList(Node* L)
{
	Node* p = L->next;
	Node* q;

	while (p != NULL)
	{
		q = p->next;
		free(p);
		p = q; 
	}
	L->next = NULL;
}

int main(int argc, char const* argv[])
{
	Node* list = initList();

	insertHead(list, 10);
	insertHead(list, 20);
	insertHead(list, 30);
	listNode(list);

	Node* tail = get_tail(list);
	tail = insertTail(tail, 10);
	tail = insertTail(tail, 20);
	tail = insertTail(tail, 30);
	//listNode(list);

	insertNode(list, 2, 15);
	listNode(list);

	deleteNode(list,2);
	listNode(list);

}

双向链表 vs. 单链表：异同对比表

特性/操作 单链表 (Singly Linked List) 双向链表 (Doubly Linked List) 主要差异
节点结构 data (数据域) + next (后继指针) data (数据域) + next (后继指针) + prev (前驱指针) 双向链表增加前驱指针
存储空间 每个节点比双向链表节点占用空间更少 每个节点比单链表节点占用空间更多 双向链表额外开销
遍历方向 只能从头节点向前遍历 可以 从头节点向前遍历，也可以从尾节点向后遍历 遍历方向的灵活性
查找前驱节点 效率低：需要从头节点开始遍历 效率高 ：通过 prev 指针可直接访问前驱节点 访问前驱的便捷性
删除节点 效率受限：若已知待删除节点，仍需查找其前驱才能完成删除；若只知道值，则需要两次遍历（一次找前驱，一次找节点） 效率高 ：若已知待删除节点，直接利用 prev 和 next 指针完成删除，无需查找前驱 删除操作的便捷性
插入节点 在已知节点的前/后插入，或在头/尾插入，操作相似 在已知节点的前/后插入，或在头/尾插入，操作相似 操作复杂度相似
实现复杂度 相对简单 相对复杂，需要维护 prev 指针的正确性 双向链表实现难度稍高
应用场景 简单的列表、栈、队列等，对前驱访问需求不高 需要频繁进行双向查找、查找前驱、或在任意位置高效删除的场景，如浏览器历史记录、LRU 缓存等 对访问方向的需求
  • 最大的区别在于节点结构 ：双向链表增加了 prev 指针，使其能够双向访问。
  • 主要优势体现在访问前驱和删除操作：双向链表在这两方面都比单链表更高效和便捷。
  • 代价是更高的空间开销和稍高的实现复杂度。

性能对比分析

操作类型 单链表 双向链表 性能提升
查找前驱 O(n) O(1) 显著
删除已知节点 O(n) O(1) 显著
插入到已知节点前 O(n) O(1) 显著
反向遍历 不支持 O(n) 新增功能
空间占用 较小 增加约33% 代价

总结

双向链表通过增加前驱指针的代价，换来了在多个操作场景下的性能提升。特别适合需要频繁进行双向遍历、前驱访问和任意位置删除的场景。在实际应用中，应根据具体需求权衡空间与时间的取舍，选择最适合的链表结构。

双向链表的实现虽然比单链表复杂，但其提供的操作灵活性和性能优势，使其成为数据结构工具箱中不可或缺的重要组成部分。

相关推荐
京东零售技术2 小时前
当搜索遇见 AIGC：京东零售的“千人千面”素材生成实践
算法
好学且牛逼的马2 小时前
【HOT100｜1 LeetCode 1. 两数之和】
数据结构·算法·leetcode
奔跑吧邓邓子2 小时前
【C语言实战(75)】C语言内存探秘：泄漏检测与分析实战
linux·c语言·windows·内存·开发实战·泄露检测
Nebula_g2 小时前
C语言应用实例：斐波那契数列与其其他应用
c语言·开发语言·后端·学习·算法
不穿格子的程序员2 小时前
从零开始刷算法-单调栈-每日温度
算法·单调栈
麦烤楽鸡翅2 小时前
挡住洪水 (牛客)
java·数据结构·c++·python·算法·bfs·牛客
MicroTech20252 小时前
微算法科技（NASDAQ MLGO）采用动态层次管理和位置聚类技术，修改pBFT算法以提高私有区块链网络运行效率
科技·算法·聚类
~~李木子~~2 小时前
五子棋项目Alpha-Beta剪枝与MCTS+神经网络实现人机对弈算法对比报告
神经网络·算法·剪枝
bigdata-rookie2 小时前
JVM 垃圾收集器介绍
java·jvm·算法
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06npm使用国内淘宝镜像的方法07《大数据技术原理与应用》实验报告三 熟悉HBase常用操作08BongoCat - 跨平台键盘猫动画工具09NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南10GitLab 零基础入门指南：从安装到项目管理全流程