ID3算法原理
ID3算法是一种用于构建决策树的经典算法。它的核心逻辑是根据 "信息增益" 来选择划分特征 ,通过递归的方式一步步构建决策树。简而言之,就是每次选择对分类结果最有帮助的特征 来分割数据,不断重复这个过程,直到生成一棵能对数据进行分类的决策树。 1. 特征选择
特征选择指的是从数据的多个特征中,挑选出最适合作为当前节点划分标准的那个特征。
- 熵
熵 是信息理论中用来衡量系统不确定性 的概念。在决策树等机器学习算法中,熵常常被用来作为划分数据集的指标,以便选择最优的划分方式。在这种情况下,熵可以用来衡量数据集的不确定性,以便选择能够降低不确定性的划分方式。
熵表示事物的混乱程度,熵越大表示混乱程度越大,越小表示混乱程度越小。对于随机事件S,如果我们知道它有N种取值情况,每种情况发生的概论为,那么这件事的熵就定义为:
 其中是分类出现的概率,是分类的数目。熵的大小只和变量的概率分布有关。
其中是分类出现的概率,是分类的数目。熵的大小只和变量的概率分布有关。
- 条件熵
条件熵 用于描述在已知一个随机变量X的条件下,另一个随机变量Y的不确定性(信息量)大小。
在给定X的每个可能取值 (Xi) 的条件下,Y的熵的加权平均 ,权重为X取 (Xi) 的概率 (P(Xi))。公式表示为
:
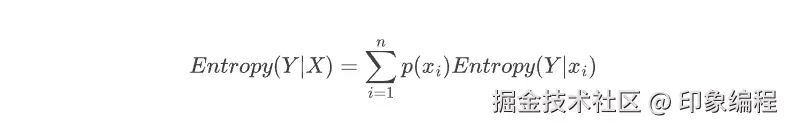 当
当Entropy最大为1的时候,是分类效果最差的状态,当它最小为0的时候,是完全分类的状态。因为熵等于零是理想状态,一般实际情况下,熵介于0和1之间
- 信息增益
信息增益是决策树算法中用来选择最佳划分属性的一个重要指标。在ID3算法中,期望通过选择最佳划分属性来构建决策树,对数据集进行最优的划分。
信息增益是定义 是数据集的原始信息熵 与给定特征条件下的条件熵 之差。计算每个特征值划分数据集获得的信息增益,获得信息增益最高的特征就是最好的选择。
信息增益计算的公式是:

算法流程

实验实现
1.实验目的
掌握ID3算法的原理,使用Python实现决策树ID3算法.
2.数据准备
数据要求:
下表显示了各种天气、温度、湿度和风速的场合下,是否进行打垒球的情况。
| 天气 | 温度 | 湿度 | 风速 | 活动 |
|---|---|---|---|---|
| 晴 | 炎热 | 高 | 弱 | 取消 |
| 晴 | 炎热 | 高 | 强 | 取消 |
| 阴 | 炎热 | 高 | 弱 | 进行 |
| 雨 | 适中 | 高 | 弱 | 进行 |
| 雨 | 寒冷 | 正常 | 弱 | 进行 |
| 雨 | 寒冷 | 正常 | 强 | 取消 |
| 阴 | 寒冷 | 正常 | 强 | 进行 |
| 晴 | 适中 | 高 | 弱 | 取消 |
| 晴 | 寒冷 | 正常 | 弱 | 进行 |
| 雨 | 适中 | 正常 | 弱 | 进行 |
| 晴 | 适中 | 正常 | 强 | 进行 |
| 阴 | 适中 | 高 | 强 | 进行 |
| 阴 | 炎热 | 正常 | 弱 | 进行 |
| 雨 | 适中 | 高 | 强 | 取消 |
转换为数据集 :保存为weather.csv,保存路径在与实验代码同路径即可。
天气,温度,湿度,风速,活动
晴,炎热,高,弱,取消
晴,炎热,高,强,取消
阴,炎热,高,弱,进行
雨,适中,高,弱,进行
雨,寒冷,正常,弱,进行
雨,寒冷,正常,强,取消
阴,寒冷,正常,强,进行
晴,适中,高,弱,取消
晴,寒冷,正常,弱,进行
雨,适中,正常,弱,进行
晴,适中,正常,强,进行
阴,适中,高,强,进行
阴,炎热,正常,弱,进行
雨,适中,高,强,取消3.算法实现
①读入文件数据
ini
# 读入数据
def createDataSet(csv_path='weather.csv'):
dataSet = []
with open(csv_path, 'r', encoding='utf-8') as file:
reader = csv.reader(file)
headers = next(reader)
for row in reader:
if not any(row): continue
dataSet.append(row)
labels = headers[:-1]
return dataSet, labels②计算信息熵
计算的是当前节点的**信息熵 **,用于后续计算信息增益。
实现逻辑:统计数据集的总样本数,统计每个类别(目标变量)的出现次数,根据熵的公式计算数据集的不确定性。
ini
def calEnt(dataSet):
sampleCounts = len(dataSet)
labelCounts = {}
for sample in dataSet:
label = sample[-1]
labelCounts[label] = labelCounts.get(label, 0) + 1
Ent = 0.0
for k in labelCounts:
p = float(labelCounts[k]) / sampleCounts
Ent -= p * log(p, 2)
return Ent③划分数据集
实现逻辑:根据指定特征索引(index)和特征值(value),筛选出符合条件的样本;移除已用于划分的特征列,生成子数据集;返回子数据集(ret)。
ini
def splitDataSet(dataSet, index, value):
ret = []
for sample in dataSet:
if sample[index] == value:
reduced = sample[:index] + sample[index + 1:]
ret.append(reduced)
return ret④选择最优划分特征
ID3算法的核心,通过信息增益最大化选择当前节点的最优划分特征。
实现逻辑:计算数据集的原始信息熵 ;遍历所有特征,统计该特征的所有唯一取值,对每个取值,划分数据集并计算条件熵 ;计算信息增益,选择信息增益最大的特征索引并返回。
ini
def chooseBestFeatureToSplit(dataSet):
featureCounts = len(dataSet[0]) - 1
baseEnt = calEnt(dataSet)
bestGain = 0.0
bestIndex = -1
for i in range(featureCounts):
vals = [s[i] for s in dataSet]
unique = set(vals)
newEnt = 0.0
for v in unique:
sub = splitDataSet(dataSet, i, v)
prob = len(sub) / float(len(dataSet))
newEnt += prob * calEnt(sub)
gain = baseEnt - newEnt
if gain > bestGain:
bestGain = gain
bestIndex = i
return bestIndex⑤处理叶节点
当数据集无法再划分(无特征可用或所有样本类别相同)时,通过多数投票确定叶节点的类别。
实现逻辑:统计标签列表中每个类别出现的次数;按次数降序排序,返回出现次数最多的类别。
ini
def majorLabel(labels):
counts = {}
for l in labels:
counts[l] = counts.get(l, 0) + 1
sorted_counts = sorted(counts.items(), key=lambda x: x[1], reverse=True)
return sorted_counts[0][0]⑥递归构建决策树
实现决策树的递归生长,从根节点到叶节点逐步构建完整的树结构。
ini
def createTree(dataSet, labels):
labelList = [s[-1] for s in dataSet]
if labelList.count(labelList[0]) == len(labelList):
return labelList[0]
if len(dataSet[0]) == 1:
return majorLabel(labelList)
best = chooseBestFeatureToSplit(dataSet)
bestFeat = labels[best]
tree = {bestFeat: {}}
subLabels = labels[:]
del subLabels[best]
featVals = [s[best] for s in dataSet]
uniqueVals = set(featVals)
for val in uniqueVals:
tree[bestFeat][val] = createTree(splitDataSet(dataSet, best, val), subLabels[:])
return tree⑦可视化
将构建好的决策树字典转换为直观的图形,便于可视化分析。
ini
def tree_to_graphviz(tree, graph_name='DecisionTree'):
dot = graphviz.Digraph(graph_name, format='png')
# 设置字体为支持中文的字体
dot.attr('node', fontsize='12', fontname='Microsoft YaHei', shape='box', style='filled', fillcolor='lightyellow')
# 使用自增 id(保证唯一,即使相同标签多次出现)
node_id_counter = {'n': 0}
def gen_id():
node_id_counter['n'] += 1
return f"n{node_id_counter['n']}"
def recurse(node, parent_id=None, edge_label=None):
if isinstance(node, dict):
feat = list(node.keys())[0]
node_id = gen_id()
# 节点的颜色、字体、边框设置
dot.node(node_id, label=str(feat), fillcolor='lightblue', style='filled', shape='ellipse',
fontname='Microsoft YaHei', fontsize='10', fontcolor='black')
if parent_id is not None:
dot.edge(parent_id, node_id, label=str(edge_label), fontname='Microsoft YaHei', fontsize='10',
fontcolor='black', color='gray')
# 遍历分支
for val, subtree in node[feat].items():
recurse(subtree, parent_id=node_id, edge_label=val)
else:
# 叶子节点设置
leaf_id = gen_id()
dot.node(leaf_id, label=str(node), shape='ellipse', style='filled', fillcolor='lightgray',
fontname='Microsoft YaHei', fontsize='10', fontcolor='black')
if parent_id is not None:
dot.edge(parent_id, leaf_id, label=str(edge_label), fontname='Microsoft YaHei', fontsize='10',
fontcolor='black', color='gray')
recurse(tree)
return dot4.实验结果

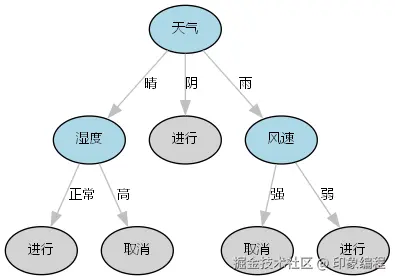
完整代码
ini
import csv
from math import log
import os
os.environ["PATH"] += os.pathsep + "D:\Graphviz\bin"
import graphviz
# 读入数据
def createDataSet(csv_path='weather.csv'):
dataSet = []
with open(csv_path, 'r', encoding='utf-8') as file:
reader = csv.reader(file)
headers = next(reader)
for row in reader:
if not any(row): continue
dataSet.append(row)
labels = headers[:-1]
return dataSet, labels
# 计算信息熵
def calEnt(dataSet):
sampleCounts = len(dataSet)
labelCounts = {}
for sample in dataSet:
label = sample[-1]
labelCounts[label] = labelCounts.get(label, 0) + 1
Ent = 0.0
for k in labelCounts:
p = float(labelCounts[k]) / sampleCounts
Ent -= p * log(p, 2)
return Ent
# 划分数据集
def splitDataSet(dataSet, index, value):
ret = []
for sample in dataSet:
if sample[index] == value:
reduced = sample[:index] + sample[index + 1:]
ret.append(reduced)
return ret
# 选择最优划分特征
def chooseBestFeatureToSplit(dataSet):
featureCounts = len(dataSet[0]) - 1
baseEnt = calEnt(dataSet)
bestGain = 0.0
bestIndex = -1
for i in range(featureCounts):
vals = [s[i] for s in dataSet]
unique = set(vals)
newEnt = 0.0
for v in unique:
sub = splitDataSet(dataSet, i, v)
prob = len(sub) / float(len(dataSet))
newEnt += prob * calEnt(sub)
gain = baseEnt - newEnt
if gain > bestGain:
bestGain = gain
bestIndex = i
return bestIndex
# 处理叶节点
def majorLabel(labels):
counts = {}
for l in labels:
counts[l] = counts.get(l, 0) + 1
sorted_counts = sorted(counts.items(), key=lambda x: x[1], reverse=True)
return sorted_counts[0][0]
# 递归构建决策树
def createTree(dataSet, labels):
labelList = [s[-1] for s in dataSet]
if labelList.count(labelList[0]) == len(labelList):
return labelList[0]
if len(dataSet[0]) == 1:
return majorLabel(labelList)
best = chooseBestFeatureToSplit(dataSet)
bestFeat = labels[best]
tree = {bestFeat: {}}
subLabels = labels[:]
del subLabels[best]
featVals = [s[best] for s in dataSet]
uniqueVals = set(featVals)
for val in uniqueVals:
tree[bestFeat][val] = createTree(splitDataSet(dataSet, best, val), subLabels[:])
return tree
# ---------------- 可视化部分 ----------------
def tree_to_graphviz(tree, graph_name='DecisionTree'):
dot = graphviz.Digraph(graph_name, format='png')
# 设置字体为支持中文的字体
dot.attr('node', fontsize='12', fontname='Microsoft YaHei', shape='box', style='filled', fillcolor='lightyellow')
# 使用自增 id(保证唯一,即使相同标签多次出现)
node_id_counter = {'n': 0}
def gen_id():
node_id_counter['n'] += 1
return f"n{node_id_counter['n']}"
def recurse(node, parent_id=None, edge_label=None):
if isinstance(node, dict):
feat = list(node.keys())[0]
node_id = gen_id()
# 节点的颜色、字体、边框设置
dot.node(node_id, label=str(feat), fillcolor='lightblue', style='filled', shape='ellipse',
fontname='Microsoft YaHei', fontsize='10', fontcolor='black')
if parent_id is not None:
dot.edge(parent_id, node_id, label=str(edge_label), fontname='Microsoft YaHei', fontsize='10',
fontcolor='black', color='gray')
# 遍历分支
for val, subtree in node[feat].items():
recurse(subtree, parent_id=node_id, edge_label=val)
else:
# 叶子节点设置
leaf_id = gen_id()
dot.node(leaf_id, label=str(node), shape='ellipse', style='filled', fillcolor='lightgray',
fontname='Microsoft YaHei', fontsize='10', fontcolor='black')
if parent_id is not None:
dot.edge(parent_id, leaf_id, label=str(edge_label), fontname='Microsoft YaHei', fontsize='10',
fontcolor='black', color='gray')
recurse(tree)
return dot
# ---------------- 主流程 ----------------
if __name__ == '__main__':
dataSet, labels = createDataSet('weather.csv') # 请确保同目录下有 weather.csv
labels_copy = labels[:]
tree = createTree(dataSet, labels_copy)
print("生成的决策树:\n", tree)
dot = tree_to_graphviz(tree, graph_name='WeatherDecisionTree')
# 保存 dot 文件
dot_filepath = 'decision_tree.gv'
dot.save(dot_filepath)
print(f"dot 文件已保存为: {dot_filepath}")
# 渲染为 png
out = dot.render(filename='decision_tree', cleanup=True) # 生成 decision_tree.png