零基础入门C语言之C语言实现数据结构之顺序表

在阅读本篇文章之前，希望读者优先阅读本专栏内前面的文章。

目录

前言

一、数据结构

二、顺序表

总结

---

前言

首先恭喜大家看完了我们前面关于C语言语法部分的文章，从本篇文章开始，我们就开始使用C语言来实现数据结构。本篇文章主要是用C语言实现数据结构中的顺序表。

---

一、数据结构

既然我们现在开始学习数据结构了，那么肯定首先就是要了解一下数据结构究竟是什么？顾名思义，数据结构是由数据和结构两部分组合而成的。那么什么是数据？常见的数值1、2、3......，教务系统里保存的用户信息（姓名、性别、年龄、学历等等）、网页里肉眼可以看到的信息（文字、图片、视频等等），这些都是数据。 什么是结构？ 当我们想要使用大量同一类型的数据时，手动定义大量独立变量会使程序可读性很差，我们可以借助数组等数据结构将大量数据组织在一起，结构可理解为组织数据的方式。 比如，想要找到草原上名叫"咩咩"的羊很难，但从羊圈里找1号羊就很简单，羊圈这样的结构有效将羊群组织起来。 所以**数据结构是计算机存储、组织数据的方式。**是指相互之间存在一种或多种特定关系的数据元素的集合。反映数据的内部构成，即数据由哪部分构成、以什么方式构成，以及数据元素之间呈现的结构。 总的来说，数据结构能够存储数据（如顺序表、链表等结构）并且存储的数据能够方便查找。

那我们为什么需要数据结构呢？如果我们现在在食堂打饭，不借助排队的方式来管理客户，会导致客户就餐感受差、等餐时间长、餐厅营业混乱等情况。同理，程序中如果不对数据进行管理，可能会导致数据丢失、操作数据困难、野指针等情况。通过数据结构，能够有效将数据组织和管理在一起，按照我们的方式任意对数据进行增删改查等操作。其中我们曾经学过的最基础的数据结构就是数组。既然有了数组，我们为什么还要学习其他的数据结构？假定数组有 10 个空间，已经使用了 5 个，向数组中插入数据步骤如下，求数组的长度，求数组的有效数据个数，向下标为数据有效个数的位置插入数据（注意：这里是否要判断数组是否满了，满了还能继续插入吗）......假设数据量非常庞大，频繁的获取数组有效数据个数会影响程序执行效率。所以我们得到一个结论，最基础的数据结构能够提供的操作已经不能完全满足复杂算法实现。

二、顺序表

我们首先来介绍一种简单的数据结构，顺序表。顺序表的本质其实就是数组，只不过它实现了对数组的封装和常用的增删查改等接口。顺序表是线性表的一种，这个线性表是n个具有相同特性的数据元素的有限序列。它是一种在实际中广泛使用的数据结构，常见的线性表有顺序表、链表、栈、队列、字符串等。之后的这些数据结构我们会在后面的文航进行讲解。

线性表在逻辑上是线性结构，即呈连续的直线型；但在物理结构上不一定连续，存储时通常以数组和链式结构的形式实现。如同蔬菜分为绿叶类、瓜类、菌菇类，线性表是具有部分相同特性的一类数据结构的集合。

那么我们在前面提到的这个物理结构和逻辑结构分别都是什么意思呢？逻辑结构指数据元素之间抽象的逻辑关系，是独立于计算机存储介质的 "理论关系"，描述的是数据元素 "如何关联"，不关心数据实际存在内存的哪个位置。比如排队的人群，逻辑上是 "前 - 后" 的线性顺序关系，这和人群是站在连续的走廊还是分散的大厅无关。物理结构又称存储结构，指数据元素及其逻辑关系在计算机物理内存中的具体存储方式，解决的是数据 "实际存在哪、怎么存" 的问题，直接影响数据操作的效率。比如同样是排队的人群信息，既可以存到连续的内存地址（类似数组），也可以存到分散地址且用指针关联（类似链表）。

我们的顺序表又可以分为静态顺序表和动态顺序表两种，其中静态顺序表指的是用定长数组存储元素，如下图所示：

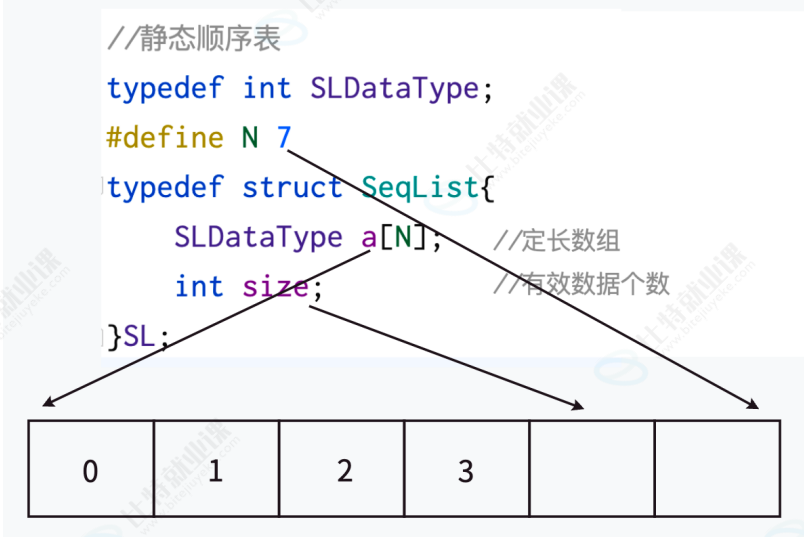
我们通过如下的方式实现静态顺序表：

struct SeqList
{
 int arr[100]; //定长数组
 int size; //空间大小
};

而动态顺序表则是通过动态内存分配函数来实现的，如下图所示：

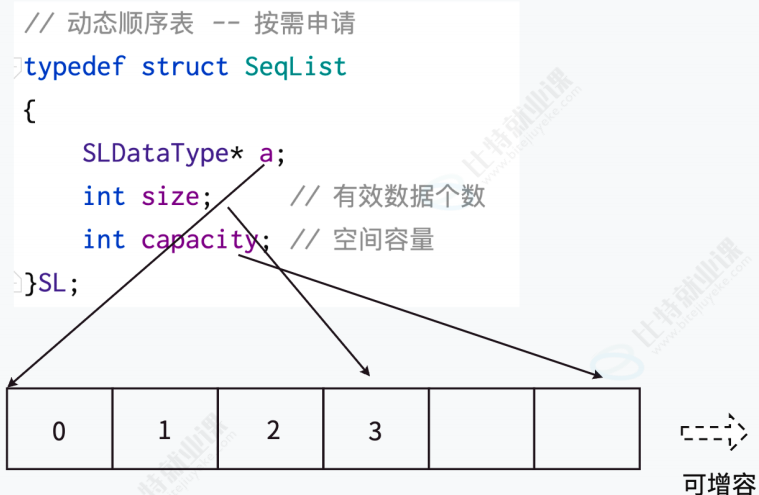
我们以如下的方式来实现动态顺序表：

struct SeqList
{
 int* arr;
 int size;//有效数据的个数
 int capacity;//空间大小
};

相比来说，哪一种是更好的方式呢？答案是动态顺序表，因为静态顺序表有着有一定的缺陷，就是如果空间过小，就不够我们的使用；而如果空间过大，就会造成浪费。而动态顺序表则是可以实现动态增容，使顺序表更为灵活。

由于我们的顺序表很有可能不只会存储整形类型，所以说为了方便，我们修改代码如下：

typedef int SLDataType;

//动态顺序表
typedef struct SeqList
{
	SLDataType* arr;
	int size;//有效数据的个数
	int capacity;//空间大小
}SL;

那么我们如果想要实现顺序表，肯定要先实现对其的初始化，这样才能够进行后续对其的操作，那么请读者思考一下我们该如何实现这个初始化函数呢？我给出示例代码如下：

void SLInit(SL* ps) {
	ps->arr = NULL;
	ps->capacity = 0;
	ps->size = 0;
}

可以看到经由调试之后，发现我们的这个sl顺序表成功完成了初始化：

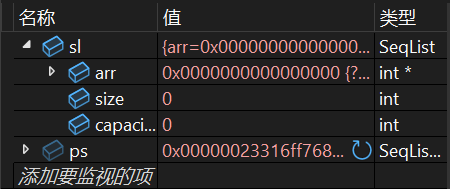
那么我们完成开始的创建，下一步就是去完成末尾的销毁动作，那么我们该如何去实现这个销毁动作呢？请读者先行思考一下，我给出示例代码如下：

void SLDestroy(SL* ps) {
	if (ps->arr) {
		free(ps->arr);
	}
	ps->arr = NULL;
	ps->capacity = 0;
	ps->size = 0;
}

这段代码我们不再进行调试证明。那么此时我们就已经完成了对于一个顺序表的起始和最终操作，接下来我们就可以完成其内部的增删查改等操作，首先我们先来实现尾部元素的增加和删除操作：

void SLPushBack(SL* ps, SLDataType x) {
	assert(ps);
	if (ps->size == ps->capacity) {
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		SLDataType* tmp = (SLDataType*)realloc(ps->arr,newCapacity * 2 * sizeof(SLDataType));
		if (tmp == NULL) {
			perror("realloc");
			exit(1);
		}
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
	ps->arr[ps->size++] = x;
}

 SLPushBack(&sl, 1);
 SLPushBack(&sl, 2);
 SLPushBack(&sl, 3);
 SLPushBack(&sl, 4);
 SLPushBack(&sl, 5);

其调试结果如下，可以看见我们的5个元素成功插入到顺序表中：

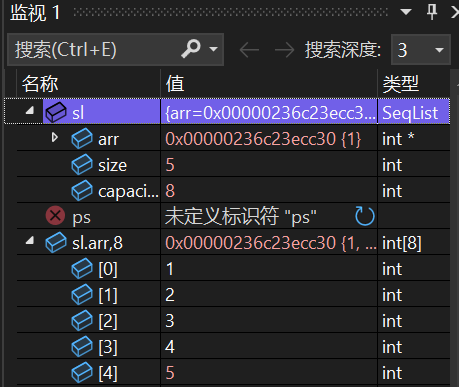
我们在增容的时候，通常会选择增加原来的整数倍，一般都是2倍。如果说我们给出一个确定的数字的话，它很难符合我们所有的需求，这就有可能导致我们需要频繁地增容，进而导致程序运行效率大大降低。

在掌握完上面的知识后，我们再来试着写一下顺序表的头部插入元素，但是在写之前，我们还是需要先思考一下，既然要插入元素，我们仍需要考虑空间的问题，而这个检测空间的方法和之前的尾插是一样的，所以我们可以想办法将其封装为一个函数，如下：

void SLCheckCapacity(SL* ps) {
	if (ps->size == ps->capacity) {
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		SLDataType* tmp = (SLDataType*)realloc(ps->arr, newCapacity * 2 * sizeof(SLDataType));
		if (tmp == NULL) {
			perror("realloc");
			exit(1);
		}
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
}

这样的话，我们的头插代码就十分好写了：

void SLPushFront(SL* ps, SLDataType x) {
	assert(ps);
	SLCheckCapacity(ps);
	for (int i = ps->size; i > 0; i--)
	{
		ps->arr[i] = ps->arr[i - 1];//arr[1] = arr[0]
	}
	ps->arr[0] = x;
	ps->size++;
}

SLPushFront(&sl, 0);
SLPushFront(&sl, -1);
SLPushFront(&sl, -2);
SLPushFront(&sl, -3);
SLPushFront(&sl, -4);

其运行结果如下：

如果说每回运行代码我们都要自己去进行调试监视，那就太麻烦了，所以说我们最好是写一个顺序表元素打印代码，方便我们观察结果：

void SLPrint(SL* ps) {
	assert(ps);
	for (int i = 0; i < ps->size; i++) {
		printf("%d ", ps->arr[i]);
	}
	printf("\n");
}

其运行结果如下：

接下来我们再来想一下如何实现尾部元素的删除，我给出我的示例代码：

void SLPopBack(SL* ps) {
	assert(ps);
	assert(ps->size);
	--ps->size;
}

可以看到，其实尾删的代码是十分简单的，我们只需要保证最后的有效元素个数减1就可以了。我们试着删除一下后面两个元素试试：

可以看到成功完成了删除，然后让我们再思考一下如何实现头部元素的删除，我给出我的示例代码：

void SLPopFront(SL* ps) {
	assert(ps);
	assert(ps->size);
	for (int i = 0; i < ps->size - 1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];
	}
	ps->size--;
}

我们的头删代码相对来说，也是比较简单的，我们可以通过直接元素覆盖来实现。我们用这段头删代码来实现删除两个元素试试：

发现我们已经成功实现了。但是我们很多时候根本不想一定要从顺序表的头部或尾部开始插入删除，而是在某一个特定位置之前插入或者删除，那我们该如何实现呢？我们首先先来思考一下插入的代码，我给出示例：

void SLInsert(SL* ps, int pos, SLDataType x) {
	assert(ps);
	assert(pos >= 0 && pos <= ps->size);
	SLCheckCapacity(ps);
	for (int i = ps->size; i > pos; i--)
	{
		ps->arr[i] = ps->arr[i - 1];
	}
	ps->arr[pos] = x;
	ps->size++;
}

我们在测试代码部分键入如下代码，看看是否插入成功：

void SLTest02() {
    SL sl;
    SLInit(&sl);
    SLPushBack(&sl, 1);
    SLPushBack(&sl, 2);
    SLPushBack(&sl, 3);
    SLPushBack(&sl, 4);
    SLPushBack(&sl, 5);
    SLPrint(&sl);

	SLInsert(&sl, 2, 100);
	SLPrint(&sl);
    SLInsert(&sl, 0, 200);
	SLPrint(&sl);
}

其运行结果如下：

可以看到运行成功，那么我们再来试一试指定位置的元素的删除，我给出如下示例：

void SLErase(SL* ps, int pos) {
	assert(ps);
	assert(pos >= 0 && pos < ps->size);
	for (int i = pos; i < ps->size - 1; i++) {
		ps->arr[i] = ps->arr[i + 1];
	}
	ps->size--;
}

我们把刚刚添加的两个元素进行删除，结果如下：

最后我们来实现一下寻找特定元素的位置，这个函数是很容易实现的，请读者思考，我这里给出示例代码：

int SLFind(SL* ps, SLDataType x) {
	assert(ps);
	for (int i = 0; i < ps->size; i++) {
		if (ps->arr[i] == x) {
			return i;
		}
	}
	return -1;
}

我们在测试代码中键入如下代码：

printf("%d\n", SLFind(&sl, 3));
printf("%d\n", SLFind(&sl, 100));

运行结果如下：

那么到这，我们关于顺序表这部分的知识就基本完成了。

---

总结

本文详细介绍了用C语言实现数据结构中的顺序表。顺序表本质是对数组的封装，分为静态和动态两种形式，其中动态顺序表通过内存分配更灵活。文章讲解了顺序表的初始化、销毁、增删查改等核心操作，包括尾插尾删、头插头删、指定位置插入删除等功能的实现。通过示例代码演示了动态扩容、元素查找等关键操作，并强调了数据结构在高效组织和管理数据方面的重要性。顺序表作为线性表的基础结构，为后续学习链表、栈等更复杂数据结构打下基础。