排序算法介绍

下面介绍排序算法的代码，代码示例都是从小到大排列，仅作为自己的记录。

下面代码中用到的swap函数

cpp 复制代码

void swap(int& first, int& second) {
	int temp = first;
	first = second;
	second = temp;
}

1.冒泡排序

冒泡排序的思想就是比较两个相邻元素，如果前一个元素比后一个元素大，那么就交换两个元素。

c++语言

cpp 复制代码

void bubbleSort(int arr[], int size) {
    if (arr == nullptr || size < 2)
		return;
	for (int i = 0; i < size - 1; ++i) {
        // 设置一个flag，如果遍历一次后，发现flag还是false，说明列表本来就有序
		bool flag = false;    
		for (int j = 0; j < size - 1 - i; ++j) {
			if (arr[j] > arr[j + 1]) {
				swap(arr[j], arr[j+1]);
				flag = true;
			}		
		}
		if (!flag) return;
	}
}

2.选择排序

选择排序的思想就是从数组中依次选择最小的一个，然后和第一个元素交换。

cpp 复制代码

void selectSort(int arr[], int size) {
    if (arr == nullptr || size < 2)
		return;
	for (int i = 0; i < size - 1; ++i) {
		int min = arr[i];
		for (int j = i + 1; j < size; ++j) {
			if (arr[j] < min)
				swap(arr[j], min);
		}
		if (min != arr[i])
			swap(arr[i], min);
	}
}

3.插入排序

插入排序的思想就是假定数组为有序的列表，然后将后面的元素依次插入到数组中。

cpp 复制代码

void insertSort(int arr[], int size) {
    if (arr == nullptr || size < 2)
		return;
	for (int i = 1; i < size; ++i) {
		int val = arr[i];
		int j = i - 1;
		for (; j >= 0; --j) {
			if (arr[j] <= val)
				break;
			arr[j + 1] = arr[j];
		}
		arr[j + 1] = val;
	}
}

解法2

cpp 复制代码

void insertSort2(int arr[], int size) {
	if (arr == nullptr || size < 2) {
		return;
	}
	for (int i = 1; i < size; ++i) {
		for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
			swap(arr[j], arr[j + 1]);
		}
	}
}

4.希尔排序

希尔排序就是在插入排序的基础上优化，按照分组的思想，将整体慢慢变得有序。

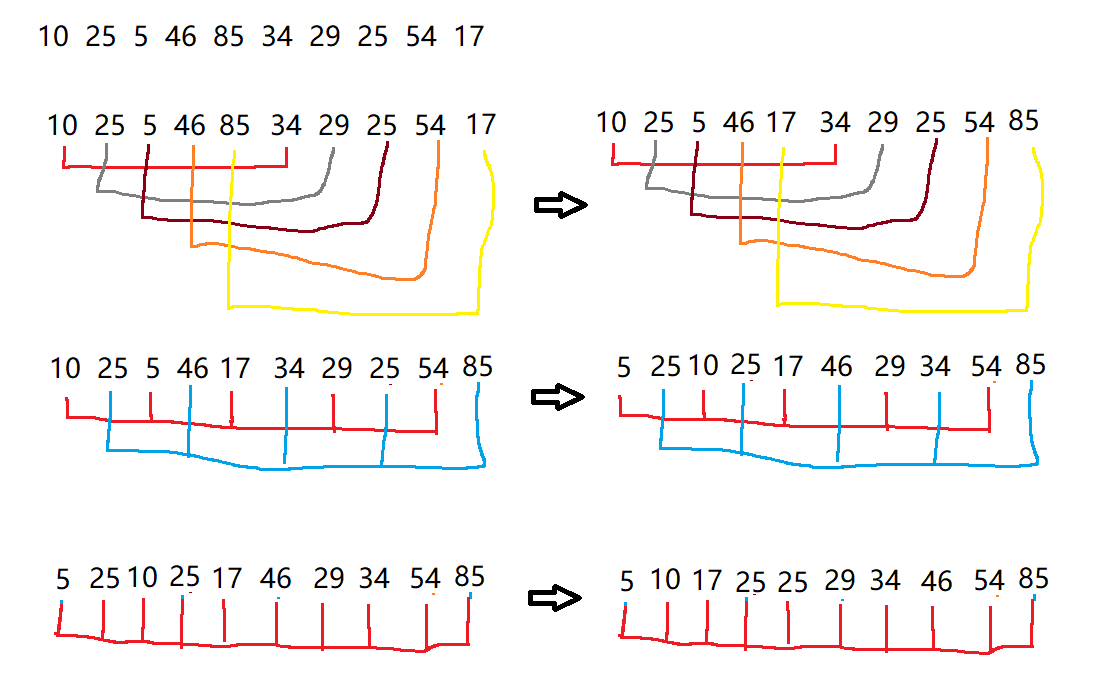
cpp 复制代码

void shellSort(int arr[], int size) {
	for (int gap = size / 2; gap > 0; gap /= 2) {
		for (int i = gap; i < size; ++i) {
			int val = arr[i];
			int j = i - gap;
			for (; j >= 0; j -= gap) {
				if (arr[j] <= val)
					break;
				arr[j + gap] = arr[j];
			}
			arr[j + gap] = val;
		}
	}
}

.5.快速排序

快速排序的思想

选择基准数，假设选取第一个元素val

2.从右边R开始往前找第一个 < val的数字，放到L的地方 L++；

3.从L开始往后找第一个 > val的数字，放到R的地方，R--；

4.重复上面的操作

cpp 复制代码

int partition(int arr[], int l, int r) {
	// 记录基准数
	int val = arr[l];
	// 依次快排处理
	while (l < r) {
		while (arr[r] > val && l < r)
			r--;
		if (l < r)
			arr[l++] = arr[r];
		while (arr[l] < val && l < r)
			l++;
		if (l < r)
			arr[r--] = arr[l];
	}
	arr[l] = val;
	return l;
}

void QuickSort(int arr[], int begin, int end) {
	// 快排递归的结束条件
	if (begin >= end)
		return;
	// 优化一：当[begin, end]序列的元素个数小到指定数量，采用插入排序
	// if (end - begin <= 50) {
		// insertSort(arr, begin, end);
		// return;
	}
	// 在[begin, end]区间的元素做一次快排分割处理
	int pos = partition(arr, begin, end);
	// 对基准数的左边和右边的序列，再分别进行快排
	QuickSort(arr, begin, pos - 1);
	QuickSort(arr, pos + 1, end);
}

void quickSort(int arr[], int size) {
	QuickSort(arr, 0, size - 1);
}

可以考虑优化的点有两个：

第一个是随着区间越来越小，数据越来越趋于有序，而当数据越来越趋于有序的时候，插入排序的效率就要比快排的效率高了；

第二个就是基准数的选择，最好的选择当然是恰好选取最中间的数，这样递归的深度就在logN了，采用"三数取中法"，找合适的基准数，找到最左边，最右边，中间的三个数，取数值在中间的数为基准数。