【算法基础篇】（四十四）数论之欧拉定理与扩展欧拉定理深度解析：从降幂到超大规模幂运算

---

目录

​编辑

前言

[一、欧拉定理回顾：费马小定理的 "泛化升级"](#一、欧拉定理回顾：费马小定理的 “泛化升级”)

[1.1 定理的核心表述](#1.1 定理的核心表述)

与费马小定理的关联

[1.2 定理的核心价值：欧拉降幂](#1.2 定理的核心价值：欧拉降幂)

降幂示例

[1.3 欧拉定理的局限性](#1.3 欧拉定理的局限性)

[二、扩展欧拉定理：无互质要求的 "终极降幂"](#二、扩展欧拉定理：无互质要求的 “终极降幂”)

[2.1 定理的完整表述](#2.1 定理的完整表述)

[2.2 定理的核心应用场景](#2.2 定理的核心应用场景)

三、核心工具：欧拉函数计算与快速幂实现

[3.1 试除法计算单个欧拉函数](#3.1 试除法计算单个欧拉函数)

[C++ 实现](#C++ 实现)

代码分析

[3.2 快速幂算法（含模运算）](#3.2 快速幂算法（含模运算）)

[C++ 实现](#C++ 实现)

代码分析

[四、实战例题 1：洛谷 P5091 【模板】扩展欧拉定理](#四、实战例题 1：洛谷 P5091 【模板】扩展欧拉定理)

[4.1 题目分析](#4.1 题目分析)

[4.2 解题思路](#4.2 解题思路)

[4.3 C++ 实现](#4.3 C++ 实现)

[五、实战例题 2：洛谷 P4139 上帝与集合的正确用法](#五、实战例题 2：洛谷 P4139 上帝与集合的正确用法)

[5.1 题目分析](#5.1 题目分析)

[5.2 解题思路](#5.2 解题思路)

[5.3 C++ 实现（预处理欧拉函数 + 递归）](#5.3 C++ 实现（预处理欧拉函数 + 递归）)

[C++ 实现](#C++ 实现)

[5.4 代码分析与优化](#5.4 代码分析与优化)

六、常见误区与避坑指南

[6.1 扩展欧拉定理的降幂规则记错](#6.1 扩展欧拉定理的降幂规则记错)

[6.2 欧拉函数计算错误](#6.2 欧拉函数计算错误)

[6.3 大指数处理时溢出](#6.3 大指数处理时溢出)

[6.4 忽略模数为 1 的特殊情况](#6.4 忽略模数为 1 的特殊情况)

[6.5 递归时未处理边界条件](#6.5 递归时未处理边界条件)

总结

---

前言

在算法竞赛的数论领域，处理大指数幂取模问题时，直接计算无疑是天方夜谭 ------ 比如计算 mod 1000000007，哪怕是超级计算机也无法直接完成。而欧拉定理与扩展欧拉定理，正是解决这类问题的 "降幂神器"。它们不仅是费马小定理的泛化延伸，更打破了模数和底数的限制，成为处理超大规模幂运算的核心工具。本文将从定理本质出发，层层拆解欧拉定理、扩展欧拉定理的原理与应用，结合经典例题，手把手教你掌握从理论到实战的全流程，让你在大指数幂问题中轻松破局。下面就让我们正式开始吧！

---

一、欧拉定理回顾：费马小定理的 "泛化升级"

1.1 定理的核心表述

欧拉定理（Euler's Theorem）指出：

若整数 a 与正整数 m 互质（即 gcd(a,m)=1），则有 。

其中 **φ(m)**是欧拉函数，表示 1 到 m 中与 m 互质的数的个数（前文已详细讲解欧拉函数的计算方法）。

与费马小定理的关联

当 m 为质数时，欧拉函数φ(m)=m−1（质数的欧拉函数性质），此时欧拉定理就退化为费马小定理：。可以说，费马小定理是欧拉定理的特殊情况，而欧拉定理是费马小定理的 "泛化升级"------ 它允许模数 m 为任意正整数，只需满足 a 与 m 互质即可。

1.2 定理的核心价值：欧拉降幂

欧拉定理的最大作用是 "降幂"------ 将指数通过欧拉函数缩小，从而简化大指数幂的计算。具体来说：对于，若 gcd(a,m)=1，则可将指数 b 对 φ(m) 取模，即：

这是因为，所以 （其中 r=b mod φ(m)）。

降幂示例

计算 3^{100} mod 4：

• gcd(3,4)=1，φ(4)=2；
• 指数降幂：100 mod 2 = 0；
• 因此 3^{100} ≡ 3^{0} = 1(mod 4)，与直接计算结果一致。

1.3 欧拉定理的局限性

欧拉定理虽然强大，但存在两个明显限制：

1. 要求 a 与 m 互质 ------ 若 gcd(a,m)>1，定理不成立；
2. 仅能处理指数降幂，无法覆盖所有大指数幂取模场景（如 a 与 m 不互质且指数极大的情况）。

而扩展欧拉定理的出现，正是为了打破这些限制，成为真正意义上的 "通用降幂工具"。

二、扩展欧拉定理：无互质要求的 "终极降幂"

2.1 定理的完整表述

**扩展欧拉定理（Extended Euler's Theorem）**取消了 "a 与 m 互质" 的要求，给出了更通用的降幂规则：对于任意整数 a、正整数 m 和非负整数 b，有：

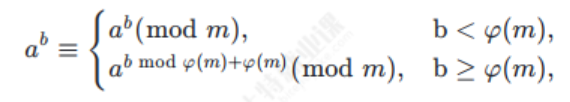
这个定理的核心突破在于：无论 a 与 m 是否互质，只要指数 b 足够大（b≥φ(m)），就可以通过**"b mod φ(m) + φ(m)"**进行降幂。额外加上 φ(m) 是为了避免 b mod φ(m) = 0 时出现 a^{0}=1 的错误。

2.2 定理的核心应用场景

扩展欧拉定理几乎覆盖了所有大指数幂取模场景，尤其适用于：

1. 指数极大的情况（如 b=1018）；
2. 底数与模数不互质的情况；
3. 模数为任意正整数的情况。

在算法竞赛中，这类场景常见于：

• 超级大指数幂取模（如模板题 "扩展欧拉定理"）；
• 递归定义的幂运算（如 "上帝与集合的正确用法"）；
• 组合数学中的高次幂计算（如含大指数的组合数取模）。

三、核心工具：欧拉函数计算与快速幂实现

要应用欧拉定理与扩展欧拉定理，必须掌握两个基础工具：欧拉函数的计算（单个数字）和快速幂算法（高效计算幂取模）。

3.1 试除法计算单个欧拉函数

根据欧拉函数的公式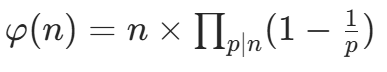（p 为 n 的质因子），我们可以用试除法高效计算单个数字的欧拉函数。

C++ 实现

#include <iostream>
using namespace std;

typedef long long LL;

// 试除法计算单个数字的欧拉函数
LL get_phi(LL x) {
    LL ret = x;
    // 枚举质因子，直到 sqrt(x)
    for (LL i = 2; i <= x / i; ++i) {
        if (x % i == 0) {
            // 应用公式：ret = ret * (i-1) / i
            ret = ret / i * (i - 1);
            // 除尽所有i的倍数，避免重复计算
            while (x % i == 0) {
                x /= i;
            }
        }
    }
    // 剩余x>1，说明是最后一个质因子
    if (x > 1) {
        ret = ret / x * (x - 1);
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    LL m;
    cin >> m;
    cout << "φ(" << m << ") = " << get_phi(m) << endl;
    return 0;
}

代码分析

• 时间复杂度：O(x​)，对于 x=1e12，x=1e6，完全可以毫秒级完成；
• 溢出处理：使用 long long 存储结果，"先除后乘"（如 ret = ret / i * (i-1)）确保中间结果为整数，避免小数误差。

3.2 快速幂算法（含模运算）

快速幂算法通过二进制分解指数，将时间复杂度从 O(b) 降至 O(logb)，是计算 a ^{b} mod m 的核心工具。

C++ 实现

#include <iostream>
using namespace std;

typedef long long LL;

// 快速幂计算 (a^b) mod p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    a = a % p;  // 先对底数取模，防止溢出
    while (b > 0) {
        // 若当前二进制位为1，将结果乘上当前底数的幂次
        if (b & 1) {
            ret = ret * a % p;  // 边乘边取模，避免溢出
        }
        // 底数平方，对应二进制位左移一位
        a = a * a % p;
        // 指数右移一位，处理下一个二进制位
        b >>= 1;
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    LL a = 2, b = 10, p = 4;
    cout << (a ^ b) << " mod " << p << " = " << qpow(a, b, p) << endl;
    return 0;
}

代码分析

• 时间复杂度：O(logb)，对于 b=1e18，log2b≈60，仅需 60 次循环；
• 溢出处理：每次乘法后都对 p 取模，确保中间结果始终在 p 范围内，避免大数相乘溢出。

四、实战例题 1：洛谷 P5091 【模板】扩展欧拉定理

题目链接：https://www.luogu.com.cn/problem/P5091

4.1 题目分析

题目描述：给定三个正整数 a、m、b（其中 b 可能极大，以字符串形式输入），求a^{b} mod m。

输入描述 ：一行三个整数 a、m、b（b 以字符串形式输入，长度可能达 1e6）。输出描述：一个整数，表示 abmodm 的结果。

示例输入 ：2 7 4 → 输出：2示例解析：24=16mod7=2，直接计算即可。

核心难点：

1. b 极大（长度达 1e6），无法直接存储为整数，需边读入边处理；
2. 需根据扩展欧拉定理判断指数 b 与 φ(m) 的大小关系，选择对应的降幂策略。

4.2 解题思路

1. 计算模数 m 的欧拉函数 φ(m)；
2. 处理指数 b：由于 b 以字符串形式输入，需边读入边计算 b mod φ(m)，同时记录 b 是否大于等于 φ(m)；
3. 根据扩展欧拉定理降幂：
   • 若 b<φ(m)，直接计算；
   • 若 b≥φ(m)，计算；
4. 注意：若 a=0 且 b=0，需特殊处理（本题 b 为正整数，可忽略）。

4.3 C++ 实现

#include <iostream>
#include <string>
using namespace std;

typedef long long LL;

// 试除法计算单个数字的欧拉函数
LL get_phi(LL x) {
    LL ret = x;
    for (LL i = 2; i <= x / i; ++i) {
        if (x % i == 0) {
            ret = ret / i * (i - 1);
            while (x % i == 0) {
                x /= i;
            }
        }
    }
    if (x > 1) {
        ret = ret / x * (x - 1);
    }
    return ret;
}

// 处理大指数b（字符串形式），返回b mod phi + (b >= phi ? phi : 0)
LL process_b(const string& s, LL phi) {
    LL t = 0;
    bool flag = false;  // 标记b是否 >= phi
    for (char ch : s) {
        t = t * 10 + (ch - '0');
        if (t >= phi) {
            flag = true;
            t %= phi;  // 边计算边取模，避免溢出
        }
    }
    if (flag) {
        t += phi;  // 满足b >= phi，加上phi
    }
    return t;
}

// 快速幂计算 (a^b) mod p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    a = a % p;
    while (b > 0) {
        if (b & 1) {
            ret = ret * a % p;
        }
        a = a * a % p;
        b >>= 1;
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    LL a, m;
    string s;
    cin >> a >> m >> s;
    
    if (m == 1) {  // 特殊情况：mod 1 结果恒为0
        cout << 0 << endl;
        return 0;
    }
    
    LL phi = get_phi(m);
    LL b = process_b(s, phi);
    LL ans = qpow(a, b, m);
    cout << ans << endl;
    
    return 0;
}

五、实战例题 2：洛谷 P4139 上帝与集合的正确用法

题目链接：https://www.luogu.com.cn/problem/P4139

5.1 题目分析

题目描述 ：定义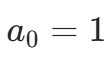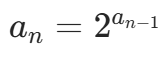，​，求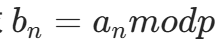 稳定后的结果（即某一项后不再变化的值）。

输入描述：第一行一个整数 T，表示数据组数；接下来 T 行，每行一个正整数 p。

输出描述：T 行，每行一个整数，表示稳定后的结果。

示例输入：3236

示例输出：014

核心难点：

1. 序列 an 增长极快（a1=2，a2=4，a3=16，a4=216=65536，后续指数远超存储范围）；
2. 需利用扩展欧拉定理递归降幂，直到模数为 1（此时结果恒为 0）。

5.2 解题思路

观察序列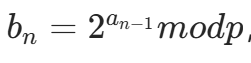，由于​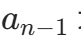 增长极快，当 n 足够大时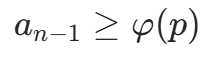，，根据扩展欧拉定理：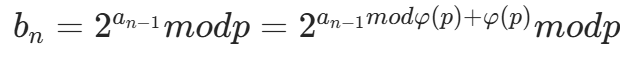

而 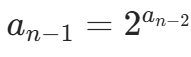，因此可递归应用扩展欧拉定理，直到模数 p=1（此时结果为 0）。递归边界为：当 p=1 时，返回 0。

具体递归公式：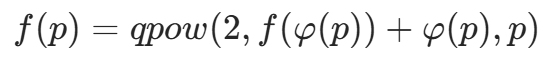

其中 f(p) 表示稳定后的结果。

5.3 C++ 实现（预处理欧拉函数 + 递归）

由于 p 可能较大（可达 1e7），直接递归计算每个 p 的欧拉函数会重复计算，因此先预处理 1e7 以内的所有欧拉函数，再进行递归。

C++ 实现

#include <iostream>
#include <cstring>
using namespace std;

typedef long long LL;
const int MAXN = 1e7 + 10;

bool st[MAXN];       // 标记是否为合数
int primes[MAXN], cnt;  // 存储质数
int phi[MAXN];       // 存储欧拉函数值

// 线性筛（欧拉筛）预处理1~MAXN的欧拉函数
void pre_phi() {
    memset(st, false, sizeof st);
    memset(phi, 0, sizeof phi);
    cnt = 0;
    phi[1] = 1;
    for (int i = 2; i <= MAXN; ++i) {
        if (!st[i]) {  // i是质数
            primes[++cnt] = i;
            phi[i] = i - 1;
        }
        // 枚举所有已找到的质数，筛掉i*primes[j]
        for (int j = 1; 1LL * i * primes[j] <= MAXN; ++j) {
            int x = i * primes[j];
            st[x] = true;
            if (i % primes[j] == 0) {  // primes[j]是i的最小质因子
                phi[x] = phi[i] * primes[j];
                break;
            } else {  // primes[j]不是i的质因子，i与primes[j]互质
                phi[x] = phi[i] * (primes[j] - 1);
            }
        }
    }
}

// 快速幂计算 (a^b) mod p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    a = a % p;
    while (b > 0) {
        if (b & 1) {
            ret = ret * a % p;
        }
        a = a * a % p;
        b >>= 1;
    }
    return ret;
}

// 递归计算稳定后的结果
int dfs(int p) {
    if (p == 1) {
        return 0;
    }
    // 递归应用扩展欧拉定理
    return qpow(2, dfs(phi[p]) + phi[p], p);
}

int main() {
    pre_phi();  // 预处理欧拉函数
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int T;
    cin >> T;
    while (T--) {
        int p;
        cin >> p;
        cout << dfs(p) << endl;
    }
    return 0;
}

5.4 代码分析与优化

• 预处理欧拉函数：使用线性筛（欧拉筛）在 O(MAXN) 时间内预处理 1e7 以内的欧拉函数，后续递归查询时直接调用，避免重复计算；
• 递归深度：由于欧拉函数每次至少减半（对于 p>2，φ(p)<p），递归深度为 O(logp)，不会栈溢出；
• 时间复杂度：预处理时间 O(1e7)（约 1 秒），每组查询时间 O(logp×logb)（b 为降幂后的指数），对于 T=1e5 组数据也能快速响应；
• 空间优化：1e7 级别的数组占用约 40MB（int 类型），在竞赛允许的内存范围内。

六、常见误区与避坑指南

6.1 扩展欧拉定理的降幂规则记错

• 误区 ：将 b≥φ(m) 时的降幂规则记为 ，忽略加 φ(m)；
• 反例：a=2，m=4，b=10，若直接降幂为 10 mod 2=0，则 2^{0}=1 mod 4=1，与正确结果 0 不符；
• 避坑 ：牢记 "指数大于等于 φ(m) 时，降幂后需加 φ(m)"，即。

6.2 欧拉函数计算错误

• 误区：分解质因数时未除尽所有倍数，导致漏算质因子；
• 示例：计算 φ(12) 时，若只除以 2 一次（未除尽 4），则会误将质因子 2 重复计算，导致结果错误；
• 避坑 ：分解质因数时，用 while (x % i == 0) x /= i 确保除尽当前质因子的所有倍数。

6.3 大指数处理时溢出

• 误区：直接将字符串形式的大指数转换为整数存储，导致溢出；
• 避坑：边读入边计算 bmodφ(m)，同时标记 b 是否大于等于 φ(m)，无需存储完整的大指数。

6.4 忽略模数为 1 的特殊情况

• 误区：当 m=1 时，仍按常规流程计算，导致无用功；
• 避坑：任何数 mod 1 都为 0，直接返回 0 即可。

6.5 递归时未处理边界条件

• 误区：递归计算 f(p) 时，未处理 p=1 的边界，导致无限递归；
• 避坑：明确递归边界：当 p=1 时，返回 0。

---

总结

欧拉定理与扩展欧拉定理是处理大指数幂取模问题的核心工具，其核心价值在于 "降幂"------ 将无法直接计算的超大指数转化为可计算的小指数。

如果在学习过程中遇到具体题目无法解决，或想了解快速乘、组合数取模等延伸知识点，可以随时留言交流。后续将持续更新数论进阶内容，敬请关注！