【数据结构】从零开始认识图论 --- 单源/多源最短路算法

挫折会来也会过去，
热泪会流下也会收起，
没有什么可以让我气馁的，
因为，我有着长长的一生。
--- 席慕蓉《写给幸福》---

从零开始认识图论

[1 单源最短路算法](#1 单源最短路算法)
- [1.1 Dijkstra算法](#1.1 Dijkstra算法)
- [1.2 Bellman-Ford算法](#1.2 Bellman-Ford算法)
[2 多源最短路算法](#2 多源最短路算法)

1 单源最短路算法

求图的最短路，如果使用传统的bfs / dfs ，那么就要对一个节点进行扩散，遍历所有节点，如果图内部是邻接矩阵的实现，时间复杂度就会到了O(n^3)，而且最重要的是只能处理权值0/1的！因为传统的bfs是根据边数进行处理的。

在单源最短路算法有两个经典的算法：

对于无负权值的场景：无负权值的场景可以完美的使用高效的Dijkstra算法，只需要O(n^2)的时间复杂度就能解决最短路问题
对于无负权值的场景：负值的出现会扰乱正常的处理逻辑，有了负权值就说明即使是已经确定过的最短路径在未来出现一个负值可能会被颠覆。

1.1 Dijkstra算法

这个算法的核心思想是贪心，通过对局部路径的最短选择已达到最优的选择。

Dijkstra算法 适用于解决带权重的有向图上的单源最短路径问题，同时算法要求图中所有边的权重非负 。一般在求解最短路径的时候都是已知一个起点和一个终点，所以使用Dijkstra算法求解过后也就得到了所需起点到终点的最短路径。

算法思路：

针对一个带权有向图G，将所有结点分为两组S和Q：
- S 是已经确定最短路径的结点集合，在初始时为空（初始时就可以将源节点s放入，毕竟源节点到自己的代价是0）
- Q 为其余未确定最短路径的结点集合
每次从Q 中找出一个起点到该结点代价最小的结点u ，将u 从Q 中移出，并放入S中，对 u 的每一个相邻结点 v 进行松弛操作(即对u关联的边进行松弛操作)。
松弛操作 即对每一个相邻结点v ，判断源 s到 u 的代价与 u 到 v 的代价之和 是否比原来 s 到 v 的代价更小，若代价比原来小，则要将 s 到v 的代价更新为s 到 u 与 u 到 v 的代价之和，否则维持原样。
如此一直循环直至集合Q 为空，即所有节点都已经查找过一遍并确定了最短路径
至于一些起点到达不了的结点在算法循环后其代价仍为初始设定的值，不发生变化。
Dijkstra算法每次都是选择U-S中最小的路径节点来进行更新，并加入S中，所以该算法使用的是贪心策略。

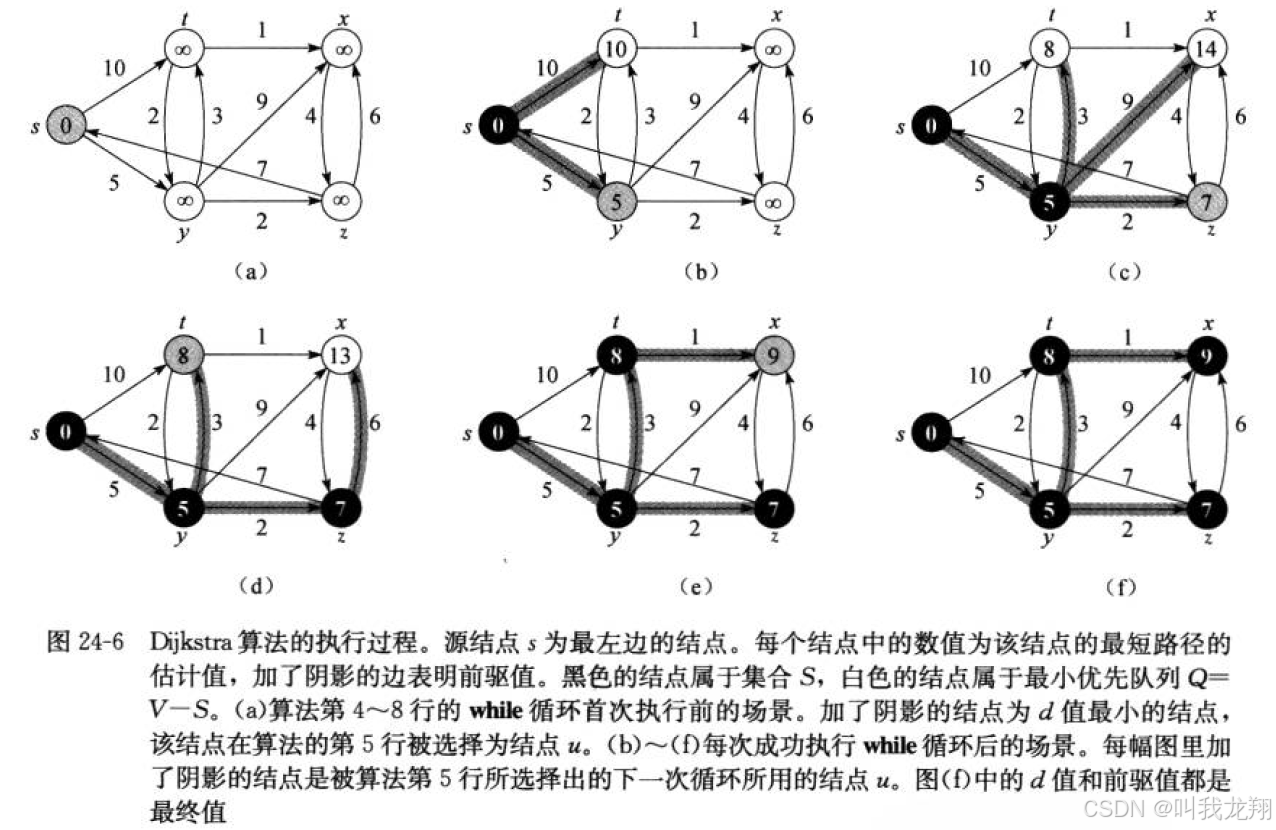
Dijkstra算法存在的问题是不支持图中带负权路径，如果带有负权路径，则可能会找不到一些路径的最短路径。

cpp 复制代码

//最短路算法
//					起点				最短路径		 当前节点的前一个节点
void Dijkstra(const T& src, vector<W>& dist, vector<int>& pPath)
{
	//Dijkstra的核心是 寻找srci到 未确定最短路的节点集合 的最短边
	//然后根据这个最短边更新涉及的节点的最短值
	//初始化
	dist.resize(_size, MAX_W);
	pPath.resize(_size, -1);
	size_t srci = _vIndexs[src];//获取起始点

	vector<bool> vis(_size , false);//是否确定了最短路
	dist[srci] = 0;

	//循环处理 _size 个节点
	for (int i = 0; i < _size; i++) {
		//寻找最近路的节点	
		int min = MAX_W;
		int index = -1;
		for (int j = 0; j < _size; j++) {
			if (vis[j] == false && dist[j] < min) {
				min = dist[j];
				index = j;
			}
		}
		//找到当前最短路节点 设置已确定
		vis[index] = true;
		//处理该节点引申出的边
		for (int k = 0; k < _size; k++) {
			//(srci -> index) + (index -> k)  < (srci -> k)
			if (vis[k] == false && _map[index][k] != MAX_W
				&& dist[index] + _map[index][k] < dist[k]) {
				dist[k] = dist[index] + _map[index][k];
				pPath[k] = index;
			}
		}
	}
}

1.2 Bellman-Ford算法

对于出现了负权值的图，只能降低时间复杂度，以避免缺少处理
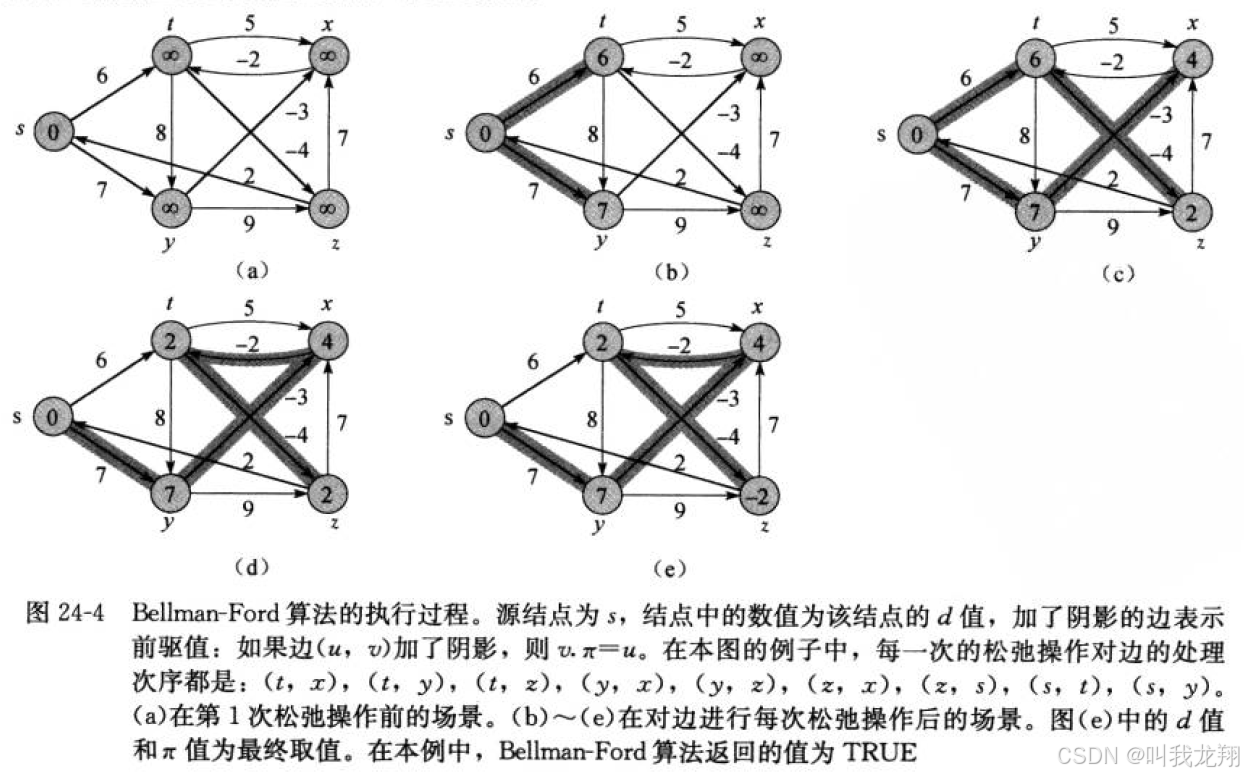
bellman-ford算法 可以解决负权图的单源最短路径问题。它的优点是可以解决有负权边的单源最短路径问题，而且可以用来判断是否有负权回路。它也有明显的缺点，它的时间复杂度 O(N*E) (N是点数，E是边数)普遍是要高于Dijkstra算法O(N²)的。像这里如果我们使用邻接矩阵实现，那么遍历所有边的数量的时间复杂度就是O(N^3)，这里也可以看出来Bellman-Ford就是一种暴力求解更新。

Bellman-Ford算法的核心是松弛操作，进行n-1轮松弛，保证所有可能都被验证过。
"最多需要 n-1 次循环（松弛操作）" 的核心原因是：图中任意两点间的最短路径（若存在）最多包含 n-1 条边（n 为节点总数）。也就是说更新n-1次会找到u->v的所以可能的最短路径
最后进行一次负权值检测：如果松弛操作还能进行更新，说明存在负权值的回路！
存在负权值的回路的情况就不存在最短回路，最短就不存在意义了

cpp 复制代码

//处理带负权的最短路算法
bool BellmanFord(const T& src, vector<W>& dist, vector<int>& pPath) {
	//核心思路
	//对每个节点枚举所有的边 
	//满足 (srci->i + (i->j) < (srci->j) 则可以进行更新最短路
	//
	//初始化
	dist.resize(_size, MAX_W);
	pPath.resize(_size, -1);
	size_t srci = _vIndexs[src];//获取起始点

	vector<bool> vis(_size, false);//是否确定了最短路
	dist[srci] = 0;
	for (int k = 0; k < _size; k++) {
		//优化 避免进行多余的更新轮次
		bool exchange = false;
		for (int i = 0; i < _size; i++) {
			for (int j = 0; j < _size; j++) {
				//存在边且新路径小于原路径
				if (_map[i][j] != MAX_W && dist[i] + _map[i][j] < dist[j]) {
					exchange = true;
					dist[j] = dist[i] + _map[i][j];
					pPath[j] = i;
				}

			}
		}
		if (exchange == false)
			break;
	}
	
	for (int i = 0; i < _size; i++) {
		for (int j = 0; j < _size; j++) {
			//存在边且新路径小于原路径
			if (_map[i][j] != MAX_W && dist[i] + _map[i][j] < dist[j]) {
				return false;//存在负权回路导致无限次处理
			}
		}
	}

	return true;
}

2 多源最短路算法

不同于单源的最短路算法思想（贪心，暴力），多源最短路的经典Floyd-Warshall算法是以动态规划的思想。

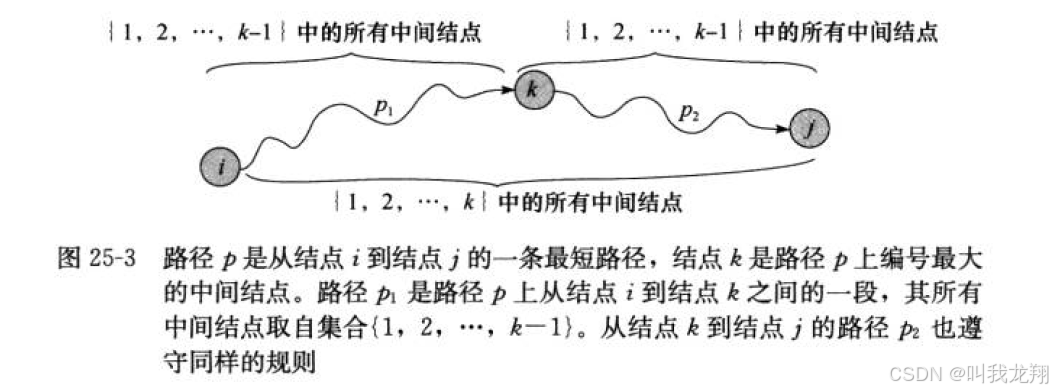
其思想是D[i][j][k]表示（i->j）中从 [0 , k]节点集合中能取到的最短路径，状态转移方程为：

cpp 复制代码

void FloydWarShall(vector<vector<W>>& vvDist, vector<vector<int>>& vvPPath) {
	//多源最短路径算法
	//动态规划解决问题
	//D[i][j][k]表示 i节点到j节点 从(0 , k)中的节点中最短路径的集合
	//对于第k个节点可以选择 也可以不选
	//选择第K个节点 则可以通过k节点进行中转 D[i][j][k] = D[i][k][k-1] + D[k][j][k-1]
	//不选择       D[i][j][k] = D[i][j][k - 1]
	//D[i][j][k] = min(D[i][j][k - 1] , D[i][k][k-1] + D[k][j][k-1])

	//vvDist[i][j]表示 i->j的最短路径
	//vvPPath[i][j]表示 i->j的最短路径中 j的上一个节点是谁
	//初始化
	vvDist.resize(_size, vector<W>(_size, MAX_W));
	vvPPath.resize(_size, vector<int>(_size, -1));

	//初始化继承边关系
	for (int i = 0; i < _size; i++) {
		for (int j = 0; j < _size; j++) {
			if (_map[i][j] != MAX_W) {
				vvDist[i][j] = _map[i][j];
				vvPPath[i][j] = i;
			}
			if (i == j) {
				vvDist[i][j] = 0;
				vvPPath[i][j] = -1;
			}
		}
	}
	//进行处理
	for (int k = 0; k < _size; k++) {
		for (int i = 0; i < _size; i++) {
			for (int j = 0; j < _size; j++) {
				//// i->k + k->j 比 i->j前面更新的距离更短，则更新
				if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W  //保证两个权值是存在的
					&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j]) {//判断是否可以更新
					vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
					vvPPath[i][j] = vvPPath[k][j];//路径后半段是 k->j组成的
				}

			}
		}
	}
}