1、爬楼梯 hot

分析:
状态表示:爬 i 阶楼梯最多有 dp[i] 种不同走法。
状态转移方程:i = 1 时会越界,单独处理,dp[1]=1;i=2 时,会获取 dp[0],也单独处理,dp[2] = 2。
从 index=3 开始遍历填表,dp[n] 就是答案。
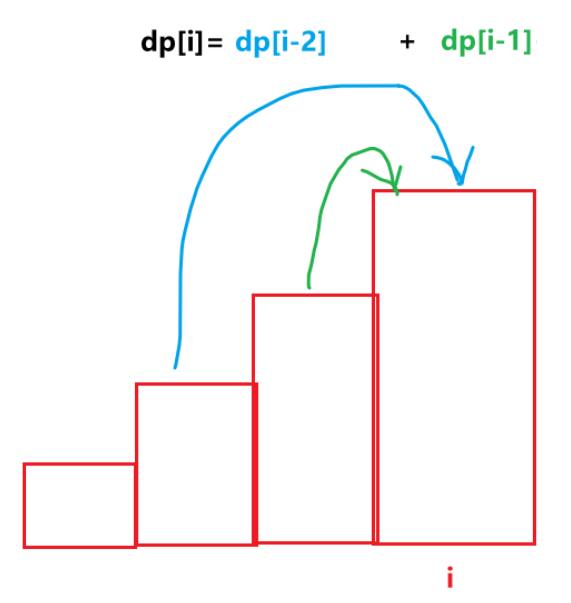
代码:时间复杂度:O(n)。
java
class Solution {
public int climbStairs(int n) {
if (n==1) return 1;
int[] dp = new int[n+1];
dp[1] = 1;
dp[2] = 2;
for (int i=3; i <= n; i++)
dp[i] = dp[i-1]+dp[i-2];
return dp[n];
}
}2、杨辉三角 hot
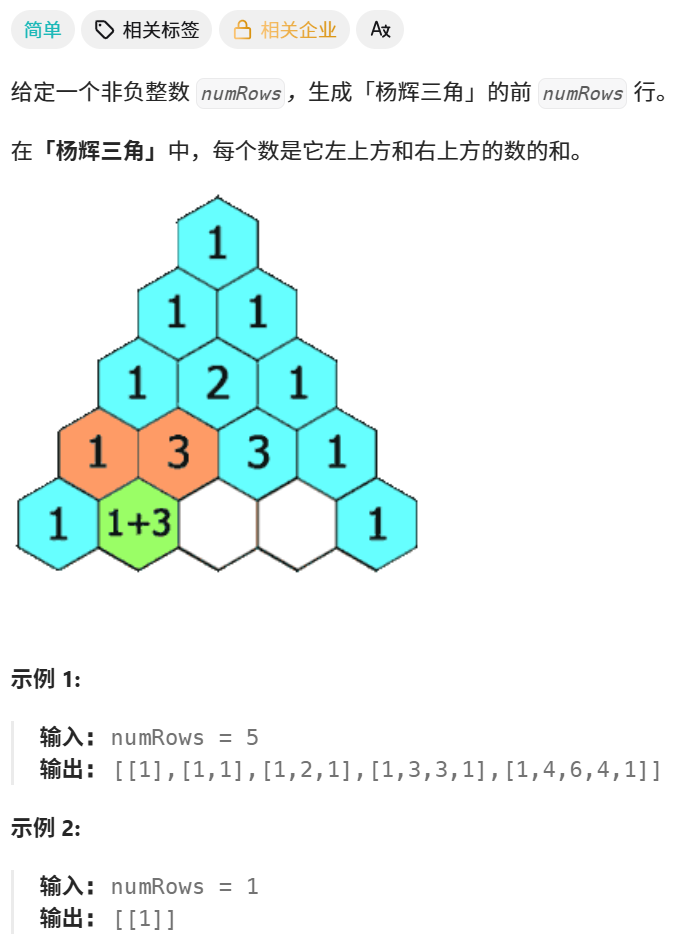
分析:遍历 i=0~numRows-1 行,遍历 j=0~i 列。每行首、尾是1;其余=上方+左上方 之和。时间复杂度 O(n^2)。
状态表示:dp[i][j] 表示第 i 行第 j 列的元素值。
状态转移方程:j=0, i, dp[i][j] = 1。其余,dp[i][j]=dp[i-1][j]+dp[i-1][j-1]。若 i=0 会越界,单独处理 dp[0][0]=1。
代码:
java
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> result = new ArrayList<>();
// 处理第一行
List<Integer> tmp = new ArrayList<>();
tmp.add(1);
result.add(tmp);
// 处理剩余行
for (int i = 1; i < numRows; i++) {
tmp = new ArrayList<>();
for (int j = 0; j <= i; j++) {
if (j==0 || j==i) tmp.add(1);
else {
List<Integer> preRow = result.get(i-1);
tmp.add(preRow.get(j) + preRow.get(j-1));
}
}
result.add(tmp);
}
return result;
}
}3、打家劫舍 hot

分析:
状态表示:偷窃到 i 位置房屋,最多能偷多少。
状态转换方程:
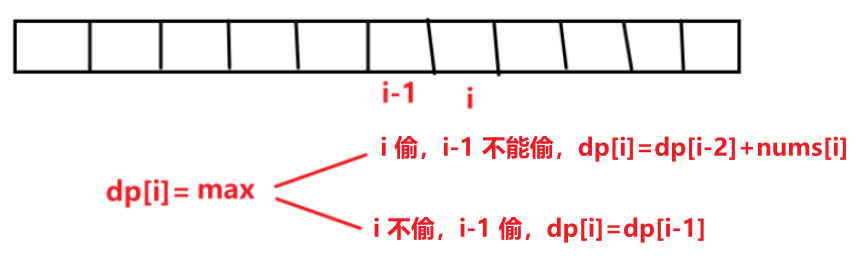
i=0,1 时会越界,单独处理。dp[0]=nums[0],dp[1]=max(nums[0], nums[1])。
代码:时间复杂度 O(n)。
java
class Solution {
public int rob(int[] nums) {
int n = nums.length;
if (n==1) return nums[0];
int[] dp = new int[n];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < n; i++)
dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i]);
return dp[n-1];
}
}4、分割等和子集 hot
题目 :416. 分割等和子集 - 力扣(LeetCode)
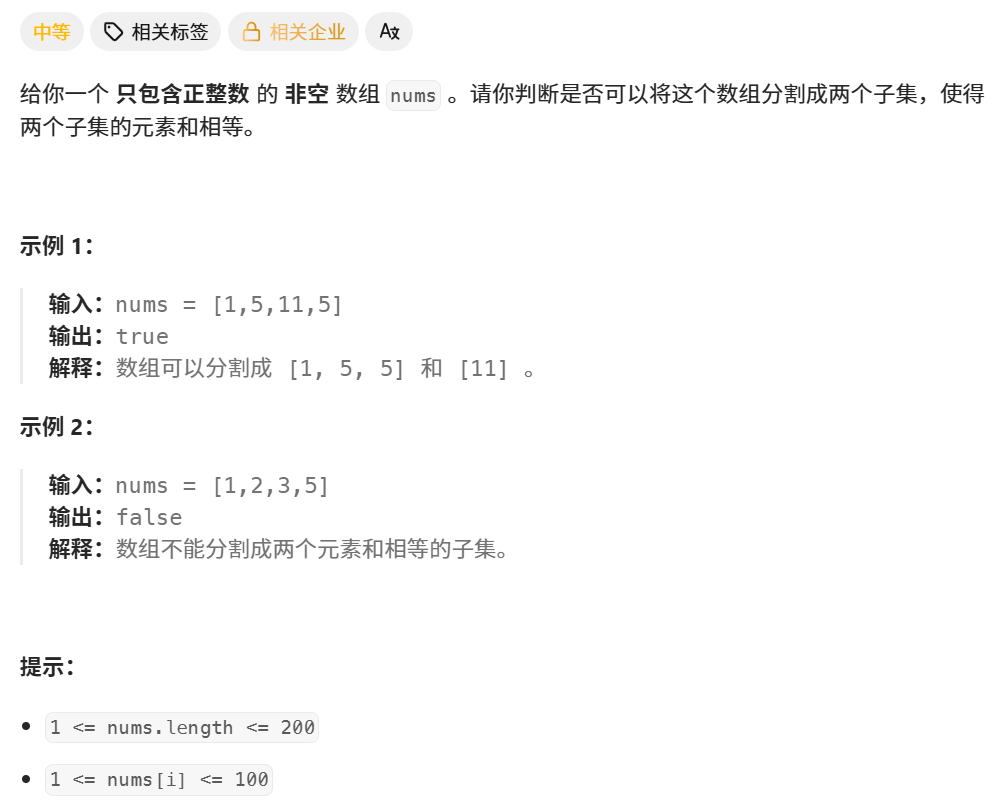
分析:换一个说法,从数组中选出一些数字,让他们的和刚好为总和 sum 的一半。即 0-1 背包问题(从前 i 个物品选,每个物品只有一个(无限个就是完全背包),重量刚好为 w,的最大价值)。
状态表示:dp[i][j] 表示是否能在 [0,i] 中选取数字,和恰好等于 sum/2。
状态转移方程:

初始化:dp[0][0] 表示从0个数中选,刚好和为 0,true;dp[0][j] 表示从0个数中选,刚好和为 j (j > 0),false;dp[i][0] 表示从 i 个数中选,刚好和为0,就是不选,true。
特殊情况:n=1,不能分,返回 false;sum 为奇数,sum/2 为小数,选不出和为小数的,返回 false。
注意:dp[i][j] 表示前 i 个数中选,因此第 i 个数对应 nums[i-1]。
时间复杂度:O(n*sum/2),空间复杂度:O(n*sum/2)
空间优化:实际上更新每一行 dp,都是从上一行的 j 前的 dp 取值计算的。我们两层循环的目的,就是防止本层跟新的值,把 j 前需要取的值给覆盖了。换个思路:倒着更新,就不会把 j 前的值给覆盖掉了。
代码:
java
class Solution {
public boolean canPartition(int[] nums) {
int n = nums.length;
if (n == 1) return false;
int sum = 0;
for (int num : nums) sum += num;
if (sum % 2 == 1) return false;
sum = sum/2;
boolean[][] dp = new boolean[n+1][sum+1];
for (int i = 0; i <= n; i++) dp[i][0] = true;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= sum; j++) {
if (j - nums[i-1] >= 0) dp[i][j] = dp[i-1][j-nums[i-1]] || dp[i-1][j];
else dp[i][j] = dp[i-1][j];
}
}
return dp[n][sum];
}
}方法:dp 去掉行。
java
class Solution {
public boolean canPartition(int[] nums) {
int n = nums.length;
if (n == 1) return false;
int sum = 0;
for (int num : nums) sum += num;
if (sum % 2 == 1) return false;
sum = sum/2;
boolean[] dp = new boolean[sum+1];
dp[0] = true;
for (int i = 1; i <= n; i++) {
for (int j = sum; j >= nums[i-1]; j--)
dp[j] = dp[j-nums[i-1]] || dp[j];
}
return dp[sum];
}
}5、最长有效括号 hot

分析:
dp[i] 表示以 i 结尾的最长有效括号,的长度。
i 处为 (,dp[i] 必为 0。
i 处为 ),dp[i] 分两种情况。
情况1,i-1 是 (:
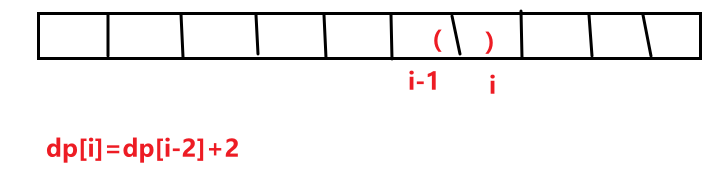
情况2,i-1 是 ),且 m 位置是 (:
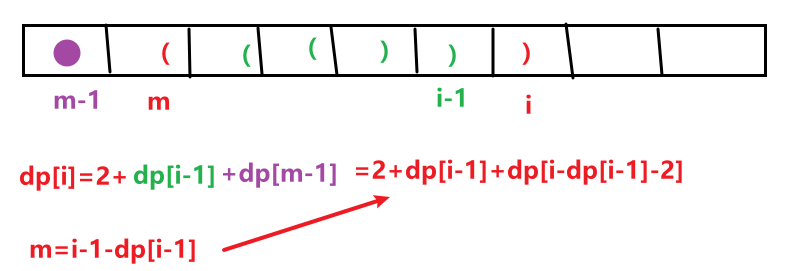
特殊处理:因为 i=0,1 时会越界,单独处理。dp[0]=0;dp[1]=2(若是 ();否则 dp[1]=0)。
最终结果:dp 中的最大值。
时间复杂度:O(n),空间复杂度:O(n)。
代码:注意,取 chars[m] 和 dp[m-1] 时,m 和 m-1 都不能越界。
java
class Solution {
public int longestValidParentheses(String s) {
if (s.length() == 0 || s.length() == 1) return 0;
char[] chars = s.toCharArray();
int n = chars.length;
int[] dp = new int[n];
dp[0] = 0;
if (chars[0] == '(' && chars[1] == ')') dp[1] = 2;
else dp[1] = 0;
int maxLen = dp[1];
for (int i = 2; i < n; i++) {
if (chars[i] == ')') {
int m = i-1-dp[i-1];
if (chars[i-1] == '(') dp[i] = dp[i-2]+2;
else if (m >=0 && chars[m] == '(') dp[i] = 2 + dp[i-1] + (m >= 1 ? dp[m-1] : 0);
}
maxLen = Math.max(maxLen, dp[i]);
}
return maxLen;
}
}