SLAM中的非线性优-3D图优化之轴角在Opencv-PNP中的应用（一）

从本节开始讲解3D图优化，3D的优化算法位姿表示主要以轴角，四元数以及李群李代数表示为主，目前先从PNP中的轴角开始，先看问题描述；

总结：

上述即为pnp求解的基本过程，详细雅可比请继续往下看，先看源码部分

复制代码

void projectPoints(const std::vector<Point3d> &inlier_landmarks,
                   const std::vector<Point3d> &inlier_bearings,
                   const Vector3d &rotation_vector,
                   const Vector3d &translation_vector,
                   MatrixXd &dpdrot, MatrixXd &dpdt,
                   Eigen::MatrixXd &reproject_err,
                   const bool &calc_derivative)
{

    double k[14] = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, fx = fx_, fy = fy_, cx = cx_, cy = cy_;

    Matrix3d matR;
    Vector3d r, t = translation_vector;
    MatrixXd dRdr = Eigen::MatrixXd(3, 9);

    Matrix3d matTilt = Matrix3d::Identity();

    rodrigues(rotation_vector, matR, dRdr);

    uint32_t i, j, count;
    count = inlier_landmarks.size();

    reproject_err = Eigen::MatrixXd(2 * count, 1);

    for (i = 0; i < count; i++)
    {
    	// 世界系下3D点转相机系
        const Vector3d &pos_w = inlier_landmarks.at(i);

        Point3d pc = matR * pos_w + t;

        float64_t X = pos_w[0], Y = pos_w[1], Z = pos_w[2];
        float64_t x = pc[0];
        float64_t y = pc[1];
        float64_t z = pc[2];
        float64_t r2, r4, r6, a1, a2, a3, cdist, icdist2;
        float64_t xd, yd, xd0, yd0, invProj;
        Vector3d vecTilt;
        Vector3d dVecTilt;
        Eigen::Matrix2d dMatTilt;
        Vector2d dXdYd;

        // 归一化坐标
        z = z ? 1. / z : 1;
        x *= z;
        y *= z;
	
	// 径向畸变
        r2 = x * x + y * y;
        r4 = r2 * r2;
        r6 = r4 * r2;
        a1 = 2 * x * y;
        a2 = r2 + 2 * x * x;
        a3 = r2 + 2 * y * y;
        cdist = 1 + k[0] * r2 + k[1] * r4 + k[4] * r6;
        
        // 切向畸变
        icdist2 = 1. / (1 + k[5] * r2 + k[6] * r4 + k[7] * r6);
        xd0 = x * cdist * icdist2 + k[2] * a1 + k[3] * a2 + k[8] * r2 + k[9] * r4;
        yd0 = y * cdist * icdist2 + k[2] * a3 + k[3] * a1 + k[10] * r2 + k[11] * r4;

        // additional distortion by projecting onto a tilt plane
        vecTilt = matTilt * Vector3d(xd0, yd0, 1);
        invProj = vecTilt(2) ? 1. / vecTilt(2) : 1;
        xd = invProj * vecTilt(0);
        yd = invProj * vecTilt(1);

        double ptx = xd * fx + cx;
        double pty = yd * fy + cy;

        const Vector3d &norm_point = inlier_bearings.at(i);
        
	// 重投影误差
        reproject_err(2 * i, 0) = ptx - (norm_point[0] / norm_point[2] * fx + cx);
        reproject_err(2 * i + 1, 0) = pty - (norm_point[1] / norm_point[2] * fy + cy);

        if (calc_derivative)
        {

            for (int row = 0; row < 2; ++row)
                for (int col = 0; col < 2; ++col)
                    dMatTilt(row, col) = matTilt(row, col) * vecTilt(2) - matTilt(2, col) * vecTilt(row);
            double invProjSquare = (invProj * invProj);
            dMatTilt *= invProjSquare;

            // dpdt 对平移的导数
            double dxdt[] = {z, 0, -x * z}, dydt[] = {0, z, -y * z};
            for (j = 0; j < 3; j++)
            {
                double dr2dt = 2 * x * dxdt[j] + 2 * y * dydt[j];
                double dcdist_dt = k[0] * dr2dt + 2 * k[1] * r2 * dr2dt + 3 * k[4] * r4 * dr2dt;
                double dicdist2_dt = -icdist2 * icdist2 * (k[5] * dr2dt + 2 * k[6] * r2 * dr2dt + 3 * k[7] * r4 * dr2dt);
                double da1dt = 2 * (x * dydt[j] + y * dxdt[j]);
                double dmxdt = (dxdt[j] * cdist * icdist2 + x * dcdist_dt * icdist2 + x * cdist * dicdist2_dt +
                                k[2] * da1dt + k[3] * (dr2dt + 4 * x * dxdt[j]) + k[8] * dr2dt + 2 * r2 * k[9] * dr2dt);
                double dmydt = (dydt[j] * cdist * icdist2 + y * dcdist_dt * icdist2 + y * cdist * dicdist2_dt +
                                k[2] * (dr2dt + 4 * y * dydt[j]) + k[3] * da1dt + k[10] * dr2dt + 2 * r2 * k[11] * dr2dt);
                dXdYd = dMatTilt * Vector2d(dmxdt, dmydt);

                dpdt(2 * i, j) = fx * dXdYd(0);
                dpdt(2 * i + 1, j) = fy * dXdYd(1);
            }

            // dpdr 对旋转的导数
            double dx0dr[] =
                {
                    X * dRdr(0, 0) + Y * dRdr(0, 1) + Z * dRdr(0, 2),
                    X * dRdr(1, 0) + Y * dRdr(1, 1) + Z * dRdr(1, 2),
                    X * dRdr(2, 0) + Y * dRdr(2, 1) + Z * dRdr(2, 2)};
            double dy0dr[] =
                {
                    X * dRdr(0, 3) + Y * dRdr(0, 4) + Z * dRdr(0, 5),
                    X * dRdr(1, 3) + Y * dRdr(1, 4) + Z * dRdr(1, 5),
                    X * dRdr(2, 3) + Y * dRdr(2, 4) + Z * dRdr(2, 5)};
            double dz0dr[] =
                {
                    X * dRdr(0, 6) + Y * dRdr(0, 7) + Z * dRdr(0, 8),
                    X * dRdr(1, 6) + Y * dRdr(1, 7) + Z * dRdr(1, 8),
                    X * dRdr(2, 6) + Y * dRdr(2, 7) + Z * dRdr(2, 8)};
                    
	    // 归一化坐标对旋转
            for (j = 0; j < 3; j++)
            {
                double dxdr = z * (dx0dr[j] - x * dz0dr[j]);
                double dydr = z * (dy0dr[j] - y * dz0dr[j]);
                double dr2dr = 2 * x * dxdr + 2 * y * dydr;
                double dcdist_dr = (k[0] + 2 * k[1] * r2 + 3 * k[4] * r4) * dr2dr;
                double dicdist2_dr = -icdist2 * icdist2 * (k[5] + 2 * k[6] * r2 + 3 * k[7] * r4) * dr2dr;
                double da1dr = 2 * (x * dydr + y * dxdr);
                double dmxdr = (dxdr * cdist * icdist2 + x * dcdist_dr * icdist2 + x * cdist * dicdist2_dr +
                                k[2] * da1dr + k[3] * (dr2dr + 4 * x * dxdr) + (k[8] + 2 * r2 * k[9]) * dr2dr);
                double dmydr = (dydr * cdist * icdist2 + y * dcdist_dr * icdist2 + y * cdist * dicdist2_dr +
                                k[2] * (dr2dr + 4 * y * dydr) + k[3] * da1dr + (k[10] + 2 * r2 * k[11]) * dr2dr);

        
                dXdYd = dMatTilt * Vector2d(dmxdr, dmydr);
         
                dpdrot(2 * i, j) = fx * dXdYd(0);
                dpdrot(2 * i + 1, j) = fy * dXdYd(1);
            }
        }
    }
}

上述除了旋转的雅可比推导外，其他的都比较简单，接下来看旋转雅可比推导，

（1）旋转矩阵对旋转向量的导数

根据罗德里格斯公式，以及导数定义

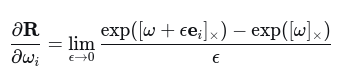
按照李群李代数推导，很容易获得

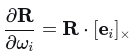
代码中实现

复制代码

MatrixXd dRdr = Eigen::MatrixXd(3, 9);  // 3×9矩阵，存储9个导数分量
rodrigues(rotation_vector, matR, dRdr);

这里 dRdr 存储的是：

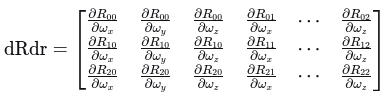
（2）相机坐标对旋转的导数

相机坐标系下的点：

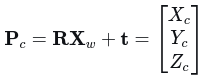
对旋转分量求导：

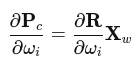
展开分量形式：

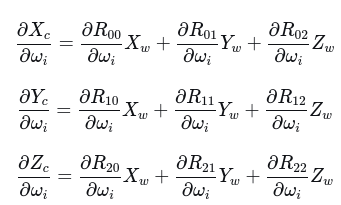
代码实现

复制代码

double dx0dr[] = {
    X * dRdr(0, 0) + Y * dRdr(0, 1) + Z * dRdr(0, 2),  // ∂Xc/∂ωx, ∂Xc/∂ωy, ∂Xc/∂ωz
    X * dRdr(1, 0) + Y * dRdr(1, 1) + Z * dRdr(1, 2),
    X * dRdr(2, 0) + Y * dRdr(2, 1) + Z * dRdr(2, 2)};

double dy0dr[] = {
    X * dRdr(0, 3) + Y * dRdr(0, 4) + Z * dRdr(0, 5),  // ∂Yc/∂ωx, ∂Yc/∂ωy, ∂Yc/∂ωz  
    X * dRdr(1, 3) + Y * dRdr(1, 4) + Z * dRdr(1, 5),
    X * dRdr(2, 3) + Y * dRdr(2, 4) + Z * dRdr(2, 5)};

double dz0dr[] = {
    X * dRdr(0, 6) + Y * dRdr(0, 7) + Z * dRdr(0, 8),  // ∂Zc/∂ωx, ∂Zc/∂ωy, ∂Zc/∂ωz
    X * dRdr(1, 6) + Y * dRdr(1, 7) + Z * dRdr(1, 8),
    X * dRdr(2, 6) + Y * dRdr(2, 7) + Z * dRdr(2, 8)};

（3）归一化坐标对旋转的导数

归一化坐标：

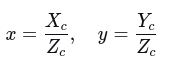
使用商法则求导：

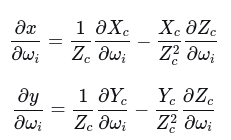
代码实现

复制代码

for (j = 0; j < 3; j++)  // j遍历ωx, ωy, ωz
{
    double dxdr = z * (dx0dr[j] - x * dz0dr[j]);  // z = 1/Zc
    double dydr = z * (dy0dr[j] - y * dz0dr[j]);
    // dxdr = (1/Zc)(∂Xc/∂ωj) - (Xc/Zc²)(∂Zc/∂ωj)
    // dydr = (1/Zc)(∂Yc/∂ωj) - (Yc/Zc²)(∂Zc/∂ωj)
}

（4）畸变坐标对归一化坐标的导数

畸变模型：

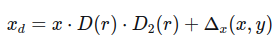
其中D(r), D2(r)跟delta(x,y) 分别表示（主径向畸变），（额外径向畸变倒数），（切向畸变）

对x求导

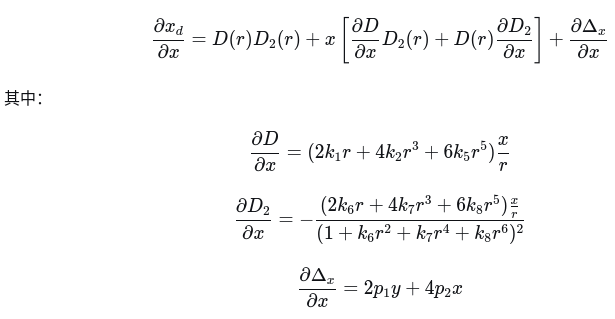
代码实现

复制代码

double dr2dr = 2 * x * dxdr + 2 * y * dydr;  // ∂r²/∂ωj
double dcdist_dr = (k[0] + 2 * k[1] * r2 + 3 * k[4] * r4) * dr2dr;  // ∂D/∂ωj
double dicdist2_dr = -icdist2 * icdist2 * (k[5] + 2 * k[6] * r2 + 3 * k[7] * r4) * dr2dr;  // ∂D₂/∂ωj

double da1dr = 2 * (x * dydr + y * dxdr);  // ∂(2xy)/∂ωj

double dmxdr = (dxdr * cdist * icdist2 +  // 第一项：∂x/∂ωj × D × D₂
                x * dcdist_dr * icdist2 +  // 第二项：x × ∂D/∂ωj × D₂  
                x * cdist * dicdist2_dr +  // 第三项：x × D × ∂D₂/∂ωj
                k[2] * da1dr +            // 切向畸变部分
                k[3] * (dr2dr + 4 * x * dxdr) + 
                (k[8] + 2 * r2 * k[9]) * dr2dr);  // 额外畸变项

（5）完整的旋转雅可比矩阵

代码实现

复制代码

dXdYd = dMatTilt * Vector2d(dmxdr, dmydr);  // 倾斜投影平面的额外变换

dpdrot(2 * i, j) = fx * dXdYd(0);     // ∂u/∂ωj
dpdrot(2 * i + 1, j) = fy * dXdYd(1); // ∂v/∂ωj

总结：

本节总结了3D-2D重投影误差的残差跟雅可比推导，其中旋转部分还是主要还是以李群李代数方式推导最简单，下一讲及后续章节，将以轴角跟四元数方式推导