




这里有一个细节的点是单位矩阵E∗A=A∗EE*A=A*EE∗A=A∗E,所以可以直接写4XXT4XX^T4XXT


这里D=∣AABEO∣D=\begin{vmatrix} A & AB \\ E & O \\ \end{vmatrix}D= AEABO 的原因并没有给出,可以通过列变换,第一列乘以B加到第二列,其中-E * B + B = O

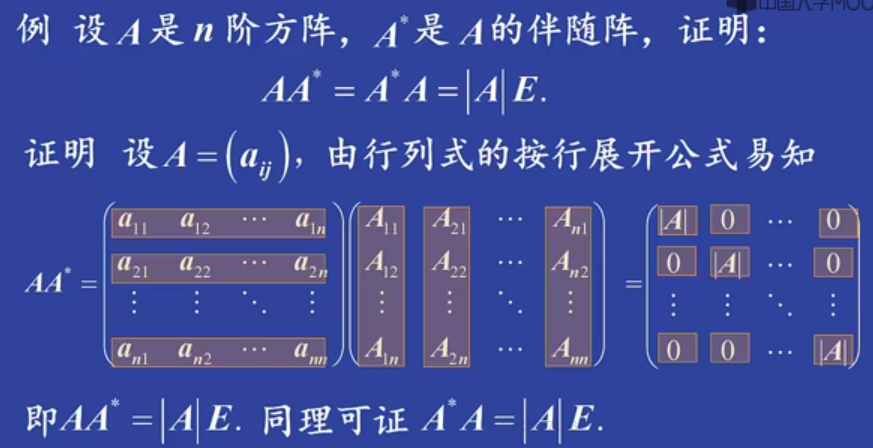
注意伴随矩阵,a12a_{12}a12的伴随矩阵A12A_{12}A12是在A*里面的2,1位置

上三角矩阵的伴随矩阵仍为上三角矩阵。





这里有一个细节的点是单位矩阵E∗A=A∗EE*A=A*EE∗A=A∗E,所以可以直接写4XXT4XX^T4XXT


这里D=∣AABEO∣D=\begin{vmatrix} A & AB \\ E & O \\ \end{vmatrix}D= AEABO 的原因并没有给出,可以通过列变换,第一列乘以B加到第二列,其中-E * B + B = O

注意伴随矩阵,a12a_{12}a12的伴随矩阵A12A_{12}A12是在A*里面的2,1位置

上三角矩阵的伴随矩阵仍为上三角矩阵。
