Trie树
Trie字符串统计
思路:
Trie:高效的存储和查找字符串集合的数据结构(字母或数字)
存储从根节点出发,每个单词存储字母,如果不存在就创建,如果存在就继续下一个字母,每个单词完结了记得在结尾打个标签意味着这是单词末尾,查找也很简单,看是否能找到完整字符串并且结尾有标签。如下图所示
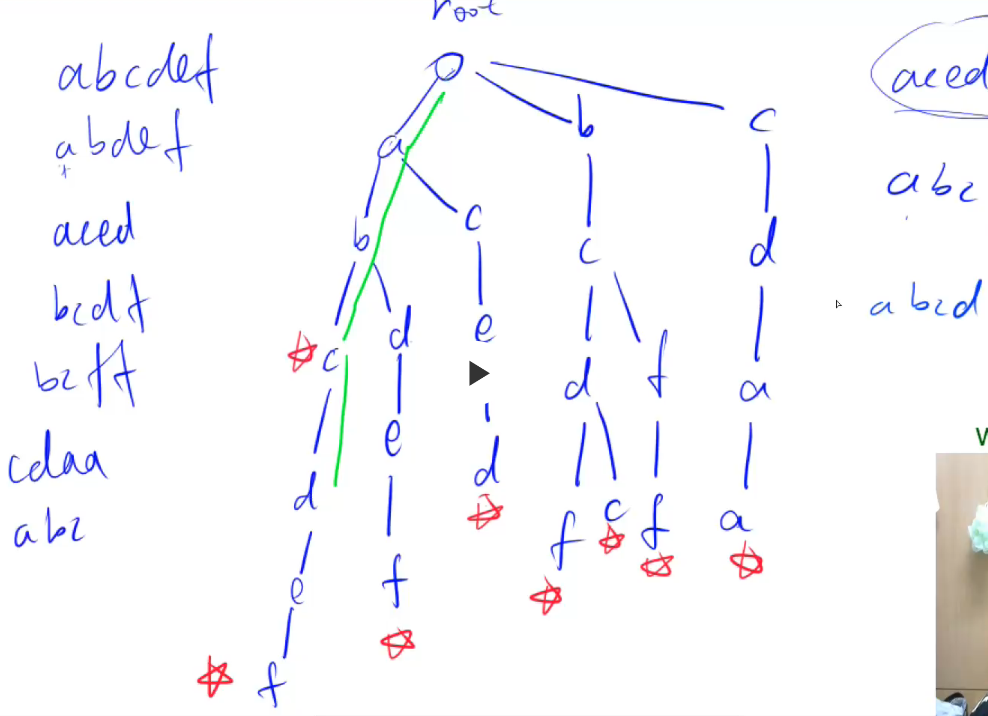
存储结构:int son[N][26],cnt[N],idx;//son[i][j]表示当前下标为i时字母j的子节点cnt是用来存储结尾单词的数量的,下标为0的点即是根节点也是空节点 idx是树的层数
演示案例:
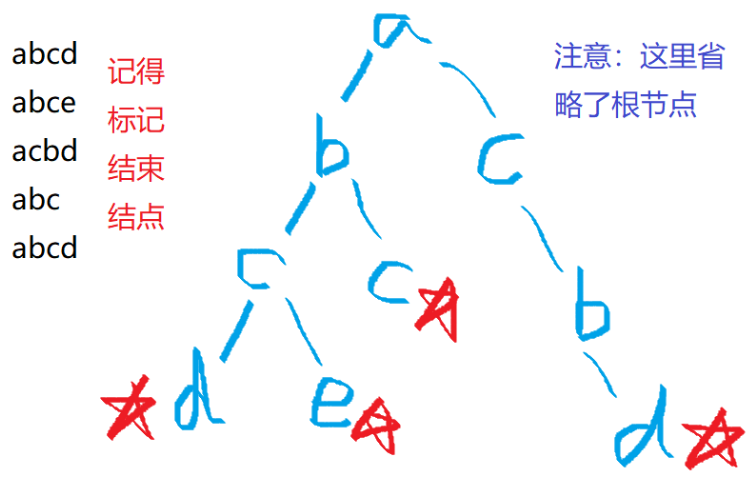
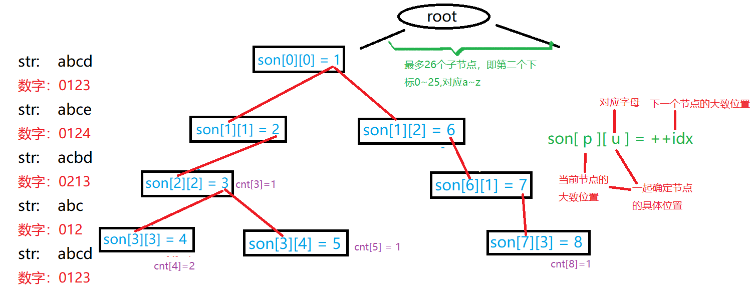
代码:
java
import java.util.*;
public class Main{
static int N = 100010,idx = 0;
static int[][] son = new int[N][26];
static int[] cnt = new int[N];
static char[] str = new char[N];
public static void insert(char[] str){
int p = 0; //下标0表示头结点,根节点
for(int i = 0 ; i < str.length; i ++ ){
// 将字符串每个字符都转化成数字;0-25
int u = str[i] - 'a';
//如果这个的儿子分支没有字符,说明这条分支还没有这个字符插入过
//就新建一个然后赋值为然后把【idx】下标赋值上去,作为每个分支的专属坐标
if(son[p][u] == 0) son[p][u] = ++idx;
//然后将p往下前进一层
p = son[p][u];
}
//最后停在那一层的那个数字就做标记,说明这是一个字符串的结束。
cnt[p]++;
}
public static int query(char[] str){
int p = 0;//从根节点开始,下标是0表示根节点,头结点
for(int i = 0 ; i < str.length; i ++){
int u = str[i] - 'a'; // 将字符串每个字符都转化成数字0-25
//如果这个点上面没有标记,就说明没有存入过这个字符,所以返回0
if(son[p][u] == 0) return 0;
//如果这个点上面能寻找到这个字符,就让他往下一层继续寻找;
p = son[p][u];
}
//最后查找完之后输出最后一个做标记的点为下标的cnt数组的值。
return cnt[p];
}
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
String sss = scan.nextLine();
while(n -- > 0){
String s = scan.nextLine();
String[] st = s.split(" ");
String s1 = st[0];
String s2 = st[1];
if(s1.equals("I")){
insert(s2.toCharArray());
}else{
System.out.println(query(s2.toCharArray()));
}
}
}
}最大异或对
思路
将每个数以二进制方式存入Trie树,找的时候从当前数字最高位去找尽量和该位的相反的点,直到当前数字遍历到最低位,此时通过贪心思想得到的就是和当前数字异或最大的数,把所有数字都找一遍求个max就行。
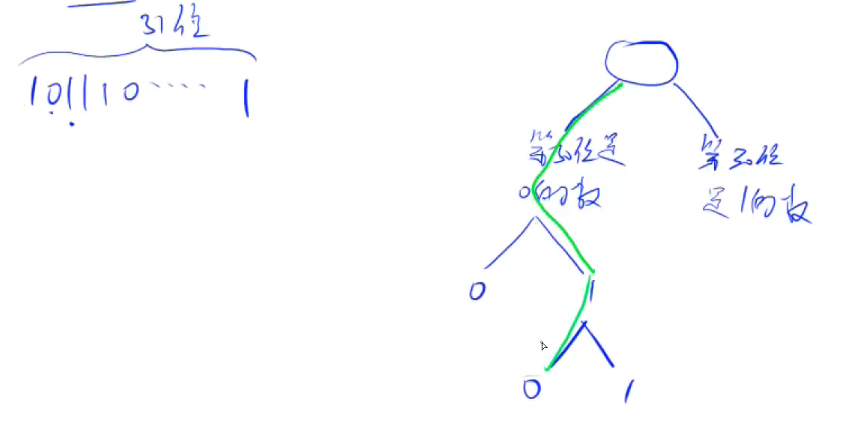

代码
java
import java.io.*;
public class Main{
static int N = 3100010,idx = 0;
static int[][] son = new int[N][2];
//插入
public static void add(int x){
int p = 0;//从头结点开始
for(int i = 30 ; i >= 0 ; i -- ){ //因为每一个数的二进制是有31位组成,所以需要从大开始遍历
int u = x >> i & 1;//每一个数的二进制31个二进制每一位看0还是1
if(son[p][u] == 0) son[p][u] = ++idx;//判断这一层是空的,就创建,然后赋值下标
p = son[p][u];//然后让往下前进一层
}
}
//查询
public static int query(int x){
int p = 0,res = 0;//从根节点0开始。res进就算异或后的最大值
for(int i = 30; i>= 0 ; i --){
int u = x >> i & 1;
if(son[p][1-u] != 0){ //如果该节点的u是0,则判断一下在这一层有没有跟他相反的0-1,1-0,如果相反对应位置有数
res += (1 << i);//res就将该二进制位对应异或之后的最优解1每一位顺次加起来。因为是异或相反数就是1,这是最优解
p = son[p][1-u];//然后往最优解那边前进一层。
}else{//否则就不是最优解的0匹配1,1匹配0,所以就异或之后的值是0
//res += (0 << i);因为是0所以可以省略,
p = son[p][u];//然后让他往不优解那边前进一层。
}
}
return res;//最后返回异或之后的最大值res
}
public static void main(String[] args)throws IOException{
BufferedReader re = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter wt = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(re.readLine());
String[] s = re.readLine().split(" ");
for(int i = 0 ; i < n ; i ++ ){
add(Integer.parseInt(s[i]));
}
int res = 0;
for(int i = 0 ; i < n ; i ++ ){
//因为输入的是字符串所以需要转成整形。然后每一次比较res的值谁大,然后将最大值重新赋值给res
res = Math.max(res,query(Integer.parseInt(s[i])));
}
wt.write(res +" ");//最后输出res,因为快输出输出的是字符串,所以需要在后面加上" ";
wt.close();
}
}