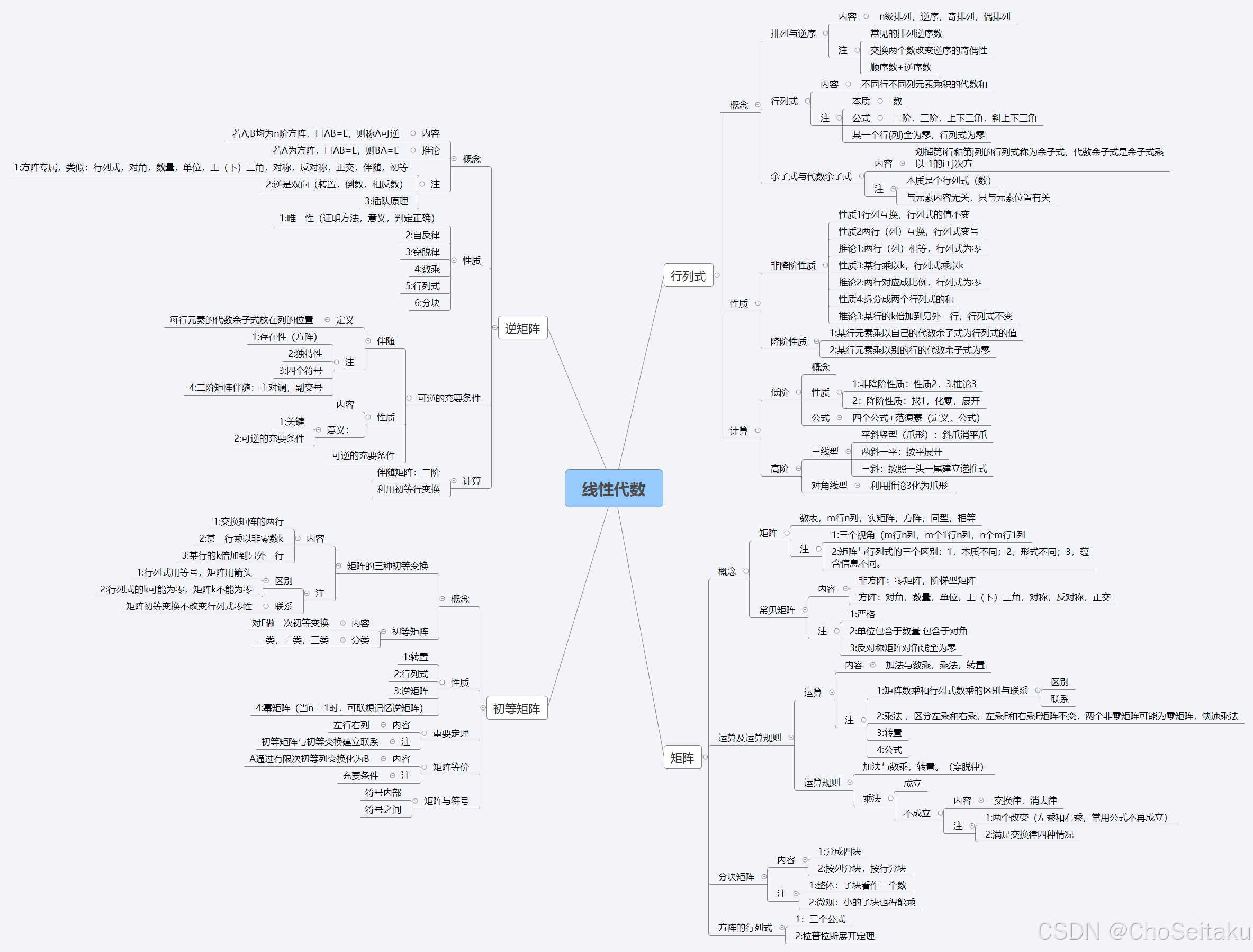
行列式
概念
- 排列与逆序
- 内容:n 级排列,逆序,奇排列,偶排列;
- 注:
- 常见的排列逆序数;
- 交换两个数改变逆序的奇偶性;
- 顺序数 + 逆序数=Cn2=n(n−1)2=C_n^2 = \frac{n(n-1)}{2}=Cn2=2n(n−1)
- 行列式
- 内容:不同行不同列元素乘积的代数和
- 注:
- 本质:数
- 公式(二阶,三阶,上下三角,斜上下三角);
- 某一个行 (列) 全为零,行列式为零
- 余子式与代数余子式
- 内容:划掉第 i 行和第 j 列的行列式称为余子式,代数余子式Aij=(−1)i+jMijA_{ij} = (-1)^{i+j} M_{ij}Aij=(−1)i+jMij
- 注:
- 本质:是个行列式(数)
- 与元素内容无关,只与元素位置有关
- Mij=(−1)i+jAijM_{ij} = (-1)^{i+j} A_{ij}Mij=(−1)i+jAij
- 推导:(−1)i+jAij=(−1)i+j(−1)i+jMij=((−1)2)i+jMij(-1)^{i+j} A_{ij} = (-1)^{i+j} (-1)^{i+j} M_{ij} = ((-1)^2)^{i+j} M_{ij}(−1)i+jAij=(−1)i+j(−1)i+jMij=((−1)2)i+jMij
性质
- 非降阶性质
- 性质 1:行列互换,行列式的值不变
- 注:
- 行和列具有相同的地位,对行成立对列也成立
- 用到抽象型行列式中
- 性质 2:两行(列)互换,行列式变号
- 推论 1:两行(列)相等,行列式为零
- 性质 3:某行乘以 k,行列式乘以 k(k可为0)
- 注:
- 与矩阵数乘的区别与联系
- 矩阵初等行变换的区别与联系
- 推论 2:两行对应成比例,行列式为零
- 注:
- 推论2=推论1+性质3
- 性质 4:按某一行拆分成两个行列式的和
- 推论 3:某行的 k 值加到另外一行,行列式不变
- 降阶性质
- 1:某行元素乘以自己的代数余子式之和为行列式的值
- 2:某行元素乘以以别的行的代数余子式之和为零
计算
- 低阶(4阶及以下)
- 概念:二阶;3阶含字母且含0
- 性质:
- 非降阶性质:性质 2(互换),性质3(数乘),推论 3(倍加);
- 降阶性质:
- 内容:某行元素乘以自己的代数余子式
- 步骤:找 1,化零,展开
- 公式:
- 四个公式(2阶,2阶,上下三角,斜上下三角)
- 范德蒙
- 识别:首行为1,每列等比 ∣111123149∣=(2−1)(3−1)(3−2)=2\begin{vmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 4 & 9 \end{vmatrix} = (2-1)(3-1)(3-2) = 2 111124139 =(2−1)(3−1)(3−2)=2
- 公式
- 2种变形
- 破坏首行为1: ∣1231491827∣=2∣1131291427∣=2⋅3∣111123149∣=6⋅2=12\begin{vmatrix} 1 & 2 & 3 \\ 1 & 4 & 9 \\ 1 & 8 & 27 \end{vmatrix} = 2\begin{vmatrix} 1 & 1 & 3 \\ 1 & 2 & 9 \\ 1 & 4 & 27 \end{vmatrix} = 2 \cdot 3\begin{vmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 4 & 9 \end{vmatrix} = 6 \cdot 2 = 12 1112483927 =2 1111243927 =2⋅3 111124139 =6⋅2=12
- 首列是 1,但每行不是等比;每列是等比,但首行不是 1
- 破坏等比数列:
∣1111123x149x21827x3∣=1⋅(−1)1+4∣1231491827∣+x⋅(−1)2+4∣1111491827∣+x2⋅(−1)3+4∣1111231827∣+x3⋅(−1)4+4∣111123149∣ \begin{vmatrix} 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & x \\ 1 & 4 & 9 & x^2 \\ 1 & 8 & 27 & x^3 \end{vmatrix} = 1 \cdot (-1)^{1+4} \begin{vmatrix} 1 & 2 & 3 \\ 1 & 4 & 9 \\ 1 & 8 & 27 \end{vmatrix} + x \cdot (-1)^{2+4} \begin{vmatrix} 1 & 1 & 1 \\ 1 & 4 & 9 \\ 1 & 8 & 27 \end{vmatrix} + x^2 \cdot (-1)^{3+4} \begin{vmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 8 & 27 \end{vmatrix} + x^3 \cdot (-1)^{4+4} \begin{vmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 4 & 9 \end{vmatrix} 11111248139271xx2x3 =1⋅(−1)1+4 1112483927 +x⋅(−1)2+4 1111481927 +x2⋅(−1)3+4 1111281327 +x3⋅(−1)4+4 111124139
又
∣1111123x149x21827x3∣=(2−1)(3−1)(x−1)(3−2)(x−2)(x−3)=(x−1)(x−2)(x−3)⋅2=x3−12x2+⋯ \begin{vmatrix} 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & x \\ 1 & 4 & 9 & x^2 \\ 1 & 8 & 27 & x^3 \end{vmatrix} = (2-1)(3-1)(x-1)(3-2)(x-2)(x-3) \\ =(x-1)(x-2)(x-3) \cdot 2 \\ = x^3 - 12x^2 + \cdots 11111248139271xx2x3 =(2−1)(3−1)(x−1)(3−2)(x−2)(x−3)=(x−1)(x−2)(x−3)⋅2=x3−12x2+⋯
则
−∣1111231827∣=−12 -\begin{vmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 8 & 27 \end{vmatrix} = -12 − 1111281327 =−12
- 破坏首行为1: ∣1231491827∣=2∣1131291427∣=2⋅3∣111123149∣=6⋅2=12\begin{vmatrix} 1 & 2 & 3 \\ 1 & 4 & 9 \\ 1 & 8 & 27 \end{vmatrix} = 2\begin{vmatrix} 1 & 1 & 3 \\ 1 & 2 & 9 \\ 1 & 4 & 27 \end{vmatrix} = 2 \cdot 3\begin{vmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 4 & 9 \end{vmatrix} = 6 \cdot 2 = 12 1112483927 =2 1111243927 =2⋅3 111124139 =6⋅2=12
- 高阶
- 三线型:
- 平斜竖型(爪形):斜爪消平爪
- 两斜一平:按平展开;
- 三斜形:按照一头一尾建立递推式
- 对角线型:
- 定义:通过改变对角线元素的值使其成为每行元素对应成比例的行列式
- 计算:利用推论 3 (倍加)化为爪形
- 三线型:
矩阵
概念
- 数表,m 行 n 列,实矩阵,方阵,同型,相等
- 注:
- 三个视角(m 行 n 列,m 个 1 行 n 列,n 个 m 行 1 列);
- 矩阵与行列式的三个区别:
- 本质不同;
- 形式不同;
- 蕴含信息不同。
常见矩阵
- 非方阵:零矩阵,阶梯型矩阵,简单阶梯型
- 方阵:对角,数量,单位,上(下)三角,对称,反对称,正交
- 注:
- 严格单调递增;
- 单位包含于数量 包含于对角;
- 反对称矩阵对角线全为零
运算及运算规则
- 运算
- 内容:加法与数乘,乘法,转置
- 注:
- 矩阵数乘和行列式数乘的区别与联系(区别、联系)
- 乘法:
- 区分左乘和右乘,
- 左乘和右乘 E 矩阵不变,
- 两个非零矩阵相乘可能为零矩阵,
- 快速乘法
- 转置,3条
- 公式,
- AnA^nAn的两个公式
- 各行成比例
- 对角线元素相等的上(下)三角
- AnA^nAn的两个公式
- 运算规则
- 加法与数乘,转置,(穿脱律)
- 乘法
- 成立:内容(交换律,消去律)
- 不成立:
- 注:
- 两个改变(左乘和右乘,常用公式不再成立);
- 满足交换律四种情况
- 注:
分块矩阵
- 内容:
- 分成四块;
- 按列分块,按行分块
- 注:
- 整体:把每一个子块看作一个数;
- 微观:小的子块也得能乘
方阵的行列式
- 三个公式
∣AT∣=∣A∣,∣kA∣=kn∣A∣∣AB∣=∣A∣∣B∣ \begin{align*} |A^T| &= |A|, \quad |kA| = k^n |A| \\ |AB| &= |A||B| \end{align*} ∣AT∣∣AB∣=∣A∣,∣kA∣=kn∣A∣=∣A∣∣B∣ - 拉普拉斯展开定理
∣A00B∣=∣AC0B∣=∣A0CB∣=∣A∣∣B∣∣0AB0∣=∣0ABC∣=∣CAB0∣=(−1)m⋅n∣A∣∣B∣ \begin{align*} \begin{vmatrix} A & 0 \\ 0 & B \end{vmatrix} &= \begin{vmatrix} A & C \\ 0 & B \end{vmatrix} = \begin{vmatrix} A & 0 \\ C & B \end{vmatrix} = |A||B| \\ \begin{vmatrix} 0 & A \\ B & 0 \end{vmatrix} &= \begin{vmatrix} 0 & A \\ B & C \end{vmatrix} = \begin{vmatrix} C & A \\ B & 0 \end{vmatrix} = (-1)^{m \cdot n} |A||B| \end{align*} A00B 0BA0 = A0CB = AC0B =∣A∣∣B∣= 0BAC = CBA0 =(−1)m⋅n∣A∣∣B∣
逆矩阵
概念
- 内容:若 A,B 均为 n 阶方阵,且 AB=E,则称 A 可逆
- 推论:若 A 为n阶方阵,且 AB=E,则 BA=E
- 注:
- 方阵专属,类似:行列式,对角,数量,单位,上(下)三角,对称,反对称,正交,伴随,初等,特征值,相似,合同,正定
- 逆是双向(转置,倒数,相反数)
- 插队原理
ABCD=EABCDD−1=ED−1ABC=D−1DABC=DD−1=E \begin{align*} ABCD &= E \\ ABCDD^{-1} &= ED^{-1} \\ ABC &= D^{-1} \\ DABC &= DD^{-1} = E \end{align*} ABCDABCDD−1ABCDABC=E=ED−1=D−1=DD−1=E
性质
-
- 唯一性(证明方法,意义,判定正确)
-
- 自反性(A−1)−1=A(A^{-1})^{-1}=A(A−1)−1=A
-
- 穿脱律(AB)−1=B−1A−1, (A1A2⋯An)−1=An−1An−1−1⋯A1−1(AB)^{-1} = B^{-1}A^{-1},\ (A_1A_2\cdots A_n)^{-1} = A_n^{-1}A_{n-1}^{-1}\cdots A_1^{-1}(AB)−1=B−1A−1, (A1A2⋯An)−1=An−1An−1−1⋯A1−1
-
- 数乘(kA)−1=1kA−1 (k≠0)(kA)^{-1} = \frac{1}{k}A^{-1} \ (k \neq 0)(kA)−1=k1A−1 (k=0)
-
- 行列式∣A−1∣=1∣A∣|A^{-1}| = \frac{1}{|A|}∣A−1∣=∣A∣1
-
- 分块矩阵(A00B)−1=(A−100B−1),(0AB0)−1=(0B−1A−10)\begin{pmatrix} A & 0 \\ 0 & B \end{pmatrix}^{-1} = \begin{pmatrix} A^{-1} & 0 \\ 0 & B^{-1} \end{pmatrix},\begin{pmatrix}0 & A \\B & 0\end{pmatrix}^{-1}=\begin{pmatrix}0 & B^{-1} \\A^{-1} & 0\end{pmatrix}(A00B)−1=(A−100B−1),(0BA0)−1=(0A−1B−10)
可逆的充要条件
-
伴随
- 定义:每行元素的代数余子式放在列的位置
- 注:
- 存在性(方阵);
- 独特性;
- 四个符号(n,T,-1,
*); - 二阶矩阵伴随:主对调,副变号
-
性质
- 内容:AA∗=A∗A=∣A∣EAA^* = A^*A = |A|EAA∗=A∗A=∣A∣E
- 关键;
- 得出可逆的充要条件的关键
- 意义:可逆的充要条件 ∣A∣≠0 ⟺ A 可逆|A| \neq 0 \iff A \text{ 可逆}∣A∣=0⟺A 可逆
- 内容:AA∗=A∗A=∣A∣EAA^* = A^*A = |A|EAA∗=A∗A=∣A∣E
-
计算
- 伴随矩阵:二阶A−1=A∗∣A∣A^{-1} = \frac{A^*}{|A|}A−1=∣A∣A∗
- 利用初等行变换:(A∣E)→初等行变换(E∣A−1)(A \mid E) \xrightarrow{\text{初等行变换}} (E \mid A^{-1})(A∣E)初等行变换 (E∣A−1)
初等矩阵
概念
- 矩阵的三种初等变换
- 内容:
- 交换矩阵的两行;
- 某一行乘以非零数 k;
- 某行的 k 倍加到另外一行
- 注:
- 区别:
- 行列式用等号,矩阵用箭头;
- 行列式的 k 可能为零,矩阵 k 不能为零
- 联系:矩阵初等变换不改变行列式的零性
- 区别:
- 内容:
- 初等矩阵
- 分类:对E做一次初等变换
- 一类
- 二类
- 三类
- 性质:
- 转置;
- 行列式;
- 逆矩阵;
- 幂矩阵(当 n=1 时,可联想记忆逆矩阵)
- 重要定理:左行右列
- 注:初等矩阵与初等变换建立联系
- 分类:对E做一次初等变换
- 矩阵等价
- 内容:A 通过有限次初等列变换化为 B
- 充要条件:A 与 B 等价 ⟺ r(A)=r(B)A \text{ 与 } B \text{ 等价} \iff r(A) = r(B)A 与 B 等价⟺r(A)=r(B)
- 矩阵与符号
- 符号内部
行列式数乘自反性穿脱律T∣AT∣=∣A∣(kA)T=kAT(AT)T=A(AB)T=BTAT−1∣A−1∣=1∣A∣(kA)−1=1kA−1(A−1)−1=A(AB)−1=B−1A−1∗∣A∗∣=∣A∣n−1(kA)∗=kn−1A∗(A∗)∗=∣A∣n−2A(AB)∗=B∗A∗ \begin{array}{c|c|c|c|c} & \text{行列式} & \text{数乘} & \text{自反性} & \text{穿脱律} \\ \hline T & |A^T| = |A| & (kA)^T = kA^T & (A^T)^T = A & (AB)^T = B^T A^T \\ \hline -1 & |A^{-1}| = \frac{1}{|A|} & (kA)^{-1} = \frac{1}{k}A^{-1} & (A^{-1})^{-1} = A & (AB)^{-1} = B^{-1} A^{-1} \\ \hline* & |A^*| = |A|^{n-1} & (kA)^* = k^{n-1}A^* & (A^*)^* = |A|^{n-2}A & (AB)^* = B^* A^* \\ \hline \end{array} T−1∗行列式∣AT∣=∣A∣∣A−1∣=∣A∣1∣A∗∣=∣A∣n−1数乘(kA)T=kAT(kA)−1=k1A−1(kA)∗=kn−1A∗自反性(AT)T=A(A−1)−1=A(A∗)∗=∣A∣n−2A穿脱律(AB)T=BTAT(AB)−1=B−1A−1(AB)∗=B∗A∗
AA∗=∣A∣EA∗(A∗)∗=∣A∗∣E=∣A∣n−1E(A∗)∗=∣A∣n−1⋅(A∗)−1=∣A∣n−1⋅A∣A∣=∣A∣n−2A \begin{align*} AA^* &= |A|E \\ A^*(A^*)^* &= |A^*|E = |A|^{n-1}E \\ (A^*)^* &= |A|^{n-1} \cdot (A^*)^{-1} \\ &= |A|^{n-1} \cdot \frac{A}{|A|} = |A|^{n-2}A \end{align*} AA∗A∗(A∗)∗(A∗)∗=∣A∣E=∣A∗∣E=∣A∣n−1E=∣A∣n−1⋅(A∗)−1=∣A∣n−1⋅∣A∣A=∣A∣n−2A
- 符号之间:两两可交换位置