P1477 [NOI2008] 假面舞会 - 洛谷 (luogu.com.cn)
几乎所有题解都把这题复杂化了,但实际上很好想。
题面中 "栋栋收集的信息不能保证其完整性",即整张图不一定联通,
是一个多个弱连通分量的非弱连通有向图。
非弱连通有向图中的每一个弱联通分量 ,我们都找一个点(当作 1 号面具)开始遍历,目标是给每个点都标上编号。
但弱连通分量 内部不一定是强联通(任意两个点都能互相到达)的,即可能出现这种情况:
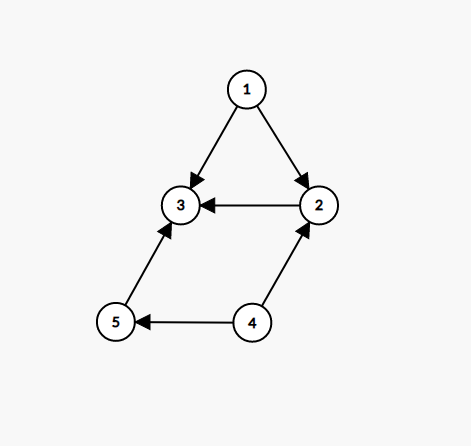
如果我们不幸的选择了 3 开始,那将寸步难行。
为了让整个分量强连通,我们可以建双向边。
即原来 5 - > 3(边权为 1)代表 3 的面具等级比 5 大一层,再建 3 -> 5(边权为 -1)还是代表 3 的面具等级比 5 大一层,但从 3 出发也可以到 5 了,整体相对层级差还是不变。
这是很重要的,我们必须保证(原先的)弱连通分量内部是强连通的,才方便下一步操作。
(如果一个分量内部要多次 dfs 统计层数的话(不是强连通),不同次的 dfs 之间产生的层数结果会冲突,可以自己试一下)
如果单个连通分量 内部有长度为 的环,则
。
因为 里面必须包括至少一对
和
,并且
还得是
的倍数,才能完美的连成一个环。
我们只要遍历到有点被遍历过,把新层级和旧层级一减,得到的就是环的大小。
注意是所有树的所有环 都满足 ,即
。
(可以自己想一下如果有一个环不满足的情况,那就根本不可能连成环!)
(如果 最后小于 3,无解。反之最大就是最大公约数本身,最小是
大于 3 的最小约数)
如果整个图 都没有环(连通分量都是树),那么 就很自由了。
可以直接等于 单个树里面最大层级 - 最小层级的差 + 1 的和,也可以等于 3。
(因为单个树里面 最大层级 - 最小层级的差 + 1 就是这棵树里面最长链的大小,链多大就是面具层级(总种类)有多大。树之间互不重合,可以当作是完全不同的面具层级)
(当然如果这些 差 的和还小于 3,直接输出无解)
代码:
cpp
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
const int M = 1e6 + 10;
vector<PII> G[N];
int n, m;
int d[N], mnd, mxd; bool v[N];
int ans_cycle, ans_chain;
void update(int &a, int b) {
if (a == 0) {
a = b;
}
else {
a = __gcd(a, b);
}
}
void dfs(int x) {
v[x] = 1;
mnd = min(d[x], mnd);
mxd = max(d[x], mxd);
for (auto i : G[x]) {
int y = i.first, w = i.second;
if (!v[y]) {
d[y] = d[x] + w;
dfs(y);
}
else {
update(ans_cycle, abs(d[x] + w - d[y]));
}
}
}
int main () {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= m; i ++) {
int x, y;
cin >> x >> y;
G[x].push_back({y, 1});
G[y].push_back({x, -1});
}
ans_cycle = 0, ans_chain = 0;
memset(v, 0, sizeof(v));
for (int i = 1; i <= n; i ++) if (!v[i]) { // 新的弱联通分量
d[i] = 1;
mnd = 1e9; mxd = 0;
dfs(i);
ans_chain += (mxd - mnd + 1);
}
if (ans_cycle) { // 有至少一个环
if (ans_cycle < 3) {
cout << "-1 -1\n";
}
else {
for (int i = 3; i <= ans_cycle; i ++) if (ans_cycle % i == 0) {
cout << ans_cycle << " " << i << "\n";
break;
}
}
}
else { // 没环
if (ans_chain < 3) {
cout << "-1 -1\n";
}
else {
cout << ans_chain << " " << "3\n";
}
}
return 0;
}