一、实验题目
5.18零钱兑换2
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
673.最长递增子序列的个数
给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。
注意 这个数列必须是 严格 递增的。
1143.最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
583.两个字符串的删除操作
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。
712.两个字符串的最小ASCII删除和
给定两个字符串s1 和 s2,返回 使两个字符串相等所需删除字符的 ASCII 值的最小和 。
二、实验思路和方案
5.18零钱兑换2
采用动态规划。我们定义一个一维数组 dp 来表示组成各个金额的硬币组合数。对于每个硬币面额,我们遍历金额从该硬币面额开始到总金额,更新组合数。最终返回 dp[amount] 即可得到总金额的组合数量。
673.最长递增子序列的个数
dp[i] 表示以 nums[i] 为结尾的最长递增子序列的长度,看比 nums[i] 小的数能不能转移过来即可,记录其中能转移的最大长度。由于这题求最长递增子序列的个数,所以还要针对每一个长度记录其数量。因此,我们可以再额外声明一个记录数量的数组 count[i] 表示以 nums[i] 结尾的最长递增子序列的长度。
1143.最长公共子序列
定义 f[i][j]表示字符串text1的[1,i]区间和字符串text2的[1,j]区间的最长公共子序列长度(注意:下标从1开始)。状态转移方程为:
f[i][j] = f[i-1][j-1] + 1 ,当text1[i] == text2[j]
f[i][j] = max(f[i - 1][j],f[i][j - 1]),当text1[i] != text2[j]
583.两个字符串的删除操作
给定两个字符串 word 1和 word 2,分别删除若干字符之后使得两个字符串相同,则剩下的字符为两个字符串的公共子序列。为了使删除操作的次数最少,剩下的字符应尽可能多。当剩下的字符为两个字符串的最长公共子序列时,删除操作的次数最少。因此,可以计算两个字符串的最长公共子序列的长度,然后分别计算两个字符串的长度和最长公共子序列的长度之差,即为两个字符串分别需要删除的字符数,两个字符串各自需要删除的字符数之和即为最少的删除操作的总次数。
712.两个字符串的最小ASCII删除和
假设字符串s1和s2的长度分别为 m 和 n,创建 m+1 行 n+1 列的二维数组 dp,其中dp[i][j] 表示使s1[0:i]和s2[0:j] 相同的最小ASCII删除和。
得到状态转移方程后计算得到 dp[m][n] 即为使s1和s2相同的最小 ASCII 删除和。
三、实验代码
5.18零钱兑换2
class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] += dp[i - coin];
}
}
return dp[amount];
}
}673.最长递增子序列的个数
class Solution {
public int findNumberOfLIS(int[] nums) {
int n = nums.length;
int maxLen = 1;
int ans = 1;
int[] dp = new int[n];
int[] count = new int[n];
dp[0] = count[0] = 1;
for (int i = 1; i < n; i++) {
dp[i] = count[i] = 1;
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i]) {
if (dp[j] + 1 > dp[i]) {
dp[i] = dp[j] + 1;
count[i] = count[j];
} else if (dp[j] + 1 == dp[i]) {
count[i] += count[j];
}
}
}
if (dp[i] > maxLen) {
maxLen = dp[i];
ans = count[i];
} else if (dp[i] == maxLen) {
ans += count[i];
}
}
return ans;
}
}1143.最长公共子序列
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int n = text1.length(), m = text2.length();
int[][] f = new int[n + 1][m + 1];
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
f[i][j] = f[i - 1][j - 1] + 1;
} else {
f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);
}
}
}
return f[n][m];
}
}583.两个字符串的删除操作
class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
char c1 = word1.charAt(i - 1);
for (int j = 1; j <= n; j++) {
char c2 = word2.charAt(j - 1);
if (c1 == c2) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
int lcs = dp[m][n];
return m - lcs + n - lcs;
}
}712.两个字符串的最小ASCII删除和
class Solution {
public int minimumDeleteSum(String s1, String s2) {
int m = s1.length(), n = s2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
dp[i][0] = dp[i - 1][0] + s1.codePointAt(i - 1);
}
for (int j = 1; j <= n; j++) {
dp[0][j] = dp[0][j - 1] + s2.codePointAt(j - 1);
}
for (int i = 1; i <= m; i++) {
int code1 = s1.codePointAt(i - 1);
for (int j = 1; j <= n; j++) {
int code2 = s2.codePointAt(j - 1);
if (code1 == code2) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(dp[i - 1][j] + code1, dp[i][j - 1] + code2);
}
}
}
return dp[m][n];
}
}四、实验结果及分析
5.18零钱兑换2
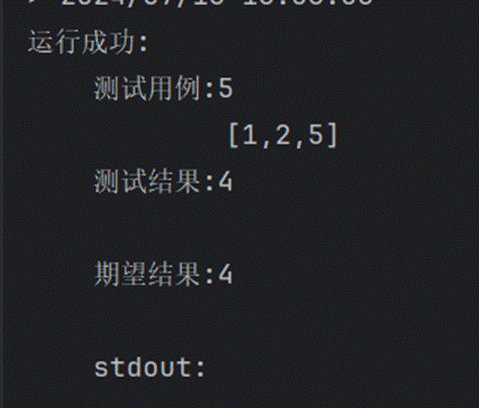
673.最长递增子序列的个数
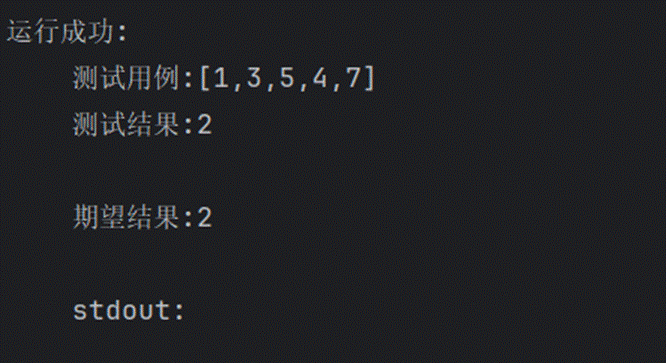
1143.最长公共子序列

583.两个字符串的删除操作
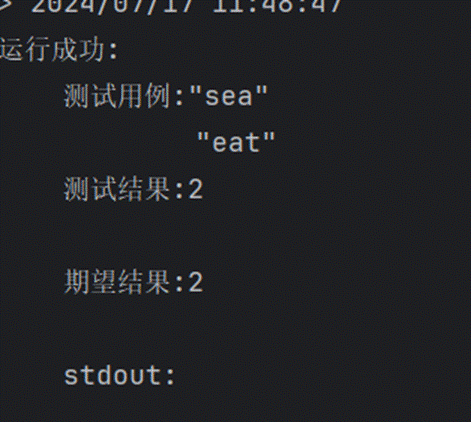
712.两个字符串的最小ASCII删除和

五、实验总结及体会
动态规划------子序列问题实验让我深刻理解了动态规划的思想与应用。通过本次课程与实验,我了解了有关状态定义、状态转移方程和边界条件的知识。在实验过程中,我体会到了动态规划的优化子问题重叠计算、减少时间复杂度的强大能力,并且学会了更多有关动态规划的技巧方法。