什么是"预测速度场 vtv_tvt = ε\varepsilonε - x\mathbf{x}x?
要理解这个,我们需要先了解传统扩散模型在做什么,然后看这篇论文用的新方法(Flow Matching)有什么不同。
1. 传统扩散模型(DDPM):预测噪声
在经典的扩散模型中,我们定义一个"前向过程",逐步向一张图片 (x(\mathbf{x}(x) 添加高斯噪声,经过很多步后,图片会变成纯粹的噪声 (ε(\mathbf{\varepsilon}(ε)。(即,扩散过程往往是固定的,即采用一个预先定义好的variance schedule,比如DDPM就采用一个线性的variance schedule。)
- 在训练时,模型看到的是一个部分噪声化的图片 (xt(\mathbf{x}_t(xt)。
- 模型的学习目标 是:预测出我们当初加入的噪声 (ε(\mathbf{\varepsilon}(ε)。
- 输出 :预测的噪声 (εθ(\mathbf{\varepsilon}_{\theta}(εθ)。
2. 本文采用的Flow Matching方法:预测速度场
本文使用了更现代的Flow Matching 目标。它采用了一个更直观的"线性插值"作为前向过程:
xt=(1−t)x+tε\mathbf{x}_t = (1-t) \mathbf{x} + t \mathbf{\varepsilon}xt=(1−t)x+tε
这里:
- (t=0(t=0(t=0) 时,(x0=x(\mathbf{x}_0 = \mathbf{x}(x0=x),是干净的图片(在潜在空间中)。
- (t=1(t=1(t=1) 时,(x1=ε(\mathbf{x}_1 = \mathbf{\varepsilon}(x1=ε),是纯粹的噪声。
- (t=0.5(t=0.5(t=0.5) 时,(x0.5(\mathbf{x}_{0.5}(x0.5) 就是一半图片、一半噪声的混合体。
这个公式对时间 (t(t(t) 求导,就得到了 "速度":
dxtdt=ε−x\frac{d\mathbf{x}_t}{dt} = \mathbf{\varepsilon} - \mathbf{x}dtdxt=ε−x
这个速度 ((ε−x)((\mathbf{\varepsilon} - \mathbf{x})((ε−x)) 的方向,正好指明了如何从噪声 (ε(\mathbf{\varepsilon}(ε) 一步"流回"到干净图片 (x(\mathbf{x}(x)。
所以,模型的输出是"预测速度场 (vt( v_t(vt = ε\varepsilonε - x\mathbf{x}x)" 意味着:
- 模型的学习目标 不再是预测噪声,而是学习这个方向场 。它告诉模型:"在当前的噪声水平 (t(t(t) 下,为了回到干净图片,你应该朝哪个方向移动"。
- 这被认为是一种更高效、更直接的学习信号,因此通常能带来更快的收敛速度(这也是本文强调的一个优势)。
注意FM与DDPM前向区别:
1. 传统扩散模型(DDPM)的前向过程:多次小量加噪
这是一个马尔可夫链过程,每一步都加入一点新的噪声:
xt=αtxt−1+1−αtεt\mathbf{x}t = \sqrt{\alpha_t} \mathbf{x}{t-1} + \sqrt{1-\alpha_t} \varepsilon_txt=αt xt−1+1−αt εt
其中,(εt∼N(0,I)( \varepsilon_t \sim \mathcal{N}(0, \mathbf{I})(εt∼N(0,I)) 是每一步新采样的独立噪声。
- 特点 :从 (x0( \mathbf{x}_0(x0) 到 (xT( \mathbf{x}_T(xT) 需要很多步(如1000步),每一步都有一个独立的 (εt( \varepsilon_t(εt)。
- 最终状态 (xT( \mathbf{x}_T(xT) 是所有这些噪声累积的结果,近似于标准高斯分布。
但DDPM的前向过程不是一个需要预计算并存储的"视频",而是一个可以由数学公式随时、随地重新生成的"配方" 。过程如下:
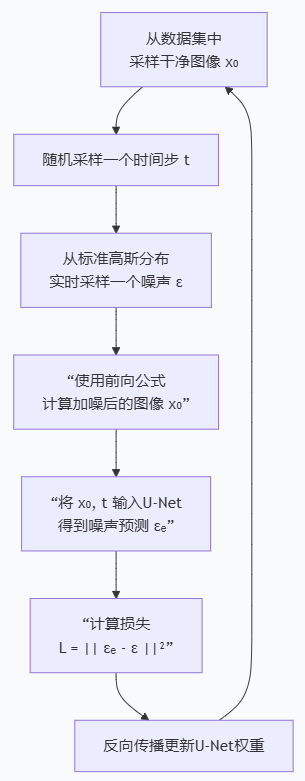
这个循环的关键在于第3步:对于每一个训练样本(x₀x_₀x₀),在每一个随机时间步(ttt),我们都会实时地从一个标准高斯分布中重新采样一个全新的、独立的噪声(εεε)。
2. Flow Matching(本文方法)的前向过程:一次性大量加噪,然后线性插值
这是一个非马尔可夫的、直接的过程:
-
准备起点和终点:
- 起点:干净数据 (x∼p(x)(\mathbf{x} \sim p(\mathbf{x})(x∼p(x)) (在RAE的潜在空间中)
- 终点:一次性采样 的纯噪声(ε∼N(0,I)( \varepsilon \sim \mathcal{N}(0, \mathbf{I})(ε∼N(0,I))
-
构建直线路径 :
在起点和终点之间进行线性插值 ,从而定义出中间状态 ( \mathbf{x}_t ):
xt=(1−t)x+tε,t∈[0,1]\mathbf{x}_t = (1-t) \mathbf{x} + t \varepsilon, \quad t \in [0, 1]xt=(1−t)x+tε,t∈[0,1]
关键区别在于:
- 对于每一张训练样本 (x( \mathbf{x}(x),我们只为其采样一个 噪声向量 (ε( \varepsilon(ε)。
- 这个 (ε( \varepsilon(ε) 在整个关于这张图的训练过程中(对于所有 (t( t(t) )都是固定不变的。
- 时间 (t( t(t) 在这里不再代表"第几步",而是代表"沿着这条直线路径走了多远的比例"。
t=0是起点(干净数据),t=1是终点(纯噪声)。
为什么要强调"ODE采样逐步去噪"?
这涉及到两种不同的"反向过程"数学形式:SDE(随机微分方程)和 ODE(常微分方程)。
1. SDE(随机微分方程)采样
- 这是早期扩散模型常用的方法。
- 在从噪声生成图片的每一步中,除了按照确定性的方向(漂移项)走,还会注入一些随机噪声(扩散项)。
- 优点:理论上能生成更多样化的样本。
- 缺点 :采样速度慢,通常需要很多步(如1000步)才能得到好结果,因为过程是随机的。
2. ODE(常微分方程)采样
- 这是Flow Matching等方法对应的采样方式。
- 它定义了一个完全确定性的过程。一旦起点(噪声)确定,生成的路径和终点(图片)就是唯一的。
- 优点 :
- 采样速度快:可以用更少的步数(如本文用的50步,甚至更少)生成高质量图片。
- 兼容高性能ODE求解器:可以利用像Euler(欧拉法)、Heun等数值积分方法,高效地从噪声"积分"回图片。
- 过程稳定、可逆。
为什么本文要强调"ODE采样"?
因为本文的核心贡献之一是让Diffusion Transformer在高维的RAE潜在空间 中也能高效、稳定地训练和生成。
- 使用ODE采样 是实现其**"高效"** 和 "实用" 主张的关键一环。
- 它证明了他们的方法(RAE + DiT-DH + Flow Matching)可以形成一个顺畅的、确定性的生成管道,从而快速地产出高质量图片。
- 这颠覆了"高维潜在空间中扩散训练困难"的传统观念,展示了其可行性。
简单总结:
- 强调ODE采样,是在强调他们方法的"高效性"和"确定性"。这意味着更快的生成速度、更少的计算资源,以及更适合部署的特性,这都是相比于早期扩散模型的巨大优势。
总结
- 输出速度场 :是本文采用的Flow Matching 技术的核心,模型学习的是一个从噪声指向干净数据的方向向量,这被认为比传统"预测噪声"的目标更高效。
- 强调ODE采样 :是为了突出其生成过程的确定性和高效性,可以使用更少的步骤快速生成高质量图片,这是该方法实用化的关键。