------《The model predictive control strategy of the transcritical CO₂ air conditioning system used in railway vehicles》
Zhang Teng, Feng Cao, Yulong Song†, Jiahang Ren, Gang Bai, Xuebo Pang, Yaling He Applied Thermal Engineering, 2023, 218: 119376
一、研究背景与动机
随着全球碳中和目标推进,铁路车辆热管理面临双重挑战:
环保法规:传统 HFCs 制冷剂被禁用,根据《蒙特利尔议定书》基加利修正案(2016年通过),发达国家自2019年起逐步削减HFCs,到2040年代减少80-85%;发展中国家自2024年起冻结生产,并逐步禁用GWP值高于2500的HFCs。需采用零 ODP、低 GWP 的天然工质 CO₂。
宽工况运行 :高铁环境温度、乘客负载、列车速度剧烈变化,传统控制难以兼顾能效 与舒适性。
核心矛盾:
传统经验公式仅优化排气压力 → 局部最优。
忽略蒸发器空气体积流量(EAVFR,简称qv)、压缩机转速与舱温耦合 → 能效损失、舒适性波动。例如,某高铁在夏季高温(40℃)、满载(80人)工况下,采用传统PID控制时,舱温波动达±2℃,COP较理论最大值低12%。
本文目标:提出多变量模型预测控制(MPC)策略,实现排气压力 + 蒸发器空气体积流量 + 压缩机转速 的全局协同优化,在保证乘客舒适前提下最大化系统 COP。为解决上述传统控制的局限性,本文首先亮出核心创新点与实际意义,继而详述方法与验证。
二、核心创新点(vs 传统控制)
|------|----------------|------------------------------------|
| | 传统控制(经验公式+PID) | MPC控制策略 |
| 优化变量 | 单变量(仅排气压力 pd) | 多变量(pd + qv + 压缩机转速 N) |
| 决策依据 | 离线标定公式 | 在线预测模型 + 滚动优化 |
| 优化目标 | 局部最优 | 全局最优(COP 最大 + 舒适稳定,平均 COP 提升 7.4%) |
三、研究方法
|-------|----------------|-------------|--------|
| 模块 | 输入参数 | 输出参数 | 建模方式 |
| 制冷单元 | 环境温度、送风温度、排气压力 | 制冷系数COP_r | BP神经网络 |
| 压缩机功耗 | 压缩机转速 | 压缩机功耗W_comp | 稳态线性化 |
| 冷量输出 | W_comp、COP_r | 制冷量Q_cool | 热力学计算 |
| 舱室动态 | 通风、透热、人体散热 | 舱温变化 | 物理热平衡 |
3.1 系统组成与信号
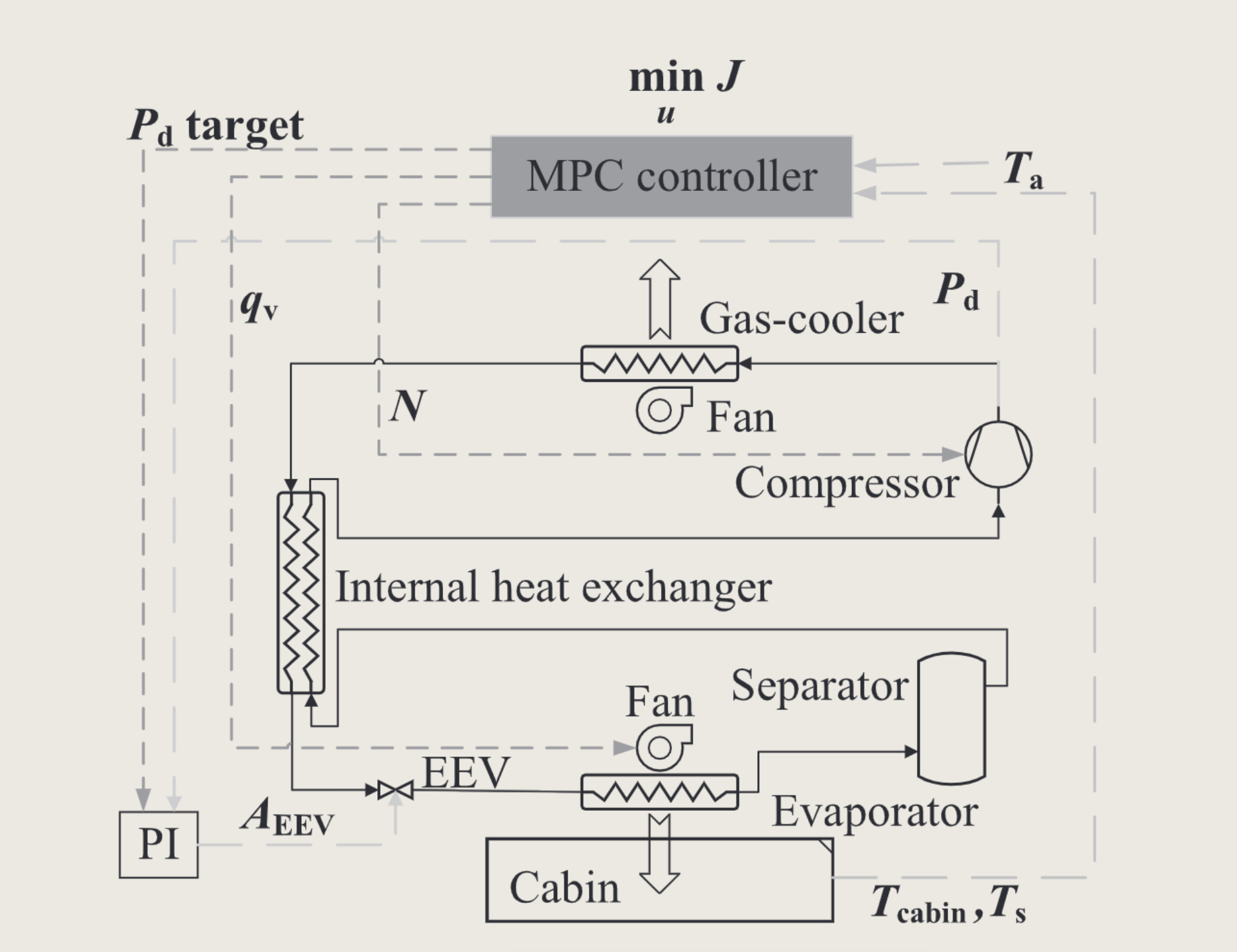
系统包括压缩机、气冷器、蒸发器、内部换热器(IHX)、电子膨胀阀(EEV)、分离器、离心风机与车厢热模型。
控制输入:u=[ N, qv, pd ]T(压缩机转速、蒸发器空气体积流量、排气压力)。
状态/输出:送风温度 ts、车厢温度 tc,以及能耗量 Wcomp、Wfan、制冷量 Qcool、能效 COPr。
扰动:d=[ ta, Qrad, vt, n ]T(环境温度、太阳辐射、列车速度、乘客数)。
舒适约束:tc∈[tc,min, tc,max](不建模湿度)。
3.2 控制目标
在预测时域内,维持舱温舒适的同时最小化能耗/最大化能效,并限制执行器幅值与变化率。
3.3 灰箱模型
3.3.1 数据驱动子模型
跨临界能效对 呈近似单峰且受
、
显著影响。构建 BP-NN:
训练数据来自台架/高保真仿真(如 GT-SUITE)在可行域的 DOE 采样。为保证物理一致性,在训练中施加:
-
正性约束:COP_r>0(输出激活或罚项);
-
单峰/平滑先验(对 p_d 方向的二阶差分惩罚);
-
边界趋势先验(高 t_a 时 p_d⋆ 上移的软约束);
-
可行域屏蔽:对 (t_a,t_s,p_d) 的非法组合加大损失或剔除。
3.3.2 执行器功率与制冷量
压缩机与风机功率模型:
压缩机功:
风机功:
制冷量由能效与功耗耦合得到:
3.3.3 送风--舱室热耦合
空气侧换热近似:
变换得:
考虑换热与执行器滞后,给送风温一阶惯性:
车厢热平衡:
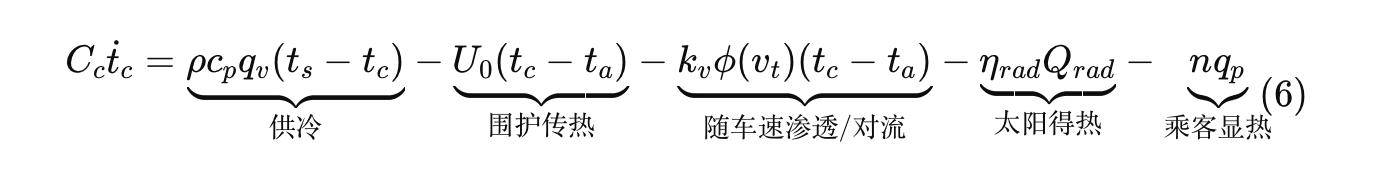
离散化(显式欧拉):
3.3.4 模型集成与可微性
离散灰箱预测器:
其中 x=[ts,tc]T。BP-NN 的可微性使得 ∇f,∇g 可由自动微分获得;若采用二次规划求解器,可对 f,g 在工作点局部线性化(SCP):
3.4.5 灰箱结构图解
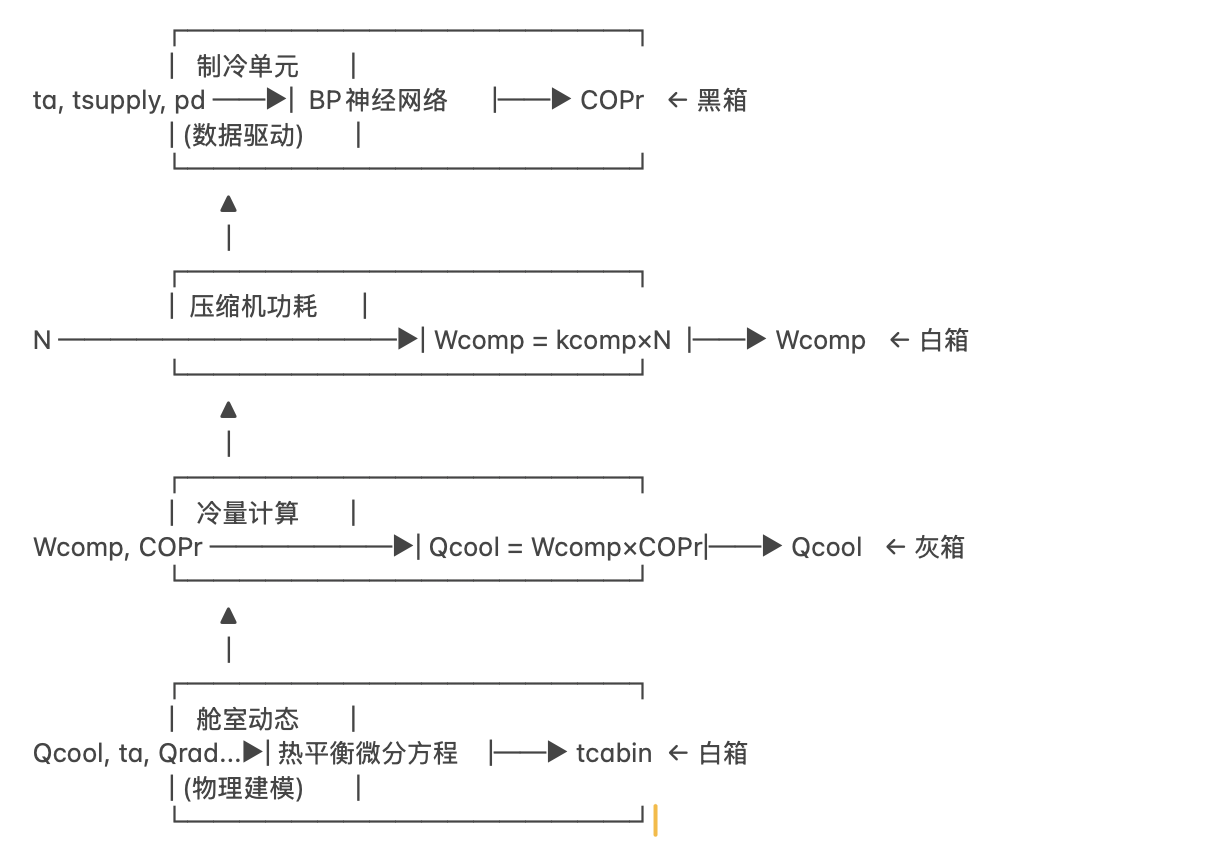
3.4 MPC 问题表述
3.4.1 目标函数
在预测时域 Np 与控制时域 Nc 内优化:
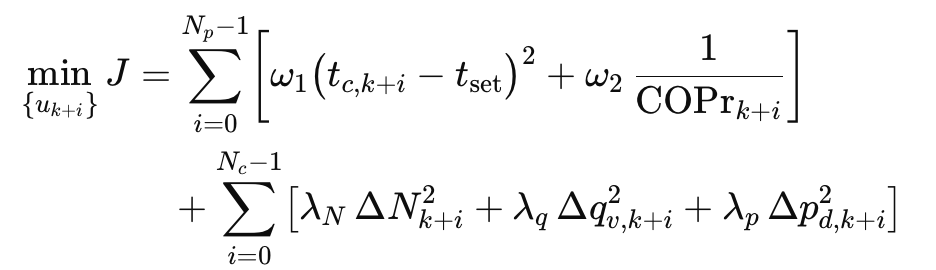
3.4.2 约束
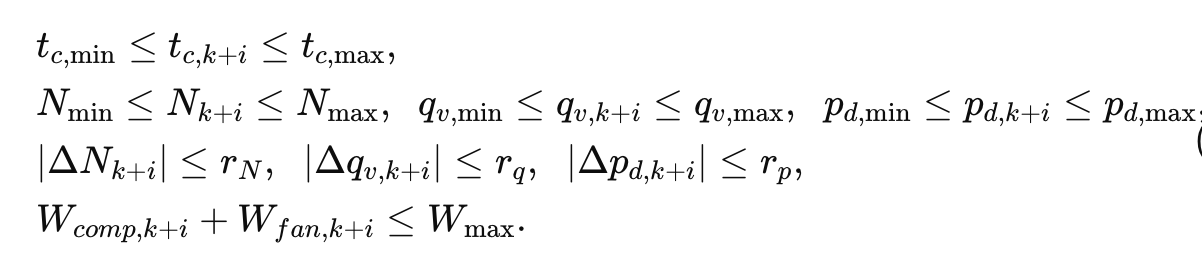
3.5 符号表(部分)
| 符号 | 含义 | 单位 |
|---|---|---|
| ta | 环境温度 | °C |
| ts | 送风温度 | °C |
| tc | 车厢温度 | °C |
| pd | 排气压力(高侧) | MPa |
| N | 压缩机转速 | r/min |
| qv | 蒸发器空气体积流量 | m³/s |
| Wcomp | 压缩机功率 | kW |
| Wfan | 风机功率 | kW |
| Qcool | 制冷量 | kW |
| COPr | 制冷模式能效(COP) | -- |
| Cc | 车厢等效热容 | kJ/K |
| U0 | 围护传热系数 | kW/K |
| kv | 渗透/随速换热系数 | kW/K |
| ηrad | 太阳得热折减系数 | -- |
| ρ,cp | 空气密度/定压比热 | kg/m³,kJ/(kg·K) |
| τs | 送风一阶时间常数 | s |
4.代码
import numpy as np
def sigmoid(x):
"""Sigmoid激活函数,如Eq. (23)中定义。"""
return 1 / (1 + np.exp(-x))
def predict_COPr(ta, tsupply, pd, wij, b1, wjm, b2):
"""
使用BP神经网络预测制冷单元性能系数COPr。
参数:
- ta: 环境温度 (°C)
- tsupply: 蒸发器出口空气温度 (°C)
- pd: 排气压力 (bar)
- wij: 输入层到隐藏层权重矩阵 (hidden_nodes x 3)
- b1: 隐藏层偏置向量 (hidden_nodes x 1)
- wjm: 隐藏层到输出层权重矩阵 (1 x hidden_nodes)
- b2: 输出层偏置 (标量)
返回:
- COPr: 预测的制冷单元性能系数
基于Eq. (22): COPr = wjm • f(wij • [ta, tsupply, pd]^T - b1) - b2
"""
# 输入向量
inputs = np.array([[ta, tsupply, pd]]).T # (3 x 1)
# 隐藏层计算
hidden_input = np.dot(wij, inputs) - b1 # (hidden_nodes x 1)
hidden_output = sigmoid(hidden_input) # (hidden_nodes x 1)
# 输出层
COPr = np.dot(wjm, hidden_output) - b2 # 标量
return COPr.item() # 返回标量
# 示例使用,占位权重(用论文Appendix C中的实际值替换)
# 注意:论文指出神经网络连接矩阵wjm, wij和阈值b1, b2在Appendix C中。
# 由于文档中未提供Appendix C,我们使用随机占位符进行演示。
# 实际使用时,从论文加载训练好的权重。
hidden_nodes = 5 # 示例;实际数量应匹配训练模型
wij = np.random.randn(hidden_nodes, 3) # 输入权重 (hidden x 3)
b1 = np.random.randn(hidden_nodes, 1) # 隐藏偏置
wjm = np.random.randn(1, hidden_nodes) # 输出权重 (1 x hidden)
b2 = np.array([[0.0]]) # 输出偏置
# 使用样本工况测试
ta = 35.0 # 环境温度 (°C)
tsupply = 25.0 # 送风温度 (°C)
pd = 100.0 # 排气压力 (bar)
predicted_COPr = predict_COPr(ta, tsupply, pd, wij, b1, wjm, b2)
print(f"预测的COPr (制冷单元): {predicted_COPr:.4f}")
# 可选:批量预测多个工况
def batch_predict_COPr(inputs_array, wij, b1, wjm, b2):
"""
为多个工况预测COPr。
inputs_array: (N x 3) 数组,包含[ta, tsupply, pd]
"""
inputs = inputs_array.T # (3 x N)
hidden_input = np.dot(wij, inputs) - b1 # (hidden x N)
hidden_output = sigmoid(hidden_input)
COPr_values = np.dot(wjm, hidden_output) - b2 # (1 x N)
return COPr_values.flatten()
# 示例批量
conditions = np.array([
[30.0, 24.0, 90.0],
[35.0, 26.0, 100.0],
[40.0, 28.0, 110.0]
])
COPr_batch = batch_predict_COPr(conditions, wij, b1, wjm, b2)
print("批量COPr预测:", COPr_batch)该 BP 神经网络是灰箱模型的核心黑箱部分,负责将复杂非线性制冷过程简化为快速可调用的输入-输出映射,为 MPC 提供实时、准确的未来性能预测。