文章目录
前言
本文介绍了顺序查找算法的基本实现与优化方法。顺序查找是一种线性查找算法,通过逐一比较元素实现查找。文章首先给出了顺序查找的一般实现代码,然后介绍了哨兵机制优化方法,该方式通过减少越界判断提高效率。对于有序表的情况,可以通过提前终止查找进一步优化性能。此外,还讨论了根据元素被查概率调整存储位置的优化策略,虽然能提高查找成功效率,但会影响查找失败时的性能。最后指出顺序查找的时间复杂度始终为O(n)。本文通过算法思想、代码实现、效率分析和优化策略,全面介绍了顺序查找这一基础算法。
一.顺序查找的算法思想
- 顺序查找,又叫"线性查找",通常用于线性表。
- 算法思想:从头到脚挨个找(或者反过来也OK)
二.顺序查找的实现
1.一般实现
1.实现思路
- 从前往后依次寻找与查找目标关键字相同的元素
2.实现代码
c
typedef struct{ //查找表的数据结构(顺序表)
Element *elem; //动态数组基址
int TableLen; //表的长度
}SSTable;
//顺序查找
int Search_Seq(SSTable ST, ElemType key){
int i;
for(i=0; i<ST. TableLen && ST. elem[i]!=key; ++i);
//查找成功,则返回元素下标;查找失败,则返回-1
return i==ST. TableLen?-1:i;
}
2.哨兵实现顺序查找
1.实现思路
- 把0号位置给空出来,就是说我们实际的那些数据是从1这个位置开始存放的
- 当我们要查找某一个关键字的时候,会把这个关键字放到0号位置这个地方(哨兵)
- 然后接下来我们会让指针从最后一个位置开始往前扫描,如果当前指向了这个元素的值和我们的目标不一样,那么我们就会向前一直往前走
2.代码
c
typedef struct{//查找表的数据结构(顺序表)
ElementType *elem; //动态数组基址
int TableLen; //表的长度
}SSTable;
//顺序查找
int Search_Seq(SSTable ST, ElementType key){
ST.elem[0]=key; //"哨兵"
int i;
for(i=ST.TableLen; ST.elem[i]!=key;--i); //从后往前找
return i; //查找成功,则返回元素下标;查找失败,则返回0
}3.优点
- 在每一轮for循环的时候,我们只需要判断当前指向的元素和我们要找的那个关键字是否相等,而不用判断是否已经遍历完所有元素
- 优点:无需判断是否越界,效率更高
4.执行效率
- A S L = ∑ i = 1 n P i C i ASL=∑_{i=1}^{n}PᵢCᵢ ASL=∑i=1nPiCi
- 查找成功的情况: A S L 成功 = 1 + 2 + 3 + ⋯ + n n = n + 1 2 ASL_\text{成功}=\frac{1+2+3+\cdots+n}{n}=\frac{n+1}{2} ASL成功=n1+2+3+⋯+n=2n+1
- 查找失败的情况: A S L 失败 = n + 1 ASL_\text{失败}=n+1 ASL失败=n+1
三.顺序查找的优化(对有序表)
1.思路
-
只需要查找到我们大于21的值就不必再往后查找
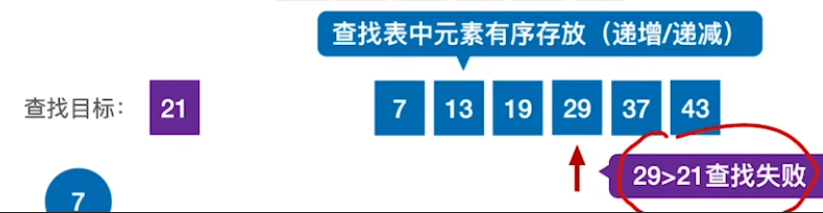
-
有序表的查找判定树
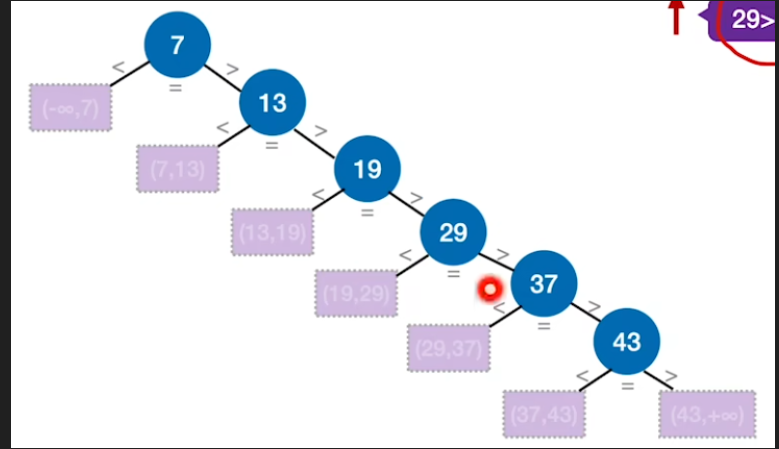
2.执行效率
1.执行失败
- 因为有n加一个这样的失败节点(查找判定树中的左孩子和最后一个节点的右孩子),共有n+1种查找失败的情况
- 假定说出现这n+1种情况的概率都是相等的,所以如果我们想要查找的那个关键字的值落在了第一个区间内,那么其实总共只需要对比一次关键字就可以了,而发生这种情况的概率是 1 n + 1 \frac{1}{n+1} n+11
- 以此类推,最终查找失败的平均查找长度为: A S L 失败 = 1 + 2 + 3 + ... + n + n n + 1 = n 2 + n n + 1 ASL_\text{失败}=\frac{1+2+3+\dotsc+n+n}{n+1}=\frac{n}{2}+\frac{n}{n+1} ASL失败=n+11+2+3+...+n+n=2n+n+1n
最后我们加了两个n,原因在于最下面的这两种失败情况(43的左右孩子),肯定都是需要把前面的n个元素都全部给对比一遍,所以这两种失败的情况都是要对比n次关键字
2.优势
- 很显然,对比普通的查找方法,它的执行失败的ASL更少
3.用查找判定树分析ASL
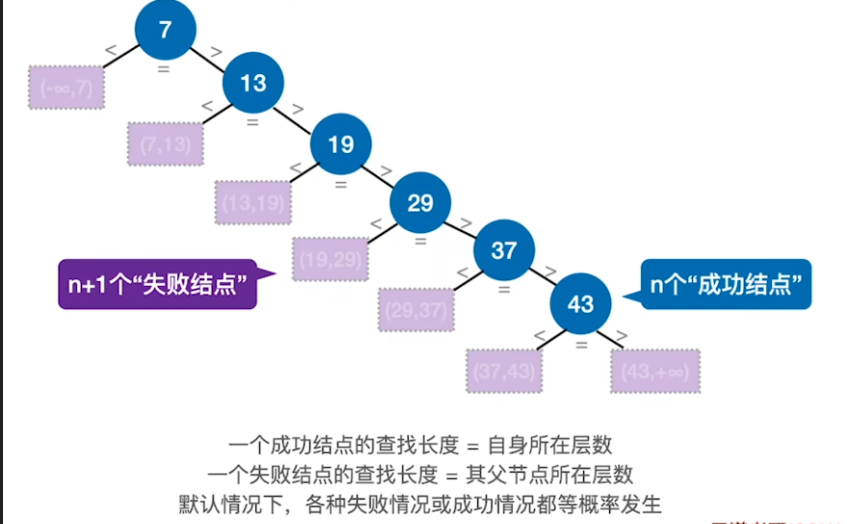
- 一个成功结点的查找长度 = 自身所在层数
- 一个失败结点的查找长度 =其父节点所在层数
- 默认情况下,各种失败情况或成功情况都等概率发生
四.顺序查找的优化(被查概率不相等)
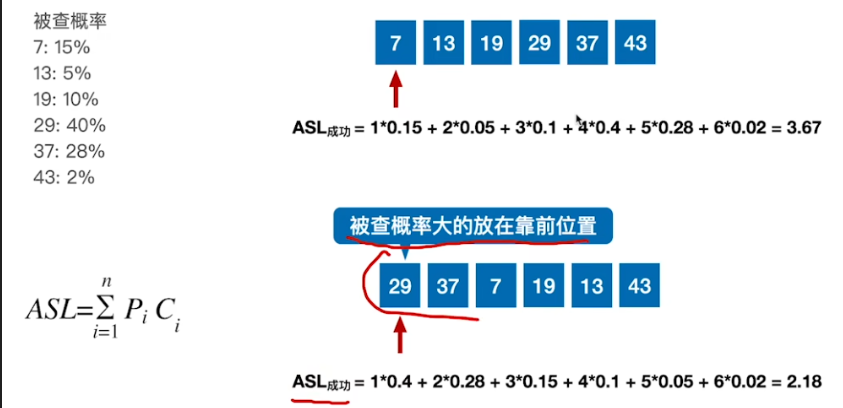
- 把被查找的概率更大的这些关键字放到更靠前的位置
- 这么做可以使得当我们在查找成功的情况下,平均查找长度能够更进一步的缩短
- 这样优化就会导致关键字的值又变成了乱序,这样做可以提高查找成功的平均查找长度,但是对于查找失败的情况又只能从头扫到尾
五.知识回顾与重要考点
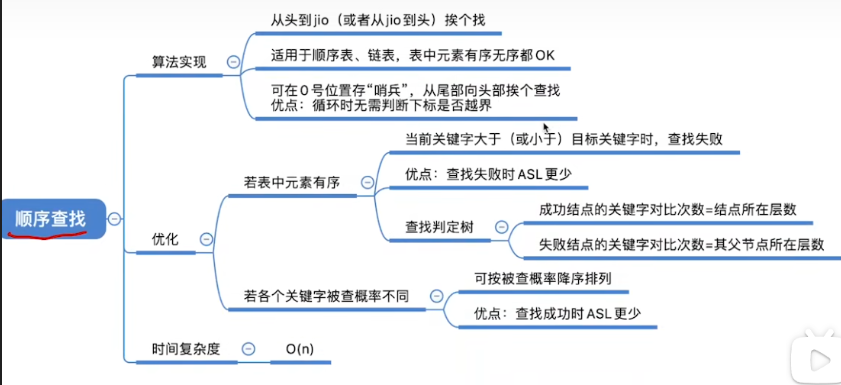
- 只要你采用的是顺序查找的这种基本策略,算法时间复杂度肯定都是O(n)这样的一个数量级
结语
最近被学校的琐事缠住了,只能暂时停更😖
如果想查看更多章节,请点击:一、数据结构专栏导航页