逻辑回归理论
逻辑回归是监督学习最主要的类型之一。它的标签是离散的
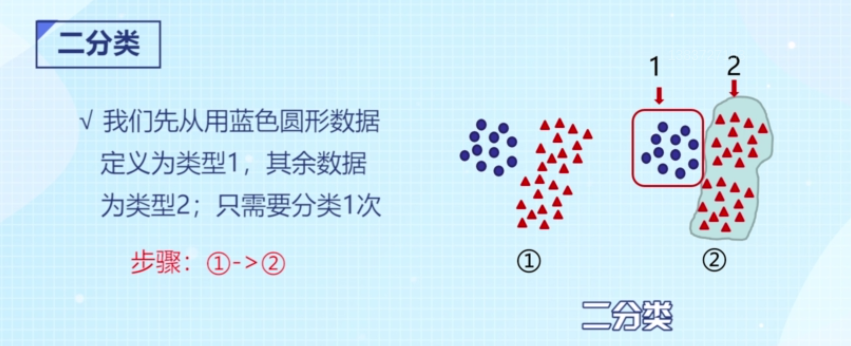
分类还分为二分类和多分类。输入的特征变量可以是连续或离散的,输出变量(标签)是离散的,多分类问题可以转换为二分类问题,二分类只需要一次,把一个类别分出来,剩下!的就是另外一类
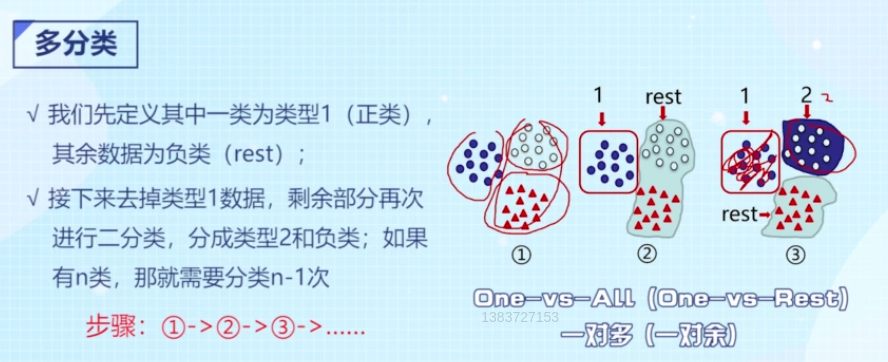
多分类问题可以转化为多次二分类问题,第一次分A和非A,第二次在非A里面分B和非B
关于二分类,我们的模型理想状态下定义为输入x,输出f(x)>0,则认为类别1,否则类别2,它的损失函数可以通过统计预测值和真实值不等的次数来评估,下面的δ(fxn)≠y^n\delta(fx^n)\neq \hat{y}^nδ(fxn)=y^n在满足条件时为1,不满足为0

但这里这个L(f)我们没法用连续的微分方式去求解最优值,也有其他方式如感知机,svm向量机的方式去求解找到最优的function
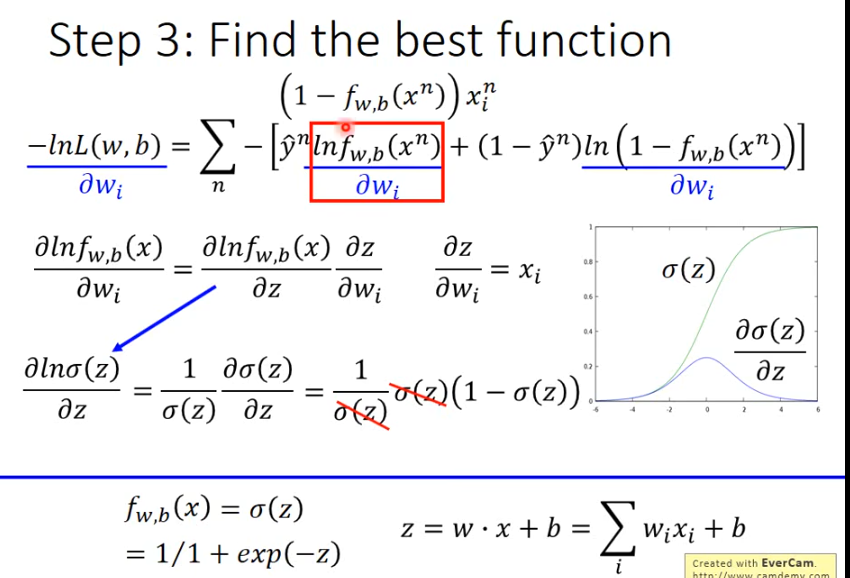
下面按李宏毅老师的方法,逐步去定义L(f)

假设知道了从B1中取出蓝色求的概率和从B2中取出绿色球的概率,那么取出蓝色球,它是来自于B1的概率即从B1取的概率P(B1) 乘以B1中取出蓝色球的概率P(Blue|B1)再除以总的取出蓝色球的概率P(Blue|B1)P(B1) + P(Blue|B2)P(B2),P(B1)+P(B2)应等于1,而在分类中,我们正是关注当有一个变量x时,它属于哪一个类别的概率比较大,那么它就最可能划分为哪一类。
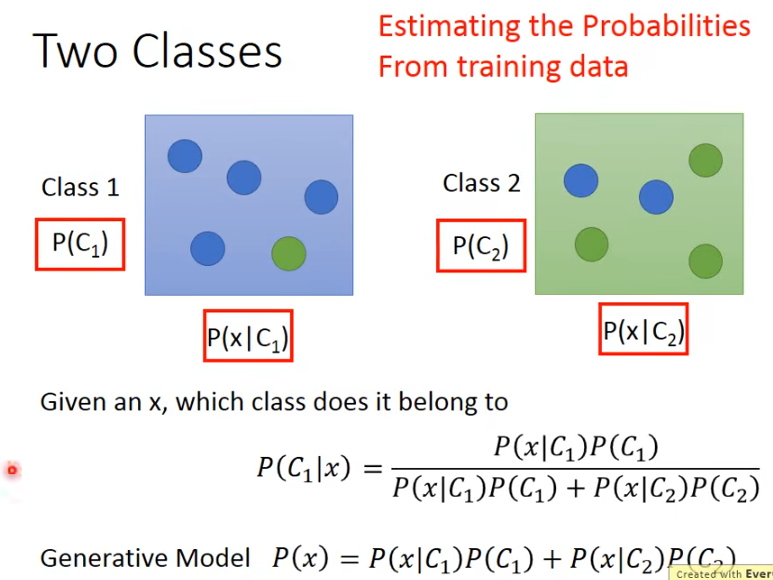
在分类里面,取出x的概率p(x)=p(x|c1)p(c1) + p(x|c2)P(c2)叫作一个生成式模型
假设我们有一堆样本,满足高斯分布,从样本中采样79个点的,这79个点是独立采样的,他们总的机率就是各自的机率相乘(这里描述为机率并不准确,应该是概率密度),找到使采样样本出现机率最大的参数,μ\muμ和σ\sigmaσ(下面是∑\sum∑表示)就是我们的目标,而这样的方法叫最大似然法。
我们是假设类C1满足一种高斯分布,类C2满足另外一种不同参数的高斯分布,只要确定了其参数,代入任意一个点都能确认它的机率,那么它满足哪个高斯分布的机率高,更有可能属于哪个类别。
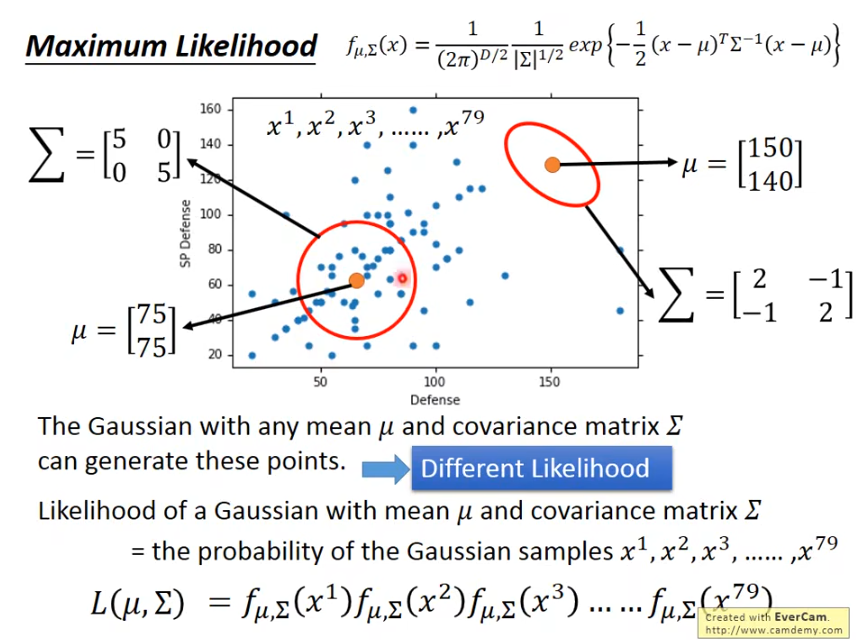

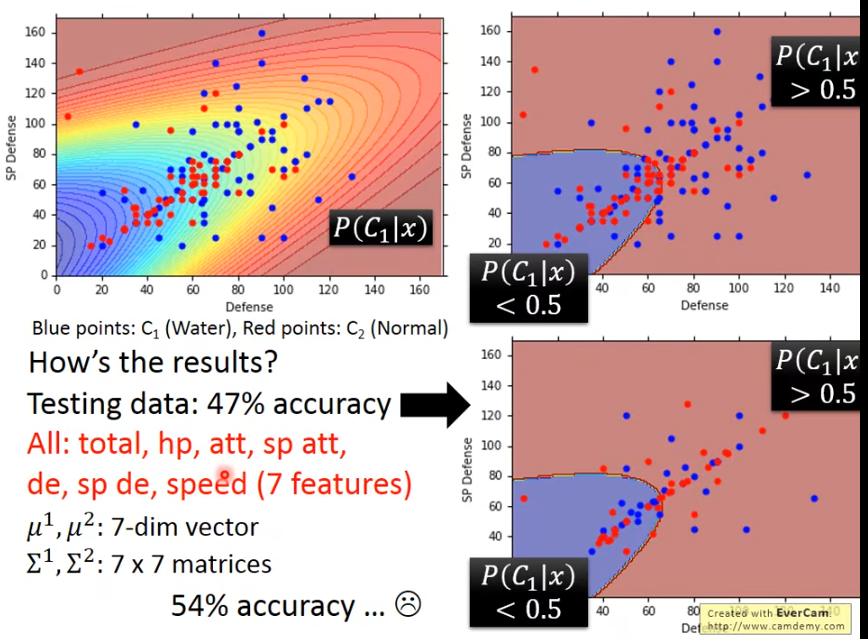
假设水属性的pokemon所属的分布参数和常规的不同,μ\muμ和σ\sigmaσ都不同的场景下,并不一定能得到好的结果,假设σ\sigmaσ一致


也就是找到一个概率分布,能最大化似然值(数据从中产生的概率)
为什么选择高斯分布?
选任何一个概率模型都可以,选高斯只是一个例子


做逻辑回归
前面的理论已经说明了为什么σ(z)\sigma (z)σ(z)是这样定义,以及为什么z=w*x+b
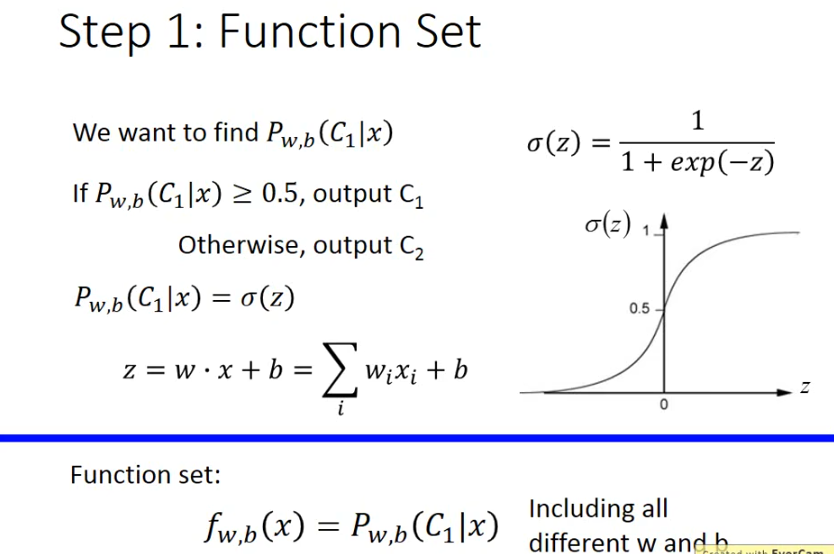
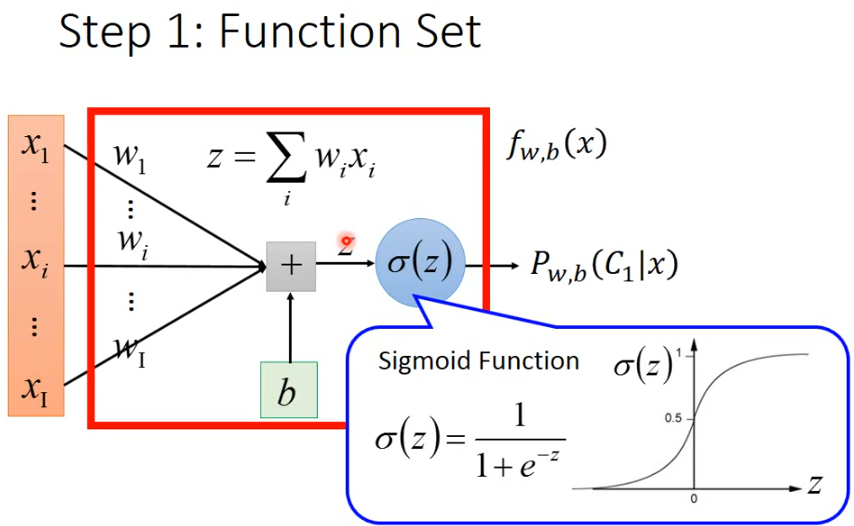
可以看到,逻辑回归通过σ\sigmaσ将f限定在了0-1之间
如何评估模型好坏

给定一组w,b集合,产生training data的概率为如上公式,找到这样一组w,b使得L最大
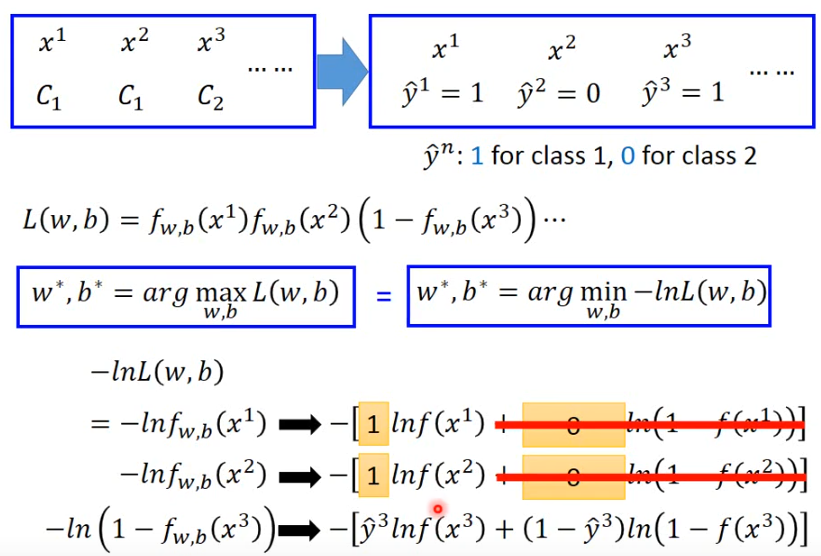
下面的式子中,令x在类1时y=1,x在类2时为0,就可以写成一个交叉熵的式子

交叉熵反映的时这两个分布p,q有多相似

用梯度下降求最优解,对L(f)做偏微分