把ITPUB newkid先生编写的Oracle语法数独求解SQL改写成DuckDB

原答案是用绑定变量的，为了改写成表的列，增加了ANY_VALUE函数。然后为了存下整个表格81格点的位置，用了hugeint。

sql 复制代码

WITH recursive b as(
--select '53..7....6..195....98....6.8...6...34..8.3..17...2...6.6....28....419..5....8..79' b),
--select '8..........36......7..9.2...5...7.......457.....1...3...1....68..85...1..9....4..' b),
select '9......4..5..2........1......69..1........5.24..7......1....3.....6...9....4.....' b),
d(z, lp) AS (
    VALUES('1', 1)
    UNION ALL SELECT
    CAST(lp+1 AS TEXT), lp+1 FROM d WHERE lp<81
  ),
grid AS (
SELECT lp                                                   AS pos
      ,(lp-1)//9                                      AS r  
      ,(lp-1)%9                                          AS c  
      ,(lp-1)//9//3*3 + (lp-1)%9//3 AS g  
  FROM D
)
,all_pos AS (  
SELECT pos,n
      ,1::hugeint<< (grid.r*9+n-1) AS r
      ,1::hugeint<< (grid.c*9+n-1) AS c
      ,1::hugeint<< (grid.g*9+n-1) AS g
  FROM grid,(SELECT lp n FROM D where lp<=9)
)
,t(s,rs,cs,gs,next_pos) AS (
SELECT CAST(ANY_VALUE(b) AS text)
       ,SUM(all_pos.r) rs   ---------- 哪些位置已经被占用
       ,SUM(all_pos.c) cs
       ,SUM(all_pos.g) gs
       ,INSTR(ANY_VALUE(b),'.')  
   FROM all_pos,b
  WHERE SUBSTR(b,all_pos.pos,1)=cast(all_pos.n as text)
  UNION ALL
  SELECT SUBSTR(t.s,1,t.next_pos-1)||a.n||SUBSTR(t.s,t.next_pos+1)
        ,t.rs+a.r
        ,t.cs+a.c
        ,t.gs+a.g
        ,case INSTR(SUBSTR(t.s,t.next_pos+1),'.') when 0 then 0 else INSTR(SUBSTR(t.s,t.next_pos+1),'.')+t.next_pos end
    FROM t
        ,all_pos a
   WHERE t.next_pos = a.pos
         AND (t.rs&a.r)=0
         AND (t.cs&a.c)=0
         AND (t.gs&a.g)=0
)
--select count() from t;
--select next_pos,count() from t group by next_pos;
SELECT t.s FROM t WHERE next_pos=0;

目前最快，用预计算消除了迭代中的计算行列坐标，奇怪的是我把它求位置的方法改写到数组版本，反而更慢了。可能取数组下标也是费时的操作。

复制代码

--数组版本
D .read test-cnt2.txt
 (00:00:05.53 elapsed) 
--Oracle改写版本
D .read nkdsudoku.txt
 (00:00:02.88 elapsed) 
--改写后数组版本
.read test-cnt2a2.txt
 (00:00:08.85 elapsed)

后记，把原题中

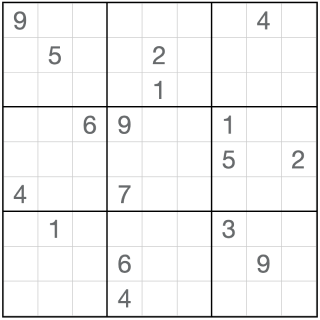
的中间三行放在最上面，Oracle用时只要原来的1/3

复制代码

select '..69..1........5.24..7......1....3.....6...9....4.....9......4..5..2........1....' b),

Run Time (s): real 1.215 user 1.020000 sys 0.112000