如何找到一个矩阵的特征值和特征向量

如何找到一个矩阵的特征值和特征向量

flyfish

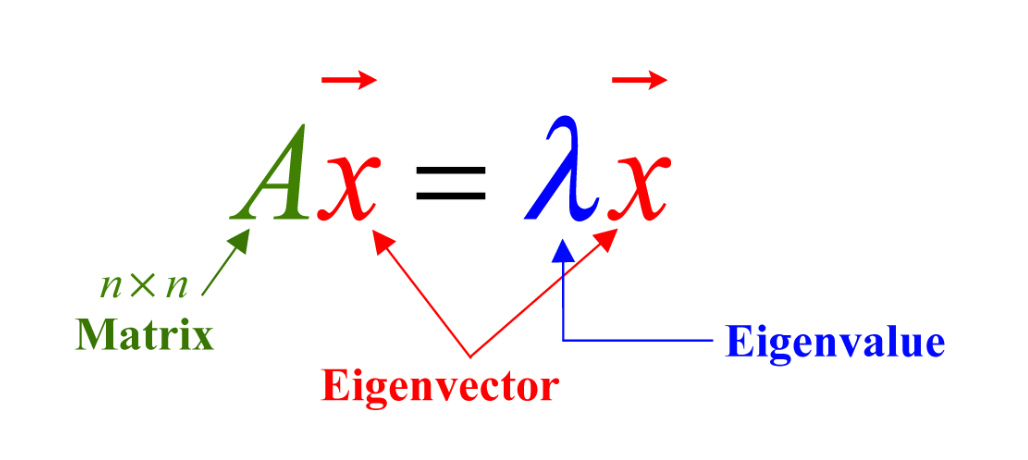
仅方阵存在特征值和特征向量；

特征向量是非零向量，特征值可以是任意实数（包括0）；

以2×2矩阵为例的求解步骤

步骤1：求矩阵的特征值

通过公式 det⁡(A−λI)=0\det(A - \lambda I) = 0det(A−λI)=0 计算，其中：

• AAA 是待分析的2×2矩阵；
• λ\lambdaλ 是特征值（未知数）；
• III 是单位矩阵（主对角线为1，其余为0的矩阵）；
• det⁡(⋅)\det(\cdot)det(⋅) 表示计算矩阵的行列式。

利用"特征值满足齐次线性方程组 (A−λI)v=0(A - \lambda I)v = 0(A−λI)v=0 有非零解"的性质，而齐次方程组有非零解的充要条件是系数矩阵的行列式为0 ，因此推导出 det⁡(A−λI)=0\det(A - \lambda I) = 0det(A−λI)=0。

步骤2：求对应特征值的特征向量

将步骤1中求出的特征值 λ\lambdaλ 代入方程 (A−λI)v=0(A - \lambda I)v = 0(A−λI)v=0，求解非零向量 vvv（即特征向量）。

第一个例子

矩阵 A=[−6345]A = \begin{bmatrix} -6 & 3 \\ 4 & 5 \end{bmatrix}A=[−6435]

步骤1：明确公式

求矩阵特征值的公式是：∣A−λI∣=0|A - \lambda I| = 0∣A−λI∣=0

其中：

• AAA 是待求特征值的矩阵；
• λ\lambdaλ 是特征值（我们要求的未知数）；
• III 是单位矩阵（主对角线为1，其余为0的矩阵）；
• ∣⋅∣|\cdot|∣⋅∣ 表示计算矩阵的行列式。

步骤2：构造 A−λIA - \lambda IA−λI

矩阵 A=[−6345]A = \begin{bmatrix} -6 & 3 \\ 4 & 5 \end{bmatrix}A=[−6435]，单位矩阵 I=[1001]I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}I=[1001]，则：
A−λI=[−6345]−λ[1001]=[−6−λ345−λ] A - \lambda I = \begin{bmatrix} -6 & 3 \\ 4 & 5 \end{bmatrix} - \lambda \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} -6-\lambda & 3 \\ 4 & 5-\lambda \end{bmatrix} A−λI=[−6435]−λ[1001]=[−6−λ435−λ]

步骤3：计算行列式 ∣A−λI∣|A - \lambda I|∣A−λI∣

对于2×2矩阵 [abcd]\begin{bmatrix} a & b \\ c & d \end{bmatrix}[acbd]，行列式公式为 ad−bcad - bcad−bc。

这里 a=−6−λa = -6-\lambdaa=−6−λ，b=3b = 3b=3，c=4c = 4c=4，d=5−λd = 5-\lambdad=5−λ，因此：
∣A−λI∣=(−6−λ)(5−λ)−3×4 |A - \lambda I| = (-6-\lambda)(5-\lambda) - 3 \times 4 ∣A−λI∣=(−6−λ)(5−λ)−3×4

步骤4：展开并化简行列式，得到二次方程

先展开 (−6−λ)(5−λ)(-6-\lambda)(5-\lambda)(−6−λ)(5−λ)：
(−6−λ)(5−λ)=−6×5+(−6)×(−λ)+(−λ)×5+(−λ)×(−λ)=−30+6λ−5λ+λ2=λ2+λ−30 \begin{align*} (-6-\lambda)(5-\lambda) &= -6 \times 5 + (-6) \times (-\lambda) + (-\lambda) \times 5 + (-\lambda) \times (-\lambda) \\ &= -30 + 6\lambda - 5\lambda + \lambda^2 \\ &= \lambda^2 + \lambda - 30 \end{align*} (−6−λ)(5−λ)=−6×5+(−6)×(−λ)+(−λ)×5+(−λ)×(−λ)=−30+6λ−5λ+λ2=λ2+λ−30

再减去 3×4=123 \times 4 = 123×4=12，得到：
λ2+λ−30−12=λ2+λ−42 \lambda^2 + \lambda - 30 - 12 = \lambda^2 + \lambda - 42 λ2+λ−30−12=λ2+λ−42

因此，特征方程为：
λ2+λ−42=0 \lambda^2 + \lambda - 42 = 0 λ2+λ−42=0

步骤5：解二次方程，得到特征值

对 λ2+λ−42=0\lambda^2 + \lambda - 42 = 0λ2+λ−42=0 进行因式分解 （或用求根公式）。

寻找两个数，使其乘积为 -42 ，且和为 1 ，可得这两个数是 777 和 −6-6−6，因此：
(λ+7)(λ−6)=0 (\lambda + 7)(\lambda - 6) = 0 (λ+7)(λ−6)=0

解得：
λ=−7或λ=6 \lambda = -7 \quad \text{或} \quad \lambda = 6 λ=−7或λ=6

矩阵 AAA 的两个特征值为 −7{-7}−7 和 6{6}6。

已知矩阵的特征值 λ=6\lambda = 6λ=6，求其对应的特征向量 （即满足 Av=λvAv = \lambda vAv=λv 的非零向量 vvv）。

步骤1：明确特征向量的定义式

特征向量 vvv 需满足 Av=λv{Av = \lambda v}Av=λv（v≠0v \neq \mathbf{0}v=0）。

已知矩阵 A=[−6345]A = \begin{bmatrix} -6 & 3 \\ 4 & 5 \end{bmatrix}A=[−6435]，特征值 λ=6\lambda = 6λ=6，设特征向量 v=[xy]v = \begin{bmatrix} x \\ y \end{bmatrix}v=[xy]（非零列向量）。

步骤2：代入定义式，展开矩阵乘法

将 AAA、λ\lambdaλ、vvv 代入 Av=λvAv = \lambda vAv=λv：

−6345\]\[xy\]=6\[xy\] \\begin{bmatrix} -6 \& 3 \\\\ 4 \& 5 \\end{bmatrix} \\begin{bmatrix} x \\\\ y \\end{bmatrix} = 6 \\begin{bmatrix} x \\\\ y \\end{bmatrix} \[−6435\]\[xy\]=6\[xy

左边矩阵乘向量后得到：

−6x+3y4x+5y\]=\[6x6y\] \\begin{bmatrix} -6x + 3y \\\\ 4x + 5y \\end{bmatrix} = \\begin{bmatrix} 6x \\\\ 6y \\end{bmatrix} \[−6x+3y4x+5y\]=\[6x6y

步骤3：转化为线性方程组并化简

根据向量相等的定义，对应分量相等，得到两个方程：
{−6x+3y=6x4x+5y=6y \begin{cases} -6x + 3y = 6x \\ 4x + 5y = 6y \end{cases} {−6x+3y=6x4x+5y=6y

将所有项移到左边，化简得：
{−12x+3y=04x−y=0 \begin{cases} -12x + 3y = 0 \\ 4x - y = 0 \end{cases} {−12x+3y=04x−y=0

这两个方程是等价的 （第二个方程两边乘3即可得到第一个方程），只需解其中一个，比如 4x−y=04x - y = 04x−y=0，可得 y=4x{y = 4x}y=4x。

步骤4：确定特征向量的形式

因为 y=4xy = 4xy=4x，xxx 可取任意非零常数 （特征向量不能是零向量）。

令 x=1x = 1x=1，则 y=4y = 4y=4，得到一个基础特征向量：
v=[14] v = \begin{bmatrix} 1 \\ 4 \end{bmatrix} v=[14]

所有与 [14]\begin{bmatrix} 1 \\ 4 \end{bmatrix}[14] 成非零倍数 的向量（如 k[14],k≠0k\begin{bmatrix} 1 \\ 4 \end{bmatrix}, k \neq 0k[14],k=0），都是 λ=6\lambda = 6λ=6 对应的特征向量。

步骤5：验证解的正确性

将 v=[14]v = \begin{bmatrix} 1 \\ 4 \end{bmatrix}v=[14] 代入 AvAvAv 和 λv\lambda vλv，验证是否相等：

• 计算 AvAvAv：

  −6345\]\[14\]=\[−6×1+3×44×1+5×4\]=\[624\] \\begin{bmatrix} -6 \& 3 \\\\ 4 \& 5 \\end{bmatrix} \\begin{bmatrix} 1 \\\\ 4 \\end{bmatrix} = \\begin{bmatrix} -6 \\times 1 + 3 \\times 4 \\\\ 4 \\times 1 + 5 \\times 4 \\end{bmatrix} = \\begin{bmatrix} 6 \\\\ 24 \\end{bmatrix} \[−6435\]\[14\]=\[−6×1+3×44×1+5×4\]=\[624

• 计算 λv\lambda vλv：
  6[14]=[624] 6 \begin{bmatrix} 1 \\ 4 \end{bmatrix} = \begin{bmatrix} 6 \\ 24 \end{bmatrix} 6[14]=[624]
  两者相等，说明 [14]\begin{bmatrix} 1 \\ 4 \end{bmatrix}[14] 是 λ=6\lambda = 6λ=6 对应的特征向量。

λ=−7\lambda = -7λ=−7 也是一个有效的特征值，同样可以按照完全相同的步骤求它对应的特征向量：

1. 代入 Av=λvAv = \lambda vAv=λv，即 [−6345][xy]=−7[xy]\begin{bmatrix} -6 & 3 \\ 4 & 5 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = -7 \begin{bmatrix} x \\ y \end{bmatrix}[−6435][xy]=−7[xy]；
2. 展开得到方程组 {−6x+3y=−7x4x+5y=−7y\begin{cases} -6x + 3y = -7x \\ 4x + 5y = -7y \end{cases}{−6x+3y=−7x4x+5y=−7y，化简为 {x+3y=04x+12y=0\begin{cases} x + 3y = 0 \\ 4x + 12y = 0 \end{cases}{x+3y=04x+12y=0；
3. 解得 x=−3yx = -3yx=−3y，令 y=1y = 1y=1，则特征向量为 [−31]\begin{bmatrix} -3 \\ 1 \end{bmatrix}[−31]（或其非零倍数，如 k[−31],k≠0k\begin{bmatrix} -3 \\ 1 \end{bmatrix}, k \neq 0k[−31],k=0）。

第二个例子

要解决矩阵 A=[1254]A = \begin{bmatrix} 1 & 2 \\ 5 & 4 \end{bmatrix}A=[1524] 的特征值和特征向量问题，先求特征值，再对每个特征值求对应特征向量

一、求特征值（解 det⁡(A−λI)=0\det(A - \lambda I) = 0det(A−λI)=0）

特征值的定义是满足 det⁡(A−λI)=0\det(A - \lambda I) = 0det(A−λI)=0 的常数 λ\lambdaλ，其中：

• I=[1001]I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}I=[1001] 是单位矩阵；
• det⁡(⋅)\det(\cdot)det(⋅) 表示矩阵的行列式。

步骤1：构造 A−λIA - \lambda IA−λI

A−λI=[1−λ254−λ] A - \lambda I = \begin{bmatrix} 1-\lambda & 2 \\ 5 & 4-\lambda \end{bmatrix} A−λI=[1−λ524−λ]

步骤2：计算行列式并化简

对于2×2矩阵 [mnpq]\begin{bmatrix} m & n \\ p & q \end{bmatrix}[mpnq]，行列式为 mq−npmq - npmq−np，因此：
det⁡(A−λI)=(1−λ)(4−λ)−2×5=4−λ−4λ+λ2−10=λ2−5λ−6=(λ−6)(λ+1) \begin{align*} \det(A - \lambda I) &= (1-\lambda)(4-\lambda) - 2 \times 5 \\ &= 4 - \lambda - 4\lambda + \lambda^2 - 10 \\ &= \lambda^2 - 5\lambda - 6 \\ &= (\lambda - 6)(\lambda + 1) \end{align*} det(A−λI)=(1−λ)(4−λ)−2×5=4−λ−4λ+λ2−10=λ2−5λ−6=(λ−6)(λ+1)

步骤3：解方程 det⁡(A−λI)=0\det(A - \lambda I) = 0det(A−λI)=0

(λ−6)(λ+1)=0  ⟹  λ=6 或 λ=−1 (\lambda - 6)(\lambda + 1) = 0 \implies \lambda = 6 \text{ 或 } \lambda = -1 (λ−6)(λ+1)=0⟹λ=6 或 λ=−1

二、求特征值 λ=6\lambda = 6λ=6 对应的特征向量（解 (A−6I)v=0(A - 6I)v = 0(A−6I)v=0）

特征向量 v=[ab]v = \begin{bmatrix} a \\ b \end{bmatrix}v=[ab] 需满足 (A−λI)v=0(A - \lambda I)v = \mathbf{0}(A−λI)v=0（0\mathbf{0}0 是零向量）。

步骤1：构造 A−6IA - 6IA−6I

A−6I=[1−6254−6]=[−525−2] A - 6I = \begin{bmatrix} 1-6 & 2 \\ 5 & 4-6 \end{bmatrix} = \begin{bmatrix} -5 & 2 \\ 5 & -2 \end{bmatrix} A−6I=[1−6524−6]=[−552−2]

步骤2：解方程组 (A−6I)v=0(A - 6I)v = \mathbf{0}(A−6I)v=0

−525−2\]\[ab\]=\[00\] \\begin{bmatrix} -5 \& 2 \\\\ 5 \& -2 \\end{bmatrix} \\begin{bmatrix} a \\\\ b \\end{bmatrix} = \\begin{bmatrix} 0 \\\\ 0 \\end{bmatrix} \[−552−2\]\[ab\]=\[00

即：
−5a+2b=0  ⟹  5a=2b -5a + 2b = 0 \implies 5a = 2b −5a+2b=0⟹5a=2b

步骤3：确定特征向量

令 a=2a = 2a=2，则 b=5b = 5b=5，因此特征向量为：
v=[25](所有非零倍数均为特征向量) v = \begin{bmatrix} 2 \\ 5 \end{bmatrix} \quad (\text{所有非零倍数均为特征向量}) v=[25](所有非零倍数均为特征向量)

三、求特征值 λ=−1\lambda = -1λ=−1 对应的特征向量（解 (A+I)v=0(A + I)v = 0(A+I)v=0）

步骤1：构造 A+IA + IA+I

A+I=[1+1254+1]=[2255] A + I = \begin{bmatrix} 1+1 & 2 \\ 5 & 4+1 \end{bmatrix} = \begin{bmatrix} 2 & 2 \\ 5 & 5 \end{bmatrix} A+I=[1+1524+1]=[2525]

步骤2：解方程组 (A+I)v=0(A + I)v = \mathbf{0}(A+I)v=0

2255\]\[ab\]=\[00\] \\begin{bmatrix} 2 \& 2 \\\\ 5 \& 5 \\end{bmatrix} \\begin{bmatrix} a \\\\ b \\end{bmatrix} = \\begin{bmatrix} 0 \\\\ 0 \\end{bmatrix} \[2525\]\[ab\]=\[00

即：
2a+2b=0  ⟹  a=−b 2a + 2b = 0 \implies a = -b 2a+2b=0⟹a=−b

步骤3：确定特征向量

令 a=1a = 1a=1，则 b=−1b = -1b=−1，因此特征向量为：
v=[1−1](所有非零倍数均为特征向量) v = \begin{bmatrix} 1 \\ -1 \end{bmatrix} \quad (\text{所有非零倍数均为特征向量}) v=[1−1](所有非零倍数均为特征向量)

矩阵 AAA 的特征值为 λ=6{\lambda = 6}λ=6 和 λ=−1{\lambda = -1}λ=−1；

对应特征值 666 的特征向量为 [25]{\begin{bmatrix} 2 \\ 5 \end{bmatrix}}[25]（及非零倍数）；

对应特征值 −1-1−1 的特征向量为 [1−1]{\begin{bmatrix} 1 \\ -1 \end{bmatrix}}[1−1]（及非零倍数）。