1. 二叉树
1.1 每个节点最多有两个分支,分别为左子节点和右子节点。
1.2 不要求每个节点都有两个子节点,有的节点可以只有左子节点或右子节点。
1.3 二叉树每个节点的左子树和右子树均为二叉树。
2. 二叉搜索树
2.1 又名二叉查找树、有序二叉树
2.2 在树的任意一个节点,其左子树的每个节点的值都要小于该节点的值,其右子树的每个节点的值都要大于该节点的值。
2.3 没有键值相等的节点
2.4 通常情况下搜索的时间复杂度为O(logn),除非退化为所有节点只有左子树或右子树的情况(链表)。
3. 红黑树(自平衡的二叉搜索树)
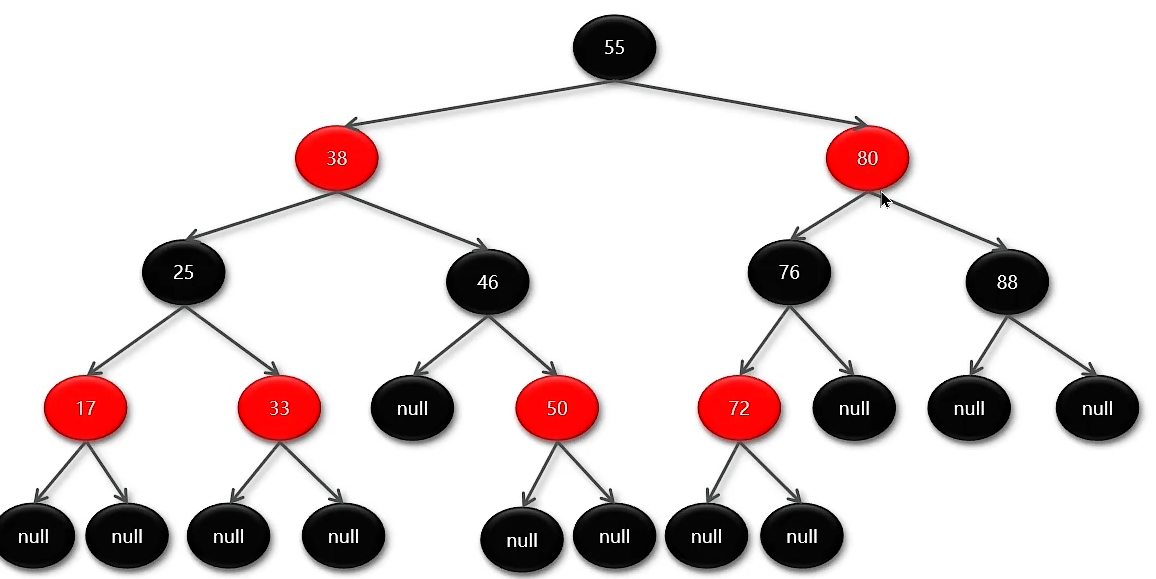
3.1 红黑树的规则:
- 节点要么是红色,要么是黑色
- 根节点为黑色
- 叶子结点都是黑色的空节点
- 红黑树中红色节点的子节点都是黑色
- 从任意节点到叶子结点的所有路径均包含相同数目的黑色节点
在添加或删除节点时,如果二叉树不再符合以上规则,该二叉树会发生旋转,使其符合上述规则,以保证树的平衡。
3.2 时间复杂度分析
3.2.1 查找 同二叉搜索树,为 O(log n)
3.2.2 添加和删除
先要从根节点开始查找元素添加的位置或需要删除的元素,时间复杂度为O(log n),完成后涉及到复杂度为O(1)的树旋转操作,最终的复杂度为O(log n)。
4. 散列表
在HashMap中最重要的数据结构即为散列表,在散列表中又使用到了红黑树和链表。
根据键 key 直接访问在内存存储位置的数据 value,通过数组演化而来,利用了数组支持下标进行随机访问数据的特性。
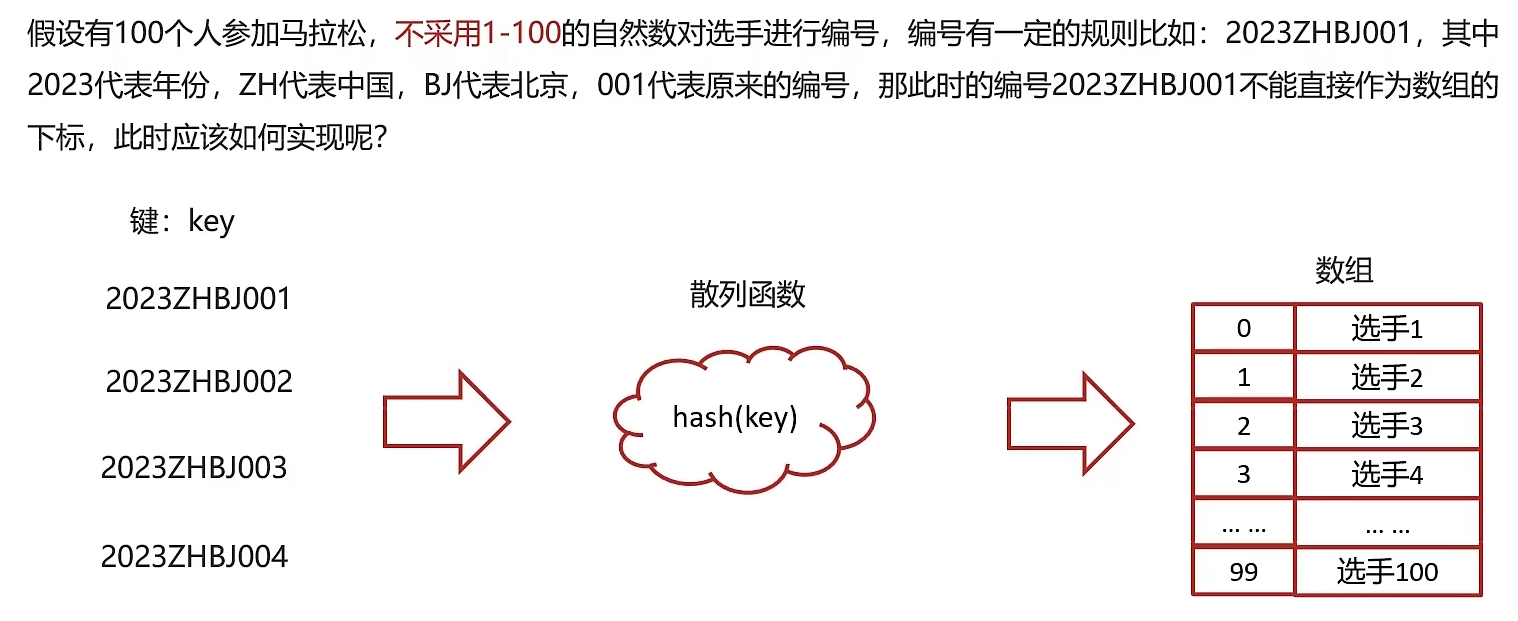
4.1 散列函数的基本要求:
- 结果必须为非负整数,可以作为数组下标
- 相同数据的哈希值必定相同
- 不同数据的哈希值必定不能相同
4.2 散列冲突
不同数据通过散列函数得到的散列值都不同在实际情况中几乎不可能,此时就出现了冲突的情况。也成为哈希冲突、哈希碰撞。
可使用拉链法解决上述的冲突问题,即在同一个下标值的地方存储一个链表,存储多个下表值相同的数据。

4.2.1 插入操作过程中,通过散列计算得出响应的槽位,将数据直接插入即可,时间复杂度为O(1)
4.2.2 查找、删除数据时,先得到响应的槽位,再遍历链表查找或者删除
平均情况下,基于链表解决冲突时,查询的时间复杂度为O(1)。
当散列表退化为链表,查询的时间复杂度即为O(n)。
将链表法中的链表改造为其他高效的动态数据结构,比如红黑树,查询的时间复杂度即为O(log n),此时可以有效的防止DDos攻击。
DDos攻击:分布式拒绝服务攻击,指处于不同位置的多个攻击者同时向一个或数个目标发起攻击,或者一个攻击者控制了位于不同位置的多台机器并利用这些机器对受害者同时实施攻击。由于攻击的出发点分布在不同的地方,这类攻击称为分布式拒绝服务攻击,其中的攻击者可以有多个。