此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本篇为第二课的第二周内容,2.8的内容,同时也是本周理论部分的最后一篇。
本周为第二课的第二周内容,和题目一样,本周的重点是优化算法,即如何更好,更高效地更新参数帮助拟合的算法,还是离不开那句话:优化的本质是数学 。
因此,在理解上,本周的难道要相对较高一些,公式的出现也会更加频繁。
当然,我仍会补充一些更基础的内容来让理解的过程更丝滑一些。
本篇的内容关于Adam优化算法,是在之前的Momentum和RMSprop基础上的集成算法。
1. Adam 优化算法
前面我们已经学过Momentum和RMSprop算法。
先回忆两个算法的核心思想:
| 算法 | 解决问题 | 技术手段 |
|---|---|---|
| Momentum | 梯度方向不稳定、震荡 | 平滑梯度 |
| RMSprop | 梯度幅度差异大 | 平滑梯度平方、调节步长 |
在上一篇最后,我们提到,二者在使用上并不冲突,可以结合使用。
而结合后的方法同时应用平滑梯度和平滑梯度平方,实现平稳方向和自适应步长。
这就是Adam优化算法。
说实话,从原理上讲,Adam基本就是把Momentum和RMSprop两种算法加起来 。
所以,只要能理解这两种算法,那Adam的理解基本不是问题,我们直接展开Adam算法的公式逻辑。
1.1 Adam 的基本思想
Adam 会维护两个量:
| 名称 | 含义 | 对应哪部分算法? |
|---|---|---|
| 一阶矩 vₜ | 平滑后的梯度(方向) | Momentum |
| 二阶矩 Sₜ | 平滑后的梯度平方(幅度) | RMSProp |
也就是说:
- vₜ = 用来稳方向
- Sₜ = 用来调步长
Adam = vₜ + Sₜ 的协作更新。
1.2 一二阶矩
(1)一阶矩:平滑梯度 vₜ
来自Momentum,我们用 vₜ 表示平滑梯度:
\[v_t = \beta_1 v_{t-1} + (1-\beta_1) g_t \]
这行的作用:平滑方向,避免梯度抖来抖去。
(2)二阶矩:平滑梯度平方 Sₜ
来自RMSprop,用 Sₜ 表示平滑梯度平方:
\[S_t = \beta_2 S_{t-1} + (1-\beta_2) g_t^2 \]
这行的作用:感知"梯度大小的平均幅度",用于自适应调步长。
1.3 一二阶矩为什么能起到相应作用?
再补充一点,你可能会有这样一个问题:
为什么用一阶矩来平滑方向,用二阶矩调节步长?这么设置的合理性在哪?他们能换个位置吗?
我们总地说一下梯度和梯度平方最大的区别:
- 梯度带正负号,包含方向信息
- 梯度平方一定为正,体现的是"幅度"
现在再展开看一下:
| 角色 | 是否保留方向(正负) | 代表的意义 | 最适合的任务 | 为什么不能反过来? |
|---|---|---|---|---|
| 一阶矩 vₜ | 保留正负号 | 过去梯度的加权平均(趋势/方向) | 按趋势稳定方向 | vₜ 会为正或负,不代表"大小趋势",无法判断步长是否应该缩放 |
| 二阶矩 Sₜ | 永远 ≥ 0(没方向) | 梯度平方的平均(尺度/大小) | 按尺度自适应调步长 | Sₜ 没有方向信息,无法告诉你"往左还是往右" |
总之,vₜ 和 Sₜ 的功能无法互换 ------ 一个负责"走哪边",一个负责"走多快"。
因此,我们不可能让速度决定方向,也不能让方向负责踩油门。
1.4 一二阶矩的偏差修正
因为 v₀ = 0、S₀ = 0,一开始偏小,所以 Adam 做偏差校正:
一阶矩修正:
\[\hat{v}_t = \frac{v_t}{1-\beta_1^t} \]
二阶矩修正:
\[\hat{S}_t = \frac{S_t}{1-\beta_2^t} \]
同样是之前就讲过的内容,我们用偏差修正来弥补EMA在初期偏小的情况,修正带来的影响也会在后期分母无限接近1的情况下自动消失。
1.5 Adam参数更新公式
到了这一步,我们先看看之前两种算法的更新公式:
首先是Momentum:
\[\theta_{t+1} = \theta_t - \alpha \cdot v_t,其中 v_t = \beta v_{t-1} + (1-\beta) g_t \]
这里,我们主要使用一阶矩 来形成"惯性",抵消样本参数的个性化特征信息同时加强共性特征信息来缓解"震荡"。如果你有些忘了为什么会有这种效果,再看看之前的详细解释:Momentum
然后,我们又引入RMSprop:
\[\theta_{t+1} = \theta_t - \alpha \cdot \dfrac{g_t}{\sqrt{S_t}+\epsilon},其中S_t = \beta S_{t-1} + (1-\beta) g_t^2 \]
这里,我们主要使用二阶矩 来对每个参数实现"自适应学习率",用平滑梯度平方测定梯度"幅度"并以此来缩小大梯度,放大小梯度。同样,如果你有些遗忘,详细的解释在这里:RMSprop
看这两个算法的公式,有没有发现,他们更改的位置完全不冲突?
- Momentum 把和学习率相乘的梯度改为平滑梯度。
- RMSprop 用平滑梯度的平方做开方当成梯度的分母。
就像之前说的,Adam 的参数更新公式相比创新,它更像合成:
\[\theta_{t+1}= \theta_t - \alpha \cdot \frac{\hat{v}_t}{\sqrt{\hat{S}_t} + \epsilon} \]
很明显,Adam 把上面两者结合起来,同时应用一阶矩和二阶矩 ,既有稳定方向,又能自动调节不同参数的学习率。
还是打个比方:Momentum就像告诉往哪走的指南针,而RMSprop像告诉怎么走的地图,二者相加就成了Adam这个智能导航。
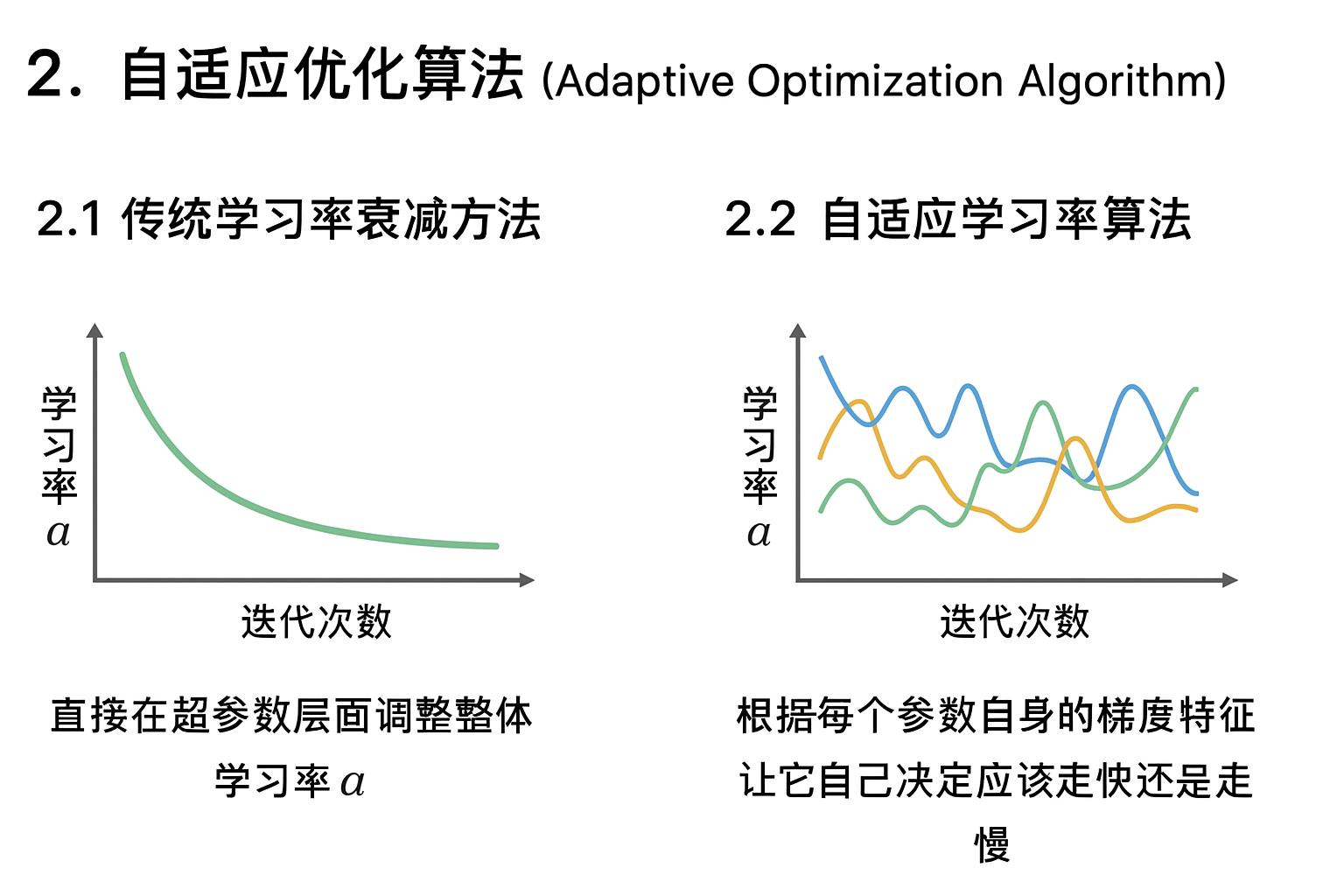
2. 自适应优化算法(Adaptive Optimization Algorithm)
2.1传统学习率衰减方法
我们在之前学习率衰减部分学过各种"学习率衰减"方法,比如 指数衰减 、分段衰减 、1/t 衰减 。
而这些方法的共同点是:直接在超参数层面调整整体学习率 α。
也就是说,它们的核心思路是:用一个全局函数控制所有参数的步长变化,每次迭代时整个模型的学习率一起变小或变大。
而我们也在RMSprop部分了解了这种对所有参数应用统一学习率的不足。
2.2 自适应学习率算法
实际上,RMSprop,Adam 算法被统称为自适应学习率算法或者自适应优化算法。(还有一种叫AdaGrad,是改进前的RMSprop,几乎不再使用,所以就不提了)
"自适应学习率(Adaptive Learning Rate)"指的并不是简单地去改超参数 α, 而是根据每个参数自身的梯度特征,让它自己决定应该走快还是走慢。
换句话说,这类算法不是"直接改 α" , 而是"在更新时给每个参数都乘上一个自适应比例系数"。
从而形成一种 "隐式学习率" 的变化机制。
就像我们这两篇所介绍的,这种机制让算法能在不同维度上动态分配更新强度,即使学习率 α 是固定的,也能实现"局部自调节"的效果。
因此,Adam 不需要额外的衰减函数,也能自动学会该快时快、该慢时慢。
本周的理论部分就到此为止,下一篇的实操部分,我们就看看这些优化算法相比原来的普通梯度下降法,在性能上有多少提升。
3."人话版"总结
| 概念 | 原理 | 比喻 |
|---|---|---|
| Adam | 同时计算一阶矩(方向)和二阶矩(幅度),并做偏差修正。综合Momentum的"稳方向"和RMSprop的"调步长"。 | 像个智能导航系统:Momentum告诉你该往哪走,RMSprop告诉你怎么走得稳,两者合体成了"自动驾驶模式"。 |
| 传统学习率衰减 | 通过全局公式(如指数衰减、1/t衰减等)手动让整个模型学习率逐步下降。 | 像定时器:无论路况怎样,到点就自动降速。 |
| 自适应学习率算法 | 不再改α本身,而是让每个参数在更新时都带上"自调节比例",实现隐式学习率。 | 就像每个车轮都能独立判断地面情况,自主控制转速,整体协调而智能地前进。 |