解密“混合专家模型” (MoE) 的全部魔法

解密"混合专家模型" (MoE) 的全部魔法

在当今大语言模型 (LLM) 的竞赛中，您一定听说过 GPT-4、Mixtral 8x7B 这样的"巨无霸"。它们之所以能在保持惊人性能的同时实现高效推理，背后都指向一个共同的架构------MoE (Mixture of Experts) 混合专家模型。

MoE 不是一个全新的概念，它的思想最早在 1991 年（Jacobs, Hinton 等）就被提出。但直到这个"大模型"时代，它"稀疏激活"的核心思想才真正得以大放异彩。

这篇博客将汇总我们之前的所有讨论，带您从 MoE 的核心思想出发，一路深入到它最底层的训练"黑魔法"，彻底搞懂它高效运转的全部秘密。

篇章一：MoE 的核心思想------"分而治之"

什么是 MoE？一个"专家委员会"的比喻

要理解 MoE，我们可以先想象一个"专家委员会"：

传统的"密集"模型 (Dense Model)：

就像一个试图精通所有领域的"通才"。当遇到任何问题时，这个"通才"必须调动他全部的知识（模型的全部参数）来思考。当模型变得非常大时，这个过程会极其缓慢且耗费资源。
MoE 混合专家模型：

就像一个拥有多名"专科医生"的医院。医院里有心脏科专家、神经科专家、骨科专家等（这就是 Experts）。
1. 当一个病人（输入数据 ，例如一个 Token）到来时，会先去"分诊台"（这就是 Gating Network 或 Router）。
2. "分诊台"会快速判断："你这个问题，看起来最需要心脏科和神经科的专家会诊。"
3. 于是，只有这两位专家被"激活"（Active）并参与工作。其他专家则继续"休息"，不消耗计算资源。
4. 最后，"分诊台"将两位专家的诊断结果（输出）汇总起来，给出一个综合的答案。

MoE 的"魔法"：总参数 vs 激活参数

MoE 架构（尤其是"稀疏 MoE"）解决了大型模型的一个核心痛点：如何在不增加计算成本的前提下，极大地扩展模型的知识容量（参数量） 。

这就引出了两个关键概念：

总参数量 (Total Parameters)：

模型所有专家参数的总和。这代表了模型的"知识库"有多庞大。
- 例如，Mixtral 8x7B 拥有 8 个 7B（70亿）参数的专家，总参数量约 47B。
激活参数量 (Active Parameters)：

处理单个 Token 时，实际参与计算的参数量。这决定了模型的"推理速度"。
- Mixtral 8x7B 在处理每个 Token 时，只激活 8 个专家中的 2 个 (Top-K=2)。
- 因此，它实际的计算量大约只和一个 12B-14B 的密集模型相当。

结论： MoE 允许我们拥有一个 47B 量级的"知识库"，但享受的却是 14B 量级的"推理速度"！

为什么只选 K=2（少数）而不是 K=8（全部）？

这正是 MoE 的全部意义所在。

激活 K=2 (稀疏激活) ：用 14B 的计算成本，撬动 47B 的知识库。 （高效）
激活 K=8 (密集激活) ：用 47B 的计算成本，撬动 47B 的知识库。 （昂贵）

如果你激活了全部 8 个专家，MoE 就退化成了一个普通的、巨大且缓慢的密集模型，完全丧失了其计算优势。

篇章二：MoE 的架构与实践

核心组件（一）：专家 (Experts)

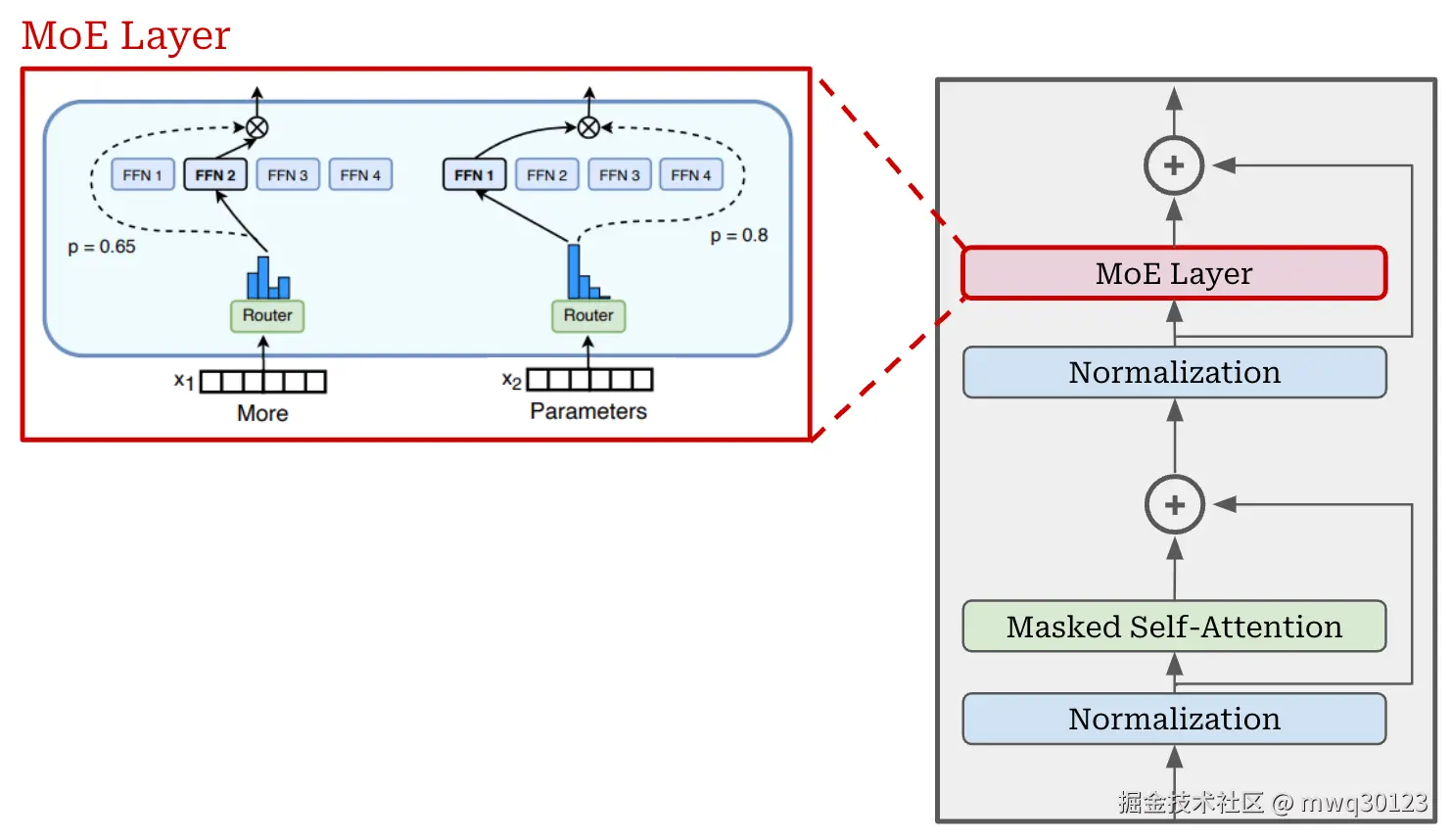
在 Transformer 架构中，MoE 通常被应用在 FFN（前馈网络）层。这意味着"专家"本身通常就是多个独立的 FFN 网络。

在训练过程中，每个 FFN 专家会逐渐"学会"处理特定类型的数据、模式或概念。比如，一个专家可能擅长处理编程代码，另一个专家可能擅长处理诗歌。

核心组件（二）：门控网络 (Gating Network)

这是 MoE 的"大脑"和"调度中心"。它的理论基础是**"可学习的加权平均" (Learnable Weighted Averaging)**。

其工作流程如下：

打分 (Logits) ：门控网络（通常是一个小型的线性层）接收一个 Token，并为 <math xmlns="http://www.w3.org/1998/Math/MathML"> N N </math>N 个专家中的每一个都打一个"分数"。
归一化 (Softmax) ：使用 Softmax 函数将这些分数转换成"权重"或"概率"（总和为 1）。例如 [0.1, 0.05, 0.6, ..., 0.25]。
Top-K 选择：选择权重最高的 K 个（例如 K=2）专家。
加权输出：模型只激活这 K 个专家，并将它们的输出，按照 Gating 给出的权重进行"加权平均"，得到最终的输出。

Gating 网络和专家是一起训练的。Gating 会学会"如何分配权重"才能让模型的总损失最小。久而久之，它就学会了："遇到代码，找 3 号和 7 号专家。"

MoE 与 CNN 多通道的类比

这是一个非常好的类比，能帮我们深入理解其机制：

相似之处 (专业分工) ：
- CNN 的不同通道 (Channel) 提取不同特征（如边缘、颜色）。
- MoE 的不同专家 (Expert) 处理不同概念（如代码、法律）。
根本区别 (密集 vs 稀疏) ：
- CNN 是"密集"的 ：所有通道都会被同时激活和计算。
- MoE 是"稀疏"的 ：只有被选中的 Top-K 专家被激活。如果 Gating 认为这个 Token 是代码，它就只去激活"代码专家"。

MoE 模型的生命周期

MoE 架构贯穿了模型的所有阶段：

预训练 (Pre-training) ：MoE 诞生和学习的阶段。
- 专家在海量数据中"专业化"。
- Gating 网络学会如何"路由"。
- （关键）模型学会"负载均衡"。
微调 (Fine-tuning) ：MoE 适应和优化的阶段。
- 在特定任务（如问答）上，Gating 和 Experts 的参数被进一步调整和优化。
生成/推理 (Inference) ：MoE 展现优势的阶段。
- Gating 为每一个 生成的 Token 实时动态地选择 Top-K 专家。
- 这就是我们享受到"稀疏激活"带来高速推理的时刻。

篇章三：MoE 训练的"黑魔法"------负载均衡 (Load Balancing)

我们已经知道了 MoE 的美好，但它在训练中有一个致命问题： "明星专家"问题。

如果没有约束，Gating 网络可能会很快发现 3 号专家"比较聪明"，于是它"偷懒"地把所有任务都交给 3 号。这会导致：

明星专家 (Star Expert) ：3 号专家"过劳"，见识了所有数据。
摸鱼专家 (Lazy Experts) ：其他 7 个专家"无所事事"，它们的参数完全得不到训练，被白白浪费。

为了解决这个问题，MoE 引入了一个"惩罚"机制，称为负载均衡 (Load Balancing) 。

<math xmlns="http://www.w3.org/1998/Math/MathML"> L balance L_{\text{balance}} </math>Lbalance：惩罚明星专家的"辅助损失"

这个机制的理念非常像"权重衰减 (Weight Decay)"------它通过施加"惩罚"来防止模型过分依赖某几个专家。

在训练时，模型的总损失 (Total Loss) 由两部分组成：

<math xmlns="http://www.w3.org/1998/Math/MathML"> L total = L main + α ⋅ L balance L_{\text{total}} = L_{\text{main}} + \alpha \cdot L_{\text{balance}} </math>Ltotal=Lmain+α⋅Lbalance

<math xmlns="http://www.w3.org/1998/Math/MathML"> L main L_{\text{main}} </math>Lmain：主损失，即"预测是否准确"。
<math xmlns="http://www.w3.org/1998/Math/MathML"> L balance L_{\text{balance}} </math>Lbalance：辅助损失（即"惩罚项"） ，用于衡量"路由是否均衡"。
<math xmlns="http://www.w3.org/1998/Math/MathML"> α \alpha </math>α：一个超参数，用于控制"惩罚"的力度。

<math xmlns="http://www.w3.org/1998/Math/MathML"> L balance L_{\text{balance}} </math>Lbalance 的结算公式与过程

这个"惩罚"的计算，是在**"批次" (Batch)** 级别上进行的。在训练时，GPU 会一次性处理一个批次，例如 [32, 1024]，即总共 32,768 个 Token。

负载均衡损失的经典公式如下：

<math xmlns="http://www.w3.org/1998/Math/MathML"> L balance = N ⋅ ∑ i = 1 N f i ⋅ P i L_{\text{balance}} = N \cdot \sum_{i=1}^{N} f_i \cdot P_i </math>Lbalance=N⋅∑i=1Nfi⋅Pi

我们来拆解这几个关键变量（在一个批次的 32,768 个 Token 中）：

<math xmlns="http://www.w3.org/1998/Math/MathML"> N N </math>N ：专家的总数量（例如 8）。
<math xmlns="http://www.w3.org/1998/Math/MathML"> G G </math>G (概率矩阵)：

Gating 网络为所有 32,768 个 Token 并行计算出的"路由概率"。这是一个 [32768, 8] 的矩阵。
<math xmlns="http://www.w3.org/1998/Math/MathML"> D D </math>D (调度掩码)：

对 G 矩阵的每一行（每个 Token）执行 Top-K（例如 K=2）操作，得到一个"硬决策"的 0/1 掩码。这是一个 [32768, 8] 的矩阵，每一行恰好有 2 个 1。
<math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi (平均路由概率)：

Gating 网络的"意向"。

它是 G 矩阵第 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 列的平均值。代表在这个批次中，Gating 希望分配给专家 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 的平均概率。
<math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi (任务分配比例)：

专家的"实际工作量"。

它是 D 矩阵第 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 列的平均值。代表在这个批次中，专家 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 实际被分配了百分之多少的 Token。

结算：

<math xmlns="http://www.w3.org/1998/Math/MathML"> L balance L_{\text{balance}} </math>Lbalance 通过将"实际工作量"( <math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi) 和"意向"( <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi) 相乘，来计算每个专家的"不均衡贡献"，最后汇总得出总惩罚。

篇章四：MoE 训练的"天才诡计"------不可微分的 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi

您在深入思考后，一定已经发现了几个最棘手的技术问题。这些问题是 MoE 训练的精髓所在。

疑问一：如果 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i = 0 f_i = 0 </math>fi=0（摸鱼专家），惩罚从何而来？

您是对的！在一个批次中，如果一个专家一次都没被选中，它的 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i = 0 f_i = 0 </math>fi=0，因此它的贡献 f_i * P_i = 0。

惩罚并非来自"摸鱼专家"，而是来自"明星专家"！

"明星专家"的 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi 都很高，导致它的 f_i * P_i 贡献值极大。
这使得总的 <math xmlns="http://www.w3.org/1998/Math/MathML"> L balance L_{\text{balance}} </math>Lbalance 惩罚非常高。
优化器为了降低这个惩罚，会强迫 Gating 网络降低"明星专家"的 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi 。
（关键） Gating 使用的是 Softmax（总和为1）。你从"明星"那里剥夺的概率，必须"重新分配"给其他人。
"摸鱼专家"的 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi 就这样被动地提高了！ 在下一个批次中，它被选中的概率就变大了。

疑问二：为什么不干脆只平衡 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi（概率）？

既然 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi（硬决策）只是 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi（软概率）的结果，为什么不直接设计一个损失函数（例如 <math xmlns="http://www.w3.org/1998/Math/MathML"> L = variance ( P i ) L = \text{variance}(P_i) </math>L=variance(Pi)）来平衡 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi 就行了？

答案是：因为 Top-K 这个"硬决策"操作是不可微分的 (Non-Differentiable)。

这是理解 MoE 训练的终极障碍，也是它最天才的"诡计"。

什么叫"不可微分"？

想象一个"步阶函数"（Step Function）： <math xmlns="http://www.w3.org/1998/Math/MathML"> x > 0 x > 0 </math>x>0 时 <math xmlns="http://www.w3.org/1998/Math/MathML"> y = 1 y=1 </math>y=1， <math xmlns="http://www.w3.org/1998/Math/MathML"> x ≤ 0 x \le 0 </math>x≤0 时 <math xmlns="http://www.w3.org/1998/Math/MathML"> y = 0 y=0 </math>y=0。

在 <math xmlns="http://www.w3.org/1998/Math/MathML"> x = 0 x=0 </math>x=0 处，它是一个"跳跃"，斜率（导数/梯度）不存在。在 <math xmlns="http://www.w3.org/1998/Math/MathML"> x ≠ 0 x \ne 0 </math>x=0 的地方，它又是"平的"，斜率=0。

机器学习的反向传播依赖"梯度"来更新参数。如果梯度为 0 或不存在，优化器就"瞎了"，不知道该往哪走。
<math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi 为什么不可微分？

<math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi 是通过 Top-K 这个"硬比较"操作得来的。

Gating 网络对参数做出的微小改变（例如 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi 从 0.40 变成 0.41），可能完全不会改变 Top-K 的决策结果。

Gating 的参数 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ \theta </math>θ 变了，但 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi 却"纹丝不动"。

这意味着 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi 相对于 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ \theta </math>θ 的梯度 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ f i Δ θ = 0 \frac{\Delta f_i}{\Delta \theta} = 0 </math>ΔθΔfi=0。

如果损失函数只基于 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi，梯度将无法回传，Gating 网络永远无法被训练！

<math xmlns="http://www.w3.org/1998/Math/MathML"> L balance L_{\text{balance}} </math>Lbalance 的"天才诡计"： <math xmlns="http://www.w3.org/1998/Math/MathML"> f i ⋅ ∇ P i f_i \cdot \nabla P_i </math>fi⋅∇Pi

<math xmlns="http://www.w3.org/1998/Math/MathML"> L balance = N ⋅ ∑ ( f i ⋅ P i ) L_{\text{balance}} = N \cdot \sum (f_i \cdot P_i) </math>Lbalance=N⋅∑(fi⋅Pi) 这个公式的天才之处在于，它如何"绕过"了不可微分的障碍。

在反向传播计算梯度时，它运用了一个"技巧"：

<math xmlns="http://www.w3.org/1998/Math/MathML"> ∇ L balance ∝ f i ⋅ ∇ P i \nabla L_{\text{balance}} \propto f_i \cdot \nabla P_i </math>∇Lbalance∝fi⋅∇Pi

我们知道 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi 本身是不可微分的（梯度为 0），但 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi（来自 Softmax）是可微分的。
<math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi 在这里被"伪装"成一个**"常数缩放因子"**（即"惩罚力度"）。
梯度 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∇ L \nabla L </math>∇L 实际上是沿着可微分的 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∇ P i \nabla P_i </math>∇Pi 这条路回传的。

直白地说：

优化器："Gating 网络，我要惩罚你的 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi（概率输出）。"

惩罚的力度 = 你"实际"分配给这个专家的工作量 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi。

对于"明星专家"： <math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi 很高，惩罚力度 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i ⋅ ∇ P i f_i \cdot \nabla P_i </math>fi⋅∇Pi 就非常大。
对于"摸鱼专家"： <math xmlns="http://www.w3.org/1998/Math/MathML"> f i = 0 f_i = 0 </math>fi=0，惩罚力度 <math xmlns="http://www.w3.org/1998/Math/MathML"> 0 ⋅ ∇ P i = 0 0 \cdot \nabla P_i = 0 </math>0⋅∇Pi=0。

这就是 MoE 训练的全部秘密：它利用"不可微分"的实际工作量 <math xmlns="http://www.w3.org/1998/Math/MathML"> f i f_i </math>fi 作为权重，去惩罚"可微分"的路由意向 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi，再通过 Softmax 的内在机制，被动地"提拔"那些"摸鱼"的专家。

总结

MoE（混合专家模型）是一种绝妙的架构，它通过稀疏激活（激活 Top-K）实现了"巨大知识库"（总参数）和"极高推理速度"（激活参数）的完美平衡。

为了使其有效工作，它在训练中必须使用负载均衡 （ <math xmlns="http://www.w3.org/1998/Math/MathML"> L balance L_{\text{balance}} </math>Lbalance）来防止"明星专家"问题。

而负载均衡的核心，是一个天才般的"梯度诡计"，它巧妙地绕过了 Top-K 决策的"不可微分"障碍，成功地训练了 Gating 网络。

希望这篇博客能帮您彻底理清 MoE 的所有脉络！