1 题目
给出二叉搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键小于节点键的节点。
- 节点的右子树仅包含键大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意: 本题和 1038. 从二叉搜索树到更大和树 - 力扣(LeetCode) 相同
示例 1:
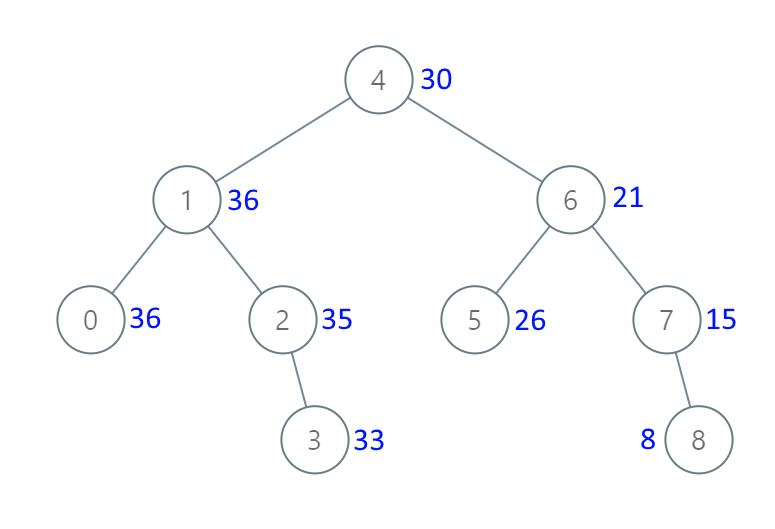
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]示例 2:
输入:root = [0,null,1]
输出:[1,null,1]示例 3:
输入:root = [1,0,2]
输出:[3,3,2]示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
2 代码实现
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
int sum = 0 ;
void traverse(TreeNode* root){
if (root == nullptr){
return;
}
traverse(root -> right );
sum += root -> val;
root-> val = sum;
traverse(root -> left);
}
public:
TreeNode* convertBST(TreeNode* root) {
sum = 0;
traverse(root);
return root;
}
};详细解题步骤:把二叉搜索树转换为累加树
一、问题分析
题目要求:将二叉搜索树(BST)转换为累加树,使每个节点的新值等于原树中所有「大于或等于该节点原值」的节点值之和。
核心特性:二叉搜索树的中序遍历(左→根→右)结果是升序序列。例如,对于 BST:
bash
4
/ \
1 6中序遍历为 [1,4,6](升序)。
关键思路 :要计算「大于或等于当前节点值的和」,需要从大到小处理节点(先处理大值,再累加小值)。因此,我们可以采用反向中序遍历 (右→根→左),遍历顺序为 [6,4,1](降序),便于累计总和。
二、算法设计
-
反向中序遍历:遍历顺序为「右子树 → 根节点 → 左子树」,确保从大到小访问节点。
-
累加和计算 :用一个变量
sum记录已访问节点的累加和(这些节点值均 ≥ 当前节点值)。遍历到当前节点时,将其原值加入sum,再将当前节点的新值设为sum。 -
原地修改 :直接修改原树节点的
val属性,无需新建节点,节省内存空间。
问题理解
题目要求把二叉搜索树(BST)转换为累加树,每个节点的新值等于原树中所有大于或等于该节点原值的节点值之和。
关键突破口:二叉搜索树的特性是中序遍历(左→根→右)结果为升序序列。
而我们需要的是 "大于或等于当前值的和",所以可以反过来遍历 ------右→根→左(降序序列),这样就能从大到小处理节点,方便累加计算。
核心代码实现
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
int sum = 0; // 用于累计"大于等于当前节点值"的总和
// 反向中序遍历:右子树 → 根节点 → 左子树
void reverseInorder(TreeNode* node) {
if (node == nullptr) return; // 空节点直接返回
// 1. 先遍历右子树(右子树的所有节点值都比当前节点大)
reverseInorder(node->right);
// 2. 处理当前节点:把当前值加入总和,再更新当前节点值为总和
sum += node->val;
node->val = sum;
// 3. 再遍历左子树(左子树的所有节点值都比当前节点小)
reverseInorder(node->left);
}
public:
TreeNode* convertBST(TreeNode* root) {
sum = 0; // 每次调用重置总和
reverseInorder(root); // 执行反向中序遍历并修改节点值
return root;
}
};详细讲解
1. 为什么用反向中序遍历?
- 二叉搜索树的特性:对于任意节点,右子树所有节点值 > 该节点值 ,左子树所有节点值 < 该节点值。
- 要计算 "大于或等于当前节点值的和",需要先处理所有比当前节点大的节点(右子树),再处理当前节点,最后处理比它小的节点(左子树)。
- 反向中序遍历(右→根→左)的顺序,正好是从大到小访问节点,完美匹配需求。
2. 代码执行流程(以示例 1 为例)
示例 1 输入树结构:
bash
4
/ \
1 6
/ \ / \
0 2 5 7
/ \
3 8- 初始
sum = 0,开始反向中序遍历:- 最右节点是 8 →
sum += 8(sum=8)→ 节点 8 的值改为 8。 - 回到 7 →
sum +=7(sum=15)→ 节点 7 的值改为 15。 - 回到 6 的右子树处理完,处理 6 →
sum +=6(sum=21)→ 节点 6 的值改为 21。 - 处理 6 的左子树 5 →
sum +=5(sum=26)→ 节点 5 的值改为 26。 - 回到根节点 4 →
sum +=4(sum=30)→ 节点 4 的值改为 30。 - 处理 4 的左子树 2 的右子树 3 →
sum +=3(sum=33)→ 节点 3 的值改为 33。 - 回到 2 →
sum +=2(sum=35)→ 节点 2 的值改为 35。 - 处理 1 的右子树完毕,处理 1 →
sum +=1(sum=36)→ 节点 1 的值改为 36。 - 处理 1 的左子树 0 →
sum +=0(sum=36)→ 节点 0 的值改为 36。
- 最右节点是 8 →
最终得到的累加树与示例输出一致。
3. 关键逻辑
- 用
sum变量累计已经处理过的节点值(这些值都≥当前节点值)。 - 每个节点在被处理时,先将自己的值加入
sum,再把自己的新值设为sum(此时sum已经包含了所有≥自己的值)。
4. 复杂度分析
- 时间复杂度:O (n),每个节点只被访问一次。
- 空间复杂度:O (h),h 是树的高度(递归调用栈的深度),最坏情况(链状树)为 O (n)。
通过这种方法,只需一次遍历就能完成转换,充分利用了二叉搜索树的特性,高效且易于理解。
【最后是怎么输出的?原地修改吗?】
是的,代码中采用的是原地修改的方式,最终直接返回修改后的原树的根节点,不需要额外构造新的二叉树。
具体说明:
-
原地修改的含义 :在遍历过程中,我们直接修改了原二叉树中每个节点的
val值(通过node->val = sum),没有创建任何新的TreeNode对象。树的结构(节点之间的连接关系,即left和right指针)保持不变,仅节点存储的值被更新。 -
返回结果的方式 :函数
convertBST的返回值是root(原树的根节点),但此时root指向的树已经是修改后的累加树。外部调用者可以通过这个根节点访问整个修改后的树,进而按需求输出(例如层序遍历、前序遍历等)。
为什么可以原地修改?
- 题目只要求转换后每个节点的值满足 "大于或等于原节点值的和",对树的结构没有要求(不需要新建节点,保持原结构即可)。
- 原地修改可以节省内存空间(无需额外存储新树的节点),且实现简单(直接修改原节点的值即可)。
举例说明输出过程:
以示例 1 为例,修改后的树结构不变,但每个节点的值已更新:
bash
30 (原4)
/ \
36 21 (原1和6)
/ \ / \
36 35 26 15 (原0、2、5、7)
/ \
33 8 (原3和8)当需要输出结果时,只需从根节点30开始,按题目要求的格式(通常是层序遍历,空节点用null表示)遍历并打印即可,例如示例 1 的输出为:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]。
总结:代码通过原地修改原树节点的值完成转换,最终返回原树的根节点,外部通过遍历该根节点即可得到题目要求的输出。
二叉搜索树心法(特性篇) | labuladong 的算法笔记
几行代码解释了很简洁的思想,以前的我肯定不相信自己能做这样的题目,算法只要有心学,不会那么可怕,慢慢来,比较快。