文章目录
- [1. Bagging](#1. Bagging)
-
- [1.1 核心思想](#1.1 核心思想)
- [1.2 二元分类](#1.2 二元分类)
- [1.3 相关性的影响](#1.3 相关性的影响)
- [1.4 随机森林(Random Forest)](#1.4 随机森林(Random Forest))
- [1.5 小结](#1.5 小结)
- [2. Boosting](#2. Boosting)
-
- [2.1 AdaBoost 算法](#2.1 AdaBoost 算法)
-
- [2.1.1 弱学习器(Weak Learner)](#2.1.1 弱学习器(Weak Learner))
-
- [2.1.1.1 决策桩(Decision Stumps)](#2.1.1.1 决策桩(Decision Stumps))
- [2.1.2 AdaBoost 算法的具体步骤](#2.1.2 AdaBoost 算法的具体步骤)
-
- [2.1.2.1 AdaBoost 算法中权重调整](#2.1.2.1 AdaBoost 算法中权重调整)
- [2.1.3 AdaBoost算法的示例](#2.1.3 AdaBoost算法的示例)
- [2.1.4 最小化训练误差](#2.1.4 最小化训练误差)
- [2.1.5 AdaBoost 算法的泛化误差(generalization error)](#2.1.5 AdaBoost 算法的泛化误差(generalization error))
- [2.1.6 作为拟合加性模型(Additive Models)](#2.1.6 作为拟合加性模型(Additive Models))
-
- [2.1.6.1 指数损失函数](#2.1.6.1 指数损失函数)
- [2.1.7 AdaBoost 算法小结](#2.1.7 AdaBoost 算法小结)
- [2.2 小结](#2.2 小结)
- [3. 集成学习](#3. 集成学习)
1. Bagging
我们上一章说到偏差方差分解。
下图用飞镖的比喻来形象地解释了偏差(Bias)和方差(Variance)对模型预测性能的影响。
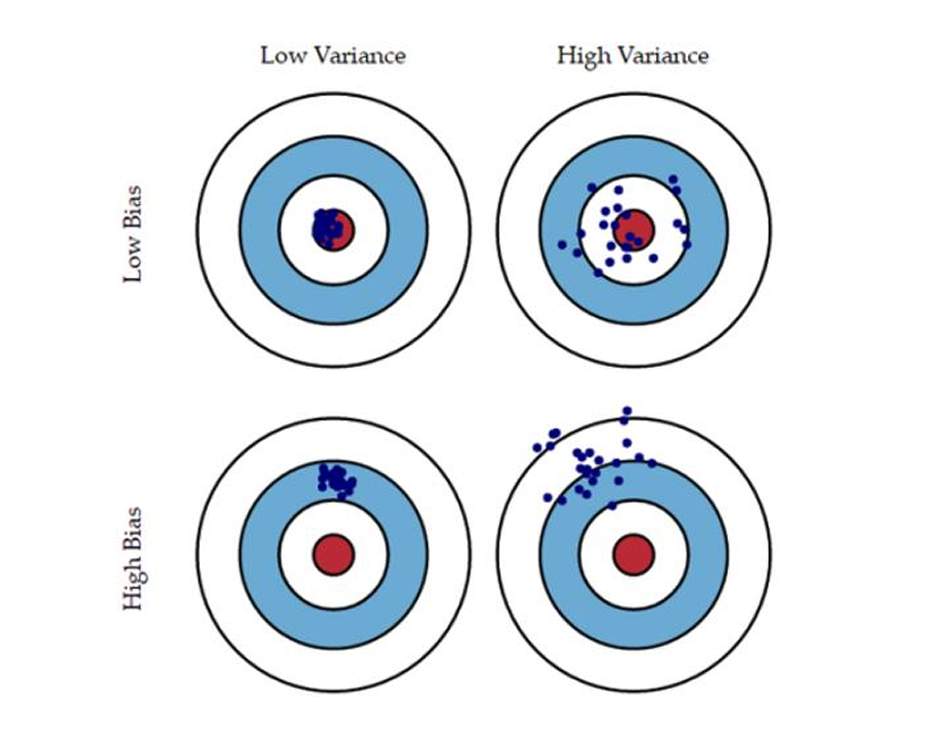
四个飞镖靶,每个靶上都有不同分布的飞镖点,代表模型在不同情况下的预测结果。
左上角(低偏差,低方差):飞镖点集中在靶心附近,表示模型预测准确且稳定。
右上角(低偏差,高方差):飞镖点分布分散但都靠近靶心,表示模型预测稳定但不够准确。
左下角(高偏差,低方差):飞镖点集中在偏离靶心的位置,表示模型预测不准确但稳定。
右下角(高偏差,高方差):飞镖点分散且偏离靶心,表示模型预测既不准确也不稳定。
我们现在讨论如何优化偏差方差。
我们可以训练多个模型,每个模型给出一个预测值 Y i Y_i Yi,然后把它们的预测结果取平均,得到最终预测 y ˉ = 1 m ∑ i = 1 m Y i \bar{y} = \frac{1}{m}\sum_{i=1}^{m} Y_i yˉ=m1∑i=1mYi
这对我们模型的"期望损失"三项(Bayes误差、偏差、方差)有什么影响?
Bayes误差(不可约误差)不变,因为这是数据本身的噪声,我们做什么模型都改不了。
偏差不变,因为每个模型的期望预测值是一样的,平均之后期望也没变。
E [ y ˉ ] = E [ 1 m ∑ i = 1 m Y i ] = 1 m ∑ i = 1 m E [ Y i ] \mathbb{E}[\bar{y}] = \mathbb{E}\!\left[\frac{1}{m}\sum_{i=1}^{m} Y_i\right] = \frac{1}{m}\sum_{i=1}^{m}\mathbb{E}[Y_i] E[yˉ]=E[m1∑i=1mYi]=m1∑i=1mE[Yi]
换句话说,Bagging 不会让一个"错的模型"变成对的,它只是把多个"同样偏"的模型平均一下。
方差减少了,因为我们在对多个独立同分布的预测结果做平均。
V a r ( y ˉ ) = V a r ( 1 m ∑ i = 1 m Y i ) = 1 m 2 ∑ i = 1 m V a r ( Y i ) = 1 m V a r ( Y i ) \mathrm{Var}(\bar{y}) = \mathrm{Var}\!\left(\frac{1}{m}\sum_{i=1}^{m} Y_i\right) = \frac{1}{m^2}\sum_{i=1}^{m}\mathrm{Var}(Y_i) = \frac{1}{m}\mathrm{Var}(Y_i) Var(yˉ)=Var(m1∑i=1mYi)=m21∑i=1mVar(Yi)=m1Var(Yi)
平均独立随机变量会让方差按 1 / m 1/m 1/m的比例下降。
1.1 核心思想
在实际中,数据分布 p s a m p l e p_{sample} psample往往是有限的或采样成本很高,所以每次都从真实分布中独立采样新数据集来训练模型是非常浪费数据的。
那为什么不只用一个数据集,然后通过有放回地重复采样来"模拟"多个数据集呢?
这就是 Bagging(Bootstrap Aggregating) 的核心思想。
你有一个大小为 n n n的训练集D。
从这个数据集中有放回地随机采样 n n n个样本,生成一个新的数据集(也叫 bootstrap 样本)。
重复这个过程 m m m次,得到 m m m个"新"数据集。
在每个数据集上训练一个模型,最后平均(或投票)它们的预测结果。
Bootstrap 是统计学中最重要的思想之一。
当数据量 n n n越来越大时,从原始数据集中有放回采样得到的分布 P D P_D PD会越来越接近真实的数据分布 P s a m p l e P_{sample} Psample。
下图展示了一个 n = 7 n=7 n=7, m = 3 m=3 m=3的例子。
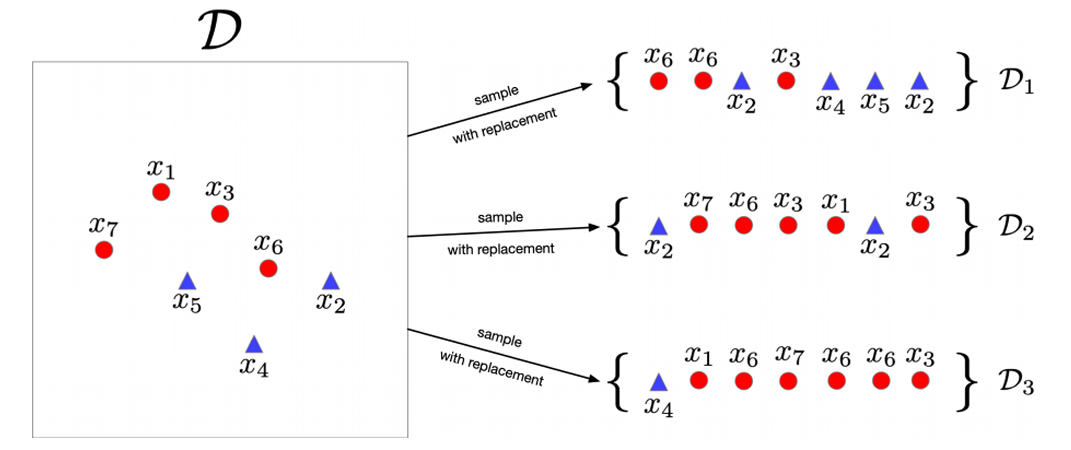
从同一份数据有放回地抽取7条样本,生成 3 份彼此不同的'新'训练集,用来训练 3 个模型,再平均/投票。
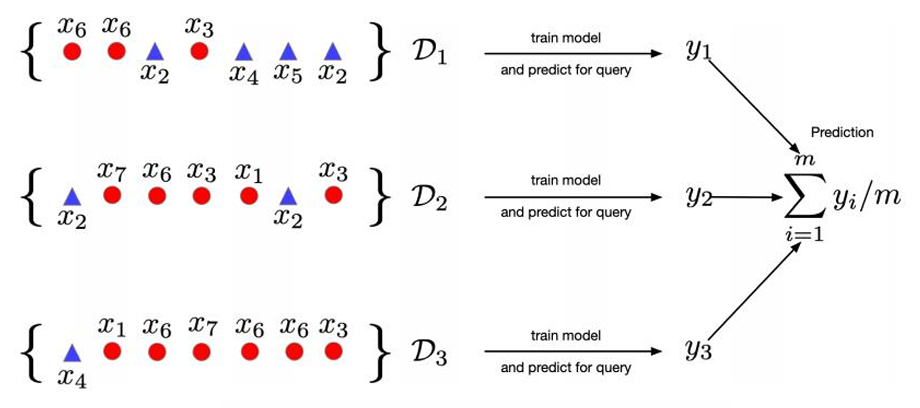
我们用这 3 组训练集分别训练了 3 个模型,我们把同一条查询样本 x 喂给每个模型 , 得到 3 个预测值,取平均(回归)或投票(分类)作为最终输出。
Bagging 不改变单个模型的偏差(bias),但它会"偷偷"扩大模型的假设空间,使得最终集成出来的预测函数,可能不再是原来单个模型能表示的那一类函数。
下面给出例子。
输入 x x x在 [ − 3 , 3 ] [-3, 3] [−3,3]均匀分布,目标 t t t服从标准正态噪声。
假设空间只是一条斜率受限的直线( w w w被锁在 [ − 1 , 1 ] [-1, 1] [−1,1])。
每次从真实分布采样一个数据集,用线性回归拟合出一条 w x wx wx,斜率 w w w会随数据波动而在 [ − 1 , 1 ] [-1, 1] [−1,1]内变化。

把 1000 条这样的直线逐点取平均(即 Bagging 的期望预测)。
结果这条"平均直线"不再是直线。它可能带曲率,跳出了原来"只能是一条 w x wx wx"的集合 H H H。
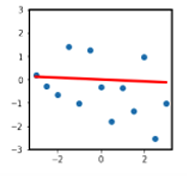
这个现象在用决策树、神经网络等非线性分类器时更明显:单棵决策树只能划轴平行线,平均后却可得到任意分段边界。
1.2 二元分类
在二分类任务里,无论基分类器输出的是"概率"还是"硬投票(0/1)",Bagging 都可以把它们的预测先平均,再统一做 0.5 阈值判断;这种"平均后再决定"的策略,往往比单个模型的准确度更高。
每个基分类器给出属于类别1的概率 z i ∈ [ 0 , 1 ] z_i \in [0,1] zi∈[0,1] ,
然后我们把这些概率取平均 z bagged = 1 m ∑ i = 1 m z i z_{\text{bagged}} = \frac{1}{m}\sum_{i=1}^{m} z_i zbagged=m1∑i=1mzi,
如果其概率超过0.5则属于类别1,
y bagged = I ( z bagged > 0.5 ) y_{\text{bagged}} = \mathbb{I}(z_{\text{bagged}} > 0.5) ybagged=I(zbagged>0.5)
如果我们的基分类器的结果只有0或1,即 y i ∈ { 0 , 1 } y_i \in \{0,1\} yi∈{0,1}
同样可以先平均这些 0/1,再判断。
y ˉ = 1 m ∑ i = 1 m y i \bar{y} = \frac{1}{m}\sum_{i=1}^{m} y_i yˉ=m1∑i=1myi
y bagged = I ( y ˉ > 0.5 ) y_{\text{bagged}} = \mathbb{I}(\bar{y} > 0.5) ybagged=I(yˉ>0.5)
这样"平均后再决定"的集成模型,往往比单个模型更强。
1.3 相关性的影响
如果 m m m个模型的预测完全独立,方差会按 1 / m 1/m 1/m线性下降。
但Bagging里每个模型用的数据都来自同一份原始训练集D,只是有放回地重采样,因此训练出的模型彼此正相关( ρ > 0 ρ > 0 ρ>0)。
相关性越高,平均带来的方差缩减收益越小。
Var ( 1 m ∑ i = 1 m Y i ) = σ 2 m ( 1 − ρ ) + σ 2 ρ \operatorname{Var}\!\left(\frac{1}{m}\sum_{i=1}^{m}Y_{i}\right) = \frac{\sigma^{2}}{m}(1 - \rho) + \sigma^{2}\rho Var(m1∑i=1mYi)=mσ2(1−ρ)+σ2ρ,
其中 σ 2 \sigma^2 σ2:单个模型预测的方差
ρ \rho ρ:模型间预测结果的相关系数
m m m:基模型数量
当 ρ = 0 ρ = 0 ρ=0(完全独立)⇒ 方差 = σ 2 / m σ²/m σ2/m,最大降幅。
当 ρ = 1 ρ = 1 ρ=1(完全相关)⇒ 方差 = σ 2 σ² σ2,毫无降幅(跟用一个模型一样)。
实际 0 < ρ < 1 0 < ρ < 1 0<ρ<1,所以方差只能部分下降,下降比例由 ρ ρ ρ决定。
1.4 随机森林(Random Forest)
随机森林 = 把决策树做 Bagging,再加一个去相关(decorrelate)的小技巧。
每次分裂节点时,先从全部特征里随机抽 𝑑 𝑑 d个候选特征,然后只在这 𝑑 𝑑 d个里选最优划分。
这个 𝑑 𝑑 d是超参,常用默认值:
分类: 𝑑 = √ p 𝑑 = √p d=√p
回归: 𝑑 = p / 3 𝑑 = p/3 d=p/3( p p p为总特征数)
作用:
让各棵树"长得不一样",降低树间相关性 ρ ρ ρ,从而把 Bagging 的方差缩减效果再放大。
随机森林大概是最强黑盒算法------几乎不用调参就能跑得不错。也是 Kaggle 比赛里最常用的算法之一(尤其是结构化表格数据)。
1.5 小结
Bagging 通过平均预测结果来减少过拟合。
通过集成多个模型,即使这些模型本身已经表现不错,也可以进一步提升性能。
但是在平方误差的情况下不减少偏差。 Bagging 主要通过减少方差来提高模型的泛化能力,但对模型的偏差影响不大。
分类器之间仍然存在相关性。 由于所有模型都是基于同一数据集的不同子集训练的,它们之间可能存在一定的相关性,这限制了方差的进一步减少。
随机森林解决方案:增加更多的随机性。 随机森林通过在每个决策节点随机选择特征来进一步减少模型之间的相关性,从而提高集成的效果。
简单的混合(所有成员权重相等)。 Bagging 中的模型权重是相等的,这可能不是最优的,因为不同模型的性能可能差异很大。
如果成员非常不同(例如,不同的算法,不同的数据源等),我们通常可以通过使用有原则的加权集成方法获得更好的结果。 当集成的模型差异较大时,根据模型的性能给予不同的权重可能会更有效。
接下来要讲的Boosting可以看作是一种加权集成方法,它强烈地去相关集成成员。 Boosting 通过迭代地训练模型,每个新模型都试图纠正前一个模型的错误,从而实现模型之间的去相关,并根据模型的表现给予不同的权重。
2. Boosting
顺序训练分类器,每次训练时专注于前一个分类器分类错误的样本,通过这种方式逐步提升整体模型的性能。
由于每个模型都专注于不同的错误样本,它们的预测结果之间的相关性降低,这有助于提高集成模型的泛化能力。
为了专注于特定样本,Boosting 使用加权的训练集。每个样本在训练集中的权重会根据其被前一个模型分类的正确与否进行调整。被错误分类的样本权重会增加,从而在后续模型中得到更多的关注。
传统的错误分类率 1 N ∑ n = 1 N I [ h ( x ( n ) ) ≠ t ( n ) ] \frac{1}{N}\sum_{n=1}^{N} \mathbb{I}[h(x^{(n)}) \neq t^{(n)}] N1∑n=1NI[h(x(n))=t(n)]将每个训练样本视为等权重。这里, I [ h ( x ( n ) ) ≠ t ( n ) ] \mathbb{I}[h(x^{(n)}) \neq t^{(n)}] I[h(x(n))=t(n)]是指示函数,当模型 h h h对样本 x ( n ) x^{(n)} x(n)预测不等于真实标签时,其值为1,否则为0。
我们可以为不同的样本分配不同的成本(或权重)来学习分类器。
分类器会"更努力"地学习那些具有更高成本的样本。
于是我们将原来的成本函数 ∑ n = 1 N w ( n ) I [ h ( x ( n ) ) ≠ t ( n ) ] \sum_{n=1}^{N} w^{(n)} \mathbb{I}[h(x^{(n)}) \neq t^{(n)}] ∑n=1Nw(n)I[h(x(n))=t(n)]修改为 ∑ n = 1 N w ( n ) = 1 \sum_{n=1}^{N} w^{(n)} = 1 ∑n=1Nw(n)=1,这里, w ( n ) w^{(n)} w(n)是样本 n n n的权重。
通常要求每个权重 w ( n ) > 0 w^{(n)}>0 w(n)>0 且所有权重之和为 1 1 1。
2.1 AdaBoost 算法
AdaBoost 的关键步骤如下:
- 在每次迭代中,通过给被错误分类的样本(即数据点)分配更大的权重来重新加权训练样本。
- 基于重新加权的样本训练一个新的基础分类器。
- 将其以适当的权重添加到分类器集成中。
- 多次重复这个过程。
基础分类器的要求:
- 需要最小化加权误差。
- 集成可能会变得非常大,因此基础分类器必须快速。事实证明,任何所谓的弱学习器/分类器都可以。
单独来看,弱学习器可能具有高偏差(欠拟合)。通过让每个分类器专注于之前的错误,AdaBoost 减少了偏差。
2.1.1 弱学习器(Weak Learner)
弱学习器是一种学习算法,它输出的假设(例如分类器)的性能略好于随机猜测。例如,在二分类问题中,它以0.51的概率正确预测标签。
我们对计算效率高的弱学习器感兴趣。
例如决策树是一种常见的弱学习器,因为它可以快速地进行训练和预测。
更简单的是决策桩(Decision Stump),它是一种只有一个分裂的决策树。
正式定义:弱可学习性(weak learnability)的正式定义涉及到一些量化指标,例如"对于数据的任何分布",并且其保证仅以概率形式成立。
这意味着在理论上,弱学习器能够在一定的概率下,对于任何数据分布,找到一个略好于随机猜测的分类器。
2.1.1.1 决策桩(Decision Stumps)
决策桩是最简单的决策树,由水平和垂直的半空间组成。
如下图所示。
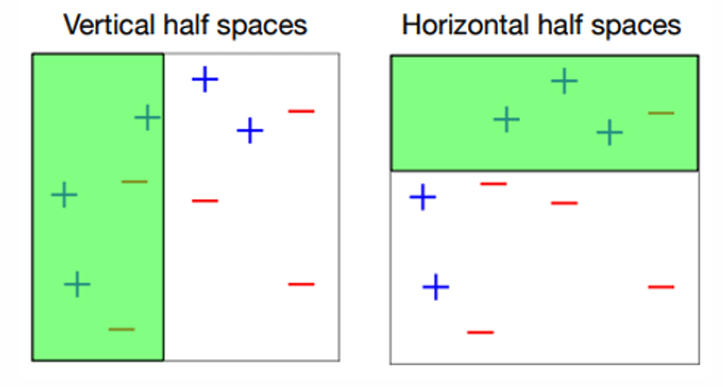
左边是垂直半空间(Vertical half spaces):基于特征值的垂直分割,例如 x 2 ≤ 2 x_2≤2 x2≤2或 x 2 > 2 x_2>2 x2>2。
右边是水平半空间(Horizontal half spaces):基于特征值的水平分割,例如 x 1 ≤ 2 x_1≤2 x1≤2或 x 1 > 2 x_1>2 x1>2。
单个弱分类器无法使训练误差变得很小。
但如果能保证它的表现略好于随机猜测,即分类器 h h h根据给定的权重 w = w 1 , ... , w N \mathbf{w} = w_1, \ldots, w_N w=w1,...,wN的加权误差最多是 1 2 − γ \frac{1}{2} - \gamma 21−γ(其中 γ > 0 \gamma > 0 γ>0),那么使用AdaBoost结合这些弱分类器可以给我们一个通用函数逼近器。
上次我们使用信息增益作为分裂标准。在使用AdaBoost的决策桩时,我们通常使用"GINI不纯度",这(大致上)选择直接最小化误差的分裂。
GINI不纯度是一种衡量数据集不纯度的方法,它倾向于选择那些能够最大程度减少分类错误的分裂。
我们回顾之前学习的知识。
输入数据集 D N \mathcal{D}_N DN包含 N N N个样本,每个样本由特征向量 x ( n ) \mathbf{x}^{(n)} x(n)和对应的标签 t ( n ) t^{(n)} t(n)组成。这里标签的取值是 -1 或 +1 与之前的 0,1 不同。但这只是为了方便记号,两者在本质上是等价的。
D N = { x ( n ) , t ( n ) } n = 1 N where t ( n ) ∈ { − 1 , + 1 } \mathcal{D}N = \{\mathbf{x}^{(n)}, t^{(n)}\}{n=1}^N \text{ where } t^{(n)} \in \{-1, +1\} DN={x(n),t(n)}n=1N where t(n)∈{−1,+1}
分类器或假设 h h h是一个函数,它将输入特征向量 x x x映射到输出标签 −1 或 +1。
h : x → { − 1 , + 1 } h: \mathbf{x} \rightarrow \{-1, +1\} h:x→{−1,+1}
0-1 损失函数用于衡量分类器的预测结果与真实标签之间的差异。
I [ h ( x ( n ) ) ≠ t ( n ) ] = 1 2 ( 1 − h ( x ( n ) ) ⋅ t ( n ) ) \mathbb{I}[h(\mathbf{x}^{(n)}) \neq t^{(n)}] = \frac{1}{2}(1 - h(\mathbf{x}^{(n)}) \cdot t^{(n)}) I[h(x(n))=t(n)]=21(1−h(x(n))⋅t(n))
其中 I [ h ( x ( n ) ) ≠ t ( n ) ] \mathbb{I}[h(\mathbf{x}^{(n)}) \neq t^{(n)}] I[h(x(n))=t(n)]是指示函数,当预测结果与真实标签不同时,其值为 1,否则为 0。
等号后面的式子也可以用来计算 0-1 损失,其中 h ( x ( n ) ) ⋅ t ( n ) ) h(\mathbf{x}^{(n)}) \cdot t^{(n)}) h(x(n))⋅t(n))是预测标签与真实标签的点积。
2.1.2 AdaBoost 算法的具体步骤
输入:输入数据集 D N \mathcal{D}_N DN包含 N N N个样本,每个样本由特征向量 x ( n ) \mathbf{x}^{(n)} x(n)和对应的标签 t ( n ) t^{(n)} t(n)组成。
D N = { x ( n ) , t ( n ) } n = 1 N where t ( n ) ∈ { − 1 , + 1 } \mathcal{D}N = \{\mathbf{x}^{(n)}, t^{(n)}\}{n=1}^N \text{ where } t^{(n)} \in \{-1, +1\} DN={x(n),t(n)}n=1N where t(n)∈{−1,+1}
一个返回分类器 h h h的分类过程,例如最佳决策桩,从一个分类器集合 H H H中选择,例如所有可能的决策桩。
以及迭代次数 T T T。
输出:最终的分类器。
步骤:
-
初始化样本权重:
w ( n ) = 1 N w^{(n)} = \frac{1}{N} \quad w(n)=N1对于所有 n = 1 , ... , N n=1,\ldots,N n=1,...,N -
对于 t = 1 , ... , T t=1,\ldots,T t=1,...,T
-
使用加权数据训练一个分类器 h t h_t ht: h t ← arg min h ∈ H ∑ n = 1 N w ( n ) I { h ( x ( n ) ) ≠ t ( n ) } h_t \leftarrow \arg\min_{h \in \mathcal{H}} \sum_{n=1}^{N} w^{(n)} \mathbb{I}\{h(\mathbf{x}^{(n)}) \neq t^{(n)}\} ht←argminh∈H∑n=1Nw(n)I{h(x(n))=t(n)}
-
计算加权错误 err t \text{err}t errt: err t = ∑ n = 1 N w ( n ) I { h t ( x ( n ) ) ≠ t ( n ) } ∑ n = 1 N w ( n ) \text{err}t = \frac{\sum{n=1}^{N} w^{(n)} \mathbb{I}\{h_t(\mathbf{x}^{(n)}) \neq t^{(n)}\}}{\sum{n=1}^{N} w^{(n)}} errt=∑n=1Nw(n)∑n=1Nw(n)I{ht(x(n))=t(n)}
-
计算分类器系数 α t \alpha_t αt: α t = 1 2 log 1 − err t err t ( \alpha_t = \frac{1}{2} \log \frac{1 - \text{err}_t}{\text{err}_t} \quad ( αt=21logerrt1−errt(其中 err t ∈ ( 0 , ∞ ) ) \text{err}_t \in (0, \infty)) errt∈(0,∞))
-
更新数据权重 w ( n ) w^{(n)} w(n): w ( n ) ← w ( n ) exp ( − α t t ( n ) h t ( x ( n ) ) ) w^{(n)} \leftarrow w^{(n)} \exp(-\alpha_t t^{(n)} h_t(\mathbf{x}^{(n)})) \quad w(n)←w(n)exp(−αtt(n)ht(x(n)))等价于 w ( n ) exp ( 2 α t I { h t ( x ( n ) ) ≠ t ( n ) } ) ) w^{(n)} \exp(2\alpha_t \mathbb{I}\{h_t(\mathbf{x}^{(n)}) \neq t^{(n)}\})) w(n)exp(2αtI{ht(x(n))=t(n)}))
- 返回最终的分类器 H ( x ) H(\mathbf{x}) H(x): H ( x ) = sign ( ∑ t = 1 T α t h t ( x ) ) H(\mathbf{x}) = \text{sign}\left(\sum_{t=1}^{T} \alpha_t h_t(\mathbf{x})\right) H(x)=sign(∑t=1Tαtht(x)),它是所有弱分类器的加权和的符号函数。
2.1.2.1 AdaBoost 算法中权重调整
我们最后最终分类器 H ( x ) H(\mathbf{x}) H(x): H ( x ) = sign ( ∑ t = 1 T α t h t ( x ) ) H(\mathbf{x}) = \text{sign}\left(\sum_{t=1}^{T} \alpha_t h_t(\mathbf{x})\right) H(x)=sign(∑t=1Tαtht(x))是所有弱分类器 h t ( x ) h_t(\mathbf{x}) ht(x)的加权和的符号函数,其中 α t \alpha_t αt是第 t t t个弱分类器的系数。
这个系数 α t = 1 2 log 1 − err t err t \alpha_t = \frac{1}{2} \log \frac{1 - \text{err}_t}{\text{err}_t} \quad αt=21logerrt1−errt由第 t t t个弱分类器的错误率 err t \text{err}_t errt决定。
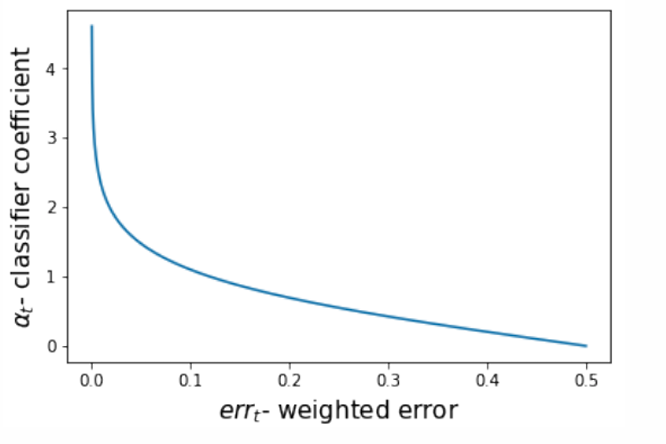
- 当 err t \text{err}_t errt接近 0 时, α t \alpha_t αt较大,这意味着分类器在训练数据上的错误率很低,因此它在最终分类器中的影响较大。
- 当 err t \text{err}_t errt接近 0.5 时, α t \alpha_t αt较小,这意味着分类器在训练数据上的错误率较高,因此它在最终分类器中的影响较小。
同样样本权重 w ( n ) w^{(n)} w(n)根据第 t t t个弱分类器对样本 x ( n ) \mathbf{x}^{(n)} x(n)的分类结果进行更新:
w ( n ) ← w ( n ) exp ( 2 α t I { h t ( x ( n ) ) ≠ t ( n ) } ) w^{(n)} \leftarrow w^{(n)} \exp(2\alpha_t \mathbb{I}\{h_t(\mathbf{x}^{(n)}) \neq t^{(n)}\}) w(n)←w(n)exp(2αtI{ht(x(n))=t(n)})
- 如果 h t ( x ( n ) ) ≠ t ( n ) h_t(\mathbf{x}^{(n)}) \neq t^{(n)} ht(x(n))=t(n)(即样本被错误分类),则权重增加,这意味着在后续迭代中,这个样本会被赋予更多的关注。
- 如果 h t ( x ( n ) ) = t ( n ) h_t(\mathbf{x}^{(n)}) = t^{(n)} ht(x(n))=t(n)(即样本被正确分类),则权重减少,这意味着在后续迭代中,这个样本会被赋予较少的关注。
2.1.3 AdaBoost算法的示例
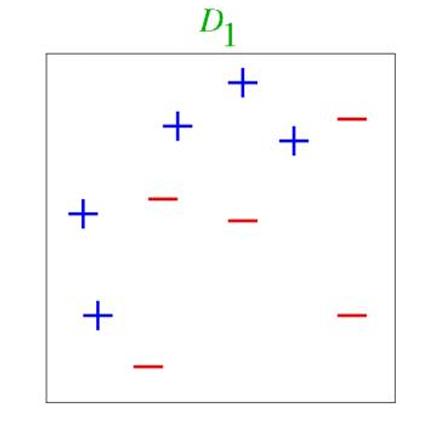
这是用于训练的数据集,标记为 D 1 D_1 D1。
第一轮迭代:
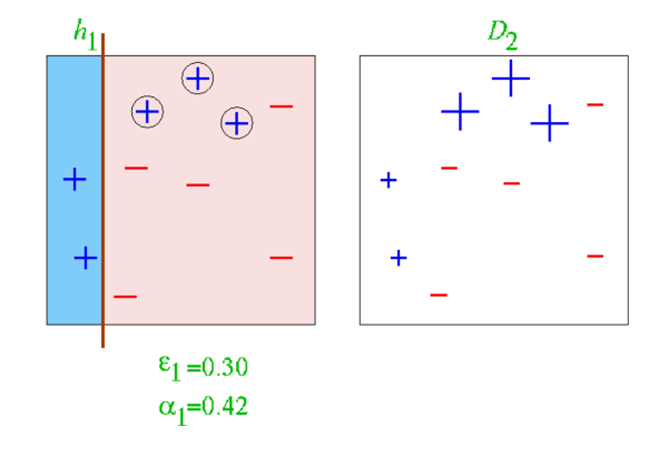
左图显示了第一个弱分类器 h 1 h_1 h1的决策边界,它将数据分为两个区域(蓝色和粉色),每个区域内的样本被分类为同一类别。
右图显示了根据第一个弱分类器 h 1 h_1 h1的错误分类结果重新加权后的数据集 D 2 D_2 D2,其中被错误分类的样本(位于决策边界另一侧的样本)在后续迭代中将被赋予更高的权重。
第一个弱分类器的错误率为 ϵ 1 = 0.30 \epsilon_1 = 0.30 ϵ1=0.30
第一个弱分类器的权重为 α 1 = 1 2 log 1 − ϵ 1 ϵ 1 = 0.42 \alpha_1 = \frac{1}{2} \log \frac{1 - \epsilon_1}{\epsilon_1}=0.42 α1=21logϵ11−ϵ1=0.42
我们现在一步步执行:
-
权重初始化 w = ( 1 10 , ... , 1 10 ) \mathbf{w} = \left(\frac{1}{10}, \ldots, \frac{1}{10}\right) w=(101,...,101),表示所有样本初始权重相等。
-
训练分类器:使用初始权重 w \mathbf{w} w训练第一个弱分类器 h 1 h_1 h1。
-
计算错误率: err 1 = ∑ i = 1 10 w i I { h 1 ( x ( i ) ) ≠ t ( i ) } ∑ i = 1 10 w i = 3 10 \text{err}1 = \frac{\sum{i=1}^{10} w_i \mathbb{I}\{h_1(\mathbf{x}^{(i)}) \neq t^{(i)}\}}{\sum_{i=1}^{10} w_i} = \frac{3}{10} err1=∑i=110wi∑i=110wiI{h1(x(i))=t(i)}=103,表示有 3 个样本被错误分类。
-
计算分类器系数: α 1 = 1 2 log 1 − err 1 err 1 = 1 2 log 1 0.3 − 1 ≈ 0.42 \alpha_1 = \frac{1}{2} \log \frac{1 - \text{err}_1}{\text{err}_1} = \frac{1}{2} \log \frac{1}{0.3} - 1 \approx 0.42 α1=21logerr11−err1=21log0.31−1≈0.42。
-
最终分类器: H ( x ) = sign ( α 1 h 1 ( x ) ) H(\mathbf{x}) = \text{sign}(\alpha_1 h_1(\mathbf{x})) H(x)=sign(α1h1(x)),最终分类器是第一个弱分类器的加权结果。
第二轮迭代:
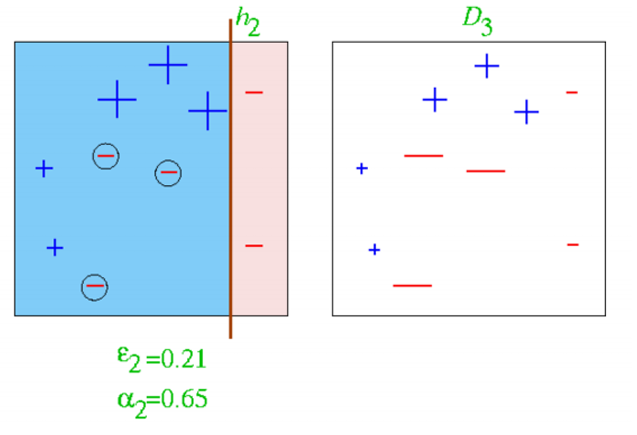
左图显示了第二个弱分类器 h 2 h_2 h2的决策边界,它专注于第一轮中被错误分类的样本(蓝色区域)。
右图显示了根据第一个弱分类器 h 2 h_2 h2的错误分类结果重新加权后的数据集 D 3 D_3 D3,其中被错误分类的样本(位于决策边界另一侧的样本)在后续迭代中将被赋予更高的权重。
第二个弱分类器的错误率为 ϵ 2 = 0.21 \epsilon_2 = 0.21 ϵ2=0.21。
第二个弱分类器的权重为 α 2 = 0.65 \alpha_2 = 0.65 α2=0.65。
我们现在一步步执行:
- 权重更新 w = updated weights \mathbf{w} = \text{updated weights} w=updated weights,所有样本权重根据第一轮的结果进行了更新。
- 使用更新后的权重 w \mathbf{w} w 训练第二个弱分类器 h 2 h_2 h2。
- 计算错误率: err 2 = ∑ i = 1 10 w i I { h 2 ( x ( i ) ) ≠ t ( i ) } ∑ i = 1 10 w i = 0.21 \text{err}2 = \frac{\sum{i=1}^{10} w_i \mathbb{I}\{h_2(\mathbf{x}^{(i)}) \neq t^{(i)}\}}{\sum_{i=1}^{10} w_i} = 0.21 err2=∑i=110wi∑i=110wiI{h2(x(i))=t(i)}=0.21。
- 计算分类器系数: α 2 = 1 2 log 1 − err 2 err 2 = 1 2 log 1 0.21 ≈ 0.66 \alpha_2 = \frac{1}{2} \log \frac{1 - \text{err}_2}{\text{err}_2} = \frac{1}{2} \log \frac{1}{0.21} \approx 0.66 α2=21logerr21−err2=21log0.211≈0.66。
- 最终分类器: H ( x ) = sign ( α 1 h 1 ( x ) + α 2 h 2 ( x ) ) H(\mathbf{x}) = \text{sign}(\alpha_1 h_1(\mathbf{x}) + \alpha_2 h_2(\mathbf{x})) H(x)=sign(α1h1(x)+α2h2(x)),最终分类器是前两个弱分类器的加权结果。
第三轮迭代:
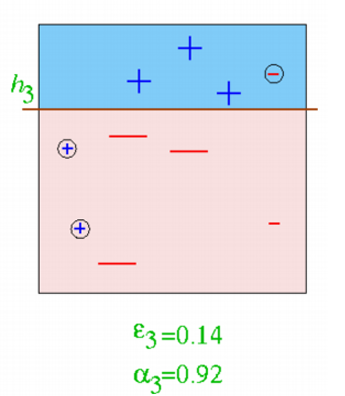
上图显示了第三个弱分类器 h 3 h_3 h3的决策边界,它专注于第二轮中被错误分类的样本。
第三个弱分类器的错误率为 ϵ 3 = 0.14 \epsilon_3 = 0.14 ϵ3=0.14。
第三个弱分类器的权重为 α 3 = 0.92 \alpha_3 = 0.92 α3=0.92。
我们现在一步步执行:
- 权重更新 w = updated weights \mathbf{w} = \text{updated weights} w=updated weights,所有样本权重根据第二轮的结果进行了更新。
- 使用更新后的权重 w \mathbf{w} w 训练第三个弱分类器 h 3 h_3 h3。
- 计算错误率: err 3 = ∑ i = 1 10 w i I { h 3 ( x ( i ) ) ≠ t ( i ) } ∑ i = 1 10 w i = 0.14 \text{err}3 = \frac{\sum{i=1}^{10} w_i \mathbb{I}\{h_3(\mathbf{x}^{(i)}) \neq t^{(i)}\}}{\sum_{i=1}^{10} w_i} = 0.14 err3=∑i=110wi∑i=110wiI{h3(x(i))=t(i)}=0.14。
- 计算分类器系数: α 3 = 1 2 log 1 − err 3 err 3 = 1 2 log 1 0.14 ≈ 0.91 \alpha_3 = \frac{1}{2} \log \frac{1 - \text{err}_3}{\text{err}_3} = \frac{1}{2} \log \frac{1}{0.14} \approx 0.91 α3=21logerr31−err3=21log0.141≈0.91。
- 最终分类器: H ( x ) = sign ( α 1 h 1 ( x ) + α 2 h 2 ( x ) + α 3 h 3 ( x ) ) H(\mathbf{x}) = \text{sign}(\alpha_1 h_1(\mathbf{x}) + \alpha_2 h_2(\mathbf{x}) + \alpha_3 h_3(\mathbf{x})) H(x)=sign(α1h1(x)+α2h2(x)+α3h3(x)),最终分类器是前三个弱分类器的加权结果。
所以我们得到最终的分类器如下图所示。
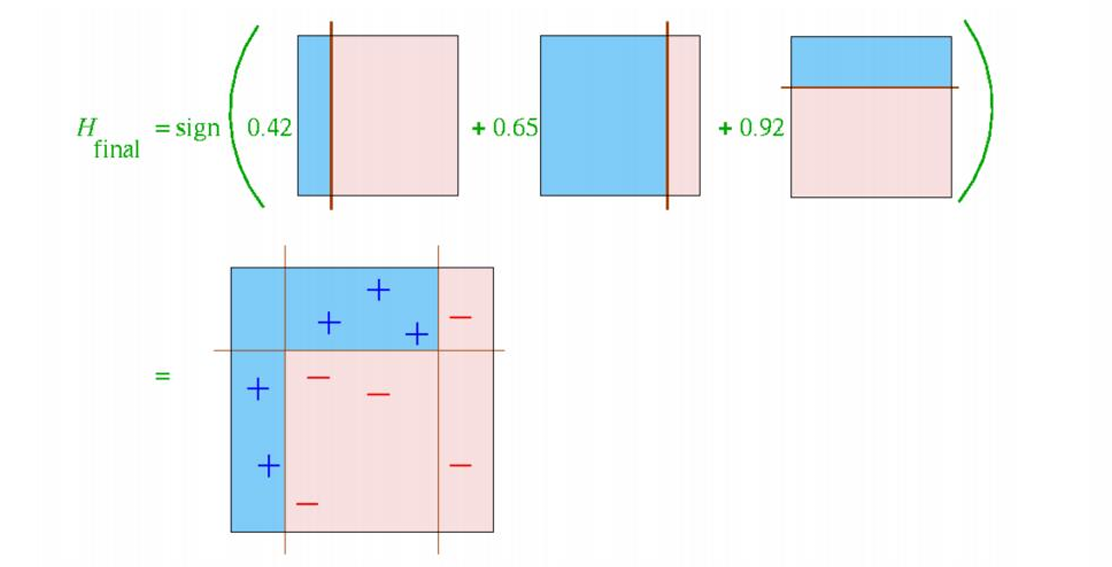
H final = sign ( α 1 h 1 ( x ) + α 2 h 2 ( x ) + α 3 h 3 ( x ) ) H_\text{final}= \text{sign}(\alpha_1 h_1(\mathbf{x}) + \alpha_2 h_2(\mathbf{x}) + \alpha_3 h_3(\mathbf{x})) Hfinal=sign(α1h1(x)+α2h2(x)+α3h3(x))
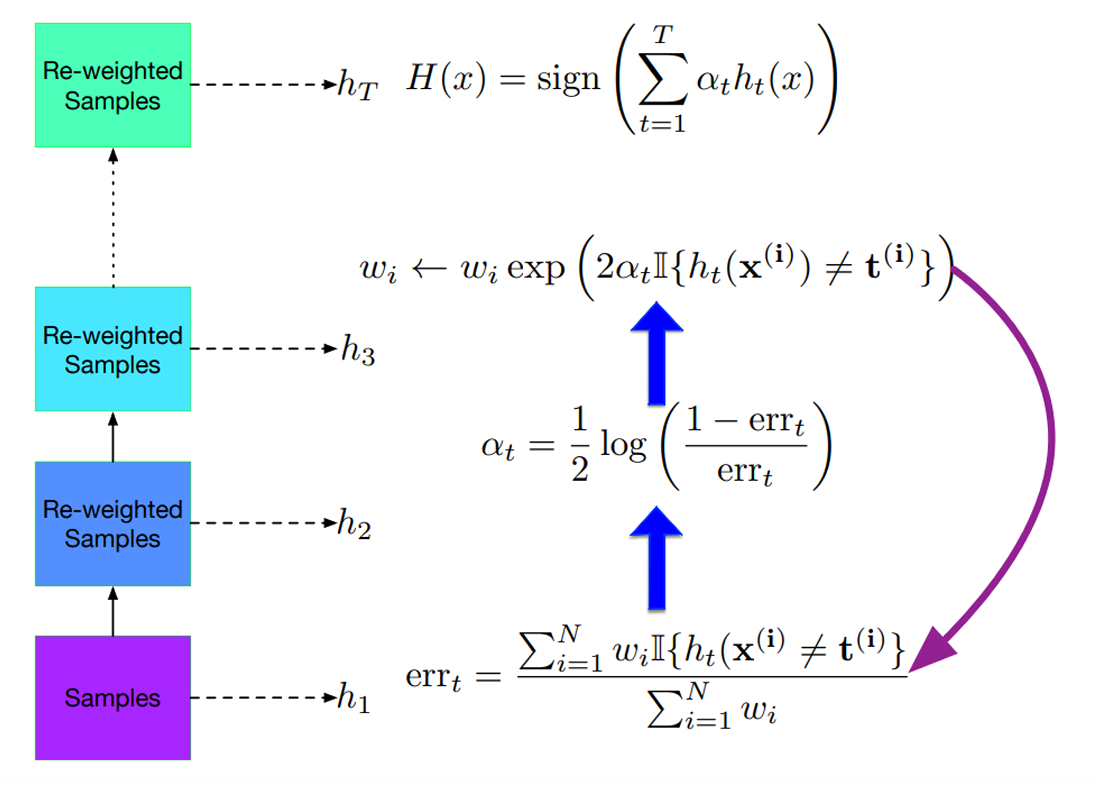
所以我们的步骤就是用弱分类器分类,然后计算错误率,然后根据错误率计算弱分类器的权重,再根据弱分类器的权重计算样本权重。最后将所有弱分类器加权和得到最终分类器。
下图又展现了一个例子。
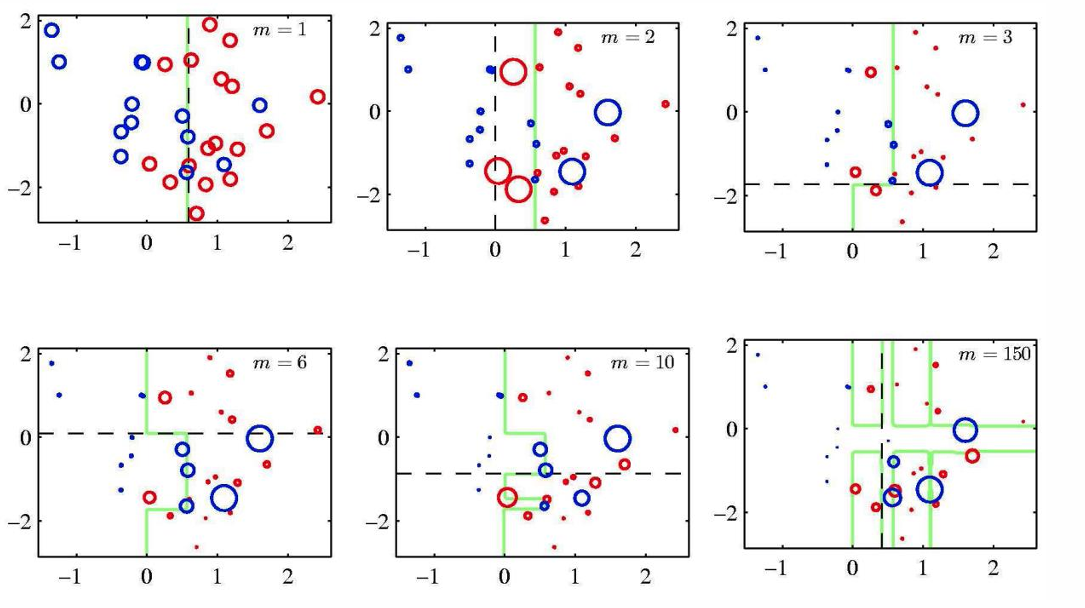
每个图展示了在不同数量的弱分类器( m m m)训练完成后,最近一个弱分类器的决策边界(虚线黑色),以及集成分类器的决策边界(绿色)。
随着弱分类器数量的增加,集成分类器的决策边界变得更加复杂和精确,能够更好地捕捉数据中的模式。
2.1.4 最小化训练误差
下面的定理展示了 AdaBoost 算法的一个重要性质:在每次迭代中,如果每个弱学习器都比随机猜测好 γ γ γ,那么最终集成模型的训练误差会以几何级数快速下降。这种快速的收敛性是 AdaBoost 算法的一个显著优点,使其在实践中非常有效。
定理:假设在 AdaBoost 的每次迭代中,WeakLearn 返回的假设(分类器)的错误率 err t ≤ 1 2 − γ \text{err}t \leq \frac{1}{2} - \gamma errt≤21−γ对于所有 t = 1 , ... , T t=1,\ldots,T t=1,...,T且 γ > 0 \gamma > 0 γ>0。输出假设 H ( x ) = sign ( ∑ t = 1 T α t h t ( x ) ) H(\mathbf{x})=\text{sign}\left(\sum{t=1}^{T} \alpha_t h_t(\mathbf{x})\right) H(x)=sign(∑t=1Tαtht(x))的训练误差最多为:
L N ( H ) = 1 N ∑ i = 1 N I { H ( x ( i ) ) ≠ t ( i ) } ≤ exp ( − 2 γ 2 T ) L_N(H) = \frac{1}{N} \sum_{i=1}^{N} \mathbb{I}\{H(\mathbf{x}^{(i)}) \neq t^{(i)}\} \leq \exp(-2\gamma^2 T) LN(H)=N1∑i=1NI{H(x(i))=t(i)}≤exp(−2γ2T)
其中 L N ( H ) L_N(H) LN(H)是输出假设 H H H在训练集上的错误率。
这是在简化的假设下得出的,即每个弱学习器都比随机预测器好 γ γ γ。
这被称为几何级数收敛,它非常快。
2.1.5 AdaBoost 算法的泛化误差(generalization error)
AdaBoost 的训练误差(损失)收敛到零。那么 H H H的测试误差呢?
换句话说,虽然 AdaBoost 的训练误差可以降到很低,甚至接近于零,但这是否意味着它在测试集上的表现也同样优秀?
随着我们添加更多的弱分类器,整体分类器 H H H变得更加"复杂"。我们预计更复杂的分类器会过拟合。
如果运行 AdaBoost 足够长的时间,它实际上可能会过拟合。
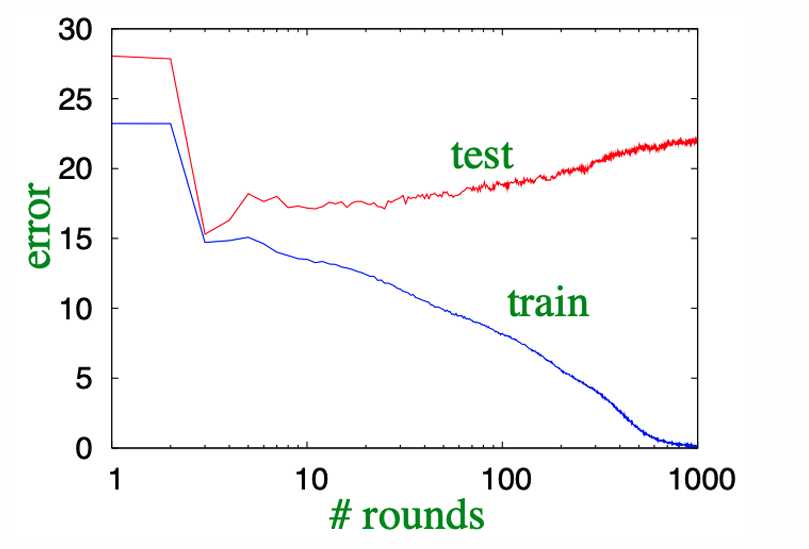
图中展示了训练误差和测试误差随迭代次数(rounds)的变化趋势:
蓝色曲线表示训练误差,随着迭代次数的增加,训练误差逐渐降低,最终趋近于零。
红色曲线表示测试误差,开始时测试误差也降低,但在某个点之后开始上升,显示出过拟合的迹象。
有时候,即使训练误差已经降到零,测试误差仍然会继续下降。
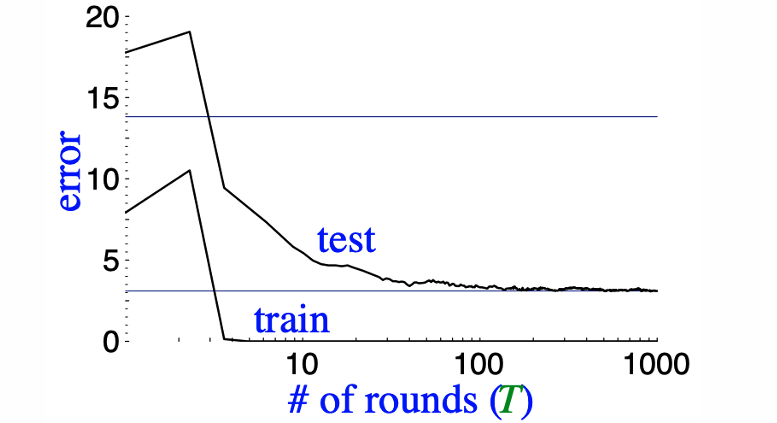
图中展示了训练误差和测试误差随迭代次数(rounds)的变化趋势:
蓝色曲线表示训练误差,随着迭代次数的增加,训练误差迅速下降并趋近于零。
红色曲线表示测试误差,开始时测试误差也下降,但在训练误差降到零后,测试误差继续下降,然后趋于平稳。
在接下来的讨论中,我们将介绍一种不同的方法或理论框架来解释 AdaBoost 的工作原理,这将解答它如何在训练误差为零后仍然能够改善测试误差的原因。
2.1.6 作为拟合加性模型(Additive Models)
接下来,我们将 AdaBoost 解释为拟合加性模型的一种方式。
考虑一个假设类 H \mathcal{H} H,其中每个 h i h_i hi映射到 { − 1 , + 1 } \{-1, +1\} {−1,+1},即 h i ∈ H h_i \in \mathcal{H} hi∈H。这些是"弱学习器",在这种情况下,它们也被称为基(bases)。
一个包含 m m m项的加性模型由下式给出:
H m ( x ) = ∑ i = 1 m α i h i ( x ) H_m(\mathbf{x}) = \sum_{i=1}^{m} \alpha_i h_i(\mathbf{x}) Hm(x)=∑i=1mαihi(x),其中 ( α 1 , ⋯ , α m ) ∈ R m (\alpha_1, \cdots, \alpha_m) \in \mathbb{R}^m (α1,⋯,αm)∈Rm。
注意到我们正在取基分类器 h i ( x ) h_i (x) hi(x)的线性组合,就像在提升中一样。 还要注意与我们在线性回归和神经网络中看到的特征映射(或基扩展)的联系。
加性模型(Additive Models)的分阶段训练方法是AdaBoost 算法背后的原理之一。
阶梯式训练(Stagewise Training)是一种贪心算法,用于拟合加性模型。
步骤如下:
- 初始化模型 H 0 H_0 H0为 0,即最开始的模型不包含任何分类器。
- 从 m = 1 m = 1 m=1迭代到 T T T:
- 计算第 m m m个假设 H m H_m Hm,即在前一个加性模型 H m − 1 H_{m-1} Hm−1的基础上添加一个新的弱分类器 h m h_m hm和对应的权重 α m \alpha_m αm。
H m = H m − 1 + α m h m H_m = H_{m-1} + \alpha_m h_m Hm=Hm−1+αmhm - 找到使得损失函数 L \mathcal{L} L最小的弱分类器 h m h_m hm和权重 α m \alpha_m αm。这里 L \mathcal{L} L是损失函数, N N N是样本数量, t ( i ) t^{(i)} t(i)是第 i i i个样本的真实标签。
( h m , α m ) ← arg min h ∈ H , α ∑ i = 1 N L ( H m − 1 ( x ( i ) ) + α h ( x ( i ) ) , t ( i ) ) (h_m, \alpha_m) \leftarrow \arg\min_{h \in \mathcal{H}, \alpha} \sum_{i=1}^{N} \mathcal{L} \left( H_{m-1}(\mathbf{x}^{(i)}) + \alpha h(\mathbf{x}^{(i)}), t^{(i)} \right) (hm,αm)←argminh∈H,α∑i=1NL(Hm−1(x(i))+αh(x(i)),t(i)) - 将将找到的弱分类器 h m h_m hm及其权重 α m \alpha_m αm添加到加性模型中,更新模型为 H m = H m − 1 + α m h m H_m = H_{m-1} + \alpha_m h_m Hm=Hm−1+αmhm。
2.1.6.1 指数损失函数
指数损失函数定义为 L E ( z , t ) = exp ( − t z ) \mathcal{L}_E(z, t) = \exp(-tz) LE(z,t)=exp(−tz),其中 z z z是模型预测值, t t t是真实标签。
下图展示了不同损失函数随预测值 z z z的变化曲线:
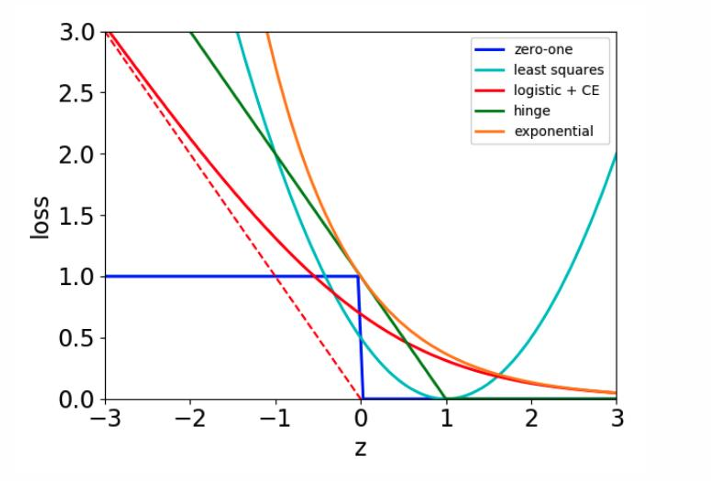
zero-one(蓝色实线):0-1损失,常用于分类问题。
least squares(青色实线):最小二乘损失,常用于回归问题。
logistic + CE(红色虚线):逻辑回归损失加交叉熵损失,常用于二分类问题。
hinge(绿色实线):合页损失,AdaBoost中常用的损失函数。
exponential(橙色实线):指数损失,强调了对错误预测的惩罚随着预测错误的增大而指数增长。
所以指数损失函数在预测值与真实标签相差较大时,损失增长速度更快,这使得模型在训练时更加关注那些难以分类的样本。
我们现在详细看一下加性模型的分阶段训练是如何进行的。
指数损失函数定义为 L E ( z , t ) = exp ( − t z ) \mathcal{L}_E(z, t) = \exp(-tz) LE(z,t)=exp(−tz),其中 z z z是模型预测值, t t t是真实标签。
找到使得指数损失函数最小化的弱分类器 h m h_m hm和权重 α m α_m αm。
( h m , α m ) ← arg min h ∈ H , α ∑ i = 1 N exp ( − [ H m − 1 ( x ( i ) ) + α h ( x ( i ) ) ] t ( i ) ) (h_m, \alpha_m) \leftarrow \arg\min_{h \in \mathcal{H}, \alpha} \sum_{i=1}^{N} \exp \left( - \left[ H_{m-1}(\mathbf{x}^{(i)}) + \alpha h(\mathbf{x}^{(i)}) \right] t^{(i)} \right) (hm,αm)←argminh∈H,α∑i=1Nexp(−[Hm−1(x(i))+αh(x(i))]t(i))
将损失函数展开为两部分的乘积。
= ∑ i = 1 N exp ( − H m − 1 ( x ( i ) ) t ( i ) ) exp ( − α h ( x ( i ) ) t ( i ) ) = \sum_{i=1}^{N} \exp \left( -H_{m-1}(\mathbf{x}^{(i)}) t^{(i)} \right) \exp \left( -\alpha h(\mathbf{x}^{(i)}) t^{(i)} \right) =∑i=1Nexp(−Hm−1(x(i))t(i))exp(−αh(x(i))t(i))
进一步简化为样本权重 w i ( m ) w_i^{(m)} wi(m)与指数项的乘积。
= ∑ i = 1 N w i ( m ) exp ( − α h ( x ( i ) ) t ( i ) ) = \sum_{i=1}^{N} w_i^{(m)} \exp \left( -\alpha h(\mathbf{x}^{(i)}) t^{(i)} \right) =∑i=1Nwi(m)exp(−αh(x(i))t(i))
这里我们定义 w i ( m ) ≜ exp ( − H m − 1 ( x ( i ) ) t ( i ) ) w_i^{(m)} \triangleq \exp \left( -H_{m-1}(\mathbf{x}^{(i)}) t^{(i)} \right) wi(m)≜exp(−Hm−1(x(i))t(i))不依赖于 h , α h, \alpha h,α。
我们想要解决以下最小化问题: ( h m , α m ) ← arg min h ∈ H , α ∑ i = 1 N w i ( m ) exp ( − α h ( x ( i ) ) t ( n ) ) (h_m, \alpha_m) \leftarrow \arg\min_{h \in \mathcal{H}, \alpha} \sum_{i=1}^{N} w_i^{(m)} \exp \left( -\alpha h(\mathbf{x}^{(i)}) t^{(n)} \right) (hm,αm)←argminh∈H,α∑i=1Nwi(m)exp(−αh(x(i))t(n))
这里, ( h m , α m ) (h_m, \alpha_m) (hm,αm)是第 m m m个弱分类器和对应的权重, H \mathcal{H} H是弱分类器的集合, w i ( m ) w_i^{(m)} wi(m)是第 m m m 轮迭代中第 i i i个样本的权重, α \alpha α是权重参数, h ( x ( i ) ) h(\mathbf{x}^{(i)}) h(x(i))是弱分类器对第 i i i个样本的预测, t ( n ) t^{(n)} t(n)是第 i i i个样本的真实标签。
前面我们推导过样本权重和指数损失的关系:
w ( n ) exp ( − α t h t ( x ( n ) ) t ( n ) ) ∝ w ( n ) exp ( 2 α t I { h t ( x ( n ) ) ≠ t ( n ) ) w^{(n)} \exp \left( -\alpha_t h_t(\mathbf{x}^{(n)}) t^{(n)} \right) \propto w^{(n)} \exp \left( 2\alpha_t \mathbb{I}\{h_t(\mathbf{x}^{(n)}) \neq t^{(n)} \right) w(n)exp(−αtht(x(n))t(n))∝w(n)exp(2αtI{ht(x(n))=t(n))
因此,对于 h m h_m hm,上述最小化等价于:
h m ← arg min h ∈ H ∑ i = 1 N w i ( m ) exp ( 2 α t I { h t ( x ( n ) ) ≠ t ( n ) ) h_m \leftarrow \arg\min_{h \in \mathcal{H}} \sum_{i=1}^{N} w_i^{(m)} \exp \left( 2\alpha_t \mathbb{I}\{h_t(\mathbf{x}^{(n)}) \neq t^{(n)} \right) hm←argminh∈H∑i=1Nwi(m)exp(2αtI{ht(x(n))=t(n))
进一步简化为:
= arg min h ∈ H ∑ i = 1 N w i ( m ) ( exp ( 2 α t I { h t ( x ( n ) ) ≠ t ( n ) ) − 1 ) = \arg\min_{h \in \mathcal{H}} \sum_{i=1}^{N} w_i^{(m)} \left( \exp \left( 2\alpha_t \mathbb{I}\{h_t(\mathbf{x}^{(n)}) \neq t^{(n)} \right) - 1 \right) \quad =argminh∈H∑i=1Nwi(m)(exp(2αtI{ht(x(n))=t(n))−1)
通过除以 exp ( 2 α t ) − 1 \exp(2\alpha_t) - 1 exp(2αt)−1 得到:
= arg min h ∈ H ∑ i = 1 N w i ( m ) I { h t ( x ( n ) ) ≠ t ( n ) } = \arg\min_{h \in \mathcal{H}} \sum_{i=1}^{N} w_i^{(m)} \mathbb{I}\{h_t(\mathbf{x}^{(n)}) \neq t^{(n)} \} =argminh∈H∑i=1Nwi(m)I{ht(x(n))=t(n)}
这意味着 h m h_m hm是加权 0/1 损失的最小化器。
现在我们已经获得了第 m m m个弱分类器 h m h_m hm,我们可以将其代入我们的指数损失目标函数并求解 a m a_m am。
推导结果为 α m = 1 2 log ( 1 − err m err m ) \alpha_m = \frac{1}{2} \log \left( \frac{1 - \text{err}_m}{\text{err}_m} \right) αm=21log(errm1−errm)
其中 err m \text{err}m errm是加权分类错误率:
err m = ∑ i = 1 N w i ( m ) I { h m ( x ( i ) ) ≠ t ( i ) } ∑ i = 1 N w i ( m ) \text{err}m = \frac{\sum{i=1}^{N} w_i^{(m)} \mathbb{I}\{h_m(\mathbf{x}^{(i)}) \neq t^{(i)}\}}{\sum{i=1}^{N} w_i^{(m)}} errm=∑i=1Nwi(m)∑i=1Nwi(m)I{hm(x(i))=t(i)}
这是指在第 m m m轮迭代中,弱分类器 h m h_m hm错误分类的样本的权重之和除以所有样本权重之和。
我们现在可以找到下一轮迭代的更新后的样本权重:
w i ( m + 1 ) = exp ( − H m ( x ( i ) ) t ( i ) ) w_i^{(m+1)} = \exp \left( -H_m(\mathbf{x}^{(i)}) t^{(i)} \right) wi(m+1)=exp(−Hm(x(i))t(i))
更新后的权重 w i ( m + 1 ) w_i^{(m+1)} wi(m+1)由当前模型 H m H_m Hm对第 i i i个样本的预测值和真实标签 t ( i ) t^{(i)} t(i)计算得出。
= exp ( − [ H m − 1 ( x ( i ) ) + α m h m ( x ( i ) ) ] t ( i ) ) = \exp \left( - \left[ H_{m-1}(\mathbf{x}^{(i)}) + \alpha_m h_m(\mathbf{x}^{(i)}) \right] t^{(i)} \right) =exp(−[Hm−1(x(i))+αmhm(x(i))]t(i))
这里 H m − 1 ( x ( i ) ) H_{m-1}(\mathbf{x}^{(i)}) Hm−1(x(i))是前一轮迭代的加性模型预测值, α m \alpha_m αm是第 m m m个弱分类器的权重, h m ( x ( i ) ) h_m(\mathbf{x}^{(i)}) hm(x(i))是第 m m m个弱分类器对第 i i i个样本的预测值。
= exp ( − H m − 1 ( x ( i ) ) t ( i ) ) exp ( − α m h m ( x ( i ) ) t ( i ) ) = \exp \left( -H_{m-1}(\mathbf{x}^{(i)}) t^{(i)} \right) \exp \left( -\alpha_m h_m(\mathbf{x}^{(i)}) t^{(i)} \right) =exp(−Hm−1(x(i))t(i))exp(−αmhm(x(i))t(i))
将上式展开,得到前一轮模型预测和当前弱分类器预测的乘积。
= w i ( m ) exp ( − α m h m ( x ( i ) ) t ( i ) ) = w_i^{(m)} \exp \left( -\alpha_m h_m(\mathbf{x}^{(i)}) t^{(i)} \right) =wi(m)exp(−αmhm(x(i))t(i))
最终表达式显示,更新后的权重是当前权重 w i ( m ) w_i^{(m)} wi(m)乘以 exp ( − α m h m ( x ( i ) ) t ( i ) ) \exp \left( -\alpha_m h_m(\mathbf{x}^{(i)}) t^{(i)} \right) exp(−αmhm(x(i))t(i)),这反映了当前弱分类器对每个样本预测的影响。
2.1.7 AdaBoost 算法小结
总结起来,我们得到了加性模型 H m ( x ) = ∑ i = 1 m α i h i ( x ) H_m(\mathbf{x}) = \sum_{i=1}^{m} \alpha_i h_i(\mathbf{x}) Hm(x)=∑i=1mαihi(x),其中:
h m ← arg min h ∈ H ∑ i = 1 N w i ( m ) I { h ( x ( i ) ) ≠ t ( i ) } h_m \leftarrow \arg\min_{h \in \mathcal{H}} \sum_{i=1}^{N} w_i^{(m)} \mathbb{I}\{h(\mathbf{x}^{(i)}) \neq t^{(i)}\} hm←argminh∈H∑i=1Nwi(m)I{h(x(i))=t(i)}
找到使得加权错误率最小的弱分类器 h m h_m hm。
α = 1 2 log ( 1 − err m err m ) \alpha = \frac{1}{2} \log \left( \frac{1 - \text{err}_m}{\text{err}_m} \right) α=21log(errm1−errm)
计算第 m m m个弱分类器的权重 α α α,其中 err m \text{err}m errm是第 m m m个弱分类器的错误率。
err m = ∑ i = 1 N w i ( m ) I { h m ( x ( i ) ) ≠ t ( i ) } ∑ i = 1 N w i ( m ) \text{err}m = \frac{\sum{i=1}^{N} w_i^{(m)} \mathbb{I}\{h_m(\mathbf{x}^{(i)}) \neq t^{(i)}\}}{\sum{i=1}^{N} w_i^{(m)}} errm=∑i=1Nwi(m)∑i=1Nwi(m)I{hm(x(i))=t(i)}
计算第 m m m个弱分类器的加权错误率 err m \text{err}_m errm。
w i ( m + 1 ) = w i ( m ) exp ( − α m h m ( x ( i ) ) t ( i ) ) w_i^{(m+1)} = w_i^{(m)} \exp \left( -\alpha_m h_m(\mathbf{x}^{(i)}) t^{(i)} \right) wi(m+1)=wi(m)exp(−αmhm(x(i))t(i))
更新第 i i i个样本在第 m + 1 m+1 m+1轮迭代中的权重 w i ( m + 1 ) w_i^{(m+1)} wi(m+1)
2.2 小结
Boosting通过生成一系列弱分类器的集成来减少偏差。
这里的"弱分类器"指的是性能略优于随机猜测的分类器,它们是算法中的基本构建块。
每个分类器都被训练来减少前一个集成的错误。
它对过拟合相当有抵抗力,尽管它也可能过拟合。
3. 集成学习
我们今天学习了集成学习的两种主要方法:Boosting(提升法)和 Bagging(装袋法)。
集成方法通过组合多个分类器来提高性能。
Boosting(提升法):
- 提升法通过逐步纠正前一个模型的错误来减少模型的偏差。
- 由于模型是顺序训练的,集成的方差增加,可能导致过拟合。
- 模型是顺序训练的,每个模型依赖于前一个模型的结果。
- 集成中的元素之间存在高度依赖性。
Bagging(装袋法):
- 装袋法通过并行训练多个模型来减少方差,大的集成不会引发过拟合。
- 装袋法对模型的偏差影响不大。
- 模型可以并行训练,因为它们是独立于彼此的。
- 目标是最小化集成元素之间的相关性,以进一步减少方差。
因此我们可以得到。
| 方法 | 主要目标 | 偏差(Bias) | 方差(Variance) | 风险 |
|---|---|---|---|---|
| Bagging | 降低方差 | 几乎不变 | ✅ 显著降低 | 欠拟合风险小 |
| Boosting | 降低偏差 | ✅ 显著降低 | 可能略升 | 过拟合风险大 |