1 引言
在现代信号处理领域,非平稳信号广泛存在于通信、机械振动、生物医学及地球物理等场景中,其频率成分随时间动态变化,传统傅里叶变换因仅能提供整体频谱信息而难以揭示信号的时变特性。时频分析 (Joint Time-Frequency Analysis, JTFA)作为一种同时刻画信号时域与频域联合特性的技术,通过构建时频分布函数,能够直观呈现信号能量在时间-频率平面上的演化规律,成为解析非平稳信号特征的核心工具。
时频分析的核心思想在于突破单一域分析的局限性,例如短时傅里叶变换(STFT)通过滑动窗函数实现局部频谱估计,但其固定的时频分辨率受限于测不准原理,难以兼顾瞬态与稳态信号分析;而小波变换通过多尺度分解提供自适应分辨率,但缺乏直接的相位信息。针对这些问题,Wigner-Ville分布(WVD)等双线性时频表示方法通过提升能量聚集性显著改善时频分辨率,但其固有的交叉项干扰问题促使研究者提出平滑伪WVD(SPWVD)等改进方案。此外,希尔伯特-黄变换(HHT)通过经验模态分解(EMD)与瞬时频率计算,为非线性信号分析提供了新范式。
2时频分析算法

2.1 短时傅里叶变换
2.1.1 STFT基本原理
短时傅里叶变换通过滑动窗口截取信号片段,对每个片段进行傅里叶变换,构建时频分布矩阵。其核心公式为:

分辨率权衡:
时间分辨率:由窗长决定,窗长越短,时间分辨率越高,但频率分辨率越低。
频率分辨率:由FFT点数(nfft)决定,nfft越大,频率分辨率越高,但计算量增加。
matlab
%%
% 短时傅里叶变换时频分析
%%
% 生成测试信号(含两个频率分量)
fs = 1000;
t = 0:1/fs:1-1/fs;
x = sin(2*pi*50*t) + 0.5*sin(2*pi*150*t);
% 参数设置
wlen = 256; % 窗长
hop = 128; % 重叠(50%)
nfft = 512; % FFT点数
win = hamming(wlen); % 窗函数
% 计算STFT
[S, F, T] = spectrogram(x, win, hop, nfft, fs);
% 可视化时频图(dB尺度)
figure('name' , '短时傅里叶变换');
subplot(2 ,1,1);
plot(x);
title('原始信号');
subplot(2 ,1,2);
imagesc(T, F, 20*log10(abs(S)));
axis xy;
colormap(jet);
xlabel('时间 (s)');
ylabel('频率 (Hz)');
title('STFT时频图(dB)');
colorbar;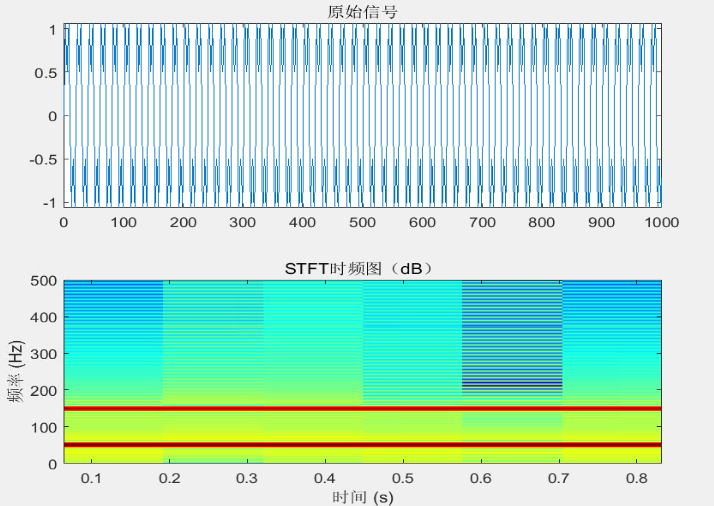
2.1.2关键参数影响分析
1. 窗长(wlen)
时间分辨率:窗长越短,时间分辨率越高(适合快速变化的信号)。
频率分辨率:窗长越长,频率分辨率越高(适合稳定频率成分)。
matlab
figure('name' , '短时傅里叶变换:不同窗长');
% 窗长256(左) vs 1024(右)
subplot(2,1,1);
spectrogram(x, hamming(256), 128, 512, fs);
title('窗长256');
subplot(2,1,2);
spectrogram(x, hamming(512), 256, 512, fs);
title('窗长512');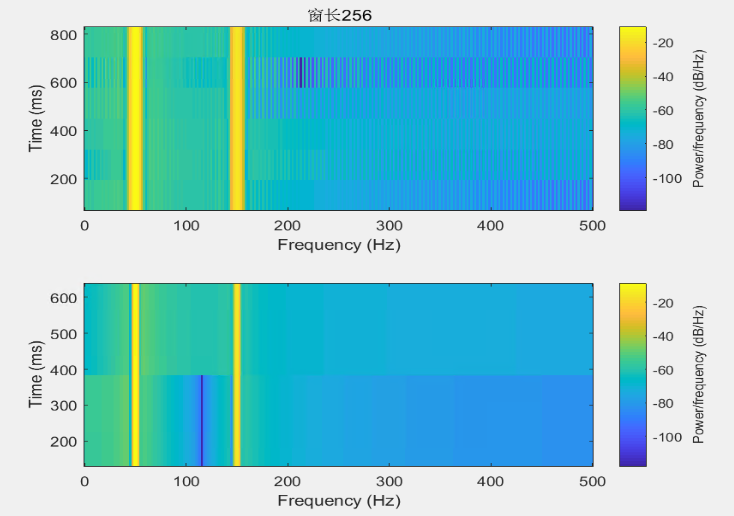
2. 重叠步长(noverlap)
时间平滑:重叠比例越高(如75%),时频图时间轴更平滑,但计算量增加。
频谱泄漏抑制:适当重叠可减少频谱泄漏。
3. FFT点数(nfft)
频率刻度精度:nfft越大,频率轴分辨率越高(如nfft=2048可分辨1Hz间隔)。
频谱泄漏:增大nfft可降低频谱泄漏,但需权衡计算效率。
2.2 提取时频脊
提取时频脊(Instantaneous Frequency),跟踪信号频率随时间的变化
matlab
%%
% 提取时频脊线进行时频分析
%%
close all;
% 生成线性调频信号(0Hz→250Hz)
fs = 1000;
t = 0:1/fs:1-1/fs;
x1 = chirp(t, 0, 1, 250);%0~250HZ线性调频
%双频
is_two_signal = 0;
if is_two_signal == 0
x2 = 0.3*randn(size(t)); % 噪声
else
x2 = chirp(t, 200, 1, 300) + 0.3*randn(size(t)); % 200Hz→300Hz
end
x = x1 + x2;
% 计算短时傅里叶变换(STFT)
% 参数设置
wlen = 256; hop = 250; nfft = 512;
win = hamming(wlen); % 窗函数选择
% 计算STFT
%添加汉明窗
[stft, f, t_stft] = spectrogram(x, win, hop, nfft, fs);
%[stft, f, t_stft] = spectrogram(x, 256, 250, 512, fs);
% 提取时频脊线
penalty = 0.1; % 低惩罚允许频率跳变,值越大脊线越平滑
if is_two_signal == 0
[fridge, iridge] = tfridge(stft, f, penalty, 'NumRidges', 1);
else
[fridge, iridge] = tfridge(stft, f, penalty, 'NumRidges', 2);
end
% 可视化
figure('name', '线性调频信号时频分析');
subplot(3,1,1);
plot(x);
title('原始信号');
subplot(3,1,2);
imagesc(t_stft, f, 20*log10(abs(stft))); axis xy;
colormap(jet); colorbar;
xlabel('时间 (s)'); ylabel('频率 (Hz)');
title('STFT时频图');
subplot(3,1,3);
hold on;
plot(t_stft, fridge, 'LineWidth', 2);
xlabel('时间 (s)');
ylabel('频率 (Hz)');
legend('脊线');
title('瞬时频率提取结果');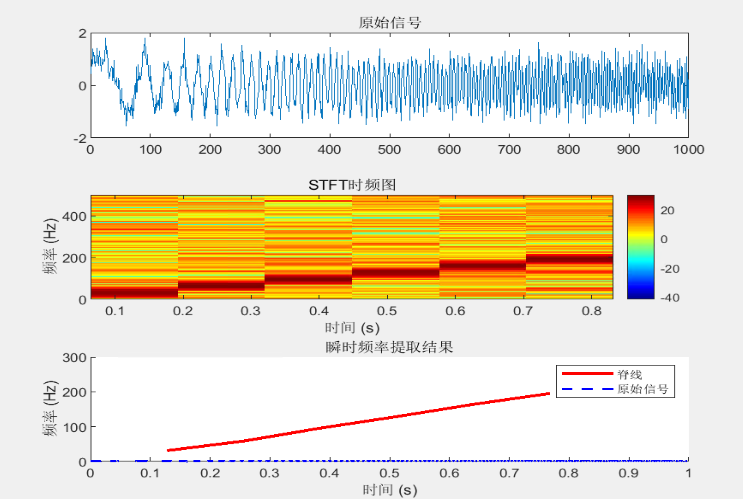
2.3 WVD时频分析
计算Wigner-Ville分布(WVD),显示信号的时频能量分布
matlab
%单分量正弦信号的WVD分析
% 参数设置
fs = 1000; % 采样频率
t = 0:1/fs:1-1/fs; % 时间向量(1秒)
f = 50; % 信号频率
x = sin(2*pi*f*t) + 0.3*randn(size(t)); % 正弦信号
figure('name' ,'原始信号');
subplot(3,1,1)
plot(x);
title('原始信号');
%傅里叶变换
Y = fft(x);
L = length(x);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = fs*(0:(L/2))/L;
subplot(3,1,2);
plot(f,P1)
title('Single-Sided Amplitude Spectrum of X(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')
% 计算WVD
[wvd_matrix, t_axis, f_axis] = wvd(x, fs);
subplot(3,1,3);
% 绘制时频图
imagesc(t_axis./(fs/2), f_axis.*(fs/2), abs(wvd_matrix));
axis xy;
colormap(jet);
colorbar;
xlabel('时间 (s)');
ylabel('频率 (Hz)');
title('单分量正弦信号的WVD时频图');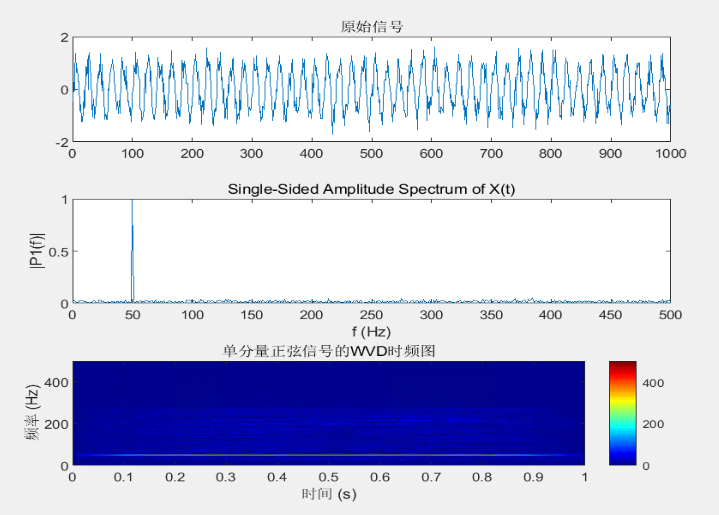
2.4 hht 希尔伯特-黄变换
希尔伯特-黄变换(HHT),包括经验模态分解(EMD)和希尔伯特谱
matlab
%%
% 希尔伯特-黄变换(HHT)的完整示例
%%
close all;
% 参数设置
load('sinusoidalSignalExampleData.mat','X','fs');
t = (0:length(X)-1)/fs;
% 执行EMD分解
[imf,residual,info] = emd(X,'Interpolation','pchip');
len = size(imf ,2);
figure('name' ,'emd分解');
subplot(len+1,1,1);
plot(t,X);
xlabel('Time(s)');
title('原始信号');
for i = 2:len+1
subplot(len+1,1,i);
plot(imf(:,i-1));
str = sprintf('第%d个imf分类' ,i-1);
title(str);
end
%Hilbert变换与时频分析
% 计算Hilbert谱
figure('name' ,'hht分析');
subplot(2,1,1);
hht(imf, fs);
title('hht默认时频图');
[hs, f, t] = hht(imf, fs);
hs_log = log10(hs); % 对数变换
hs_norm = hs_log / max(hs_log(:)); % 归一化到0~1
% 绘制一致的时频图
subplot(2,1,2);
imagesc(t, f, hs_log);
colormap(jet);
colorbar; % 设置颜色条范围与默认一致
xlabel('时间 (s)');
ylabel('频率 (Hz)');
title('Hilbert时频谱');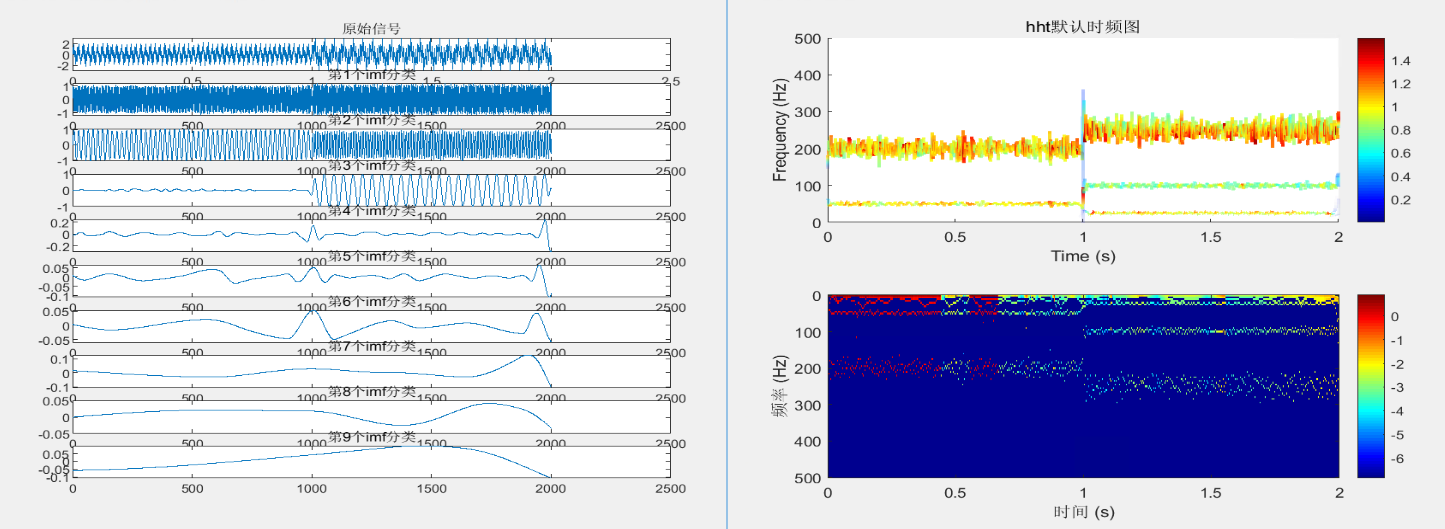
2.5 pspectrum 综合时频分析
pspectrum
综合时频分析函数,支持STFT、CWT等多种变换,输出时频功率谱
matlab
%%
% pspectrum功率谱分析
%%
close all;
% 生成测试信号(含200Hz和500Hz正弦波)
fs = 1000; t = 0:1/fs:1-1/fs;
x = sin(2*pi*200*t) + 0.5*sin(2*pi*500*t) + 0.2*randn(size(t));
% 计算功率谱
p = pspectrum(x, fs, 'Leakage', 0.85);
% 绘制频谱图(dB尺度)
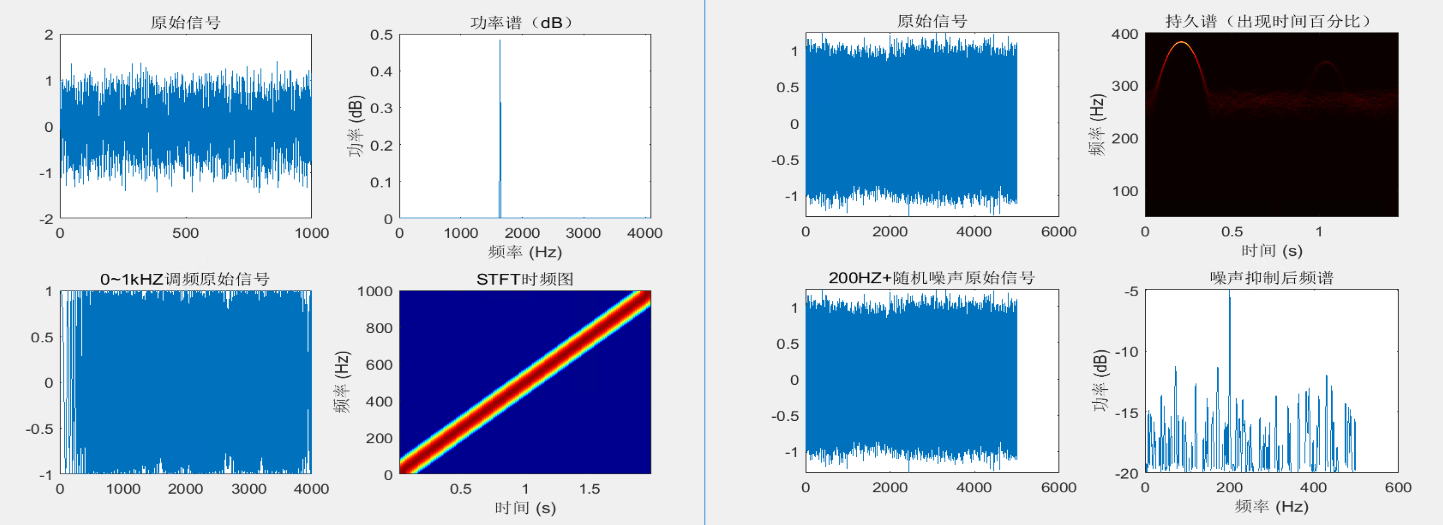
figure('name' ,'功率谱分析');
subplot(2,2,1);
plot(x);
title('原始信号');
subplot(2,2,2);
plot(p);
title('功率谱(dB)');
xlabel('频率 (Hz)');
ylabel('功率 (dB)');
% 生成调频信号(0Hz→1kHz)
fs = 2000; t = 0:1/fs:2-1/fs;
x = chirp(t, 0, 2, 1000);
% 计算时频谱
[p, f, t_stft] = pspectrum(x, fs, 'spectrogram', ...
'TimeResolution', 0.05, 'OverlapPercent', 75, 'MinThreshold', -40);
% 可视化时频图
subplot(2,2,3);
plot(x);
title('0~1kHZ调频原始信号');
subplot(2,2,4);
imagesc(t_stft, f, 10*log10(p));
axis xy;
colormap(jet);
xlabel('时间 (s)');
ylabel('频率 (Hz)');
title('STFT时频图');
% 生成含间歇干扰的信号
fs = 1000; t = 0:1/fs:5-1/fs;
carrier = sin(2*pi*100*t);
interference = 0.3*sin(2*pi*300*t).*(t>1 & t<2);
x = carrier + interference + 0.1*randn(size(t));
% 计算持久谱
[p, f, t_persist] = pspectrum(x, fs, 'persistence', ...
'FrequencyLimits', [50, 400], 'TimeResolution', 0.1);
% 绘制持久谱(热力图)
figure('name' ,'热力图分析');
subplot(2,2,1);
plot(x);
title('原始信号');
subplot(2,2,2);
imagesc(t_persist, f, p);
axis xy;
colormap(hot);
xlabel('时间 (s)');
ylabel('频率 (Hz)');
title('持久谱(出现时间百分比)');
% 生成含强噪声的信号
fs = 1000; t = 0:1/fs:1-1/fs;
x_clean = sin(2*pi*200*t);
x_noisy = x_clean + 1.5*randn(size(t)); % SNR≈3dB
% 设置最小阈值过滤噪声
[p, f] = pspectrum(x_noisy, fs, 'MinThreshold', -20);
% 绘制带噪声抑制的频谱
subplot(2,2,3);
plot(x);
title('200HZ+随机噪声原始信号');
subplot(2,2,4);
plot(f, 10*log10(p));
title('噪声抑制后频谱');
xlabel('频率 (Hz)');
ylabel('功率 (dB)');