排序算法：归并排序算法

文章目录

- 一、归并排序算法简介
- 二、图示解析
- [三、时间 & 空间复杂度分析](#三、时间 & 空间复杂度分析)
- 四、归并排序完整示例代码

一、归并排序算法简介

归并排序（Merge Sort）是一种典型的分治（Divide & Conquer）排序算法。一句话总结：先拆分到最小，再两两合并成有序序列

核心特点：

稳定排序

特别适合大数据 / 外排序 / 链表

归并排序的核心思想

归并排序分三步：

分（Divide）：把数组递归地一分为二

治（Conquer）：对子数组排序

合（Merge）：将两个有序数组合并成一个有序数组

二、图示解析

假设数组：

cpp 复制代码

[8, 3, 1, 7, 0, 10, 2]

分裂阶段（递归拆分）

cpp 复制代码

                [8, 3, 1, 7, 0, 10, 2]
                         |
              --------------------------------
              |                              |
        [8, 3, 1]                     [7, 0, 10, 2]
           |                                  |
      -----------                      -----------------
      |         |                      |               |
    [8]      [3,1]                  [7,0]           [10,2]
               |                      |                 |
            [3] [1]                [7] [0]           [10] [2]

合并阶段（关键步骤）

合并 $3$ 和 $1$

cpp 复制代码

[1, 3]

合并 $8$ 和 $1, 3$

cpp 复制代码

[1, 3, 8]

合并 $7$ 和 $0$

cpp 复制代码

[0, 7]

合并 $10$ 和 $2$

cpp 复制代码

[2, 10]

合并 $0,7$ 和 $2,10$

cpp 复制代码

[0, 2, 7, 10]

最终合并

cpp 复制代码

[1, 3, 8] + [0, 2, 7, 10]
        ↓
[0, 1, 2, 3, 7, 8, 10]

三、时间 & 空间复杂度分析

时间复杂度（非常稳定）

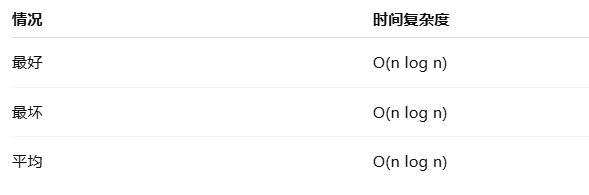
空间复杂度：O(n)（需要辅助数组）

四、归并排序完整示例代码

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

/* ---------------- 合并两个有序区间 ---------------- */
void merge(vector<int>& arr, int left, int mid, int right)
{
    vector<int> temp;
    int i = left;
    int j = mid + 1;

    while (i <= mid && j <= right)
    {
        if (arr[i] <= arr[j])
            temp.push_back(arr[i++]);
        else
            temp.push_back(arr[j++]);
    }

    while (i <= mid) temp.push_back(arr[i++]);
    while (j <= right) temp.push_back(arr[j++]);

    for (int k = 0; k < temp.size(); k++)
        arr[left + k] = temp[k];
}

/* ---------------- 归并排序 ---------------- */
void mergeSort(vector<int>& arr, int left, int right)
{
    if (left >= right) return;

    int mid = (left + right) / 2;

    mergeSort(arr, left, mid);
    mergeSort(arr, mid + 1, right);
    merge(arr, left, mid, right);
}

int main()
{
    vector<int> arr = {8, 3, 1, 7, 0, 10, 2};

    mergeSort(arr, 0, arr.size() - 1);

    for (int x : arr)
        cout << x << " ";
}