数据结构和算法：Morris遍历

WBluuue2025-12-24 14:33

前言

这个感觉竞赛里也用不到，随便学学吧（）

一、原理

1.内容

（1）核心

没有左子树的节点只到达一次，有左子树的节点会到达两次，其中用左子树最右节点的右指针状态来标记第几次到达。

（2）过程

首先，开始时cur在头节点，cur为空时整个过程停止。

若cur没有左孩子，就向右移动。

若cur有左孩子，就去找cur左子树的最右节点mostRight。若mostRight的右指针为空，那么就让其指向cur，然后cur向左移动。若mostRight右指针指向cur，就让其指向空，然后cur向右移动。

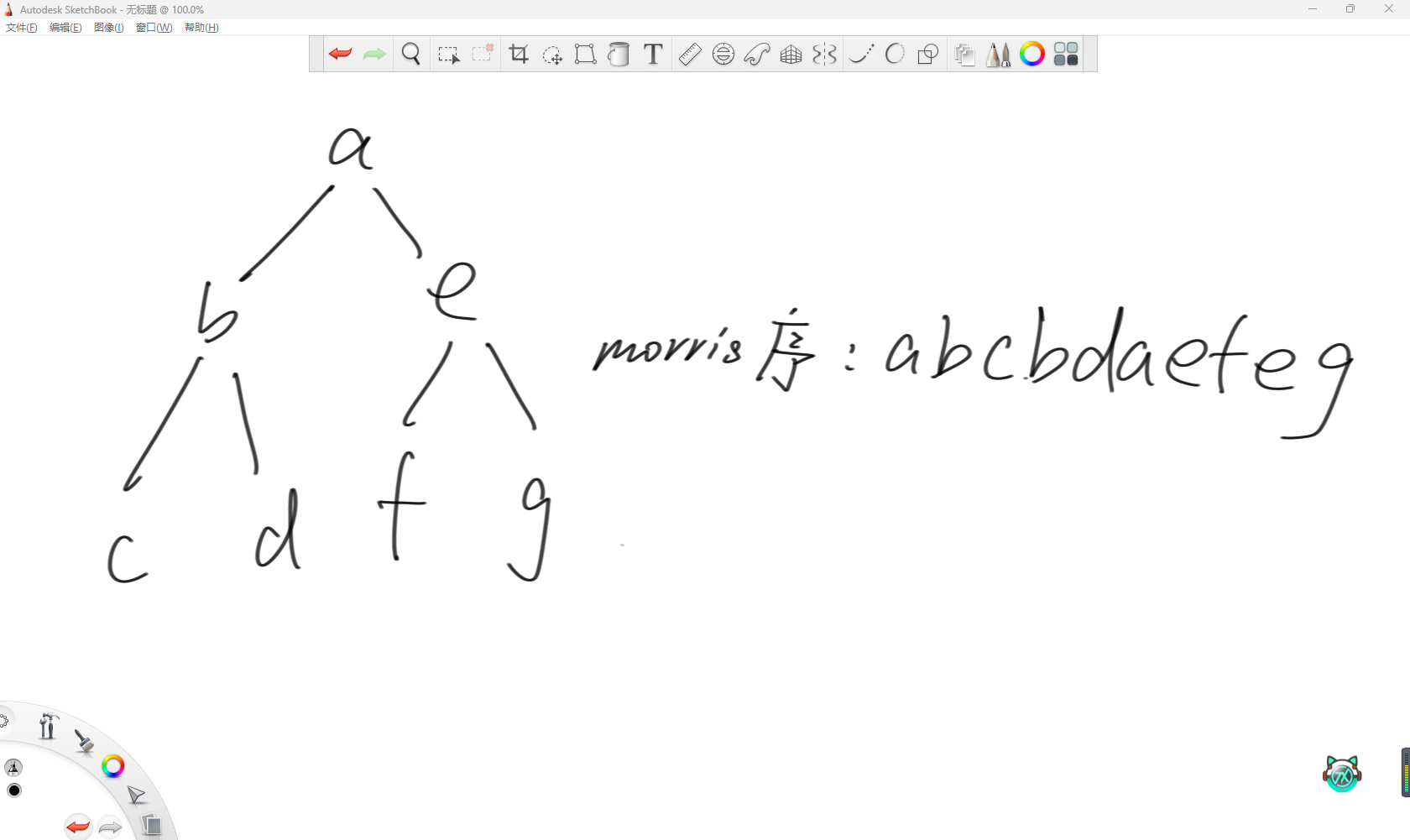
首先cur肯定先来到a节点。之后，因为a节点有左孩子，那么就去a节点左子树的最右节点，所以就是d节点。因为此时d节点的右指针为空，所以让其指向a节点，然后cur来到b节点。

之后，因为b节点有左孩子，所以还是去找左子树的最右节点，那么就是c节点。同样因为此时c节点右指针为空，所以让其指向b节点，然后cur来到c节点。

当cur来到c节点时，因为没有左孩子，那么就向右移动，所以cur回到b节点。此时再去找左子树的最右节点，可以发现c节点的右指针指向自己，所以c节点的右指针指向空，然后cur往右去d节点。

之后因为没有左孩子，所以往右回到a节点，同样去找左子树的最右节点，发现d节点的右指针指回来了，所以将其指为空，cur往右来到e节点。

之后就是把f节点的右指针指向e，然后来到f，之后回到e，把f的右指针指回空，然后去g，完成遍历。观察整个过程，不难发现时间复杂度就是O(n)的，空间复杂度O(1)。

2.二叉树的前序遍历

cpp 复制代码 
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {

        vector<int>ans;

        return morrisPreorder(root,ans);
    }

    vector<int>morrisPreorder(TreeNode* head,vector<int>&ans)
    {
        TreeNode* cur=head;
        TreeNode* mostRight=NULL;
        
        while(cur!=NULL)
        {
            mostRight=cur->left;

            //cur有左树
            if(mostRight!=NULL)
            {
                while(mostRight->right!=NULL&&mostRight->right!=cur)
                {
                    mostRight=mostRight->right;
                }

                //最右节点右指针为空 -> 第一次到达
                if(mostRight->right==NULL)
                {
                    ans.push_back(cur->val);

                    mostRight->right=cur;
                    cur=cur->left;
                    continue;
                }
                //右指针为cur -> 第二次到达
                else
                {
                    mostRight->right=NULL;
                } 
            }
            //没左树 -> 直接收集
            else
            {
                ans.push_back(cur->val);
            }

            cur=cur->right;
        }

        return ans;
    }

    //Morris遍历模板
    void morris(TreeNode* head)
    {
        TreeNode* cur=head;
        TreeNode* mostRight=NULL;
        
        while(cur!=NULL)
        {
            mostRight=cur->left;

            //cur有左树
            if(mostRight!=NULL)
            {
                while(mostRight->right!=NULL&&mostRight->right!=cur)
                {
                    mostRight=mostRight->right;
                }

                //最右节点右指针为空
                if(mostRight->right==NULL)
                {
                    mostRight->right=cur;
                    cur=cur->left;
                    continue;
                }
                //右指针为cur
                else
                {
                    mostRight->right=NULL;
                } 
            }

            cur=cur->right;
        }
    }
};

先序遍历就是在morris遍历的过程中，只在第一次来到时打印该节点，第二次来到时不打印。而观察morris遍历的特点，当最右节点的右指针是cur，那么就说明此时是第二次来到这个节点，所以就不打印。

3.二叉树的中序遍历

cpp 复制代码 
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        
        vector<int>ans;

        return morrisInorder(root,ans);
    }

    vector<int>morrisInorder(TreeNode* head,vector<int>&ans)
    {
        TreeNode* cur=head;
        TreeNode* mostRight=NULL;
        
        while(cur!=NULL)
        {
            mostRight=cur->left;

            //cur有左树
            if(mostRight!=NULL)
            {
                while(mostRight->right!=NULL&&mostRight->right!=cur)
                {
                    mostRight=mostRight->right;
                }

                //最右节点右指针为空 -> 第一次到达
                if(mostRight->right==NULL)
                {
                    mostRight->right=cur;
                    cur=cur->left;
                    continue;
                }
                //右指针为cur -> 第二次到达
                else
                {
                    ans.push_back(cur->val);

                    mostRight->right=NULL;
                } 
            }
            //没左树 -> 直接收集
            else
            {
                ans.push_back(cur->val);
            }

            cur=cur->right;
        }

        return ans;
    }
};

中序遍历就是在morris遍历的过程中，若只来一次，那么就直接打印，否则就在第二次来的时候再打印。根据morris遍历，有左子树的节点会来两遍，所以如果没有就直接打印，有的话就在最右节点右指针指向自己时输出。

4.二叉树的后序遍历

cpp 复制代码 
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        
        vector<int>ans;

        return morrisPostorder(root,ans);
    }

    vector<int> morrisPostorder(TreeNode* head,vector<int>&ans)
    {
        TreeNode* cur=head;
        TreeNode* mostRight=NULL;
        
        while(cur!=NULL)
        {
            mostRight=cur->left;

            //cur有左树
            if(mostRight!=NULL)
            {
                while(mostRight->right!=NULL&&mostRight->right!=cur)
                {
                    mostRight=mostRight->right;
                }

                //最右节点右指针为空
                if(mostRight->right==NULL)
                {
                    mostRight->right=cur;
                    cur=cur->left;
                    continue;
                }
                //右指针为cur -> 第二次到达
                else
                {
                    mostRight->right=NULL;

                    collect(cur->left,ans);
                } 
            }

            cur=cur->right;
        }

        collect(head,ans);

        return ans;
    }

    void collect(TreeNode* head,vector<int>&ans)
    {
        TreeNode* tail=reverse(head);
        TreeNode* cur=tail;
        while(cur!=NULL)
        {
            ans.push_back(cur->val);
            cur=cur->right;
        }
        reverse(tail);
    }

    //类似单链表的反转
    TreeNode* reverse(TreeNode* cur)
    {
        TreeNode* pre=NULL;
        TreeNode* next=NULL;

        while(cur!=NULL)
        {
            next=cur->right;
            cur->right=pre;
            pre=cur;
            cur=next;
        }

        return pre;
    }
};

后序遍历就是在morris遍历时，在第二次到达某个节点时，去逆序收集该节点左树的右边界，最后逆序收集整棵树的右边界。对于逆序操作，就类似于单链表的反转，记得最后需要反转回去。

5.Morris遍历的局限性

很容易就能看出，局限性就是每个节点来到的次数比较少。因为morris遍历每个点最多来两次，而dfs每个点会来三次，所以一些需要dfs整合信息的情况morris就不适用了.

二、应用

1.验证二叉搜索树

cpp 复制代码 
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        TreeNode* cur=root;
        TreeNode* mostRight=NULL;

        TreeNode* pre=NULL;
        bool ans=true;
        
        while(cur!=NULL)
        {
            mostRight=cur->left;

            //cur有左树
            if(mostRight!=NULL)
            {
                while(mostRight->right!=NULL&&mostRight->right!=cur)
                {
                    mostRight=mostRight->right;
                }

                //最右节点右指针为空
                if(mostRight->right==NULL)
                {
                    mostRight->right=cur;
                    cur=cur->left;
                    continue;
                }
                //右指针为cur
                else
                {
                    mostRight->right=NULL;
                } 
            }

            //中序遍历值单调递增就是BST
            //不能直接返回！要把树改回来！
            if(pre!=NULL&&pre->val>=cur->val)
            {
                ans=false;
            }

            pre=cur;
            cur=cur->right;
        }

        return ans;
    }
};

因为中序遍历时值单调递增就是BST，所以直接中序遍历即可。所以多用一个pre变量记录上一个位置，然后每次比较即可。注意这里不能直接返回，需要都把那么改过的右指针改回来，最后再返回。

2.二叉树的最小深度

太逆天了......

cpp 复制代码 
class Solution {
public:
    int minDepth(TreeNode* head) {
        
        if(head==NULL)
        {
            return 0;
        }

        TreeNode* cur=head;
        TreeNode* mostRight=NULL;
        
        //morris遍历中，上个节点所在的层数
        int preLevel=0;

        //树的右边界长度
        int rightLen=0;

        int ans=1e9;
        while(cur!=NULL)
        {
            mostRight=cur->left;

            //cur有左树
            if(mostRight!=NULL)
            {
                rightLen=1;
                while(mostRight->right!=NULL&&mostRight->right!=cur)
                {
                    rightLen++;
                    mostRight=mostRight->right;
                }

                //最右节点右指针为空 -> 第一次来
                if(mostRight->right==NULL)
                {
                    preLevel++;
                    mostRight->right=cur;
                    cur=cur->left;
                    continue;
                }
                //右指针为cur -> 第二次来
                else
                {
                    //是叶节点
                    if(mostRight->left==NULL)
                    {
                        ans=min(ans,preLevel);
                    }

                    //当前层数为左树最右节点层数减去左树右边界长度
                    preLevel-=rightLen;
                    mostRight->right=NULL;
                } 
            }
            //没有左树 -> 必然从上方来的
            else
            {
                preLevel++;
            }

            cur=cur->right;
        }

        //整棵树的最右节点
        rightLen=1;
        cur=head;
        while(cur->right!=NULL)
        {
            rightLen++;
            cur=cur->right;
        }

        //是叶节点
        if(cur->left==NULL)
        {
            ans=min(ans,rightLen);
        }

        return ans;
    }
};

考虑再多设置两个变量，preLevel表示上一个节点所在的层数，rightLen为树右边界的长度，所以在找最右节点时可以求得rightLen。之后，若是第一次来，因为之后cur要左移，所以preLevel直接加一。而如果是第二次来，那么如果此时的最右节点是叶节点，那么就可以直接统计ans了。否则，当前的层数就是左树最右节点的层数减去这个最右边界的长度。另外，如果压根没有左树，那么必然是从上方节点来的，所以preLevel直接加一即可。

注意，当遍历结束后，整棵树的最右节点是没有被统计过的，所以需要额外特判一下。

3.二叉树的最近公共祖先

cpp 复制代码 
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* head, TreeNode* o1, TreeNode* o2) {
        
        //特判是否其中一个是另一个的lca
        if(preOrder(o1->left,o1,o2)!=NULL||preOrder(o1->right,o1,o2)!=NULL)
        {
            return o1;
        }
        if(preOrder(o2->left,o1,o2)!=NULL||preOrder(o2->right,o1,o2)!=NULL)
        {
            return o2;
        }

        //先序遍历中，谁先被找到谁在左
        TreeNode* lleft=preOrder(head,o1,o2);
        
        TreeNode* cur=head;
        TreeNode* mostRight=NULL;
        TreeNode* ans=NULL;
        while(cur!=NULL)
        {
            mostRight=cur->left;

            //cur有左树
            if(mostRight!=NULL)
            {
                while(mostRight->right!=NULL&&mostRight->right!=cur)
                {
                    mostRight=mostRight->right;
                }

                //最右节点右指针为空
                if(mostRight->right==NULL)
                {
                    mostRight->right=cur;
                    cur=cur->left;
                    continue;
                }
                //右指针为cur
                else
                {
                    mostRight->right=NULL;

                    if(ans==NULL)
                    {
                        //lleft在左树右边界上
                        if(rightCheck(cur->left,lleft))
                        {
                            //看lleft的右树里是否有另一个
                            if(preOrder(lleft->right,o1,o2)!=NULL)
                            {
                                ans=lleft;
                            }
                            lleft=cur;
                        }
                    }
                } 
            }

            cur=cur->right;
        }

        //额外检查最后一个lleft

        return ans!=NULL?ans:lleft;
    }

    //以head为头的树进行先序遍历，o1和o2谁先被找到就返回谁
    TreeNode* preOrder(TreeNode* head,TreeNode* o1,TreeNode* o2)
    {
        TreeNode* cur=head;
        TreeNode* mostRight=NULL;
        TreeNode* ans=NULL;
        
        while(cur!=NULL)
        {
            mostRight=cur->left;

            //cur有左树
            if(mostRight!=NULL)
            {
                while(mostRight->right!=NULL&&mostRight->right!=cur)
                {
                    mostRight=mostRight->right;
                }

                //最右节点右指针为空 -> 第一次到达
                if(mostRight->right==NULL)
                {
                    if(ans==NULL&&(cur==o1||cur==o2))
                    {
                        ans=cur;
                    }

                    mostRight->right=cur;
                    cur=cur->left;
                    continue;
                }
                //右指针为cur -> 第二次到达
                else
                {
                    mostRight->right=NULL;
                } 
            }
            //没左树 -> 直接收集
            else
            {
                if(ans==NULL&&(cur==o1||cur==o2))
                {
                    ans=cur;
                }
            }

            cur=cur->right;
        }

        return ans;
    }

    bool rightCheck(TreeNode* head, TreeNode* target)
    {
        while(head!=NULL)
        {
            if(head==target)
            {
                return true;
            }
            head=head->right;
        }
        return false;
    }
};

感觉这个的思路和tarjan算法求lca很类似（？

首先，定义preOrder方法为从某个节点开始，o1和o2谁先被找到就返回谁，所以上来可以先特判两者是否其中一个是另一个的lca。之后，再从head开始preOrder一遍，那么此时谁先被找到谁就是左侧的节点left。

之后去跑morris遍历，当第二次来到当前节点时，去check看left是否在cur左树右边界上。如果在，那么就去看left的右树里是否有另一个。如果有，那么此时的left就是lca。否则就把left设置为当前节点cur。注意最后需要额外再考虑一下最后的left。

大体的原理就是因为已经找到left了，所以就只用查右树即可。

总结

了解一下就行了～

END

相关推荐
客梦4 小时前
数据结构-红黑树
数据结构·笔记
scx201310044 小时前
20251117Manacher总结
算法·manacher
qq_433554544 小时前
C++状压DP
开发语言·c++
(●—●)橘子……4 小时前
记力扣42.接雨水 练习理解
笔记·学习·算法·leetcode·职场和发展
夏幻灵4 小时前
ASCII 码的具体含义和作用
c++
Bin二叉4 小时前
南京大学cpp复习（c10——多态、操作符重载）
开发语言·c++·笔记·学习
旺仔小拳头..5 小时前
数据结构（三）----树/二叉树/完全二叉树/线索二叉树/哈夫曼树/树、二叉树、森林之间的转换/前 中 后序遍历
算法
Sheep Shaun5 小时前
STL：string和vector
开发语言·数据结构·c++·算法·leetcode
winfield8215 小时前
滑动时间窗口，找一段区间中的最大值
数据结构·算法
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击05在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）06Gemini3 生成的基于手势控制3D粒子圣诞树07解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题08Labelme从安装到标注：零基础完整指南09CentOS的ISO镜像下载10GLM-4.7 vs MiniMax-M2.1：代码工程理解