从入门到精通：周志华《机器学习》第一、二章深度解析

从入门到精通：周志华《机器学习》前两章深度解析

作为机器学习领域的经典教材，周志华老师的《机器学习》（俗称"西瓜书"）前两章为整个学科搭建了核心框架------第一章奠定基础概念与思想，第二章聚焦模型评估的科学方法。这两章看似基础，却暗藏机器学习的核心逻辑：如何从数据中学习有效模型，又如何客观判断模型的好坏 。本文将跳出原文复述，从"概念本质→公式拆解→实例验证→习题解析"四个维度，带你吃透前两章的核心知识。

第一章绪论：机器学习的本质与核心思想

1.1 机器学习的本质：让计算机"从经验中学习"

机器学习的核心定义可概括为：通过计算手段，利用数据（经验）改善系统性能。通俗来讲，就是让计算机像人一样"吃一堑长一智"------比如通过学习大量西瓜的特征（色泽、根蒂、敲声）和标签（好瓜/坏瓜），自动总结规律，进而判断新西瓜的好坏。

关键补充：Mitchell的形式化定义（经典且必考）

若用 P P P评估程序在任务 T T T上的性能，程序通过经验 E E E使 P P P提升，则称程序对 E E E进行了学习。

例子：任务 T T T= 西瓜分类，经验 E E E= 17个标注好的西瓜样本，性能 P P P= 分类准确率。程序通过学习 E E E，准确率从60%提升到85%，即完成了"学习"。

1.2 核心术语：用西瓜例子逐个对应

术语	定义（通俗版）	西瓜数据集对应实例
数据集 D D D	所有样本的集合	17个西瓜的完整记录（编号1-17）
样本 x i x_i xi	单个对象的描述（属性组合）	编号1的西瓜：(色泽=青绿, 根蒂=蜷缩, 敲声=浊响)
属性/特征	描述对象的维度	色泽、根蒂、敲声等
标记 y i y_i yi	样本的"结果"（分类/回归目标）	编号1的西瓜标记："好瓜"
样例 ( x i , y i ) (x_i,y_i) (xi,yi)	带标记的样本	(色泽=青绿, 根蒂=蜷缩, 敲声=浊响, 好瓜)
泛化能力	模型对新样本的预测能力	学好的模型能准确判断没见过的西瓜

1.3 假设空间与版本空间：模型的"搜索范围"

核心逻辑

机器学习的过程本质是在假设空间中搜索与训练集一致的假设：

假设空间：所有可能的"属性→标签"映射（比如"好瓜=色泽青绿 ∧ 根蒂蜷缩""好瓜=色泽* ∧ 根蒂蜷缩"等）。
版本空间：假设空间中与训练集完全匹配的所有假设（即"符合数据规律的所有可能模型"）。

公式/逻辑推导（以西瓜二分类为例）

假设西瓜的3个属性：

色泽：青绿、乌黑、浅白（3种取值+通配符* → 4种可能）
根蒂：蜷缩、硬挺（2种取值+* → 3种可能）
敲声：浊响、沉闷（2种取值+* → 4种可能）
额外考虑"没有好瓜"的极端假设（∅）

则假设空间大小 = 4×3×3 + 1 = 37（所有组合+极端假设）。

版本空间实例（训练集：编号1"好瓜"、编号4"坏瓜"）

编号1：(青绿, 蜷缩, 浊响)→好瓜 → 排除与该组合矛盾的假设（如"色泽乌黑→好瓜"）
编号4：(青绿, 蜷缩, 沉闷)→坏瓜 → 排除"色泽青绿 ∧ 根蒂蜷缩 ∧ 敲声*→好瓜"的假设
最终版本空间（部分）：
1. (色泽=青绿, 根蒂=蜷缩, 敲声=浊响)→好瓜
2. (色泽=青绿, 根蒂=*, 敲声=浊响)→好瓜
3. (色泽=*, 根蒂=蜷缩, 敲声=浊响)→好瓜

1.4 归纳偏好：模型的"选择标准"

核心问题

版本空间中存在多个有效假设（比如上面3个假设），模型必须选一个------归纳偏好就是模型的"选择偏好"。

关键公式：奥卡姆剃刀原则

"若多个假设与观察一致，选最简单的那个"。

例子：上面3个假设中，"(色泽=*, 根蒂=蜷缩, 敲声=浊响)→好瓜"更简单（通配符更多，适用范围更广），模型会优先选择。

NFL定理（没有免费的午餐）

核心结论：脱离具体问题，所有算法的期望性能相同。

公式拆解：
泛化误差期望 E o t e ( L a ∣ X , f ) = ∑ h ∑ x ∈ X − X P ( x ) I ( h ( x ) ≠ f ( x ) ) P ( h ∣ X , L a ) E_{ote}(\mathfrak{L}a|X,f) = \sum_h \sum{x\in X-X} P(x)\mathbb{I}(h(x)\neq f(x))P(h|X,\mathfrak{L}_a) Eote(La∣X,f)=∑h∑x∈X−XP(x)I(h(x)=f(x))P(h∣X,La)
- L a \mathfrak{L}_a La：学习算法 a a a
- X X X：训练集， X − X X-X X−X：测试集
- h h h：假设， f f f：真实目标函数
- I ( ⋅ ) \mathbb{I}(·) I(⋅)：指示函数（真=1，假=0）
通俗理解：如果所有问题出现概率相同，"随机猜"和"深度学习"的平均性能一样------但现实中我们只关注具体问题（比如西瓜分类），因此算法偏好需匹配问题特性。

第二章模型评估与选择：如何科学判断模型好坏

2.1 误差与过拟合：模型的"常见陷阱"

经验误差（训练误差）：模型在训练集上的误差（比如训练集17个西瓜，错分3个 → 经验误差=3/17≈17.6%）。
泛化误差：模型在新样本上的误差（核心关注目标）。
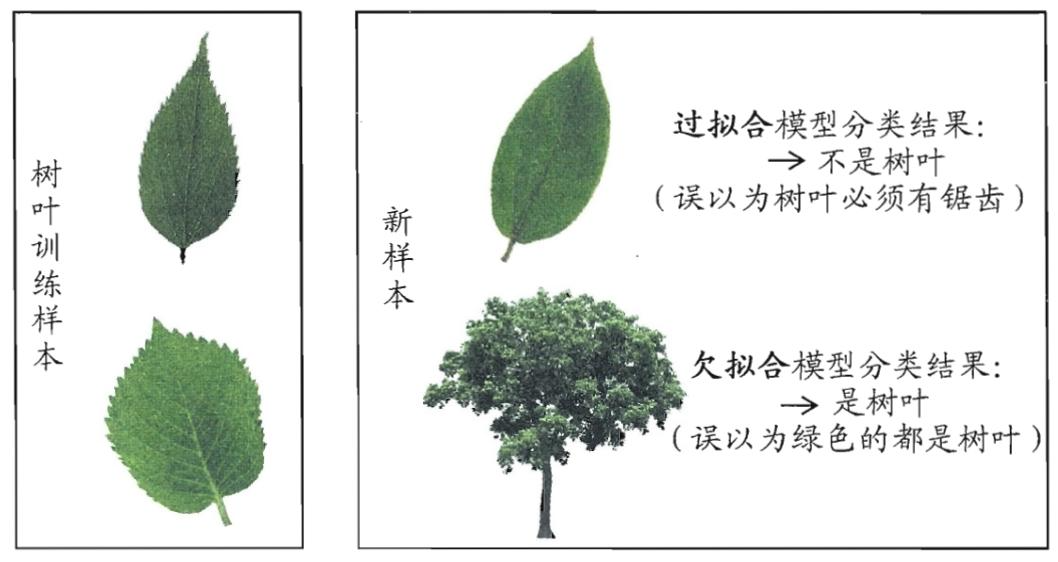
过拟合：模型"死记硬背"训练集（比如记住每个西瓜的编号），经验误差极低但泛化误差极高（遇到新西瓜就失效）。
欠拟合：模型没学会规律（比如只看色泽判断西瓜，忽略根蒂、敲声），经验误差和泛化误差都高。

2.2 评估方法：如何公平测试模型

1. 留出法（Hold-out）

核心逻辑：将数据集按比例划分为训练集（70%-80%）和测试集（20%-30%），训练集学模型，测试集估泛化误差。
关键要求：分层采样（保持类别比例）。
例子：1000个样本（500正/500反），分层采样后训练集700（350正/350反），测试集300（150正/150反）------避免测试集全是反例导致误差估计失真。

伪代码逻辑：

python 复制代码

def hold_out(D, test_ratio=0.3):
    # 分层采样划分训练集S和测试集T
    S_pos = 分层采样(D_pos, len(D_pos)*(1-test_ratio))
    S_neg = 分层采样(D_neg, len(D_neg)*(1-test_ratio))
    T_pos = D_pos - S_pos
    T_neg = D_neg - S_neg
    S = S_pos ∪ S_neg
    T = T_pos ∪ T_neg
    # 训练模型并评估
    model = train(S)
    error = evaluate(model, T)
    return error

注意：需重复多次划分取平均（比如100次），避免单次划分的随机性影响结果。

2. 交叉验证法（k-折交叉验证）

核心逻辑：将数据集划分为k个大小相似的子集，轮流用k-1个子集训练，1个子集测试，最终取k次误差的平均。
常用k=10（10折交叉验证）：
例子：100个样本划分为10个子集（各10个），第1次用子集1-9训练、子集10测试，第2次用子集1-8+10训练、子集9测试......共10次，误差平均为最终结果。
留一法（LOO）：k=m（样本数），每次留1个样本测试------无随机误差，但计算量大（m=1万需训练1万次）。

3. 自助法（Bootstrapping）

核心逻辑：有放回采样生成训练集 D ′ D' D′（m个样本），未被采样的样本（约36.8%）作为测试集。
公式：样本未被采样的概率 lim ⁡ m → ∞ ( 1 − 1 / m ) m = 1 / e ≈ 0.368 \lim_{m→∞}(1-1/m)^m = 1/e ≈ 0.368 limm→∞(1−1/m)m=1/e≈0.368
- 例子：m=1000，采样1000次，约632个样本被选中（可能重复），368个未被选中作为测试集。
适用场景：数据集小时（比如m<100），避免训练集过小导致的偏差。

2.3 性能度量：量化模型的"好坏标准"

1. 回归任务：均方误差（MSE）

公式： E ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 E(f;D) = \frac{1}{m}\sum_{i=1}^m (f(x_i)-y_i)^2 E(f;D)=m1∑i=1m(f(xi)−yi)2
符号拆解：
- f ( x i ) f(x_i) f(xi)：模型对第i个样本的预测值
- y i y_i yi：第i个样本的真实值
- m m m：样本总数
- 平方：消除正负误差抵消，放大极端误差
例子：3个西瓜的成熟度预测
- 真实值 y = [ 0.9 , 0.7 , 0.8 ] y = [0.9, 0.7, 0.8] y=[0.9,0.7,0.8]
- 预测值 f ( x ) = [ 0.8 , 0.6 , 0.7 ] f(x) = [0.8, 0.6, 0.7] f(x)=[0.8,0.6,0.7]
- 计算： ( 0. 1 2 + 0. 1 2 + 0. 1 2 ) / 3 = 0.01 (0.1² + 0.1² + 0.1²)/3 = 0.01 (0.12+0.12+0.12)/3=0.01→ 均方误差越小，模型越优。

2. 分类任务：查准率（P）、查全率（R）与F1

混淆矩阵（二分类）：

真实\预测正例（好瓜）反例（坏瓜）

正例 TP（真阳性） FN（假阴性）

反例 FP（假阳性） TN（真阴性）
- 例子：10个西瓜预测，TP=4（真好瓜），FP=1（假好瓜），FN=2（假坏瓜），TN=3（真坏瓜）
查准率（P）：预测为正例的样本中，真实正例的比例

公式： P = T P T P + F P P = \frac{TP}{TP+FP} P=TP+FPTP

例子： P = 4 / ( 4 + 1 ) = 80 % P = 4/(4+1) = 80\% P=4/(4+1)=80%→ 挑出的"好瓜"中80%是真的。
查全率（R）：真实正例中，被预测为正例的比例

公式： R = T P T P + F N R = \frac{TP}{TP+FN} R=TP+FNTP

例子： R = 4 / ( 4 + 2 ) ≈ 66.7 % R = 4/(4+2) ≈ 66.7\% R=4/(4+2)≈66.7% → 所有真好瓜中66.7%被挑出来了。
F1分数（平衡P和R）：

公式： F 1 = 2 P R P + R 例子： F1 = \frac{2PR}{P+R} 例子： F1=P+R2PR例子：F1 = 2×0.8×0.667/(0.8+0.667) ≈ 72.7%$ → F1越高，P和R越均衡。

真实\预测	正例（好瓜）	反例（坏瓜）
正例	TP（真阳性）	FN（假阴性）
反例	FP（假阳性）	TN（真阴性）

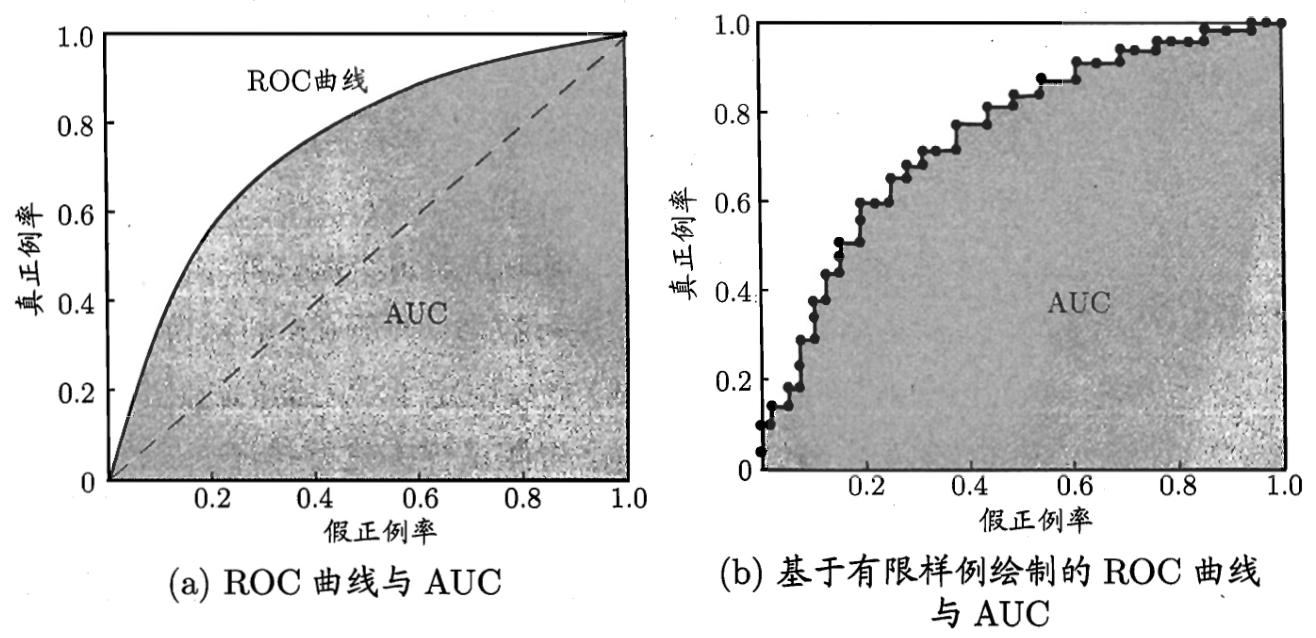
3. ROC与AUC

核心逻辑：基于模型的预测概率排序，绘制"真正例率（TPR）-假正例率（FPR）"曲线。
关键公式：
- T P R = T P T P + F N TPR = \frac{TP}{TP+FN} TPR=TP+FNTP（真实正例的识别率，查全率）
- F P R = F P T N + F P FPR = \frac{FP}{TN+FP} FPR=TN+FPFP（真实反例被误判为正例的比例）
AUC：ROC曲线下的面积（0-1之间），AUC越大，模型排序能力越强。
例子：AUC=0.9 → 随机选一个正例和一个反例，模型将正例排在前面的概率为90%。

2.4 偏差-方差分解：泛化误差的"本质来源"

核心公式（回归任务）

E ( f ; D ) = b i a s 2 ( x ) + v a r ( x ) + ε 2 E(f;D) = bias²(x) + var(x) + \varepsilon² E(f;D)=bias2(x)+var(x)+ε2

符号拆解：
- b i a s 2 ( x ) = ( f ˉ ( x ) − y ) 2 bias²(x) = (\bar{f}(x)-y)^2 bias2(x)=(fˉ(x)−y)2：偏差（模型期望预测与真实值的差距 → 欠拟合程度）
- v a r ( x ) = E D [ ( f ( x ; D ) − f ˉ ( x ) ) 2 ] var(x) = E_D[(f(x;D)-\bar{f}(x))^2] var(x)=ED[(f(x;D)−fˉ(x))2]：方差（不同训练集导致的模型波动 → 过拟合程度）
- ε 2 = E D [ ( y D − y ) 2 ] \varepsilon² = E_D[(y_D-y)^2] ε2=ED[(yD−y)2]：噪声（数据本身的不可避免误差 → 下界）
直观理解：
- 欠拟合模型：bias大，var小（比如只用色泽判断西瓜，无论怎么换训练集，误差都高）。
- 过拟合模型：var大，bias小（比如记住每个西瓜的编号，换训练集后误差波动大）。

前两章课后习题详细解答

第一章习题

1.1 题干：表1.1中若只包含编号为1和4的两个样例，试给出相应的版本空间。

解答：

明确假设空间构成：

色泽（青绿、乌黑、浅白、）× 根蒂（蜷缩、稍蜷、硬挺、）× 敲声（浊响、沉闷、清脆、*）+ 极端假设∅，共4×4×4+1=65种假设。
训练集约束：
- 编号1：(色泽=青绿, 根蒂=蜷缩, 敲声=浊响)→好瓜
- 编号4：(色泽=青绿, 根蒂=蜷缩, 敲声=沉闷)→坏瓜
筛选有效假设（与训练集一致）：
- 必须满足：色泽=青绿 ∧ 根蒂=蜷缩时，仅敲声=浊响→好瓜，其他敲声→坏瓜。
- 版本空间（核心假设）：
  1. (色泽=青绿, 根蒂=蜷缩, 敲声=浊响)→好瓜
  2. (色泽=青绿, 根蒂=*, 敲声=浊响)→好瓜
  3. (色泽=*, 根蒂=蜷缩, 敲声=浊响)→好瓜
  4. (色泽=青绿, 根蒂=蜷缩, 敲声=*)→坏瓜（排除，与编号1矛盾）
  5. 极端假设∅（排除，因存在好瓜）
最终版本空间为上述1-3条假设及所有包含这些约束的组合（如(色泽=, 根蒂=, 敲声=浊响)→好瓜，需验证是否符合约束：当色泽=青绿、根蒂=蜷缩时，敲声=浊响→好瓜，符合；其他色泽/根蒂时无约束，有效）。

1.2 题干：与使用单个合取式来进行假设表示相比，使用"析合范式"将使得假设空间具有更强的表示能力。例如好瓜↔((色泽=)∧(根蒂=蜷缩)∧(敲声=))∨((色泽=乌黑)∧(根蒂=*)∧(敲声=沉闷))，会把(色泽=青绿∧根蒂=蜷缩∧敲声=清脆)和(色泽=乌黑∧根蒂=硬挺∧敲声=沉闷)都分类为"好瓜"。若使用最多包含k个合取式的析合范式来表达表1.1西瓜分类问题的假设空间，试估算共有多少种可能的假设。

解答：

单个合取式假设空间大小：65（含∅）。
析合范式定义：k个合取式用∨连接（允许重复，但需去重）。
估算逻辑：
- 不考虑冗余（如(A∨A)等价于A），最多包含k个合取式的析合范式数目 = ∑ i = 1 k C 65 i \sum_{i=1}^k C_{65}^i ∑i=1kC65i（从65个合取式中选i个组合）。
- 考虑冗余（如(A∨(A∧B))等价于A），实际数目会减少，但题目仅要求估算，故取上界。
结果：当k=2时，数目≈65 + 65×64/2=2145；k=3时≈65+2145+65×64×63/(6)=45130，以此类推（核心是析合范式通过"或"操作扩展了假设的表达范围）。

1.3 题干：若数据包含噪声，则假设空间中有可能不存在与所有训练样本都一致的假设。在此情形下，试设计一种归纳偏好用于假设选择。

解答：

设计思路：噪声导致"完美假设"不存在，偏好应优先"容错性强、简单性高"的假设，具体如下：

最小化经验误差：选择在训练集上错分样本最少的假设（容忍少量噪声导致的错误）。
奥卡姆剃刀原则：若多个假设经验误差相同，选择最简单的（如合取式最少、通配符最多的假设）。
示例：训练集有1个噪声样本（好瓜被标为坏瓜），两个假设A（错分1个）和B（错分2个），优先选A；若A和C均错分1个，A是"(色泽=*∧根蒂=蜷缩∧敲声=浊响)→好瓜"，C是"(色泽=青绿∧根蒂=蜷缩∧敲声=浊响)∨(色泽=乌黑∧根蒂=稍蜷∧敲声=沉闷)→好瓜"，优先选A（更简单）。

1.4 题干：本章1.4节在论述"没有免费的午餐"定理时，默认使用了"分类错误率"作为性能度量来对分类器进行评估，若换用其他性能度量ℓ则式(1.1)将改为 E o t e ( L a ∣ X , f ) = ∑ h ∑ x ∈ X − X P ( x ) ℓ ( h ( x ) , f ( x ) ) P ( h ∣ X , L a ) E_{ote}(\mathfrak{L}a|X,f) = \sum_h \sum{x\in X-X} P(x)\ell(h(x),f(x))P(h|X,\mathfrak{L}_a) Eote(La∣X,f)=∑h∑x∈X−XP(x)ℓ(h(x),f(x))P(h∣X,La)，试证明"没有免费的午餐定理"仍成立。

证明：

核心前提：所有真实目标函数f均匀分布（NFL定理的核心假设）。
对所有f求和：
∑ f E o t e ( L a ∣ X , f ) = ∑ f ∑ h ∑ x P ( x ) ℓ ( h ( x ) , f ( x ) ) P ( h ∣ X , L a ) \sum_f E_{ote}(\mathfrak{L}_a|X,f) = \sum_f \sum_h \sum_x P(x)\ell(h(x),f(x))P(h|X,\mathfrak{L}_a) f∑Eote(La∣X,f)=f∑h∑x∑P(x)ℓ(h(x),f(x))P(h∣X,La)
交换求和顺序：
= ∑ x P ( x ) ∑ h P ( h ∣ X , L a ) ∑ f ℓ ( h ( x ) , f ( x ) ) = \sum_x P(x) \sum_h P(h|X,\mathfrak{L}_a) \sum_f \ell(h(x),f(x)) =x∑P(x)h∑P(h∣X,La)f∑ℓ(h(x),f(x))
关键观察：由于f均匀分布，对任意h(x)和x， ∑ f ℓ ( h ( x ) , f ( x ) ) \sum_f \ell(h(x),f(x)) ∑fℓ(h(x),f(x))是常数（与h和 L a \mathfrak{L}_a La无关）------因为f(x)的所有可能取值等概率出现，ℓ的求和结果固定。
化简：
= ∑ x P ( x ) ⋅ C ⋅ ∑ h P ( h ∣ X , L a ) = C ⋅ ∑ x P ( x ) ⋅ 1 = C = \sum_x P(x) \cdot C \cdot \sum_h P(h|X,\mathfrak{L}_a) = C \cdot \sum_x P(x) \cdot 1 = C =x∑P(x)⋅C⋅h∑P(h∣X,La)=C⋅x∑P(x)⋅1=C
其中C是常数，与算法 L a \mathfrak{L}_a La无关。
结论：对任意算法 L a \mathfrak{L}_a La和 L b \mathfrak{L}b Lb， ∑ f E o t e ( L a ∣ X , f ) = ∑ f E o t e ( L b ∣ X , f ) \sum_f E{ote}(\mathfrak{L}a|X,f) = \sum_f E{ote}(\mathfrak{L}_b|X,f) ∑fEote(La∣X,f)=∑fEote(Lb∣X,f)，NFL定理仍成立。

1.5 题干：试述机器学习能在互联网搜索的哪些环节起什么作用。

解答：

查询理解：通过机器学习分析用户查询意图（如"苹果"是水果还是手机），基于历史查询-点击数据训练分类模型，提升意图识别准确率。
网页排序：核心应用（如谷歌的PageRank+机器学习模型），通过分析网页内容、用户点击行为、链接关系等特征，训练排序模型，将最相关的网页排在前面。
广告推荐：根据用户兴趣和查询内容，训练推荐模型，匹配相关广告（如搜索"旅游"时推荐机票广告），提升广告点击率。
拼写纠错：基于用户输入错误样本（如"激浪"→"机票"），训练纠错模型，自动修正拼写错误，提升搜索体验。
图片/视频搜索：通过图像识别、视频内容分析的机器学习模型，将图片/视频的视觉特征与查询匹配（如搜索"夕阳"时返回含夕阳的图片）。

第二章习题

2.1 题干：数据集包含1000个样本，其中500个正例、500个反例，将其划分为包含70%样本的训练集和30%样本的测试集用于留出法评估，试估算共有多少种划分方式。

解答：

关键要求：分层采样（保持正反例比例），训练集700个（350正+350反），测试集300个（150正+150反）。
计算逻辑：
- 从500正例中选350个的组合数： C 500 350 C_{500}^{350} C500350
- 从500反例中选350个的组合数： C 500 350 C_{500}^{350} C500350
- 总划分方式 = C 500 350 × C 500 350 C_{500}^{350} \times C_{500}^{350} C500350×C500350
简化说明：
- 组合数公式 C n k = n ! k ! ( n − k ) ! C_n^k = \frac{n!}{k!(n-k)!} Cnk=k!(n−k)!n!，此处无需计算具体数值，核心是"分层采样后的组合数乘积"。
- 若不分层采样（错误做法），总方式为 C 1000 700 C_{1000}^{700} C1000700，但会导致训练集/测试集类别比例失衡（如训练集全是正例），因此必须分层。

2.2 题干：数据集包含100个样本，其中正、反例各一半，假定学习算法所产生的模型是将新样本预测为训练样本数较多的类别（训练样本数相同时进行随机猜测），试给出用10折交叉验证法和留一法分别对错误率进行评估所得的结果。

解答：

10折交叉验证法：
- 划分方式：100个样本分为10折（每折10个，5正5反）。
- 训练过程：每次用9折（90个样本，45正45反）训练，模型因正反例数相同，随机猜测（准确率50%）。
- 测试过程：测试集10个样本（5正5反），随机猜测的错误率=50%。
- 结果：10次验证的错误率均为50%，最终评估错误率=50%。
留一法：
- 划分方式：每次留1个样本测试，训练集99个样本（49正50反或50正49反）。
- 训练过程：
  - 若测试样本是正例：训练集49正50反 → 反例数多，模型预测为反例 → 错误（正例被误判）。
  - 若测试样本是反例：训练集50正49反 → 正例数多，模型预测为正例 → 错误（反例被误判）。
- 测试过程：100次测试中，所有样本均被误判，错误率=100%。
- 关键原因：留一法的训练集永远少1个样本，导致类别比例失衡，模型始终预测多数类，而测试样本是少数类，因此全错。

2.3 题干：若学习器A的F1值比学习器B高，试析A的BEP值是否也比B高。

解答：

不一定。原因如下：

BEP（平衡点）：P=R时的取值，反映P和R的均衡性；F1是P和R的调和平均，同样反映均衡性，但二者的计算逻辑不同。
反例：
- 学习器A：P=0.8，R=0.6 → F1=2×0.8×0.6/(0.8+0.6)≈0.686；BEP=0.7（假设P=R=0.7时的性能）。
- 学习器B：P=0.7，R=0.7 → F1=0.7；BEP=0.7。
  此时A的F1（0.686）< B的F1（0.7），BEP相同。
- 另一反例：A的P=0.9，R=0.5 → F1≈0.643；BEP=0.6；B的P=0.75，R=0.65 → F1≈0.696；BEP=0.7。此时A的F1 < B的F1，BEP也更小。
结论：F1与BEP正相关但非严格单调，需结合P-R曲线的形状判断，不能仅凭F1高低推断BEP。

2.4 题干：试述真正例率(TPR)、假正例率(FPR)与查准率§、查全率®之间的联系。

解答：

定义回顾：
- TPR = TP/(TP+FN)（查全率R，真实正例的识别率）
- FPR = FP/(TN+FP)（真实反例被误判为正例的比例）
- P = TP/(TP+FP)（预测正例中的真实正例比例）
- R = TPR（二者定义完全相同）
核心联系：
- R与TPR等价：查全率就是真正例率，只是应用场景表述不同（R侧重"检索/分类的完整性"，TPR侧重"ROC曲线的纵轴"）。
- P与TPR/FPR的关系：P与TPR正相关、与FPR负相关。
  例子：TP=4，FN=2（TPR=4/6≈66.7%），若FP从1增加到3（FPR从1/(1+3)=25%增加到3/(3+1)=75%），则P从4/(4+1)=80%下降到4/(4+3)≈57.1%。
- 本质：TPR和FPR描述模型对"真实类别"的识别能力，P描述模型预测结果的"精准度"，三者共同反映二分类模型的性能。

2.5 题干：试证明式(2.22)（ A U C = 1 − ℓ r a n k AUC=1-ℓ_rank AUC=1−ℓrank）。

证明：

定义回顾：
- ℓ_rank：排序损失， ℓ r a n k = 1 m + m − ∑ x + ∈ D + ∑ x − ∈ D − [ I ( f ( x + ) < f ( x − ) ) + 0.5 I ( f ( x + ) = f ( x − ) ) ] \ell_rank = \frac{1}{m^+m^-} \sum_{x^+\in D^+} \sum_{x^-\in D^-} [\mathbb{I}(f(x^+)<f(x^-)) + 0.5\mathbb{I}(f(x^+)=f(x^-))] ℓrank=m+m−1∑x+∈D+∑x−∈D−[I(f(x+)<f(x−))+0.5I(f(x+)=f(x−))]
- AUC：ROC曲线下面积，反映正例排在反例前面的概率。
关键观察：
- 对任意一对正例x⁺和反例x⁻，有三种情况：
  1. f(x⁺) > f(x⁻)：正例排前面，贡献0到ℓ_rank，贡献1到AUC。
  2. f(x⁺) < f(x⁻)：正例排后面，贡献1到ℓ_rank，贡献0到AUC。
  3. f(x⁺) = f(x⁻)：贡献0.5到ℓ_rank，贡献0.5到AUC。
量化关系：
- 所有x⁺和x⁻对的总贡献：
  ∑ x + , x − [ I ( f ( x + ) > f ( x − ) ) + 0.5 I ( f ( x + ) = f ( x − ) ) ] = m + m − ( 1 − ℓ r a n k ) \sum_{x^+,x^-} [\mathbb{I}(f(x^+)>f(x^-)) + 0.5\mathbb{I}(f(x^+)=f(x^-))] = m^+m^-(1 - \ell_rank) x+,x−∑[I(f(x+)>f(x−))+0.5I(f(x+)=f(x−))]=m+m−(1−ℓrank)
- 而AUC的定义正是"正例排前面的概率"，即：
  A U C = 1 m + m − ∑ x + , x − [ I ( f ( x + ) > f ( x − ) ) + 0.5 I ( f ( x + ) = f ( x − ) ) ] AUC = \frac{1}{m^+m^-} \sum_{x^+,x^-} [\mathbb{I}(f(x^+)>f(x^-)) + 0.5\mathbb{I}(f(x^+)=f(x^-))] AUC=m+m−1x+,x−∑[I(f(x+)>f(x−))+0.5I(f(x+)=f(x−))]
- 代入上式得： A U C = 1 − ℓ r a n k AUC = 1 - \ell_rank AUC=1−ℓrank，证明完毕。

2.6 题干：试述错误率与ROC曲线的联系。

解答：

错误率：全局性能度量， E = F P + F N m E = \frac{FP+FN}{m} E=mFP+FN（二分类），反映整体错分比例。
ROC曲线：局部性能度量，描述"不同阈值下TPR与FPR的 trade-off"。
核心联系：
- 错误率对应ROC曲线上的一个点：给定分类阈值，确定TP、FP、TN、FN，计算错误率；不同阈值对应ROC曲线上的不同点。
- 错误率受类别比例影响，ROC曲线不受：例如正例占10%，错误率= (FP+FN)/100，而ROC曲线仅关注TPR和FPR（与类别比例无关）。
- 示例：模型A错误率=20%，模型B错误率=25%，但A的ROC曲线可能被B包住（A在高TPR区间表现更好）------说明错误率不能反映模型在不同场景下的性能，而ROC曲线更全面。

2.7 题干：试证明任意一条ROC曲线都有一条代价曲线与之对应，反之亦然。

证明：

必要性（ROC曲线→代价曲线）：
- ROC曲线上任一点(x,FPR)、(y,TPR)，对应FNR=1-TPR。
- 代价曲线的横轴：正例概率代价 P ( + ) c o s t = p ⋅ c o s t 01 p ⋅ c o s t 01 + ( 1 − p ) ⋅ c o s t 10 P(+)cost = \frac{p \cdot cost_{01}}{p \cdot cost_{01} + (1-p) \cdot cost_{10}} P(+)cost=p⋅cost01+(1−p)⋅cost10p⋅cost01（p为正例概率）。
- 代价曲线的纵轴：归一化代价 c o s t n o r m = F N R ⋅ p ⋅ c o s t 01 + F P R ⋅ ( 1 − p ) ⋅ c o s t 10 p ⋅ c o s t 01 + ( 1 − p ) ⋅ c o s t 10 cost_{norm} = \frac{FNR \cdot p \cdot cost_{01} + FPR \cdot (1-p) \cdot cost_{10}}{p \cdot cost_{01} + (1-p) \cdot cost_{10}} costnorm=p⋅cost01+(1−p)⋅cost10FNR⋅p⋅cost01+FPR⋅(1−p)⋅cost10。
- 对ROC曲线上的每个点，给定p和cost矩阵，可唯一计算出cost_{norm}，从而绘制代价曲线的线段；所有线段的下界构成代价曲线，故ROC曲线可唯一确定代价曲线。
充分性（代价曲线→ROC曲线）：
- 代价曲线的每条线段对应ROC曲线上的一个点(FPR, TPR)。
- 对任意p和cost矩阵，cost_{norm}与FPR、FNR线性相关，通过调整p和cost矩阵，可解出FPR和TPR，从而反向确定ROC曲线上的点。
- 遍历所有可能的p和cost矩阵，可恢复完整的ROC曲线，故代价曲线可唯一确定ROC曲线。
结论：ROC曲线与代价曲线是一一对应的，可相互推导。

2.8 题干：Min-max规范化和z-score规范化是两种常用的规范化方法。令x和x'分别表示变量在规范化前后的取值，相应的，令 x m i n x_min xmin和 x m a x x_max xmax表示规范化前的最小值和最大值， x m ′ i n x'_min xm′in和 x m ′ a x x'_max xm′ax表示规范化后的最小值和最大值， x ˉ \bar{x} xˉ和 σ x σ_x σx分别表示规范化前的均值和标准差，则min-max规范化、z-score规范化分别如式(2.43)和(2.44)所示。试析二者的优缺点。

解答：

Min-max规范化（线性缩放至[x'_min, x'_max]）：
x ′ = x m ′ i n + x − x m i n x m a x − x m i n × ( x m ′ a x − x m ′ i n ) x' = x'_min + \frac{x - x_min}{x_max - x_min} \times (x'_max - x'_min) x′=xm′in+xmax−xminx−xmin×(xm′ax−xm′in)
- 优点：
  - 保持数据的原始分布趋势，无失真。
  - 结果在固定区间内，适合要求数据范围明确的场景（如神经网络输入）。
- 缺点：
  - 对异常值敏感：若数据含极端值（如x_max=1000，其他值<100），会导致大部分数据被压缩到小范围。
  - 依赖训练集的x_min和x_max：新样本超出范围时，需重新计算x_min和x_max。
z-score规范化（标准化为均值0、标准差1）：
x ′ = x − x ˉ σ x x' = \frac{x - \bar{x}}{\sigma_x} x′=σxx−xˉ
- 优点：
  - 抗异常值：通过均值和标准差标准化，极端值影响较小。
  - 不依赖数据范围：适合不同尺度变量的融合（如身高cm和体重kg）。
  - 新样本可直接应用，无需重新计算参数。
- 缺点：
  - 改变数据的原始分布范围，结果无固定区间。
  - 若数据不服从正态分布，标准化效果可能不佳。

2.9 题干：试述χ²检验过程。

解答：

χ²检验（卡方检验）用于比较两个分类器的性能差异（基于列联表），步骤如下：

构建列联表（二分类器A和B的分类结果）：

算法B\算法A 正确错误

正确 a b

错误 c d
- a：A和B都正确的样本数
- b：A错误、B正确的样本数
- c：A正确、B错误的样本数
- d：A和B都错误的样本数
提出假设：
- 原假设H0：A和B的性能无显著差异（b=c）。
- 备择假设H1：A和B的性能有显著差异（b≠c）。
计算χ²统计量：
χ 2 = ( ∣ b − c ∣ − 1 ) 2 b + c \chi^2 = \frac{(|b - c| - 1)^2}{b + c} χ2=b+c(∣b−c∣−1)2
- 减1是连续性修正（因b和c是离散值，χ²分布是连续分布）。
确定临界值：
- 自由度df=1（列联表为2×2），显著水平α=0.05时，临界值χ²₀.₀₅(1)=3.8415。
决策：
- 若χ² > 临界值：拒绝H0，认为A和B性能有显著差异。
- 若χ² ≤ 临界值：接受H0，认为无显著差异。

算法B\算法A	正确	错误
正确	a	b
错误	c	d

2.10 题干：试述在Friedman检验中使用式(2.34)与(2.35)的区别。

解答：

Friedman检验用于比较多个算法在多个数据集上的性能，两式的区别如下：

式(2.34)（原始Friedman检验）：
τ χ 2 = 12 N k ( k + 1 ) ( ∑ i = 1 k r i 2 − k ( k + 1 ) 2 4 ) \tau_{\chi^2} = \frac{12N}{k(k+1)} \left( \sum_{i=1}^k r_i^2 - \frac{k(k+1)^2}{4} \right) τχ2=k(k+1)12N(i=1∑kri2−4k(k+1)2)
- 适用场景：数据集数N较大（N→∞），τχ²服从自由度k-1的χ²分布。
- 缺点：过于保守（拒绝原假设的门槛高），当N较小时（如N<20），检验效能低（易误判无显著差异）。
式(2.35)（修正Friedman检验，F分布）：

τ F = ( N − 1 ) τ χ 2 N ( k − 1 ) − τ χ 2 \tau_F = \frac{(N-1)\tau_{\chi^2}}{N(k-1) - \tau_{\chi^2}} τF=N(k−1)−τχ2(N−1)τχ2

适用场景：N和k适中（实际常用），τF服从自由度(k-1, (k-1)(N-1))的F分布。
优点：克服原始检验的保守性，检验效能更高（更易识别真实的性能差异）。

核心区别：
- 分布不同：χ²分布 vs F分布。
- 适用场景不同：大N vs 适中N。
- 检验效能不同：原始检验保守 vs 修正检验更灵敏。
- 实际应用：修正检验（式2.35）更常用，因大多数机器学习实验的数据集数N较小（如N<10）。

总结

《机器学习》前两章的本质是"建立机器学习的思维框架"：第一章定义了"什么是机器学习""学习的核心逻辑"（假设空间搜索+归纳偏好），第二章解决了"如何判断模型好坏"（科学的评估方法+性能度量）。这两章的知识是后续所有算法学习的基础------无论学习决策树、神经网络还是SVM，都离不开"泛化能力""过拟合""误差评估"这些核心概念。

参考资料

吃瓜教程：南瓜书 PumpkinBook
视频教程