【数据结构】单链表的经典算法题

1单链表算法题

1.1 移除链表元素

题目链接

思路一：查找值为val的结点并返回结点，返回指定位置的结点

while(遍历)---O(N)
{
 	//查找值为val的结点
 	if()
 	//删除值为val的结点---O(N)
}

思路二：创建新链表，将原链表中不为val结点拿来尾插

//时间复杂度O(N)
//结构体已经定义了
struct ListNode
{
  	int val;
  	struct ListNode* next;
};
typedef struct ListNode ListNode;
struct ListNode* removeElements(struct ListNode* head,int val)
{
    //创建新的链表
    ListNode* newHead,*newTail;
    newHead=newTail=NULL;
    ListNode* pcur=head;
    while(pcur)
    {
        if(pcur->val!=val)
        {
            //尾插
            //链表为空
        	if(newHead==NULL)
                newHead=newTail=pcur;
            else
            {
                //链表非空
                newTail->next=pcur;
                newTail=newTail->next;
            }
        }
        pcur=pcur->next;
    }
    if(newTail)
        newTail->next=NULL;
    return newHead;
}

OJ代码有bug怎么办？VS调试技能⽤起来

1）将OJ代码复制粘贴到vs上

2）创建测试⽅法，调⽤本次要调试的⽬标⽅法

3）利⽤vs调试⼯具排查代码问题

//调试
void test01()
{
    //创建新链表
    ListNode* node1=(ListNode*)malloc(sizeof(ListNode));
    ListNode* node2=(ListNode*)malloc(sizeof(ListNode));
    ListNode* node3=(ListNode*)malloc(sizeof(ListNode));
    ListNode* node4=(ListNode*)malloc(sizeof(ListNode));
    ListNode* node5=(ListNode*)malloc(sizeof(ListNode));
    ListNode* node6=(ListNode*)malloc(sizeof(ListNode));
    ListNode* node7=(ListNode*)malloc(sizeof(ListNode));
    
    node1->val=1;
    node2->val=2;
    node3->val=6;
    node4->val=3;
    node5->val=4;
    node6->val=5;
    node7->val=6;
    
    node1->next=node2;
    node2->next=node3;
    node3->next=node4;
    node4->next=node5;
    node5->next=node6;
    node6->next=node7;
    node7->next=NULL;
    
    ListNode* newHead=removeElements()
}

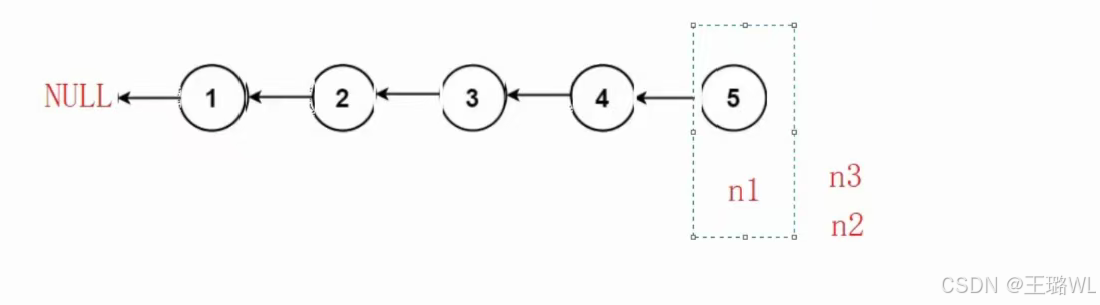
1.2 反转链表

题目链接

思路一：创建新链表，遍历原链表将结点头插到新链表中

时间复杂度O(N)
思路二：

//时间复杂度o(N)
typedef struct ListNode ListNode;
struct ListNode* reverseList(struct ListNode* head)
{
    if(head==NULL)
        return head;
    ListNode* n1,*n2,*n3;
    n1=NULL;
    n2=head;
    n3=n2->next;
    while(n2)//以n2为判断条件，不能以n3为判断条件，因为最后n2的下一个要为NULL，如果n3为判断条件，n2最后不会被赋值
    {
        n2->next=n1;
        n1=n2;
        n2=n3;
        if(n3)
        	n3=n3->next;
    }
    return n1;
}

此时的结果图

1.3 链表的中间结点

题目链接

思路一：求链表总长度，总长度/2再取整就是中间结点位置，遍历找中间结点

while()//求总长度
{
}//size++
int mid=size//2;
while(mid)//根据mid找中间位置

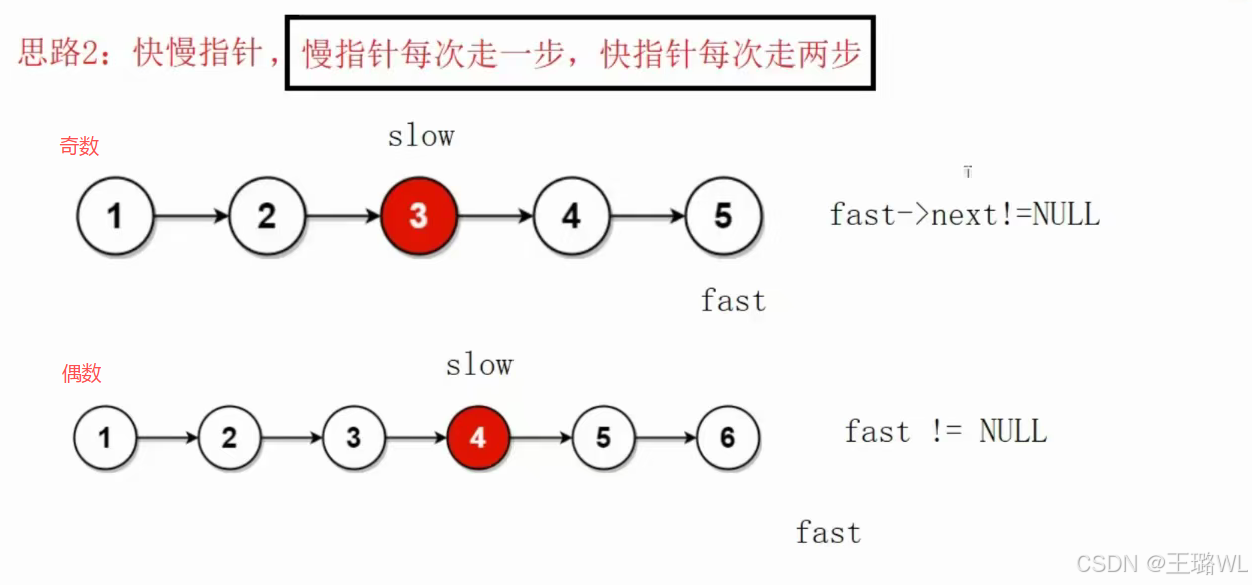
思路二：快慢指针，慢指针每次走一步，快指针每次走两步

typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head)
{
    //创建快慢指针
    ListNode* slow=head;
    ListNode* fast=head;
    while(fast!=NULL&&fast->next!=NULL)
    //不能写成fast->next!=NULL&&fast!=NULL
    //如果是偶数，fast不为空时，会执行fast->next->next，此时是对空指针的解引用
    {
        slow=slow->next;
        fast=fast->next->next;
    }
    return slow;
}

1.4 合并两个有序链表

题目链接

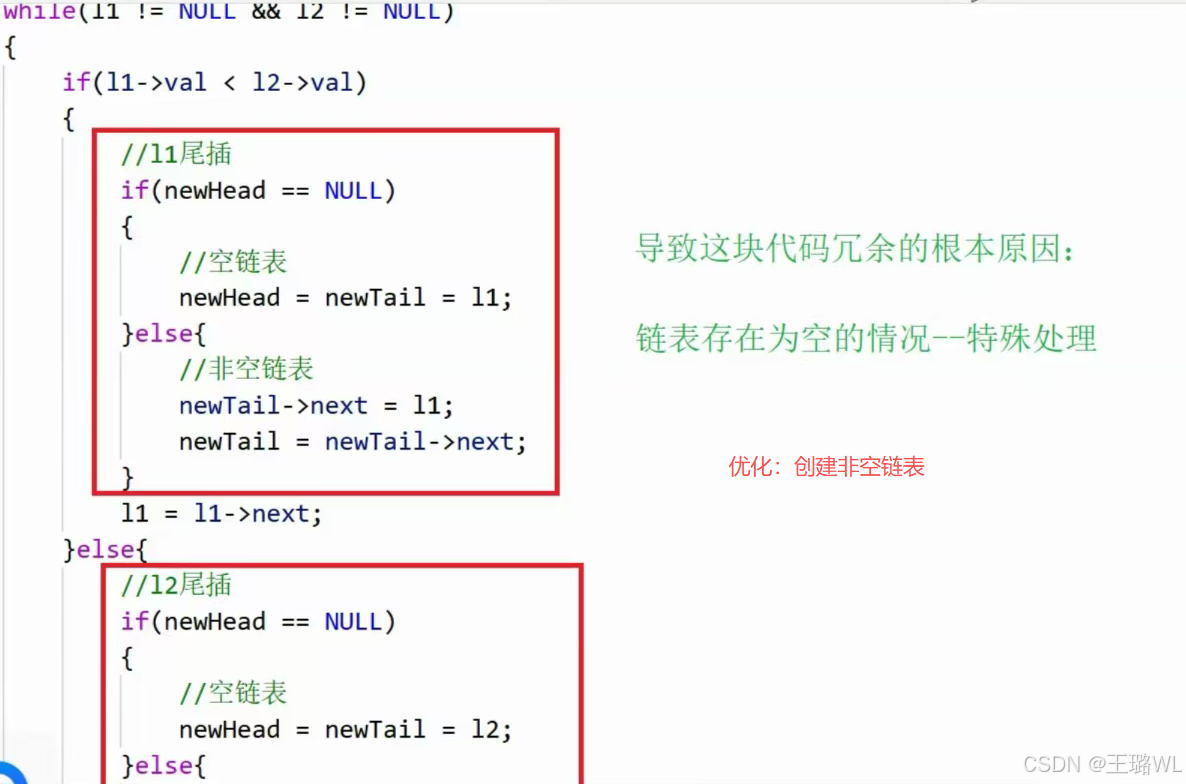
思路：创建新链表，遍历比较，谁小谁往后放

typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1,struct ListNode* list2)
{
    if(list1==NULL)//同时为空也会进入if语句
        return list2;
    if(list==NULL)
        return list1;
    //创建空链表
    ListNode* newnode,*newTail；
    ListNode* l1=list1;
    ListNode* l2=list2;
    while(l1!=NULL&&l2!=NULL)
    {
        if(l1->val<l2->val)
        {
            if(newHead==NULL)
                newHead=newTail=l1;
            else
            {
                newTail->next=l1;
                newTail=newTail->next;
            }
            l1=l1->next;
        }
        else
        {
            if(newHead==NULL)
                newHead=newTail=l2;
            else
            {
                newTail->next=l2;
                newTail=newTail->next;
            }
            l2=l2->next;
        }
    }
    //l1和l2不可能同时为空，除非给了两个空链表
    if(l1)//不需要用while
        newTail->next=l1;//也不需要让newTail=newTail->next，因为l1自带指向
    if(l2)
        newTail->next=l2;
    return newHead;
}

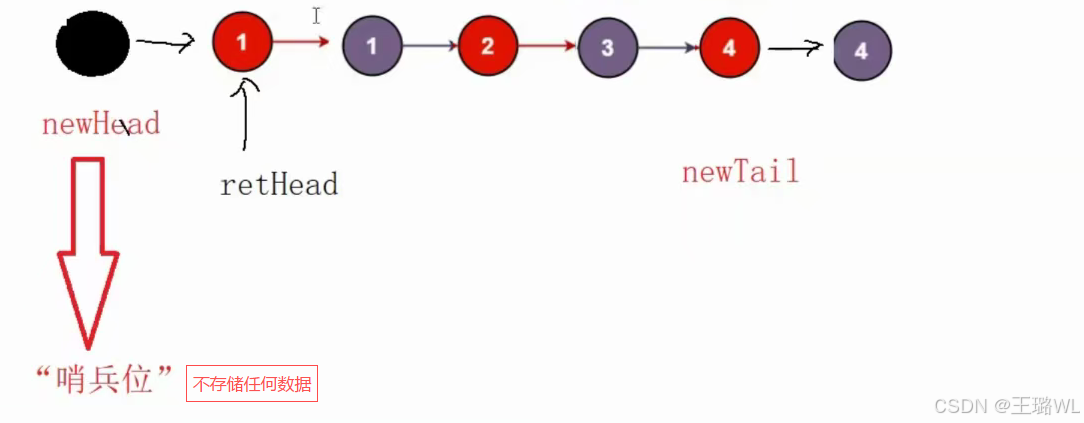
优化如下：

typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1,struct ListNode* list2)
{
    if(list1==NULL)//同时为空也会进入if语句
        return list2;
    if(list==NULL)
        return list1;
    //创建非空链表
    ListNode* newnode,*newTail；
    newHead=newTail=(ListNode*)malloc(sizeof(ListNode));
    while(l1!=NULL&&l2!=NULL)
    {
        if(l1<l2)
        {
            newTail->next=l1;
            newTail=newTail->next;
        	l1=l1->next;
        }
        else
        {
        	newTail->next=l2;
        	newTail=newTail->next;
            l2=l2->next;
        }
    }
    //l1和l2不可能同时为空，除非给了两个空链表
    if(l1)//不需要用while
        newTail->next=l1;//也不需要让newTail=newTail->next，因为l1自带指向
    if(l2)
        newTail->next=l2;
    //newHead是malloc创建的新结点，不是链表的首结点
    ListNode* retHead=newHead->next;//newHead->next才是首结点
    //好习惯是用另一个变量接收首结点地址，再将newHead释放
    free(newHead);
    newHead=NULL;
 return retHead;
}

1.5 链表分割

题目链接

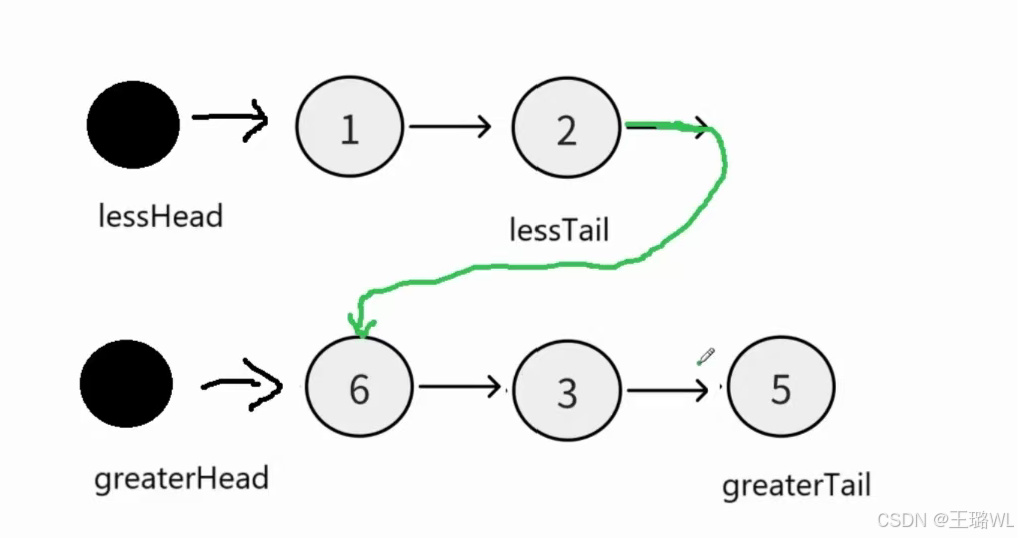
思路：创建两个链表（大链表和小链表），遍历原链表，小的尾插到小链表中，大的尾插到大链表中，最后大小链表首尾相连

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};*/
class Partition {
public:
    ListNode* partition(ListNode* pHead, int x) 
    {
        ListNode* lessHead,*lessTail;
        lessHead=lessTail=(ListNode*)malloc(sizeof(ListNode));
        ListNode* greatHead,* greatTail;
        greatHead=greatTail=(ListNode*)malloc(sizeof(ListNode));
        
        ListNode* pcur=pHead;
        while(pcur)
        {
            if(pcur->val<x)
            {
                //lessHead有头结点，可以直接解引用
                lessTail->next=pcur;
                lessTail=lessTail->next;
            }
            //大于等于都在这里
            else
            {
                greatTail->next=pcur;
                greatTail=greatTail->next;
            }
            pcur=pcur->next;
        }
        //大链表尾结点置为NULL
        greatTail->next=NULL;
        //大小链表首尾相连
        lessTail->next=greatHead->next;
        ListNode* ret=lessHead->next;
        free(lessHead);
        free(greatHead);
        return ret;
    }
};

1.6 链表的回⽂结构

题目链接

回文结构："abcba"，"12344321"，类似"轴对称"结构

思路一：创建新链表保存原链表所有的结点，反转新链表，比较新旧链表中的结点是否相同

思路二：（投机取巧）创建数组（大小为900），遍历链表将结点的值依次存储在数组中，若数组为回文结构，则链表为回文结构

class PalindromeList
{
    pubilc:
    bool chkPalindrome(ListNode* A)
    {
        int arr[900]={0};//o(900)==o(1)
        //遍历链表，将链表中结点的值依次存储到数组中
        ListNode* pcur=A;//cpp不需要typedef，可以直接用
        while(pcur)
        {
            arr[i++]=pcur->val;
            pcur=pcur->next;
        }
        //判断数组是否为回文结构
        int left=0;
        int right=i-1;
        while(left<right)
        {
            if(arr[left]!=arr[right])
                return false;
            left++;
            right--;
        }
        return true;
    }
}

思路三：找中间结点，将中间结点作为新链表的头结点，反转链表，遍历原链表和反转后链表结点的值是否相等

class PalindromeList
{
    public:
    //找中间结点
   ListNode* middleNode(struct ListNode* head)
   {
       //创建快慢指针
       ListNode* slow=head;
       ListNode*fast=head;
       while(fast!=NULL&&fast->next!=NULL)
       {
           slow=slow->next;
           fast=fast->next->next;
       }
       return slow;
   }
    //反转链表
ListNode* reverseList(struct ListNode* head)
{
    if(head==NULL)
        return head;
    ListNode* n1,*n2,*n3;
    n1=NULL;
    n2=head;
    n3=n2->next;
    while(n2)//以n2为判断条件，不能以n3为判断条件，因为最后n2的下一个要为NULL，如果n3为判断条件，n2最后不会被赋值
    {
        n2->next=n1;
        n1=n2;
        n2=n3;
        if(n3)
        	n3=n3->next;
    }
    return n1;//链表的新的头结点
}
    bool chkPalindrome(ListNode* A)
    {
        //找中间结点
        ListNode* mid=middleNode(A);
        //反转以中间结点为头的链表
        ListNode* right=reverseList(mid);
        //遍历原链表和反转后的链表，比较结点的值是否相等
        ListNode* left=A;
        while(right)
        {
            if(left->val!=right->val)
                return false;
            left=left->next;
            right=right->next;
        }
        return true;
    }
};

1.7 相交链表

题目链接

思路：求两个链表的长度，长链表先走长度差步，长短链表开始同步遍历，找相同的结点

typedef struct ListNode ListNode;
struct ListNode* getIntersectionNode(struct ListNode* headA,struct ListNode* headB)
{
    ListNode* pa=HeadA;
    ListNode* pb=HeadB;
    int sizeA=0,sizeb=0;
    while(pa)
    {
        ++size;
        pa=pa->next;
    }
    while(pb)
    {
        ++size;
        pb=pb->next;
    }
    //求长度差
    int gap=abs(sizeA-sizeB);//求绝对值
    //谁是长链表
    ListNode* shortlist=headA;//先让A链表为短
    ListNode* longList=headB;
    //指针减指针也可以求距离，但是不好判断谁是长链表
    if(sizeA>sizeB)//如果A长，则修改A为长链表
    {
        longList=headA;
        shortList=headB;
    }
    //让长链表先走gap
    while(gap--)
    {
        longList=longList->next;
    }
    //此时长短链表在同一起跑线
    while(shortList)//或者while(longList)
    {
        if(shortList==longList)
        {
            return shortList;//也可以返回longList
        }
        shortList=shortList->next;
        longList=longList->next;
    }
    //链表不相交
    return NULL;
}

相交：

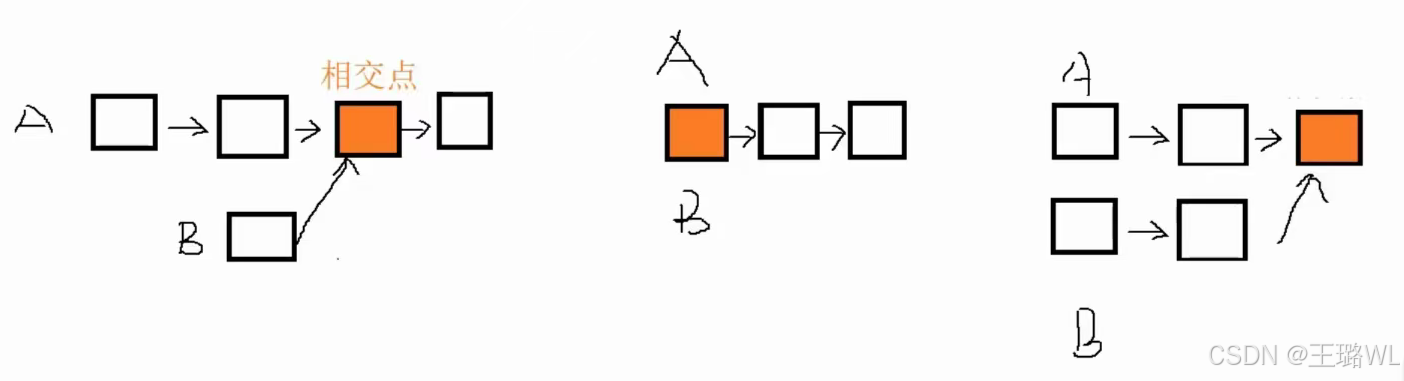
不相交：

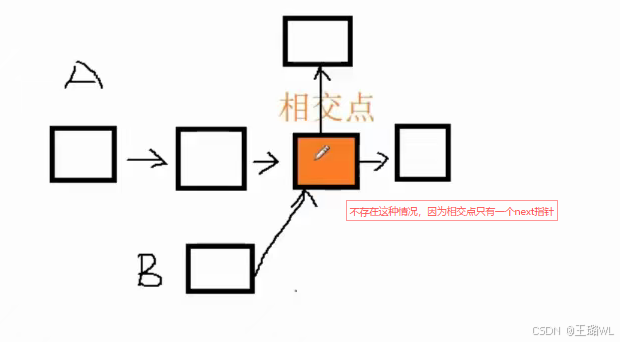
1.8 环形链表I

题目链接

思路：快慢指针，慢指针每次走一步，快指针每次走两步，如果slow和fast指向同一个结点，则链表带环

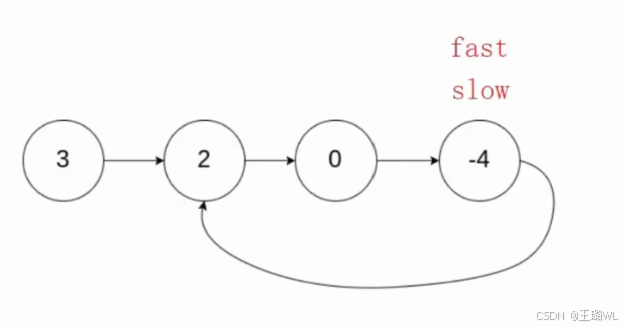
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode* head)
{
    //创建快慢指针
    ListNode* slow=head;
    ListNode* fast=head;
    while(fast&&fast->next)//如果不带环，fast(偶数个)&&fast->next(奇数个)会为空，只要为空，跳出循环返回false
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)
            return ture;
    }
    //链表不带环
    return false;
}

思考1：为什么快指针每次⾛两步，慢指针⾛⼀步可以相遇，有没有可能遇不上，请推理证明！

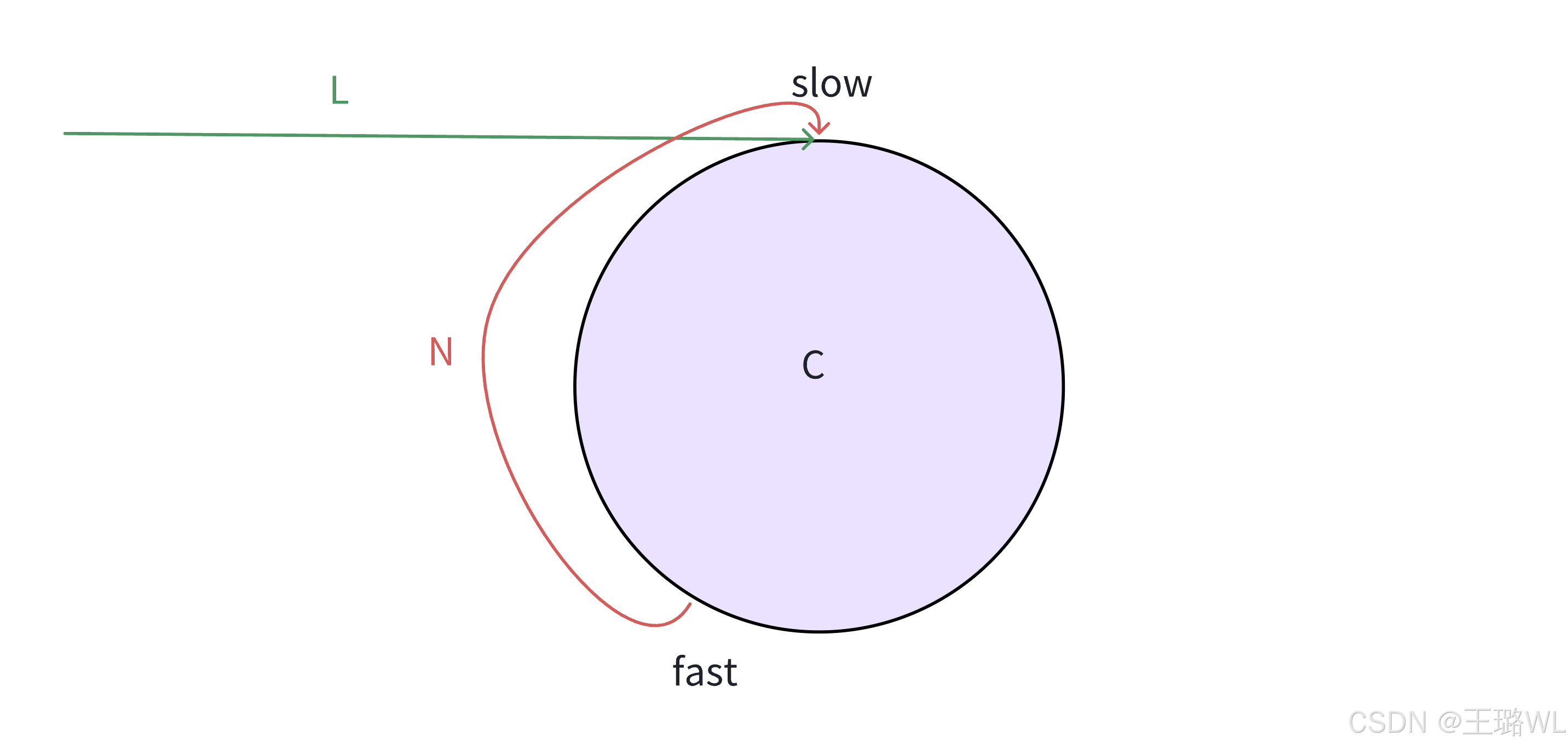
slow⼀次⾛⼀步，fast⼀次⾛2步，fast先进环，

假设slow也⾛完⼊环前的距离，准备进环，此时fast 和slow之间的距离最大为N，

接下来的追逐过程中，每追击⼀次，他们之间的距离缩⼩1步

追击过程中fast和slow之间的距离变化：

因此，在带环链表中慢指针⾛⼀步，快指针⾛两步最终⼀定会相遇。

思考2：快指针⼀次⾛3步，⾛4步，...n步⾏吗?

step1: 按照上⾯的分析，慢指针每次⾛⼀步，快指针每次⾛三步，此时快慢指针的最⼤距离为N，

接下来的追逐过程中，每追击⼀次，他们之间的距离缩⼩2步

追击过程中fast和slow之间的距离变化：

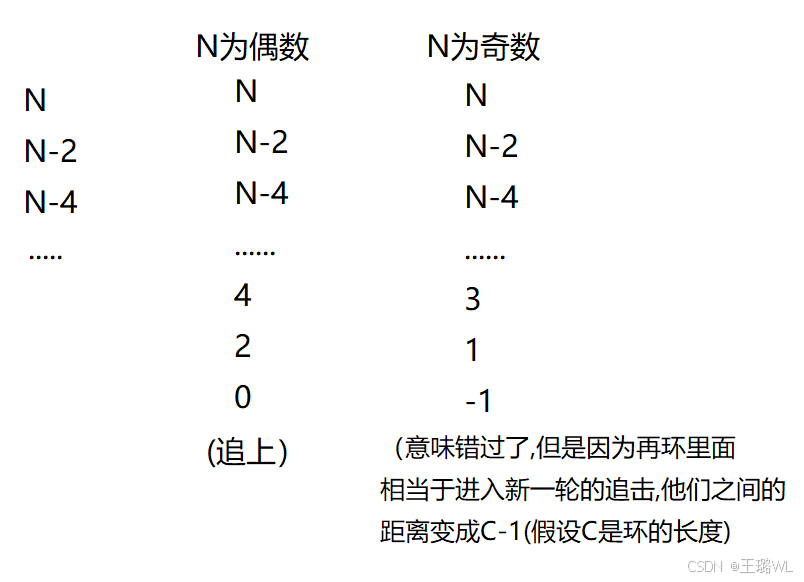
分析: 1、如果N是偶数，会相遇

2、如果N是奇数，第⼀轮追不上，快追上，错过了，距离变成-1，即C-1，进⼊新的⼀轮追击

a、C-1如果是偶数，那么下⼀轮就追上了

b、C-1如果是奇数， 那么就永远都追不上

总结⼀下追不上的前提条件： N是奇数，C是偶数

step2：

假设： 环的周⻓为C，头结点到slow结点的⻓度为L，slow⾛⼀步，fast⾛三步，当slow指针⼊环后， slow和fast指针在环中开始进⾏追逐，假设此时fast指针已经绕环x周。

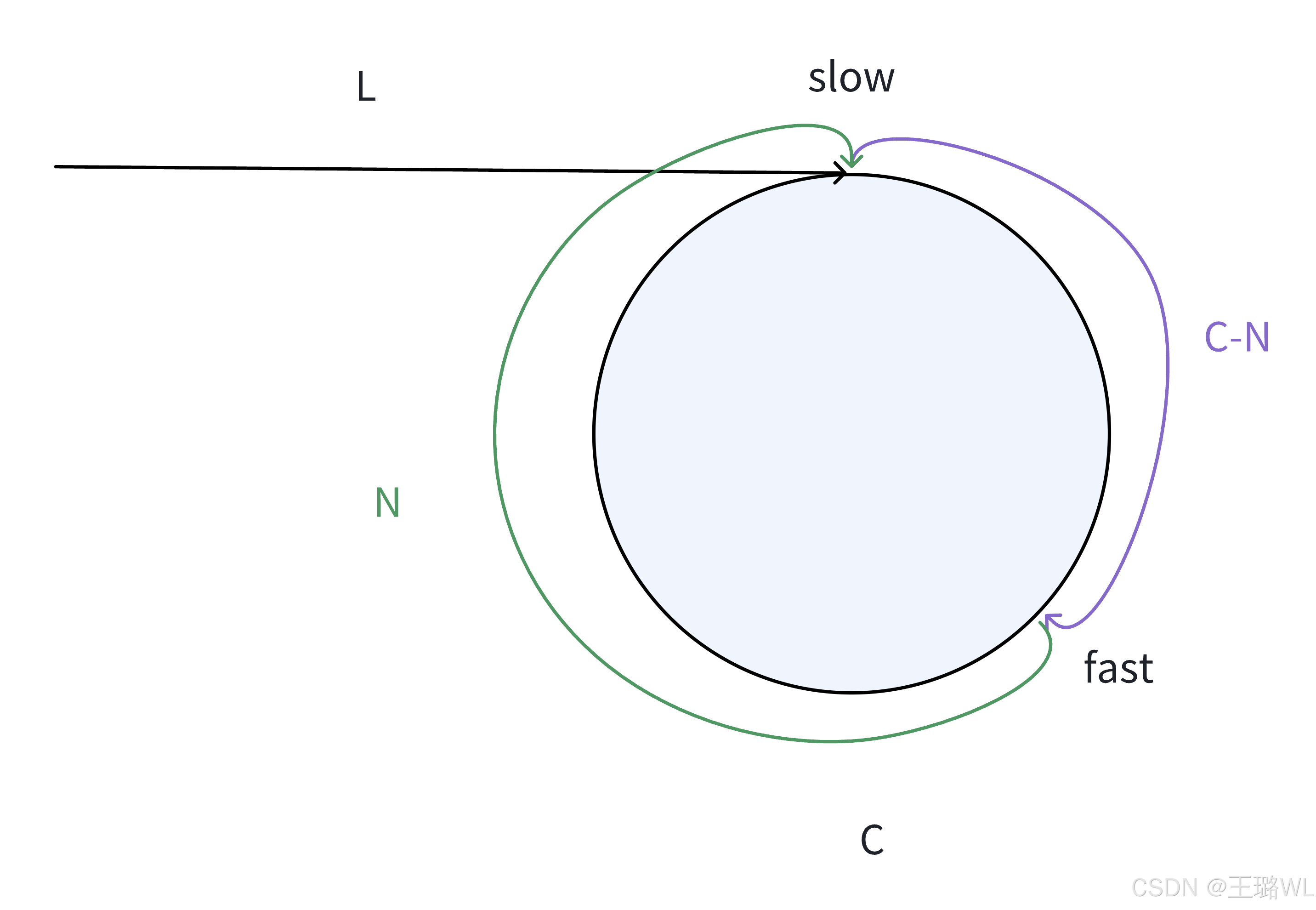
在追逐过程中，快慢指针相遇时所⾛的路径⻓度:

fast: L+xC+C-N

slow：L

由于慢指针⾛⼀步，快指针要⾛三步，因此得出： 3 * 慢指针路程 = 快指针路程 ，即： 3L = L + C − N+ xC，所以2L = (x + 1)C − N

对上述公式继续分析：由于偶数乘以任何数都为偶数，因此⼀定为偶数，则可推导出可能得情况： 2L

• 情况1：偶数=偶数-偶数

• 情况2：偶数=奇数-奇数 由step1中（1）得出的结论，如果N是偶数，则第⼀圈快慢指针就相遇了。 由step1中（2）得出的结论，如果N是奇数，则fast指针和slow指针在第⼀轮的时候套圈了，开始进⾏下⼀轮的追逐；当N是奇数，要满⾜以上的公式，x+1和C都必须为奇数，满⾜相遇结论，则快慢指针会相遇

因此，既然不存在N是奇数，C是偶数的情况，则快指针⼀次⾛3步最终⼀定也可以相遇。

快指针⼀次⾛4、5...步最终也会相遇，其证明⽅式同上。

typedef struct ListNode ListNode; 
bool hasCycle(struct ListNode *head) 
{ 
    ListNode* slow,*fast; 
    slow = fast = head; 
    while(fast && fast->next) 
    { 
        slow = slow->next; 
        int n=3; //fast每次⾛三步 
        while(n--)//可能一个循环里不能直接走三步，不能直接修改外部while判断条件 
        { 
            if(fast->next) 
                fast = fast->next; 
            else 
                return false; 
        } 
        if(slow == fast) 
        { 
            return true; 
        } 
    } 
    return false; 
}

提⽰ 虽然已经证明了快指针不论⾛多少步都可以满⾜在带环链表中相遇，但是在编写代码的时候会有额外的步骤引⼊，涉及到快慢指针的算法题中通常习惯使⽤慢指针⾛⼀步快指针⾛两步的⽅式。

1.9 环形链表II

题目链接

思路：相遇点到入环结点的距离==头结点到入环结点的距离

typedef struct ListNode ListNode;
struct NodeList* detectCycle(struct ListNode* head) 
{
 //创建快慢指针
 ListNode* slow=head;
 ListNode* fast=head;
 while(fast&&fast->next)//如果不带环，fast(偶数个)&&fast->next(奇数个)会为空，只要为空，跳出循环返回false
 {
     slow=slow->next;
     fast=fast->next->next;
     if(slow==fast)
     {
         //相遇了，接下来找入环结点
         ListNode* pcur=head;
         //slow和pcur同时走，相遇的位置就是入环结点
         while(pcur!=slow)//用fast也行
         {
             pcur=pcur->next;
             slow=slow->next;
         }
         return pcur;//return slow;
     }
 }
 //链表不带环
 return NULL;
}

那为什么相遇点到入环结点的距离==头结点到入环结点的距离？

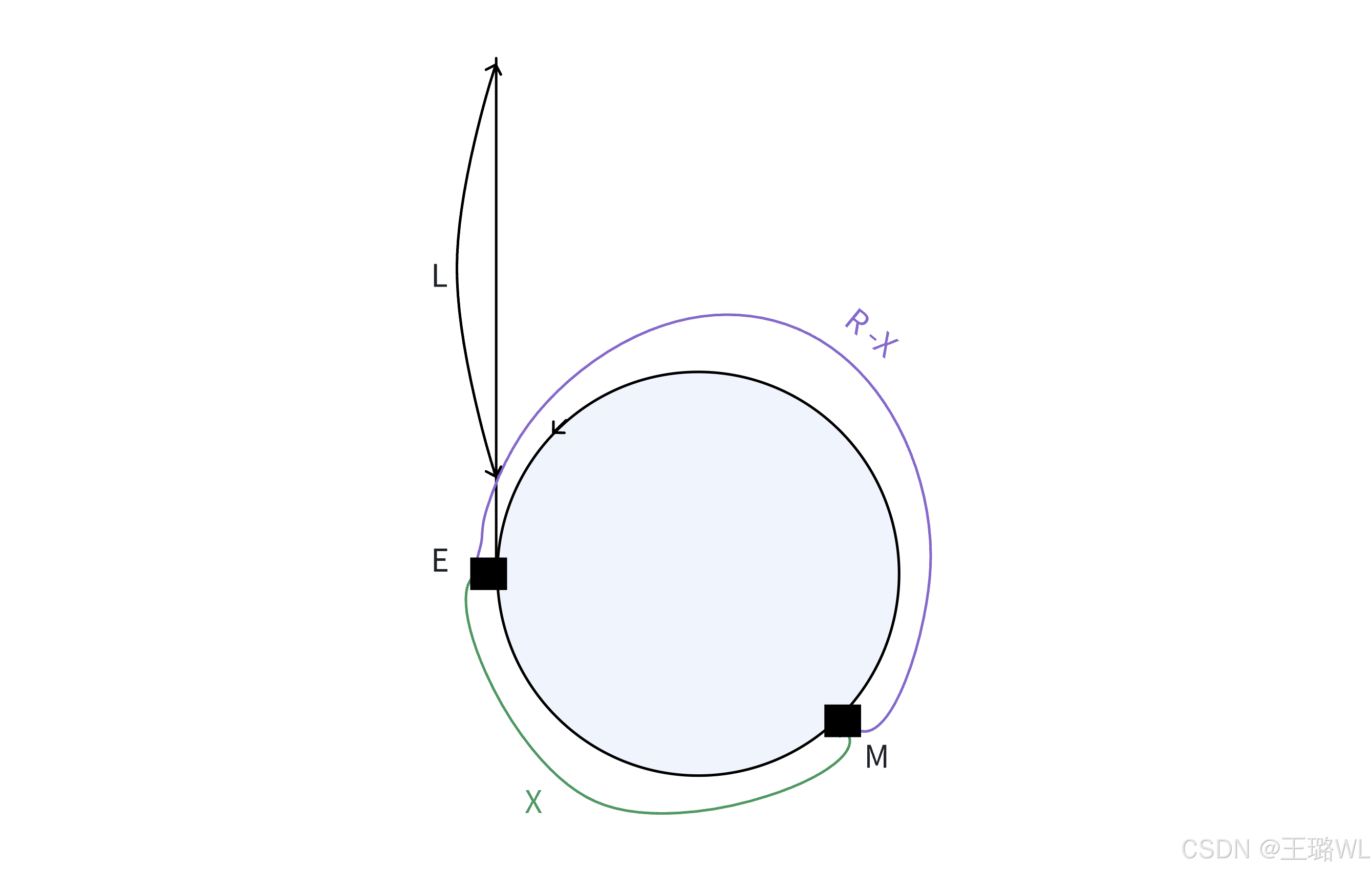
说明: H为链表的起始点，E为环⼊⼝点，M是相遇点

设: 环的⻓度为R，H到E的距离为L，E到M的距离为 X ，则：M到E的距离为 R-X

相遇时，快慢指针相遇时所⾛的路径⻓度: fast: L+X + nR slow：L+X

注意: 1.当慢指针进⼊环时，快指针可能已经在环中绕了n圈了，n⾄少为1

因为快指针先进环⾛到M的位置，最后⼜在M的位置与慢指针相遇

2.慢指针进环之后，快指针肯定会在慢指针⾛⼀圈之内追上慢指针

因为：慢指针进环后，快慢指针之间的距离最多就是环的⻓度，⽽两个指针在移动时，每次它们⾄今的距离都缩减⼀步，因此在慢指针移动⼀圈之前快指针肯定是可以追上慢指针的，⽽快指针速度是满指针的两倍，因此有如下关系是：

2 * (L+X)=L+X+nR

L+X=nR

L=nR-X

L=nR+R-R-X

L = (n-1)R+(R-X) (n为1,2,3,4...，n的⼤⼩取决于环的⼤⼩，环越⼩n越⼤)

L是头结点到入环结点的距离，R-X是相遇点到入环结点的距离，(n-1)R是整圈

极端情况下，假设n=1，此时： L=R-X 即：⼀个指针从链表起始位置运⾏，⼀个指针从相遇点位置绕环，每次都⾛⼀步，两个指针最终会在⼊⼝点的位置相遇

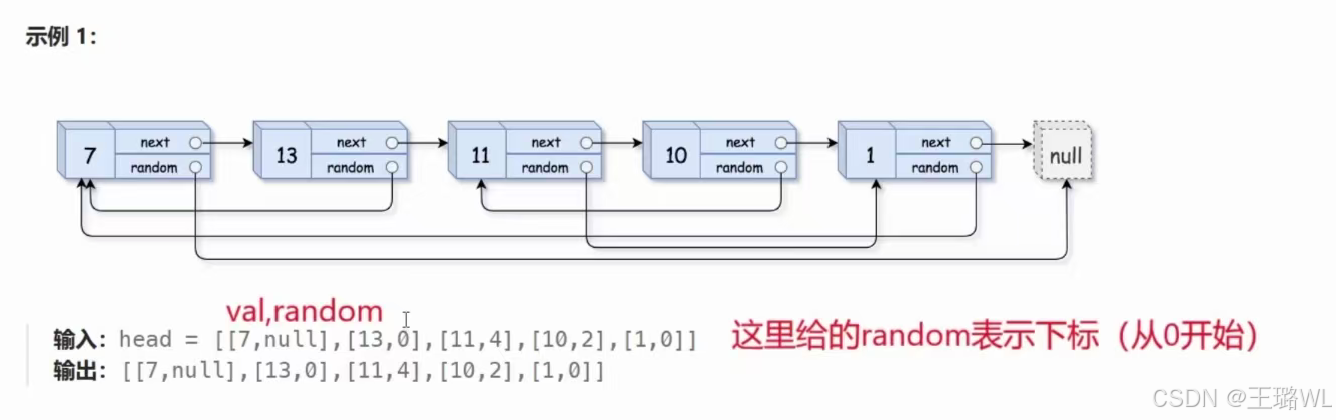
1.10 随机链表的复制

题目链接

深度拷贝 是指在复制对象时，不仅复制对象本身，还递归地复制其所有子对象，从而使新对象与原对象完全独立。与之相对的是浅拷贝，浅拷贝只复制对象的引用，导致新旧对象共享内存。

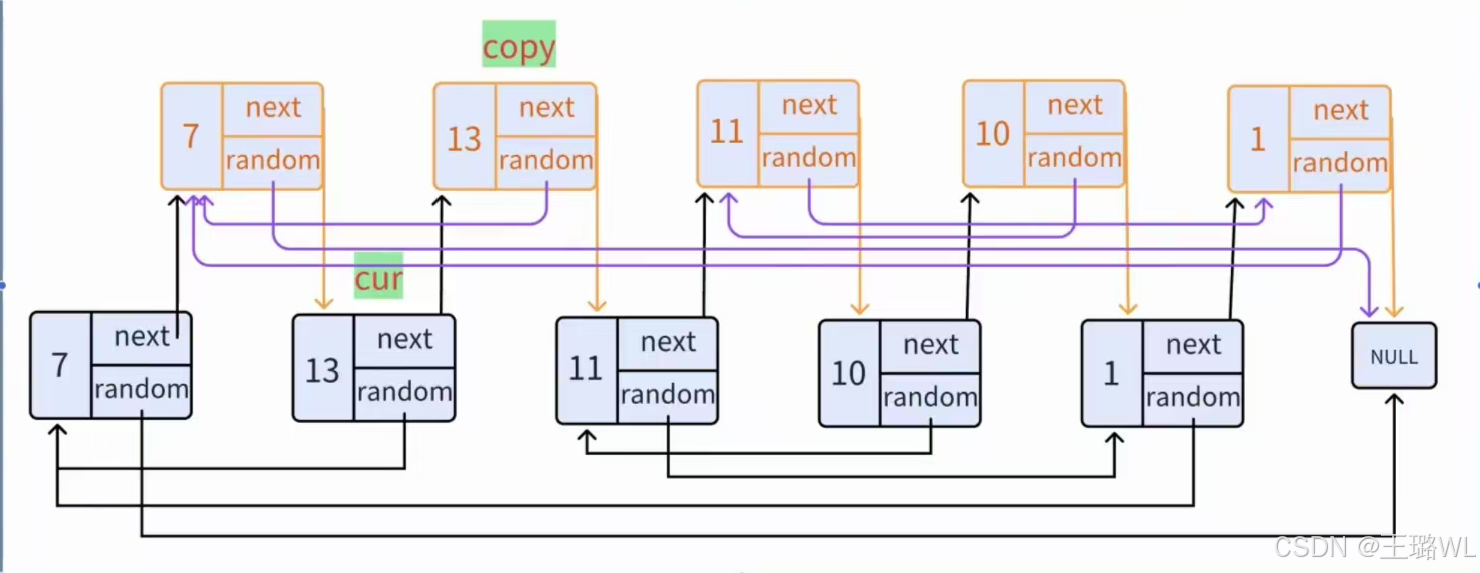
思路：在原有链表基础上拷贝

拷贝random时的思路：如果pcur->random不为空，则拷贝出来的结点的random==pcur->next->random

/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     struct Node *next;
 *     struct Node *random;
 * };
 */
typedef struct Node Node;
//封装一个函数用来创建结点
Node* buyNode(int x)
{
    Node* newnode=(Node*)malloc(sizeof(Node));
    newnode->val=x;
    //先把next和random置为空
    newnode->next=newnode->random=NULL;
	return newnode;
}
//拷贝结点（除random以外的）
void AddNode(Node* head)
{
    Node* pcur=head;
    while(pcur)
    {
        //将pcur的值先拷贝
        Node* newnode=buyNode(pcur->val);
    	//先将原链表pcur下一个结点存起来
        
        Node* next=pcur->next;
        newnode->next=next;
        pcur->next=newnode;
        pcur=next;
        //也可以先连再断
        //newnode->next=pcur->next;
        //pcur->next=newnode;
        //pcur=newnode->next;
    }
    
}
void setRandom(Node* head)
{
    Node* pcur=head;
    while(pcur)
    {
        Node* copy=pcur->next;//现在要修改random
        if(pcur->random)
            copy->random=pcur->random->next;
        pcur=copy->next;//指向原链表的下一个结点
        //else
        //    copy->random=NULL;
        //不需要这两句代码，因为这段代码的意思是
        //pcur->random为空，要给对应新链表的结点的random赋值为NULL，但是新链表的结点的random本来就是NULL
        //不需要再次赋值
    }
}
struct Node* copyRandomList(struct Node* head) 
{
    //如果是空链表
    if(head==NULL)
        return head;
	//1.在原链表基础上拷贝结点并插入原链表中
    AddNode(head);
    //2.设置random
    setRandom(head); 
    //3.与新链表断开
    Node* pcur=head;
    Node* copyHead,copyTail;
    copyHead=copyTail=pcur->next;
    //只要新链表结点的尾结点不为空
    while(copyTail->next)
    {
        pcur=copyTail->next;
        copyTail->next=pcur->next;
        copyTail=copyTail->next;
    }
    return copyHead;
}

更多链表算法刷题⼊⼝：

牛客网

LeetCode