1.AT_arc170_a Yet Another AB Problem
题意

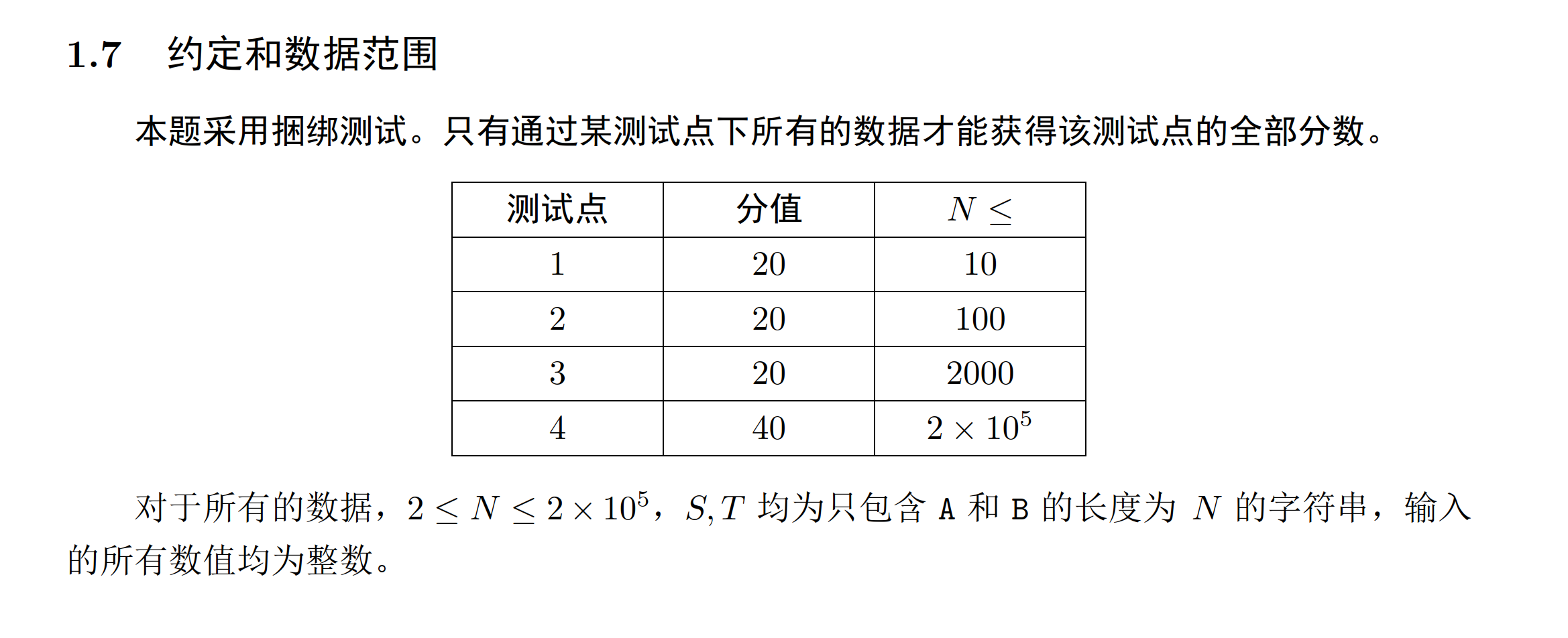
思路
从前往后扫 s s s,记录 s i ≠ t i s_i\neq t_i si=ti 的位置上是 A 还是 B(B 需要变成 A,A 需要变成 B)。如果遇到一个 B 就先记录下来;如果遇到一个 A,就看前面有没有记录过(剩余)B,如果有就可以配成一对,操作一次 A B。
于是最后会剩下一些 A 在前面和一些 B 在后面,那么只要最后一个(要被替换的) B 后面还有 s i = t i s_i=t_i si=ti 的 B,和第一个 A 前面还有 A,就是有解的。
代码1(Atcoder WA on #18)
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2e5+9;
ll n;
char s[N],t[N];
ll pos1[N],pos2[N];
int main()
{
freopen("replace.in","r",stdin);
freopen("replace.out","w",stdout);
scanf("%lld%s%s",&n,s+1,t+1);
ll bta=0;
ll atb=0;
ll ans=0;
for(int i=1;i<=n;i++)
{
if(s[i]!=t[i])
{
if(s[i]=='B')
{
pos1[++bta]=i;
}
else
{
if(bta)
{
s[pos1[bta]]='A',s[i]='B';
ans++;
bta--;
}
else pos2[++atb]=i;
}
}
}
if(atb==0&&bta==0)
{
printf("%lld",ans);
return 0;
}
bool f1=0,f2=0;
for(int i=pos1[bta]+1;i<=n;i++)
if(s[i]=='B')f1=1;
for(int i=1;i<pos2[1];i++)
if(s[i]=='A')f2=1;
if(f1&&f2)
{
printf("%lld",ans+atb+bta);
}
else puts("-1");
return 0;
} 但是这个代码总会被卡 1 ∼ 2 1\sim 2 1∼2 个点呢。于是换了一个写法。
代码2(Atcoder AC)
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2e5+9;
ll n;
char s[N],t[N];
ll pos1[N],pos2[N];
int main()
{
freopen("replace.in","r",stdin);
freopen("replace.out","w",stdout);
scanf("%lld%s%s",&n,s+1,t+1);
for(int i=1;i<=n;i++)
{
if(t[i]=='A')break;
if(s[i]=='A')
{
puts("-1");
return 0;
}
}
for(int i=n;i>=1;i--)
{
if(t[i]=='B')break;
if(s[i]=='B')
{
puts("-1");
return 0;
}
}
ll ans=0;
for(int i=1;i<=n;i++)
ans+=(s[i]!=t[i]);
ll cnt=0;
for(int i=1;i<=n;i++)
{
if(s[i]==t[i])continue;
if(t[i]=='A')cnt++;
if(cnt&&t[i]=='B')ans--,cnt--;
}
printf("%lld",ans);
return 0;
} 2.洛谷 P12966 CCO2025 Asteroid Mining
题意

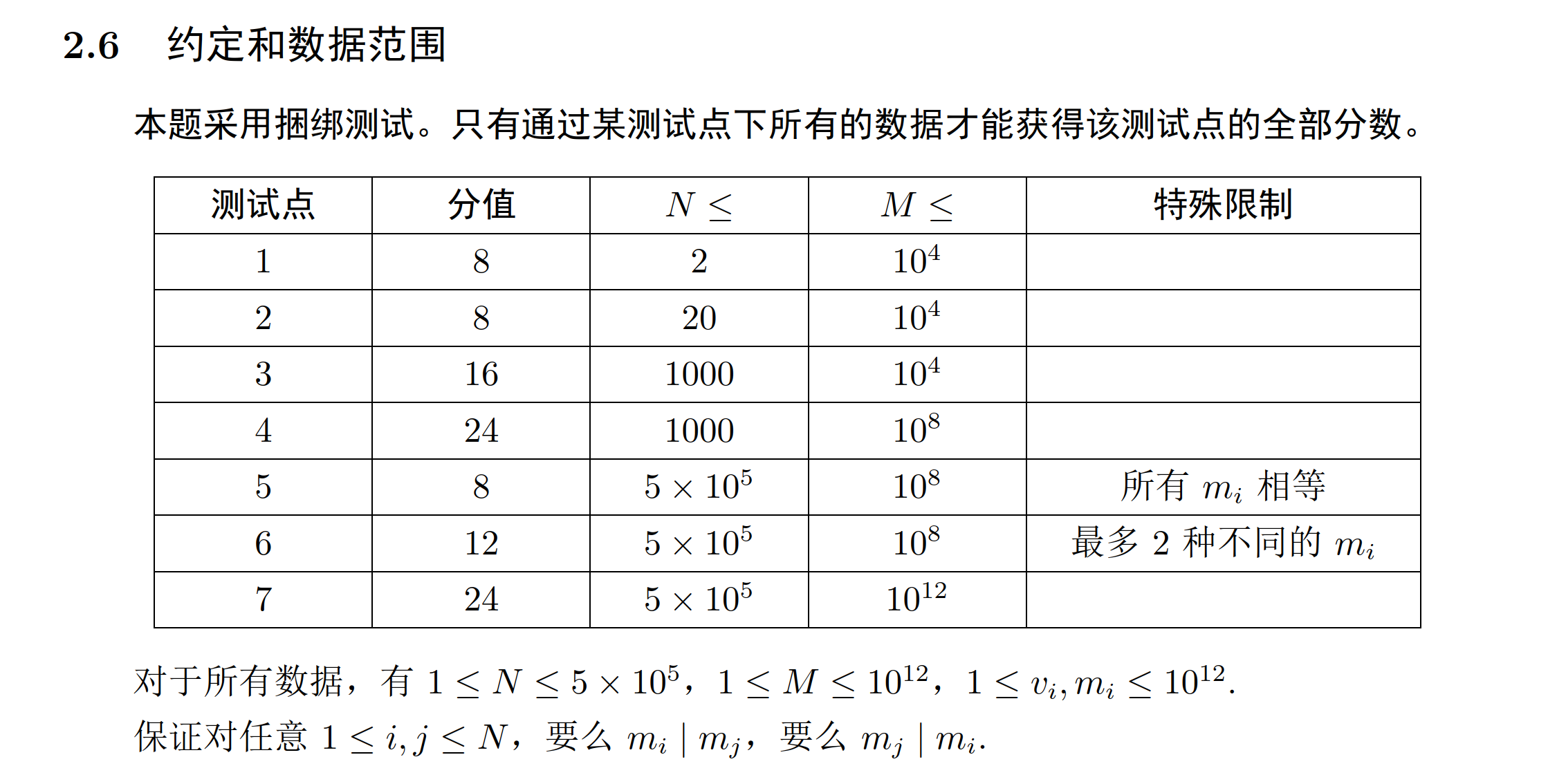
思路
赛时观察到质量种树只有 log M = 40 \log M=40 logM=40 种也没什么头绪,只会拼命敲部分分呢打了 40pts 的 dp 呢。但是感觉 dp 没什么前途------毕竟这个数据给你,就不是用来 dp 的,于是考虑贪心。
按照质量排序,首先 m 1 ∣ m 2 ∼ n m_1|m_{2\sim n} m1∣m2∼n,所以 m 2 ∼ n m_{2\sim n} m2∼n 怎么组合,最后都会剩下 ⌊ M / m 1 ⌋ m o d m 2 \left\lfloor M/m_1\right\rfloor \bmod m_2 ⌊M/m1⌋modm2 的没法选,这部分全部用来选质量为 m 1 m_1 m1 的必然优的。
cpp
ll g=W/ww[i],meg=ww[i+1]/ww[i],vlen=vec[i].size();//当前可以选g个i质量;meg个i可以合成i+1
sort(vec[i].begin(),vec[i].end(),cmp2);//贪心选多的
ll pre=min(vlen,(i==nn?g:g%meg));//g%meg个给后面也选不了,强制给i
ll pos=0;
for(;pos<pre;pos++)
{
ans+=vec[i][pos];
W--;
}
if(i==nn)break;那么质量为 m 1 m_1 m1 的还有剩余怎么办?有一个精妙的解决方法,就是把上面代码的 m e g meg meg 个 m 1 m_1 m1 合成一个 m 2 m_2 m2 质量的大块。
如果有合不到 m 2 m_2 m2 的怎么办呢?其实没有关系,假设最后一块没合完的为 m x m_x mx,因为 m 2 m_2 m2 成为当前最小时, ⌊ M ′ / m 2 ⌋ m o d m 3 \left\lfloor M'/m_2\right\rfloor \bmod m_3 ⌊M′/m2⌋modm3 的余量,不会因为 m x < m 2 m_x<m_2 mx<m2 而装不下 m x m_x mx,于是是没有影响的。
代码
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=5e5+9;
ll n,W;
struct node
{
ll v,w;
}a[N];
bool cmp(node x,node y)
{
return x.w<y.w;
}
bool cmp2(ll x,ll y)
{
return x>y;
}
ll ww[N],nn;
vector<ll>vec[N];
int main()
{
freopen("mining.in","r",stdin);
freopen("mining.out","w",stdout);
scanf("%lld%lld",&n,&W);
for(int i=1;i<=n;i++)
{
ll v,w;
scanf("%lld%lld",&v,&w);
a[i]=(node){v,w};
ww[i]=w;
}
sort(a+1,a+n+1,cmp);
ww[0]=1;
for(int i=1;i<=n;i++)
{
if(a[i].w!=a[i-1].w)nn++;
vec[nn].push_back(a[i].v);
ww[nn]=a[i].w;
}
ll ans=0;
for(int i=1;i<=nn;i++)
{
ll g=W/ww[i],meg=ww[i+1]/ww[i],vlen=vec[i].size();//当前可以选g个i质量;meg个i可以合成i+1
sort(vec[i].begin(),vec[i].end(),cmp2);
ll pre=min(vlen,(i==nn?g:g%meg));//g%meg个给后面也选不了,强制给i
ll pos=0;
for(;pos<pre;pos++)
{
ans+=vec[i][pos];
W--;
}
if(i==nn)break;
for(;pos<vlen;)
{
ll meg_sum=0;
for(int k=1;k<=meg&&pos<vlen;k++)//如果合成不到质量为ww[i+1]的就不管了
{
meg_sum+=vec[i][pos];
pos++;
}
vec[i+1].push_back(meg_sum);
}
}
printf("%lld",ans);
return 0;
}3.洛谷 P12914 POI2020 沙滩游客 / Plażowicze
题意

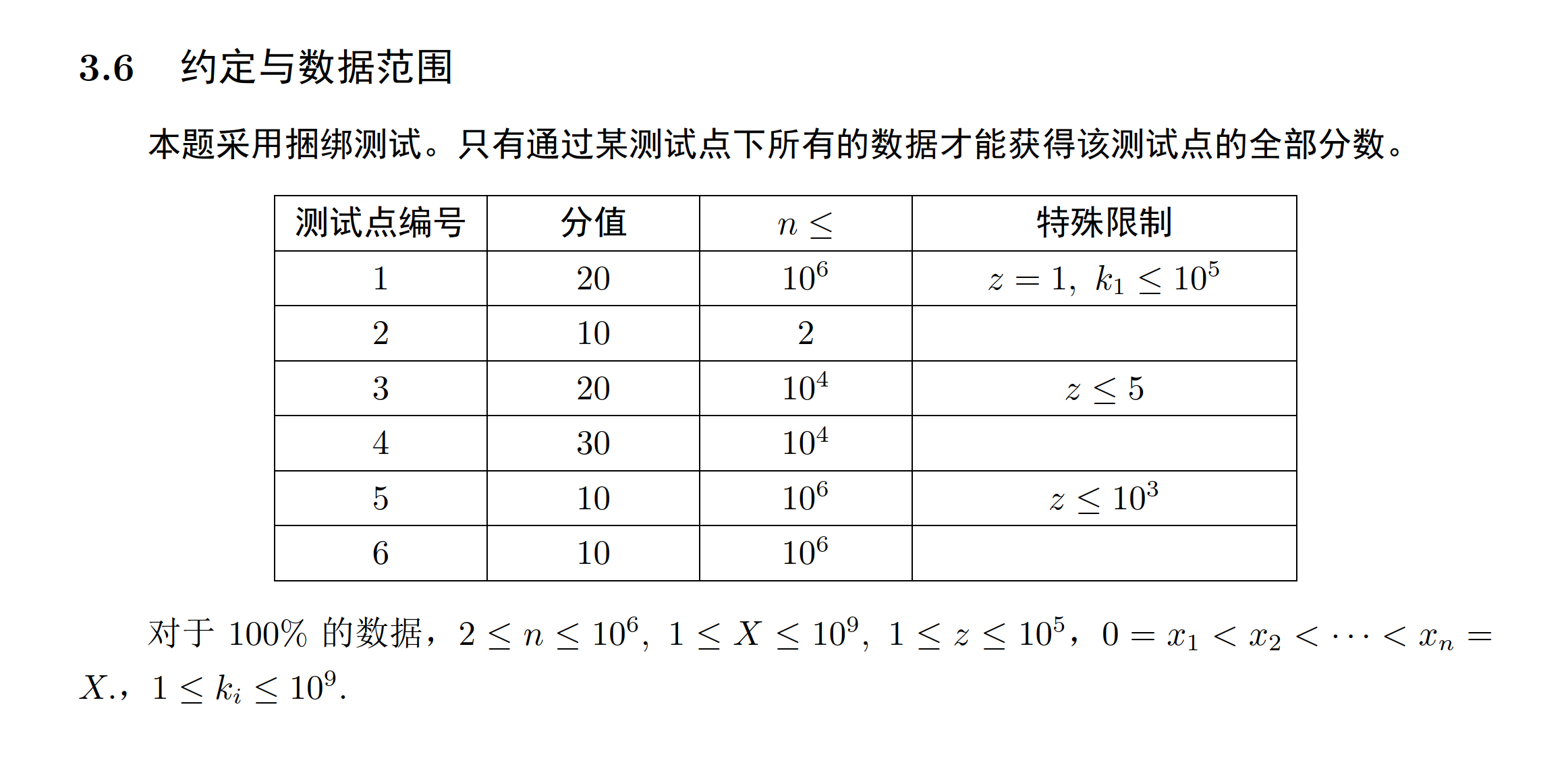
思路
赛时写了一个维护所有区间的大堆和分数的各种 operator,借用 O3 神力卡到 50pts。就是每次选一个长度最长的,尽量靠左的区间,位置选在中间,然后把该区间对半劈开。堆维护区间长度和左右端点。
但是正解其实就是暴力的一点小优化。因为劈开一次会多一个,所以 k ≤ 1 0 9 k\le 10^9 k≤109 的询问就会多 1 0 9 10^9 109 个。我们不想塞那么多东西到堆里。并且随着分裂次数增大,堆顶会有一堆长度相等的最大长度。
所以直接维护 3 3 3 个东西:分裂开的区间长度、原来的左端点和分裂的元素个数(右端点可不维护)。这样堆里始终只有 n n n 个元素,而 n n n 个元素里面劈开的小区间长度都相同,于是按照分裂区间长度为秩是正确的。根据新增分裂段数更新答案即可。时间复杂度 O ( min ( n log n , q ) ) O(\min(n\log n,q)) O(min(nlogn,q))。
代码
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline ll read()
{
ll s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
inline void write(ll x)
{
if(x==0){putchar('0');return;}
ll len=0,k1=x,c[10005];
if(k1<0)k1=-k1,putchar('-');
while(k1)c[len++]=k1%10+'0',k1/=10;
while(len--)putchar(c[len]);
}
const ll N=1e6+9;
ll n,R,m;
ll a[N];
//-------↓分数类 -------
struct Fs
{
ll fz,fm;
void print()
{
ll g=__gcd(fz,fm);
fz/=g,fm/=g;
write(fz);
printf("/");
write(fm);
puts("");
}
};
inline Fs yf(Fs x)
{
Fs z=x;
ll g=__gcd(z.fz,z.fm);
z.fz/=g,z.fm/=g;
return z;
}
inline Fs operator + (Fs x,Fs y)
{
Fs z={0,0};
z.fm=max(x.fm,y.fm);
z.fz=z.fm/x.fm*x.fz+z.fm/y.fm*y.fz;
return z;
}
inline Fs operator * (Fs x,ll k)
{
Fs z=x;
z.fz*=k;
return z;
}
inline Fs operator / (Fs x,ll k)
{
Fs z=x;
z.fm*=k;
return z;
}
inline bool operator == (Fs x,Fs y)
{
return x.fz*y.fm==y.fz*x.fm;
}
inline bool operator < (Fs x,Fs y)
{
return x.fz*y.fm<y.fz*x.fm;
}
inline bool operator > (Fs x,Fs y)
{
return x.fz*y.fm>y.fz*x.fm;
}
//-------↑分数类 -------
struct que
{
ll k,id;
}Q[N];
inline bool cmp(que x,que y)
{
return x.k<y.k;
}
struct node
{
Fs l,r,Dis;
ll cnt;
};
inline bool operator < (node x,node y)
{
if(x.Dis==y.Dis)return x.l>y.l;
return x.Dis<y.Dis;
}
priority_queue<node>q;
Fs ANS[N];
int main()
{
// freopen("beach23.in","r",stdin);
// freopen("beach.out","w",stdout);
n=read(),R=read(),m=read();
for(int i=1;i<=n;i++)
{
a[i]=read();
if(i>1)q.push((node){(Fs){a[i-1],1},(Fs){a[i],1},(Fs){a[i]-a[i-1],1},1});
}
for(int i=1;i<=m;i++)
{
ll k=read();
Q[i]=(que){k,i};
}
sort(Q+1,Q+m+1,cmp);
ll tick=0,pos=1;
while(1)//tick分裂次数
{
node tem=q.top();
q.pop();
ll l=tick+1,r;
tick+=tem.cnt;
r=tick;
//加一轮/2的贡献,l分裂前r分裂后
while(pos<=m&&Q[pos].k<=r)
{
Fs Mid=(tem.l+tem.Dis*(Q[pos].k-l))+tem.Dis/2;
ANS[Q[pos].id]=yf(Mid);
pos++;
}
tem.Dis=tem.Dis/2;
tem.cnt*=2;
q.push(tem);
if(pos>m||tick>=Q[m].k)break;
}
for(int i=1;i<=m;i++)
ANS[i].print();
return 0;
}4.洛谷 P8169 eJOI2021 Dungeons
先看着大佬的博客,待补。