递归的应用
- 导读
- [一、50. `Pow(x, n)`------快速幂](#一、50.
Pow(x, n)——快速幂) -
- [1.1 题目介绍](#1.1 题目介绍)
- [1.2 解题思路](#1.2 解题思路)
- [1.3 编写代码](#1.3 编写代码)
-
- [1.3.1 定义函数](#1.3.1 定义函数)
- [1.3.2 寻找递归基](#1.3.2 寻找递归基)
- [1.3.3 寻找递进关系](#1.3.3 寻找递进关系)
- [1.3.4 组合优化](#1.3.4 组合优化)
- [1.4 代码测试](#1.4 代码测试)
- 结语

导读
大家好,很高兴又和大家见面啦!!!
在上一篇内容中,我们通过经典的汉诺塔问题 深入探讨了递归算法的核心思想。汉诺塔问题完美展示了如何将复杂问题分解为相似的子问题,通过递归调用优雅解决 。这种"分而治之"的思维不仅是理解递归的关键,更是算法设计的精髓所在。
今天,我们将继续递归的探索之旅,但这次我们的战场转向了一个看似简单却暗藏玄机的问题------如何高效计算幂运算。
当我们面对LeetCode第50题《Pow(x, n)》时,朴素的迭代方法在指数范围达到 − 2 31 ≤ n ≤ 2 31 − 1 -2^{31} \leq n \leq 2^{31} - 1 −231≤n≤231−1 时会显得力不从心。
但正如汉诺塔问题教会我们的,递归的魅力在于它能将复杂问题化繁为简。让我们一同看看,递归思维如何将幂运算的时间复杂度从 O ( n ) O(n) O(n) 优化到 O ( log n ) O(\log n) O(logn),体验算法优化带来的思维飞跃!
一、50. Pow(x, n)------快速幂
1.1 题目介绍
相关标签 :递归、数学
题目难度 :中等
题目描述 :
实现 pow(x, n) ,即计算 x x x 的整数 n n n 次幂函数(即, x n x^n xn )。
示例 1 :
输入:x = 2.00000, n = 10
输出:1024.00000
示例 2 :
输入:x = 2.10000, n = 3
输出:9.26100
示例 3 :
输入:x = 2.00000, n = -2
输出:0.25000
解释:2 - 2 = 1 / 22 = 1 / 4 = 0.25
提示:
- 00.0 < x < 100.0 00.0 < x < 100.0 00.0<x<100.0
- − 2 31 ≤ n ≤ 2 31 − 1 -2^{31} \leq n \leq 2^{31} - 1 −231≤n≤231−1
- n n n 是一个整数
- 要么 x x x 不为零,要么 n > 0 n > 0 n>0 。
- 1 0 4 ≤ x n ≤ 1 0 4 10^4 \leq x^n \leq 10^4 104≤xn≤104
1.2 解题思路
库函数 pow(x, n)是用于求取 x n x^n xn ,现在我们要实现这么一个库函数,最简单的方法就是------迭代:
c
double Pow(int x, int n) {
double ans = 1.0;
for (int i = 0; i < n; i++) {
ans *= x;
}
return ans;
}但是如果直接使用该代码,在 − 2 31 ≤ n ≤ 2 31 − 1 -2^{31} \leq n \leq 2^{31} - 1 −231≤n≤231−1 该范围下,代码是 100 % 100\% 100% 超时的。
因此为了更好的解决该问题规模下的 Pow(x, n) 的模拟实现,这里我们需要学习一个算法------快速幂;
快速幂 (Exponentiation by Squaring )是一种高效计算幂运算的算法 ,特别适用于计算大整数幂(如 a n a^n an )的情况。
它的核心思想 是将指数进行二进制分解,通过不断平方和乘法来减少计算次数 ,将时间复杂度从朴素的 O ( n ) O(n) O(n) 优化到 O ( log n ) O(\log n) O(logn)。
简单的理解就是当我们要计算 x n x^n xn ,我们就需要将其转化为求 x i ∗ x j x^i * x^j xi∗xj ,其中 n , i , j n, i, j n,i,j 这三者之间的关系为:
- 当 n n n 为偶数时, i = = j i == j i==j
- 当 n n n 为奇数时, j = = i + 1 j == i + 1 j==i+1
我们在整个计算的过程中,通过不断的将指数 n n n 进行二分,来达到快速求解的目的。
就比如我们要计算 2 8 2^8 28 ,其对应的递归树为:
2^8 2^4 2^4 2^2 2^2 2^1 2^1
整个过程中,我们实际上需要计算的 4 4 4 次,即可求出最终的结果;
但是如果我们要采用迭代的方式实现的话,我们则需要执行 8 8 8 次 ∗ 2 *2 ∗2;
若指数 n n n 为奇数,我们则可以将其转化为: x i ∗ x i ∗ x x^i * x^i * x xi∗xi∗x,也就是说,我们每次进行分解的都是偶次幂,而对应的奇次幂,我们只需要在获取的偶次幂的结果的基础上再乘上一个 x x x 即可解决;
如我们要就算 2 1 7 2^17 217 ,其对应的递归树为:
2^17 2^8 2^9 =
2^8 * 2 2^4 2^4 2^2 2^2 2^1 2^1
接下来我们就来实现这一过程;
1.3 编写代码
1.3.1 定义函数
在 pow 这个库函数中,只存在两个参数:
int x:需要求解的底数 x x xint n:需要求解的指数 n n n
函数的返回值应该是一个 double 指,因此对应的函数定义为:
c
double Pow(int x, int n) {
}1.3.2 寻找递归基
在数的幂运算中,下面几个值是不需要进行外计算,便可直接得出结果:
- x 1 = = x x ^ 1 == x x1==x
- x 0 = = 1 x ^ 0 == 1 x0==1
- x − 1 = = 1 x x ^{-1} == \frac{1}{x} x−1==x1
因此我们可以将这三个值作为函数的递归基:
c
if (n == -1) {
return 1 / x;
}
if (n == 0) {
return 1;
}
if (n == 1) {
return x;
}当然我们也可以将 ±2 也作为函数基,这里就看个人的选择;
1.3.3 寻找递进关系
在快速幂中,函数的每次递进都是以 n / 2 n / 2 n/2 的方式进行,即快速幂的递推公式为:
- 当 n n % 2 == 0 n 时, x n = x n 2 ∗ x n 2 x^n = x^{\frac{n}{2}} * x^{\frac{n}{2}} xn=x2n∗x2n
- 当 n n % 2 == 1 n 时, x n = x n 2 ∗ x n 2 ∗ x x^n = x^{\frac{n}{2}} * x^{\frac{n}{2}} * x xn=x2n∗x2n∗x
对应的递归代码为:
c
double tmp = Pow(x, n / 2);
if (n % 2 == 0) {
return tmp * tmp;
}
return tmp * tmp * x;1.3.4 组合优化
现在我们就已经完成了代码的初步框架:
c
double Pow(int x, int n) {
if (n == -1) {
return 1 / x;
}
if (n == 0) {
return 1;
}
if (n == 1) {
return x;
}
double tmp = Pow(x, n / 2);
if (n % 2 == 0) {
return tmp * tmp;
}
return tmp * tmp * x;
}但此时的代码并不完整,我们还需要处理 n < 0 n < 0 n<0 的情况;
特殊情况处理
当 n < 0 n < 0 n<0 时,我们在计算 x n x^n xn 时,实际上就算的是 1 x − n \frac{1}{x^{-n}} x−n1,因此我们不如直接在进行幂运算之前,直接预先处理 n < 0 n < 0 n<0 的情况:
c
if (n < 0) {
x = 1 / x;
n = -n;
}但是如果直接这样处理,那么当 n = = − 2 31 n == -2^{31} n==−231 时,经过该处理后,此时 n = = 2 31 n == 2 ^{31} n==231 ,这时就会出现整型溢出的情况;
那如何避免这个问题呢?
这里有一个小技巧,我们可以通过进行强制类型转换来将 int 强制转换为 long long ;
当然,在此题中,我们可以将我们写的递归函数与 leetcode 中给定的接口分开,并且在调用 Pow(x, n) 之前,我们直接通过变量 long long exp 来接收参数 n 的值,之后再对 exp 进行预处理,最后再进行函数调用:
c
double myPow(double x, int n) {
long long exp = n;
if (n < 0) {
x = 1 / x;
exp *= -1;
}
return Pow(x, exp);
}当经过该预处理后,在 Pow(x, n) 的调用中,指数 n 一定大于 0 ,因此我们就可以去掉递归基:
c
if (n == -1) {
return 1 / x;
}参数优化
从题目给定的函数接口我们可以看到,原参数 x 的类型为 double 类型,因此我们所写的函数参数类型也应该与之同步,即,将 int 修改为 double,完整代码如下:
c
double Pow(double x, long long n) {
if (n == 0) {
return 1;
}
if (n == 1) {
return x;
}
double tmp = Pow(x, n / 2);
if (n % 2 == 0) {
return tmp * tmp;
}
return tmp * tmp * x;
}
double myPow(double x, int n) {
long long exp = n;
if (n < 0) {
x = 1 / x;
exp *= -1;
}
return Pow(x, exp);
}1.4 代码测试
下面我们就在 leetcode 中测试一下对应的代码:
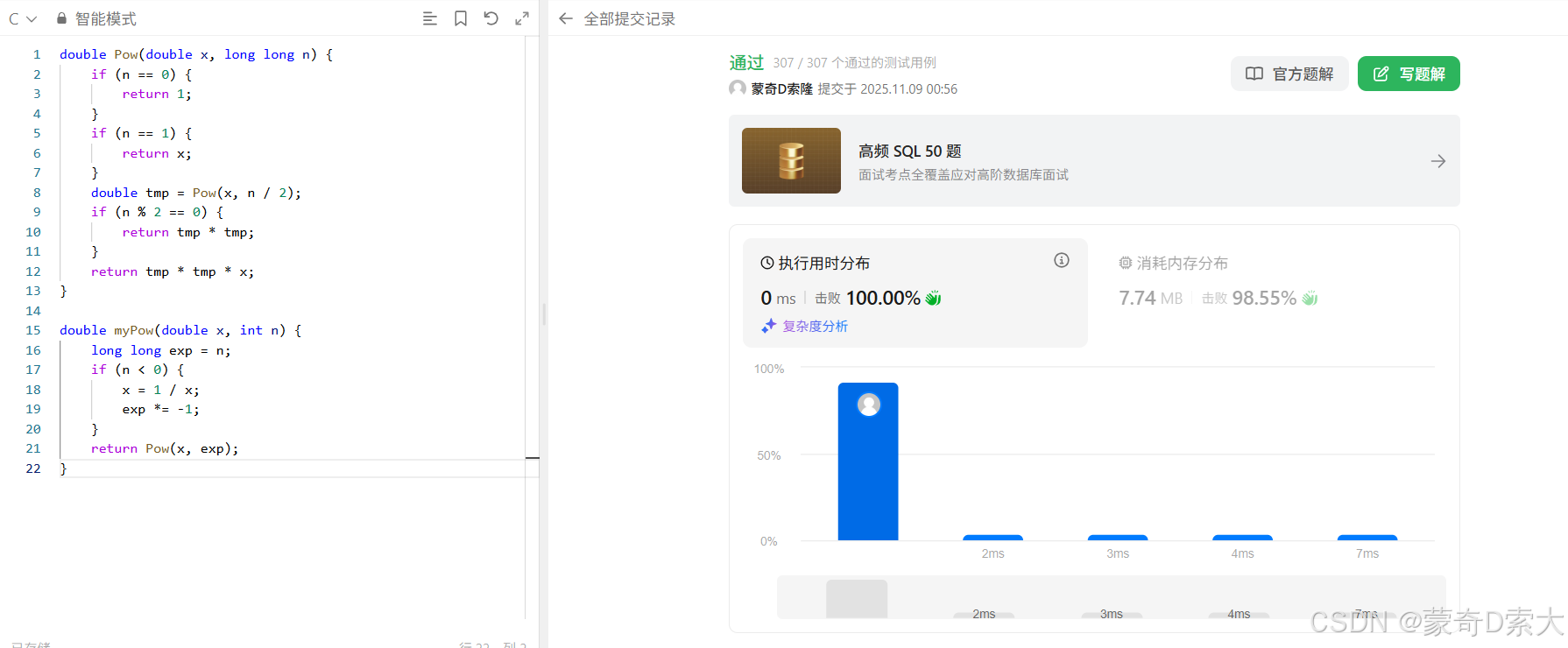
此时我们就已经实现了 快速幂 的算法实现。这里有朋友可能会说,你这都已经定义了 n == 0 为递归基,那是否就不需要 n == 1 作为递归基了?
这个问题的答案是,可以省略 n == 1 作为递归基,但是我这里加上是为了减少一次递归调用,即当 n > 0 n > 0 n>0 时,函数只需要递进到 n == 1 即可结束;
如果省略了该递归基,那么函数则需要递进到 n == 0 才能结束;
当然,具体是只使用 n == 0 作为递归基,还是同时使用 n == 0 和 n == 1 作为递归基,就看个人的编码习惯了;
结语
通过今天对快速幂算法的深入探讨,我们再次见证了递归思维在解决复杂问题时的强大威力。从汉诺塔问题的分治思想 ,到快速幂的二分策略 ,递归始终贯穿着"化繁为简"的核心哲学。
快速幂算法 不仅是一个高效的数学工具,更是算法优化思维的完美体现。它教会我们,在面对看似简单的问题时,深入思考其内在规律往往能带来数量级的性能提升。从朴素的 O ( n ) O(n) O(n) 迭代到精妙的 O ( log n ) O(\log n) O(logn)递归,这种思维跃迁正是算法学习的精髓所在。
更重要的是,我们在实现过程中考虑的边界情况处理 、整数溢出防范等细节,体现了工程实践中不可或缺的严谨态度。这些经验对于解决实际开发中的复杂问题具有重要的借鉴意义。
递归的世界远不止于此,在接下来的内容中,我们将继续探索递归在更多经典问题中的应用,如二叉树的遍历 、回溯算法等,进一步深化对这种强大编程范式的理解。
下篇预告:递归在数据结构中的应用------二叉树的深度优先遍历
互动与分享
-
点赞👍 - 您的认可是我持续创作的最大动力
-
收藏⭐ - 方便随时回顾这些重要的基础概念
-
转发↗️ - 分享给更多可能需要的朋友
-
评论💬 - 欢迎留下您的宝贵意见或想讨论的话题
感谢您的耐心阅读! 关注博主,不错过更多技术干货。我们下一篇再见!