KKT条件：对偶问题、KKT条件以及内点法

整理自YouTube视频：

本文主要分为三个部分：

一个实际的优化问题，用来引出对偶问题
对偶问题的定义
KKT条件
内点法

一个实际的优化问题

鸽闷现在泡在一个半径为1的圆形浴池里，浴池的范围为x2+y2≤1x^2+y^2\leq 1x2+y2≤1。鸽闷的坐标为(x,y)(x, y)(x,y)。

突然在浴池的右上方c=(12,12)c = (\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})c=(2 1,2 1)处开始放开水，鸽闷怕被烫着所以需要寻找一个凉快地方，同时又不想出池子。我希望尽量离ccc点远点。用内积来描述我和c点的远近程度，内积越小，我离c点越远。

于是这个事情等价于一个优化问题：

min⁡x1,x2x1+x2s.t. x12+x22−1≤0\min_{x_1, x_2} x_1+x_2\\ s.t.\ x_1^2 +x_2^2 - 1 \leq 0x1,x2minx1+x2s.t. x12+x22−1≤0

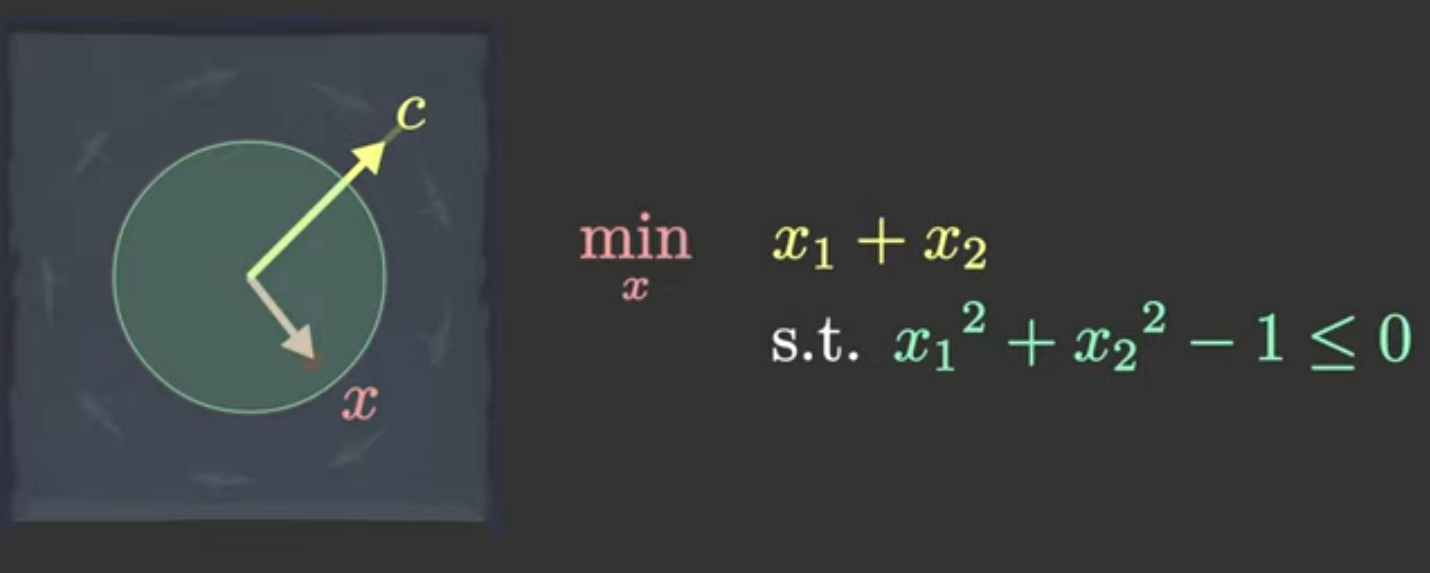
我们先考虑无约束优化版本，它的目标函数值可视化后长这样：

但是只考虑无约束优化的话显然不够。我们需要考虑约束。一种常见的约束处理方法是，把约束作为惩罚项加到优化目标中：
min⁡xx1+x2+P(x12+x22−1)\min_x x_1+x_2 + P(x_1^2 +x_2^2 - 1)xminx1+x2+P(x12+x22−1)

其中P(x12+x22−1)P(x_1^2 +x_2^2 - 1)P(x12+x22−1)是基于约束条件构造的惩罚函数。

为了和原问题保持一致，我们可以取函数PPP如下：

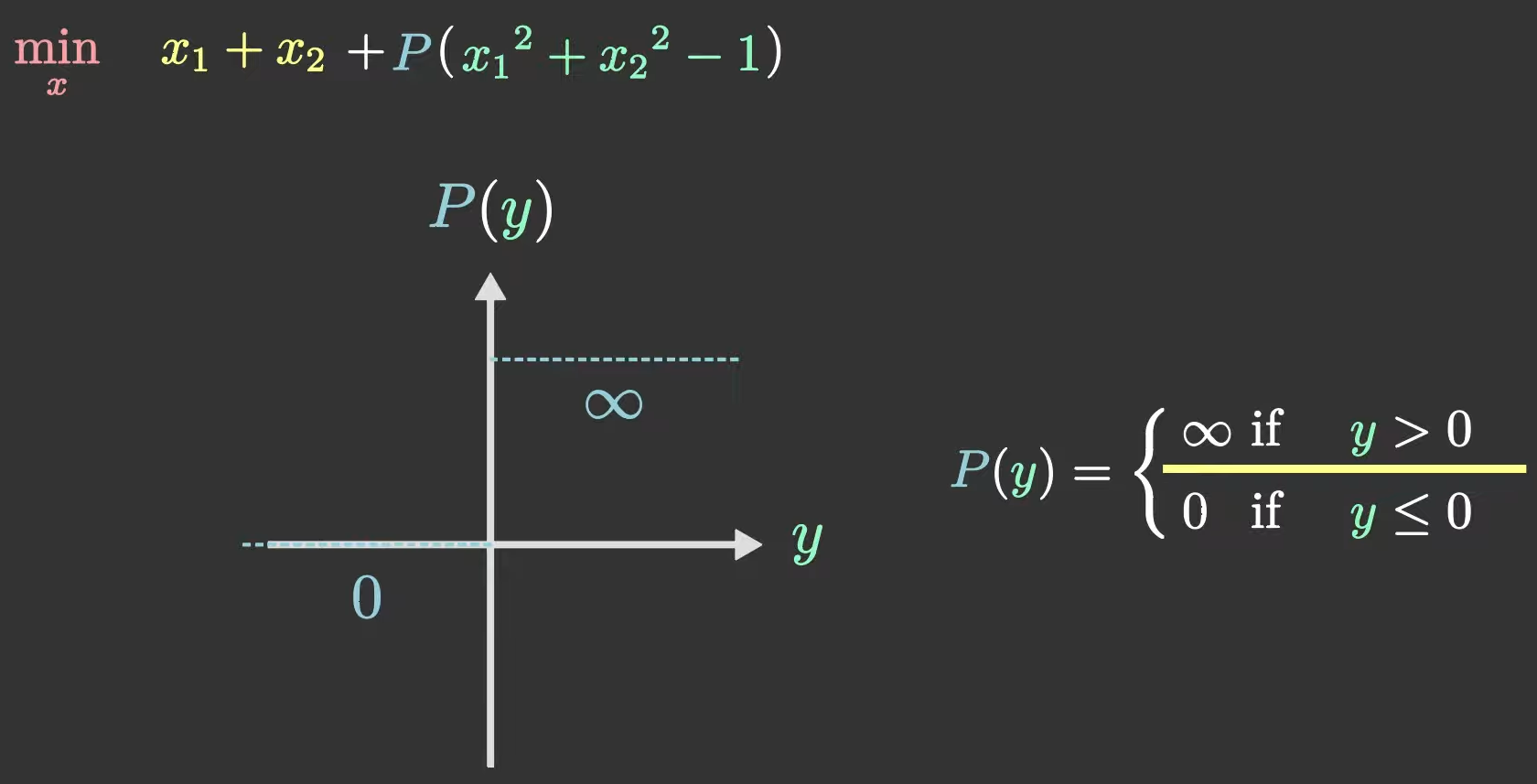
这个PPP函数的定义方法做到了忠于原作（原问题），除了一点，就是没法微分。

另一种方法是选择PPP函数为linear函数，此即P(y)=u×yP(y) = u \times yP(y)=u×y，其中u>0u > 0u>0。

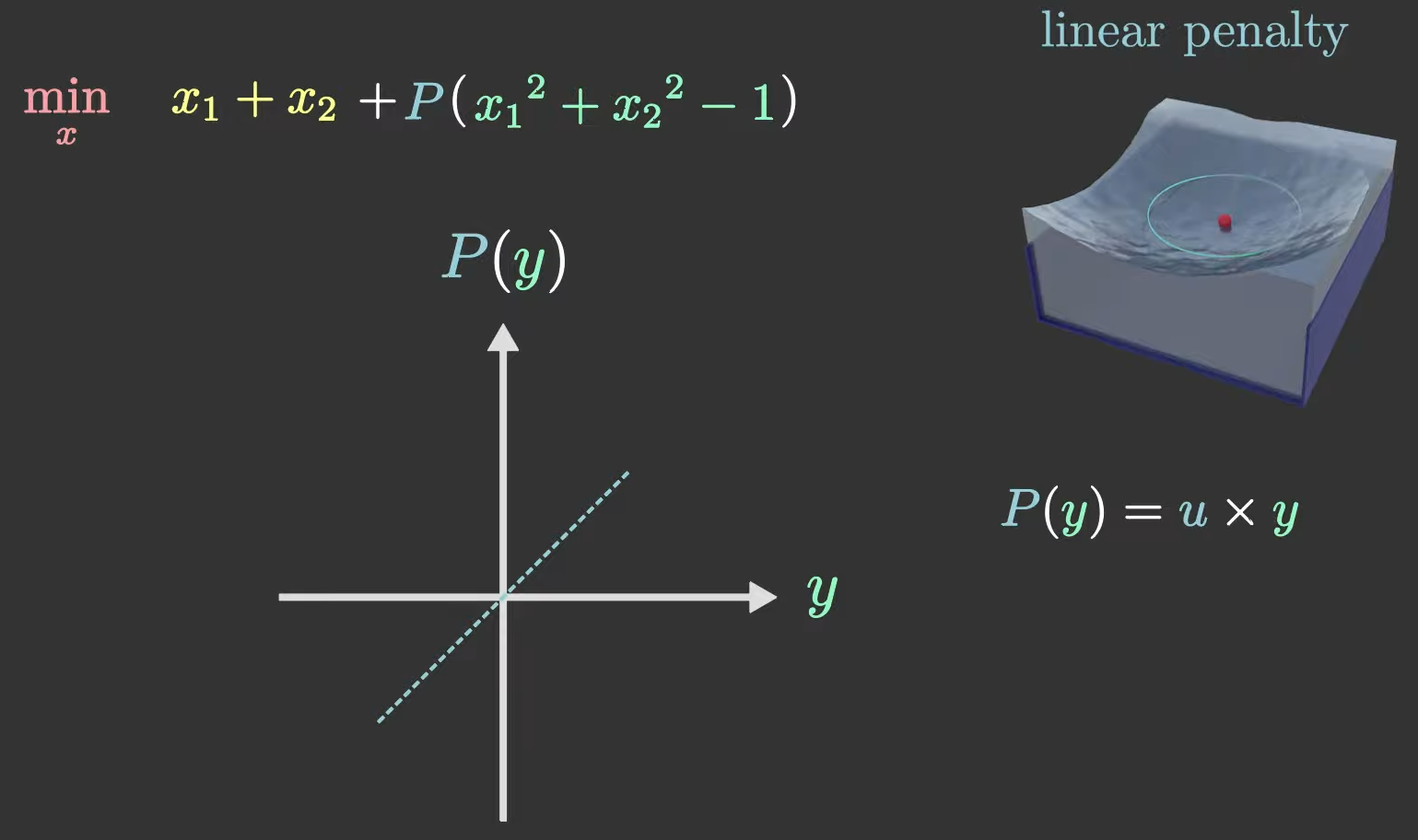这个PPP函数可以微分，但是对原问题做了一通改编。比如：

如果(x1,x2)(x_1, x_2)(x1,x2)满足约束（即x12+x22−1≤0x_1^2 + x_2^2 - 1 \leq 0x12+x22−1≤0），那么它其实应该算作某种奖励，减少了目标函数值。

被奖励多少/惩罚多少又取决于u的值即斜率。u越大，奖惩力度越大。

特殊地，如果我们取P(y)=max⁡u≥0u×yP(y)=\max_{u \geq 0} u \times yP(y)=maxu≥0u×y，则这个优化问题又忠于原作（原问题）了。

我们把上面提到的这个问题好好写一下：
min⁡xmax⁡u≥0x1+x2+u(x12+x22−1)\min_x \max_{u \geq 0} x_1 + x_2 + u(x_1^2 + x_2^2 -1)xminu≥0maxx1+x2+u(x12+x22−1)

这就像一个Stackelberg博弈问题。具体说，博弈双方AAA, BBB分别持xxx和uuu。

在博弈开始，AAA先选定xxx，然后BBB根据AAA的选择结果确定一个uuu。

AAA提出抗议，这么玩没有什么意义。如果AAA先手的话，BBB根据约束的值来确定uuu，如果约束值为非正，则u=0u = 0u=0，否则直接把uuu拉爆到正无穷。结果是平凡的。

如果调换一下博弈顺序，BBB先选定uuu，然后AAA根据uuu的值选定xxx，那么情况会起一些变化：

max⁡u≥0min⁡xx1+x2+u(x12+x22−1)\max_{u \geq 0} \min_x x_1 + x_2 + u(x_1^2 + x_2^2 -1)u≥0maxxminx1+x2+u(x12+x22−1)

在给定任意一个uuu时，AAA只需要把uuu当成参数，然后可以求出来最优的x1,2∗=x1,2(u)=−12ux_{1,2}^* = x_{1,2}(u)= \frac{-1}{2u}x1,2∗=x1,2(u)=2u−1。

最后问题就可以简化为：

max⁡u≥0−u−12u\max_{u \geq 0} -u - \frac{1}{2u}u≥0max−u−2u1

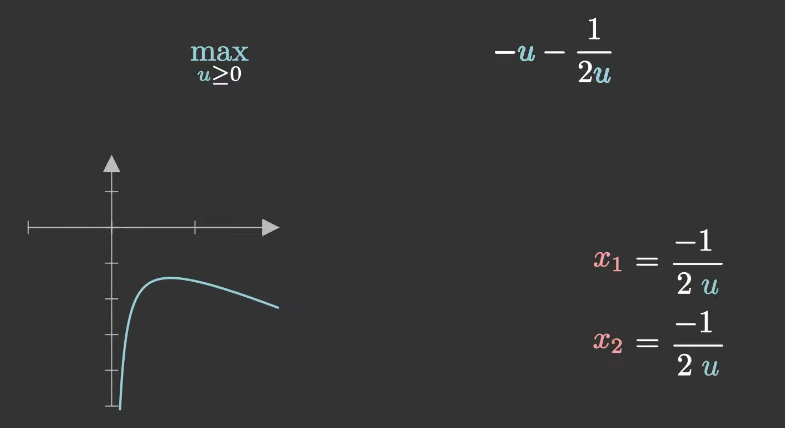
在上述问题中，

原问题：
min⁡xmax⁡u≥0x1+x2+u(x12+x22−1)\min_x \max_{u \geq 0} x_1 + x_2 + u(x_1^2 + x_2^2 -1)xminu≥0maxx1+x2+u(x12+x22−1)

原问题的对偶问题：
max⁡u≥0min⁡xx1+x2+u(x12+x22−1)\max_{u \geq 0} \min_x x_1 + x_2 + u(x_1^2 + x_2^2 -1)u≥0maxxminx1+x2+u(x12+x22−1)

对偶性

下面正式地说明原问题和对偶问题是什么。

考虑优化问题：

min⁡x∈Rnf(x)s.t. hi(x)=0,gj(x)≤0.\min_{x\in \mathbb{R}^n} f(x) \\ s.t. \ \ h_i(x) = 0, \\ g_j(x) \leq 0.x∈Rnminf(x)s.t. hi(x)=0,gj(x)≤0.

先给原问题改写成这个形式：

min⁡x∈Rnf(x)+max⁡vi∈R,uj≥0∑ivihi(x)+∑jujgj(x).\min_{x\in \mathbb{R}^n} f(x)+ \max_{v_i \in \mathbb{R}, u_j \geq 0} \sum_i v_i h_i(x) + \sum_j u_j g_j(x).x∈Rnminf(x)+vi∈R,uj≥0maxi∑vihi(x)+j∑ujgj(x).

称f(x)+∑ivihi(x)+∑jujgj(x)f(x)+ \sum_i v_i h_i(x) + \sum_j u_j g_j(x)f(x)+∑ivihi(x)+∑jujgj(x)为原优化问题的Lagrange函数。

然后做min, max 的调换，得到原问题的对偶问题：

max⁡vi∈R,uj≥0min⁡x∈Rnf(x)+∑ivihi(x)+∑jujgj(x).\max_{v_i \in \mathbb{R}, u_j \geq 0} \min_{x\in \mathbb{R}^n} f(x)+ \sum_i v_i h_i(x) + \sum_j u_j g_j(x).vi∈R,uj≥0maxx∈Rnminf(x)+i∑vihi(x)+j∑ujgj(x).

如图，我们可以得到性质：对偶问题的值是小于原问题的值的。因为先手是外层的max⁡\maxmax优化，在给定u,vu, vu,v的值之后，xxx的取值不会大于右边的原问题。

对偶问题的值小于原问题的值，这是弱对偶性。

还有强对偶性，此时对偶问题和原问题的目标函数值相等。

下面，假设强对偶性成立，看一下KKT条件。

KKT条件

给定u,vu, vu,v，AAA试图最优化自己的目标函数：

min⁡x∈Rnf(x)+∑ivihi(x)+∑jujgj(x).\min_{x\in \mathbb{R}^n} f(x)+\sum_i v_i h_i(x) + \sum_j u_j g_j(x).x∈Rnminf(x)+i∑vihi(x)+j∑ujgj(x).

在最优点时，Lagrange函数的梯度应该为0，即∇[f(x)+∑ivihi(x)+∑jujgj(x)]=0\nabla[f(x)+ \sum_i v_i h_i(x) + \sum_j u_j g_j(x)] = 0∇[f(x)+∑ivihi(x)+∑jujgj(x)]=0

梯度为0是必要条件，即最优解必须满足梯度为0，梯度不为0则必不是最优解。

为简便起见，我们暂时仅考虑一个不等式约束。于是有：
∇f(x)=−u∇g(x)\nabla f(x) = -u \nabla g(x)∇f(x)=−u∇g(x)

这表明fff的梯度应该和ggg的梯度向量共线。

如果两个梯度向量不共线的话，如下图。在xxx点处，总是可以试探一个方向（那个粉色的x处），这个点的函数值更小，即xxx点处的fff值并不是最小。

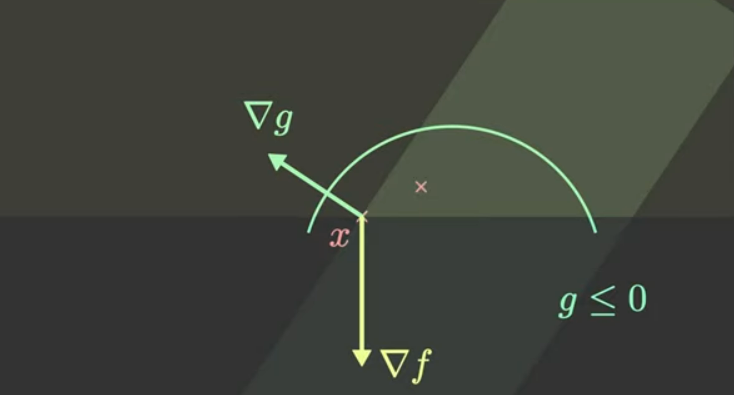
如下图是fff的梯度和ggg的梯度向量共线的情况。

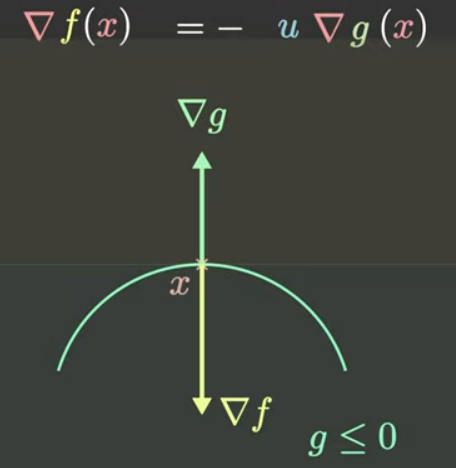
现在已知从左往右是成立的，即最优点xxx应该满足Lagrange函数导数为0。

但是从右往左还不够。如下图，KKT条件才能够保证从右往左成立。

但是大规模优化问题的KKT条件计算起来比较费事。因此有内点法。

内点法

使用内点法时，并不是求解KKT条件，而是求解

KKT(t),t>0KKT(t), t > 0KKT(t),t>0

将ug(x)=0ug(x) = 0ug(x)=0换为ug(x)=−tug(x)=-tug(x)=−t，得到最优的x=x(t)x = x(t)x=x(t)。随着t→0t \to 0t→0，得到x(t)→x∗x(t) \to x^*x(t)→x∗。

我们将KKT(t)重写一遍：

然后做一系列的反解。

最后发现KKT(t)问题其实就是右边优化问题的KKT条件，左边的约束条件还都是天然成立的。

因为，ggg在对数函数内，天然要求g<0g < 0g<0。最后一个式子定义的uuu也是天然为正。

右边的优化问题从定义上就满足了约束条件，也就是说它其实是一个无约束优化问题，直接上牛顿法就可以了。

上述推导仅考虑不等式约束。带有等式约束的情形留作习题。

对上述内点法的一个直观理解如下：ttt决定了log约束函数的大小。ttt越大，则整个目标函数收到log约束的影响越大，于是希望ttt足够小，使得目标函数被惩罚项的影响尽量少。

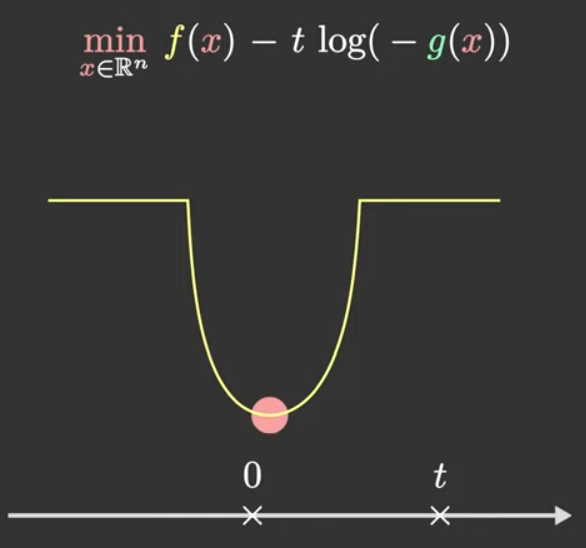
但是ttt太小的话，牛顿法的可能收敛得很慢，如下图所示，因为fff的底很平，拿不到什么太大的梯度。

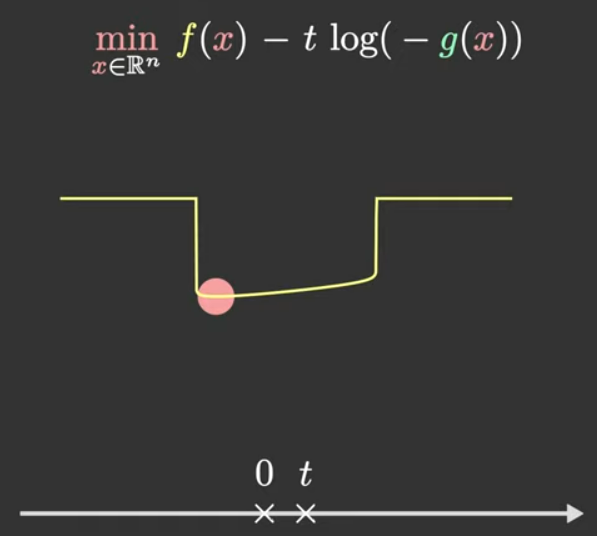
另一个想法是，我们不需要ttt在一开始就取得很小，可以让ttt从大逐渐变小。

首先，一开始取很大的ttt意味着让整个目标函数大部分是g，先找到g(x)≤0g(x)\leq 0g(x)≤0的"中心"，然后逐步缩小ttt，以前一步的xxx作为初始点。

因为ttt的变动很小，导致初值离可能的最优点比较近，此时的牛顿法收敛速度会非常快。