[算法]---路径问题

目录

[1. 不同路径](#1. 不同路径)

[1.1 解题思路](#1.1 解题思路)

[1.2 代码实现](#1.2 代码实现)

[2. 不同路径2](#2. 不同路径2)

[2.1 解题思路](#2.1 解题思路)

[2.2. 代码实现](#2.2. 代码实现)

[3. 珠宝的最高价值](#3. 珠宝的最高价值)

[3.1 解题思路](#3.1 解题思路)

[3.2 代码实现](#3.2 代码实现)

[4. 下降路径最小和](#4. 下降路径最小和)

[4.1 解题思路](#4.1 解题思路)

[4.2 代码实现](#4.2 代码实现)

[5. 最小路径和](#5. 最小路径和)

[5.1 解题思路](#5.1 解题思路)

[5.2 代码实现](#5.2 代码实现)

[6. 地下城游戏](#6. 地下城游戏)

[6.1 解题思路](#6.1 解题思路)

[6.2 代码实现](#6.2 代码实现)

---

1. 不同路径

题目链接

1.1 解题思路

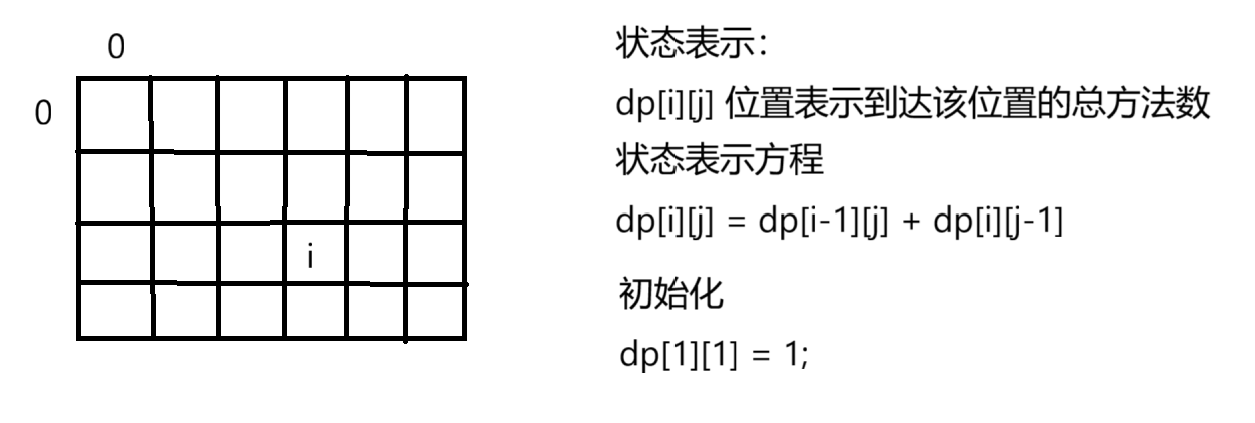
1.2 代码实现

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m + 1][n + 1];
        dp[1][1] = 1;
        for(int i = 1; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                if(i == 1 && j == 1) continue;
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m][n];
    }
}

2. 不同路径2

题目链接

2.1 解题思路

这里需要注意的是当元素中只有一个障碍物时候，需要返回0，也就是dp11初始化成0。

2.2. 代码实现

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m + 1][n + 1];
        if(obstacleGrid[0][0] != 1) dp[1][1] = 1;
        for(int i = 1; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                if(i == 1 && j == 1) continue;
                if(obstacleGrid[i - 1][j - 1] != 1) {
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }
            }
        }
        return dp[m][n];
    }
}

3. 珠宝的最高价值

题目链接

3.1 解题思路

3.2 代码实现

class Solution {
    public int jewelleryValue(int[][] frame) {
        int m = frame.length;
        int n = frame[0].length;
        int[][] dp = new int[m + 1][n + 1];

        for(int i = 1; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                dp[i][j] = Math.max(dp[i][j-1] + frame[i-1][j-1], dp[i-1][j] + frame[i-1][j-1]);
            }
        }
        return dp[m][n];
    }
}

4. 下降路径最小和

题目链接

4.1 解题思路

4.2 代码实现

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] dp = new int[m + 1][n + 2];
        int minNum = Integer.MAX_VALUE;
        for(int i = 1; i <= m; i++) {
            dp[i][0] = Integer.MAX_VALUE;
            dp[i][n+1] = Integer.MAX_VALUE;
        }

        for(int i = 1; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                dp[i][j] = Math.min(Math.min(dp[i-1][j-1], dp[i-1][j]), dp[i-1][j+1]) + matrix[i-1][j-1];
            }
        }
        for(int k = 1; k <= n; k++) {
            minNum = Math.min(minNum, dp[m][k]);
        }
        return minNum;
    }
}

5. 最小路径和

题目链接

5.1 解题思路

5.2 代码实现

class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m + 1][n + 1];
        //初始化
        for (int i = 2; i <= m; i++) {
            dp[i][0] = Integer.MAX_VALUE;
        }
        for (int i = 2; i <= n; i++) {
            dp[0][i] = Integer.MAX_VALUE;
        }
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
            }
        }
        return dp[m][n];
    }
}

6. 地下城游戏

题目链接

6.1 解题思路

6.2 代码实现

class Solution {
    public int calculateMinimumHP(int[][] dungeon) {
        int m = dungeon.length;
        int n = dungeon[0].length;
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 0; i <= m - 2; i++) {
            dp[i][n] = Integer.MAX_VALUE;
        }
        for (int j = 0; j <= n - 2; j++) {
            dp[m][j] = Integer.MAX_VALUE;
        }
        dp[m - 1][n] = dp[m][n - 1] = 1;
        for (int i = m - 1; i >= 0; i--) {
            for (int j = n - 1; j >= 0; j--) {
                dp[i][j] = Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];
                dp[i][j] = Math.max(1, dp[i][j]);
            }
        }
        return dp[0][0];
    }
}