在Spark中,宽窄依赖(Narrow and Wide Dependencies)是理解分布式计算和数据流动的关键概念,其特性与"宽窄巷子"的比喻有相似之处:
1、什么是依赖关系?

2、什么是宽窄依赖?
窄依赖:Narrow Dependencies
定义:父RDD的一个分区的数据只给了子RDD的一个分区 【 不用经过Shuffle 】
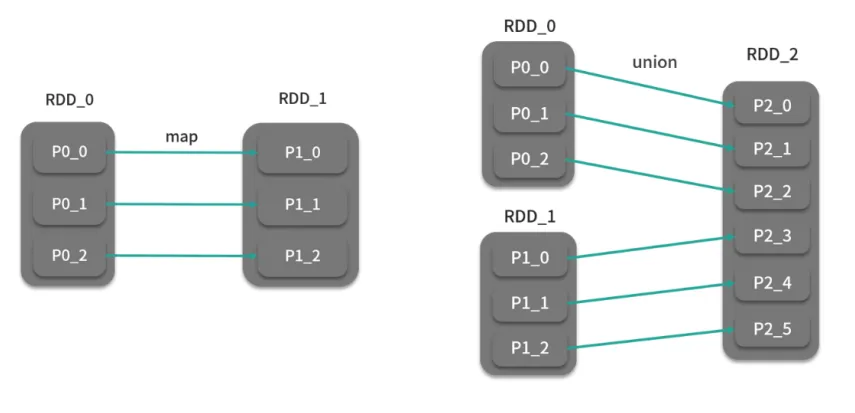
窄依赖(Narrow Dependency)
- 定义 :子RDD的每个分区仅依赖于父RDD的一个分区 (如
map、filter操作)。 - 特点 :
-
数据无需跨节点移动(本地计算)
-
高效且容错简单(只需重算单个分区)
-
类似窄巷子:数据流单向、并行,无交叉
窄依赖示例:map操作
rdd = sc.parallelize([1, 2, 3])
mapped = rdd.map(lambda x: x * 2) # 子分区仅依赖父RDD的同一分区
-
宽依赖(Wide Dependency)
- 定义 :子RDD的每个分区依赖父RDD的多个分区 (如
groupByKey、reduceByKey)。 - 特点 :
-
需Shuffle操作(数据跨节点重组)
-
可能成为性能瓶颈(网络传输开销)
-
类似宽巷子:多路数据汇聚交叉,需全局协调
宽依赖示例:reduceByKey
rdd = sc.parallelize([("a", 1), ("b", 2), ("a", 3)])
reduced = rdd.reduceByKey(lambda x, y: x + y) # 相同键的数据需从多分区聚合
-
性能优化建议
- 优先使用窄操作 :如用
reduceByKey替代groupByKey(前者局部聚合减少Shuffle数据量) - 调整分区数 :通过
repartition()或coalesce()控制Shuffle粒度 - 持久化中间结果 :对重复使用的宽依赖RDD调用
persist()
数学表达补充
设RDD分区为集合P,依赖关系可形式化定义为: $$ \text{窄依赖:} \quad \forall p_i \in P_{\text{子}}, \ \exists! p_j \in P_{\text{父}} \quad \text{s.t.} \quad p_i \subseteq f(p_j) $$ $$ \text{宽依赖:} \quad \exists p_i \in P_{\text{子}}, \ \ |{p_j \in P_{\text{父}} \mid p_i \cap p_j \neq \emptyset}| > 1 $$ 其中f为转换函数。