（以下内容全部来自上述课程）
目录
- 逻辑门电路（补）
-
- [1. 算数运算vs逻辑运算](#1. 算数运算vs逻辑运算)
- [2. 基础逻辑运算](#2. 基础逻辑运算)
-
- [2.1 与](#2.1 与)
- [2.2 或](#2.2 或)
- [2.3 非](#2.3 非)
- [3. 复合逻辑运算](#3. 复合逻辑运算)
-
- [3.1 与非](#3.1 与非)
- [3.2 或非](#3.2 或非)
- [3.3 异或](#3.3 异或)
- [3.4 同或](#3.4 同或)
- [4. 小结](#4. 小结)
- [5. 补充](#5. 补充)
-
- [5.1 门电路的变形画法](#5.1 门电路的变形画法)
- [5.2 逻辑运算的优先级、常见公式](#5.2 逻辑运算的优先级、常见公式)
- 多路选择器、三态门（补）
-
- [1. 多路选择器](#1. 多路选择器)
- [2. 三态门](#2. 三态门)
- [3. 小结](#3. 小结)
- 加法器
-
- [1. 加法器的基本功能](#1. 加法器的基本功能)
- [2. 一位全加器](#2. 一位全加器)
- [3. n bit加法器](#3. n bit加法器)
- [4. 并行加法器](#4. 并行加法器)
- [5. 带标志位的加法器](#5. 带标志位的加法器)
- [6. 小结](#6. 小结)
- 算术逻辑单位ALU
-
- [1. 作用](#1. 作用)
- [2. 功能](#2. 功能)
- [3. 实现原理（了解）](#3. 实现原理（了解）)
- [4. 看懂图示](#4. 看懂图示)
- [5. 小结](#5. 小结)
- 定点数的移位运算
-
- [1. 逻辑移位（无符号）](#1. 逻辑移位（无符号）)
- [2. 算数移位（带符号）](#2. 算数移位（带符号）)
- [3. 小结](#3. 小结)
- 定点数的加减运算
-
- [1. 原码的加减运算（不考）](#1. 原码的加减运算（不考）)
- [2. 补码的加减运算](#2. 补码的加减运算)
- [3. 溢出判断](#3. 溢出判断)
- [4. 小结](#4. 小结)
- 无符号数的加减运算
-
- [1. 无符号数的加法运算](#1. 无符号数的加法运算)
- [2. 无符号数的减法运算](#2. 无符号数的减法运算)
- [3. 溢出判断](#3. 溢出判断)
- [4. 小结](#4. 小结)
- 补码加减运算电路
逻辑门电路（补）
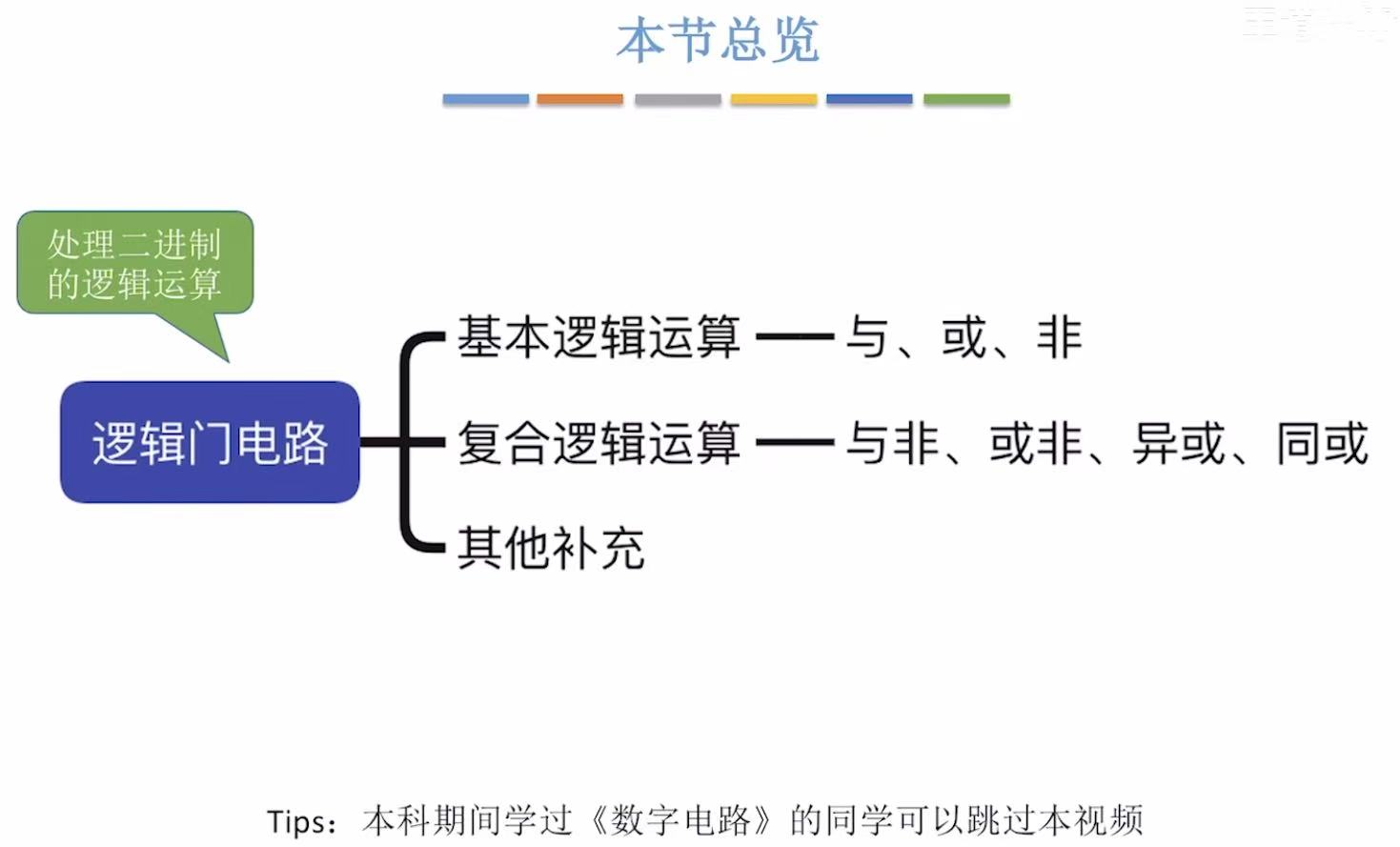
1. 算数运算vs逻辑运算
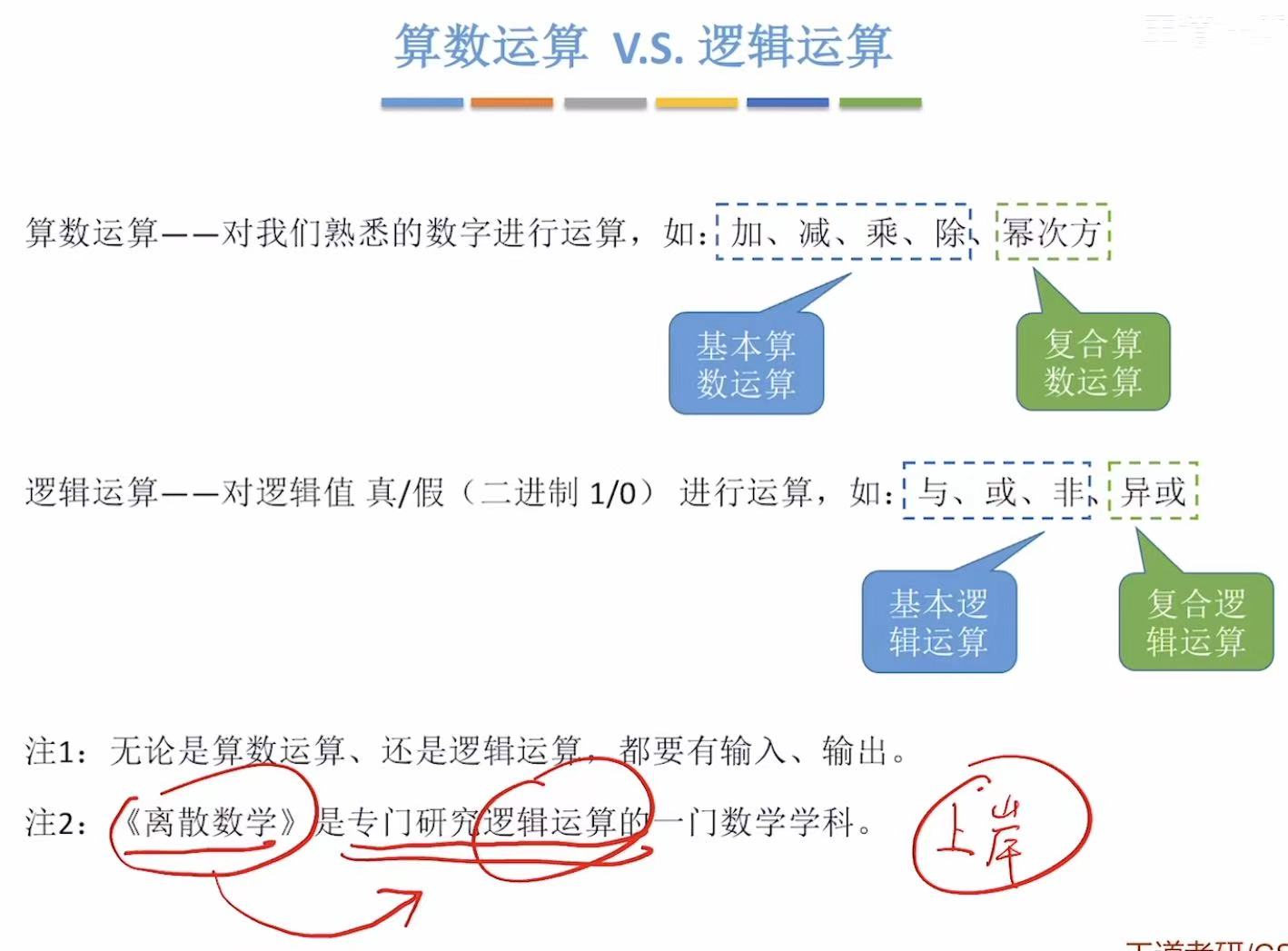
2. 基础逻辑运算
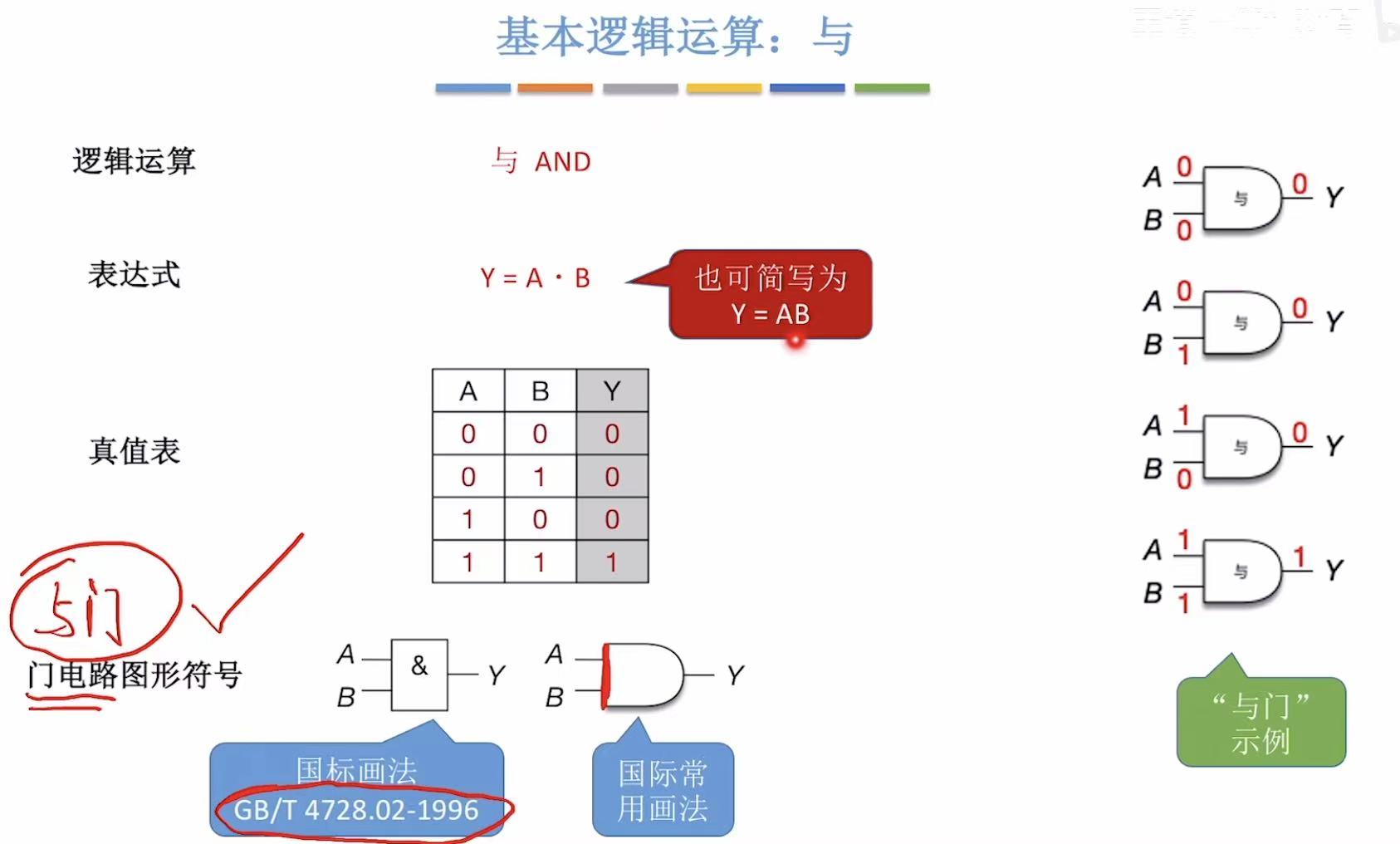
2.1 与
用乘法 理解：00=0、0 1=0、10=0、1 1=1
符号标志 ：竖线＋圆弧
2.2 或
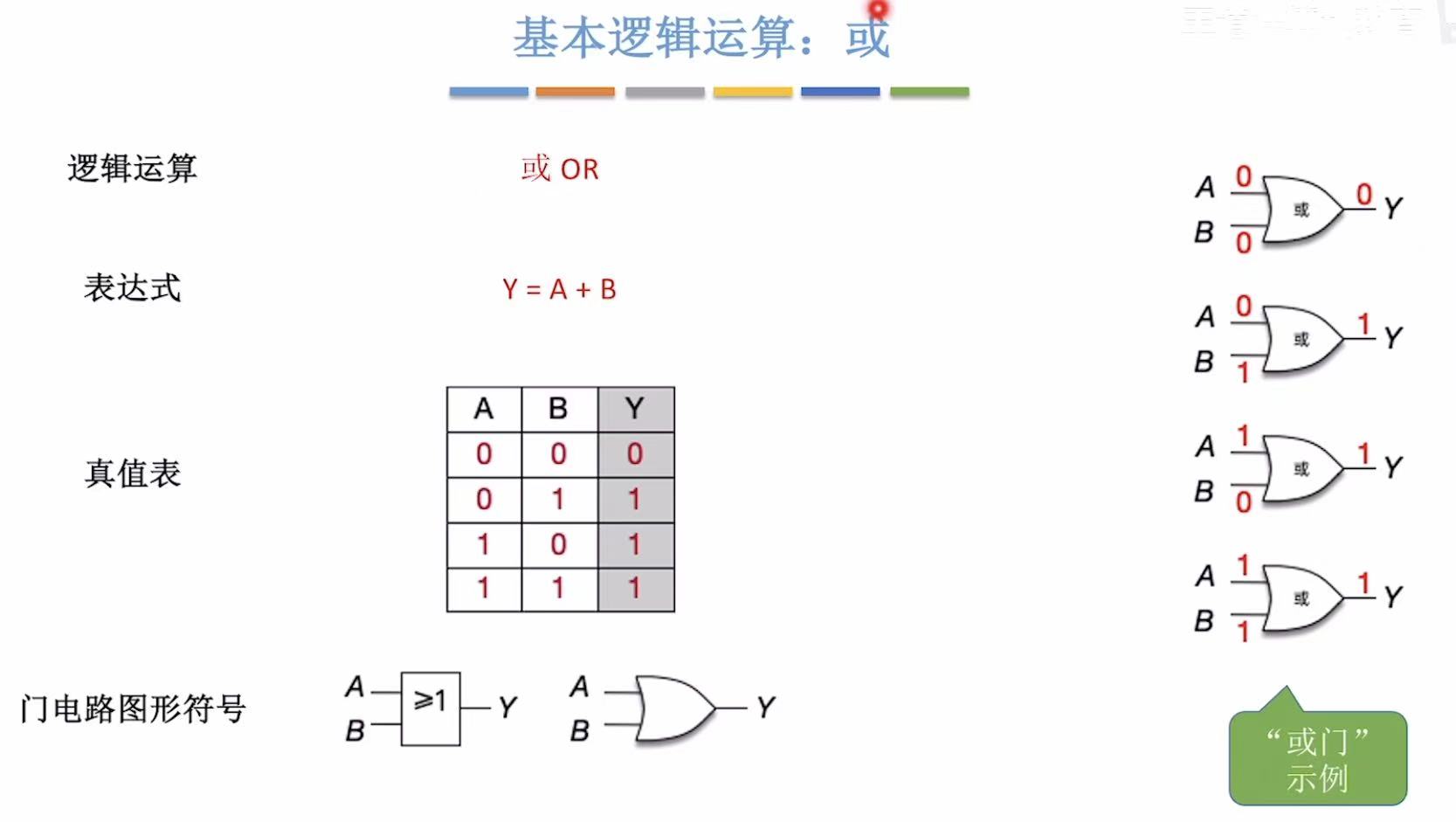
用加法 理解：0+0=0、1+0=1、0+1=1、1+1=2（二进制，表示正确，所以用1表示）
符号标志 ：三角形
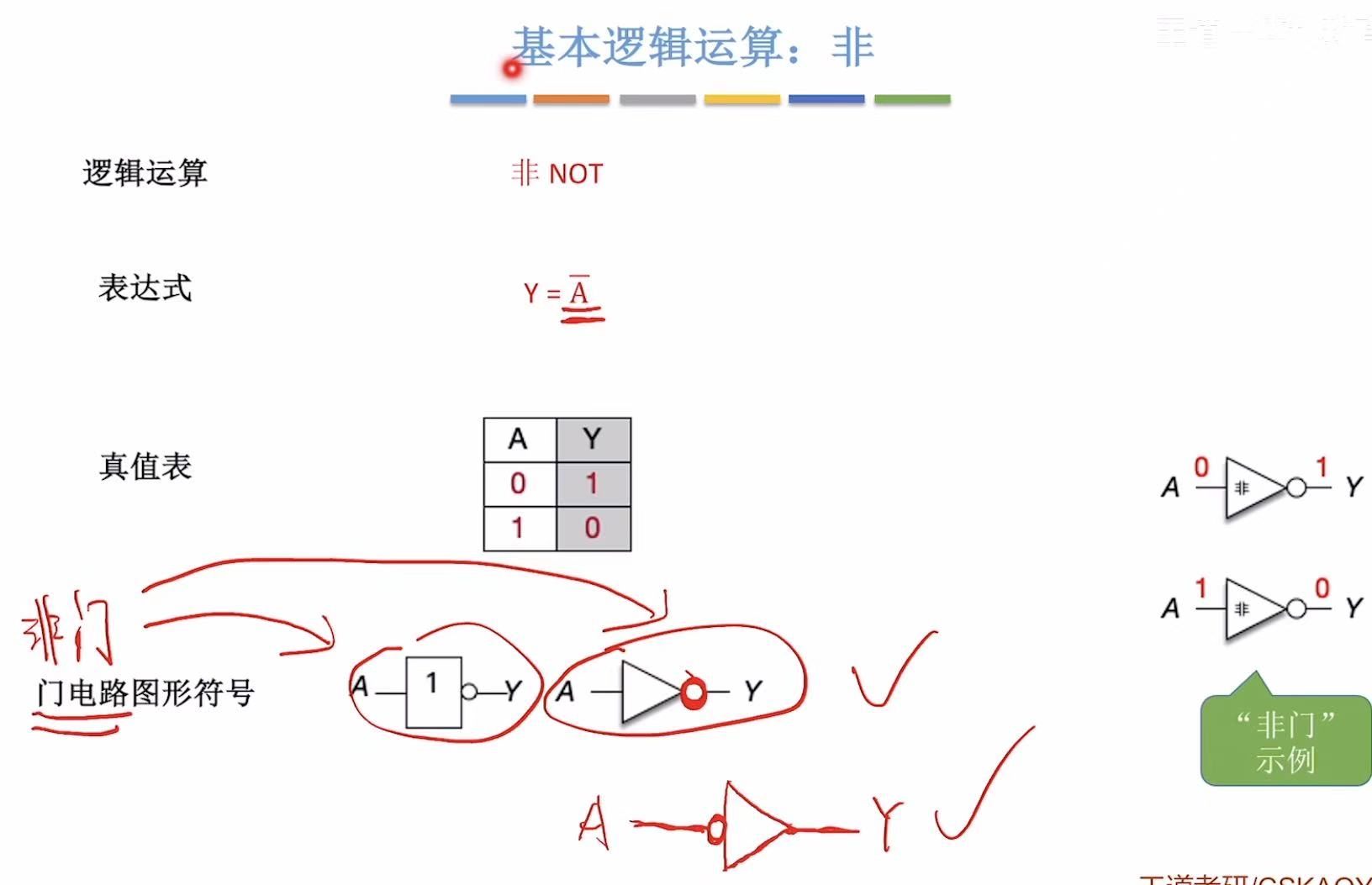
2.3 非
倒置 ：1变为0，0变为1
符号标志 ：小圆圈
3. 复合逻辑运算
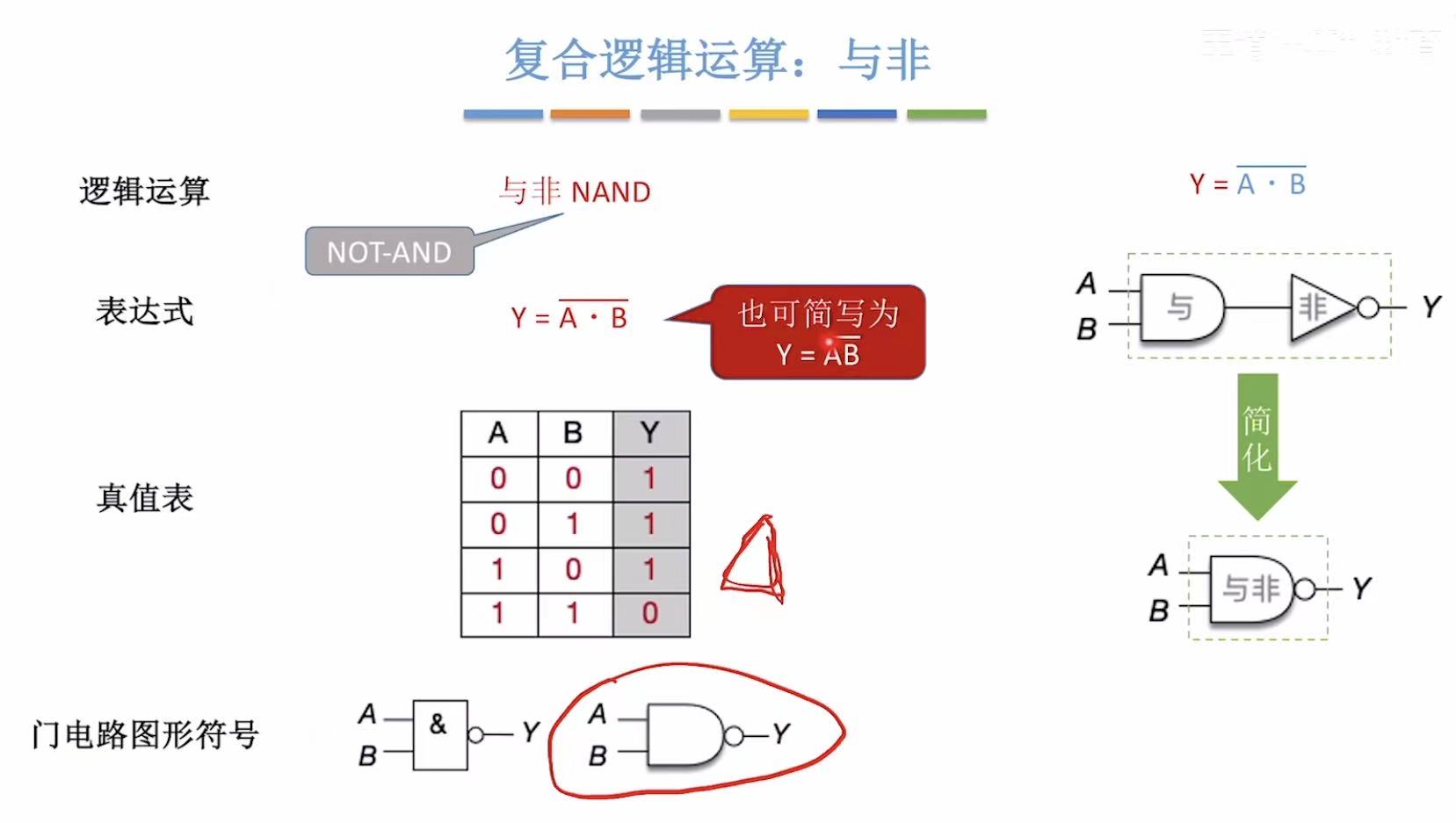
3.1 与非
先与后非 ：先算乘法，然后再倒置。
00=0-->1
0 1=0-->1
10=0-->1
1 1=1-->0
符号标志 ：与＋非-->圆弧＋圆圈
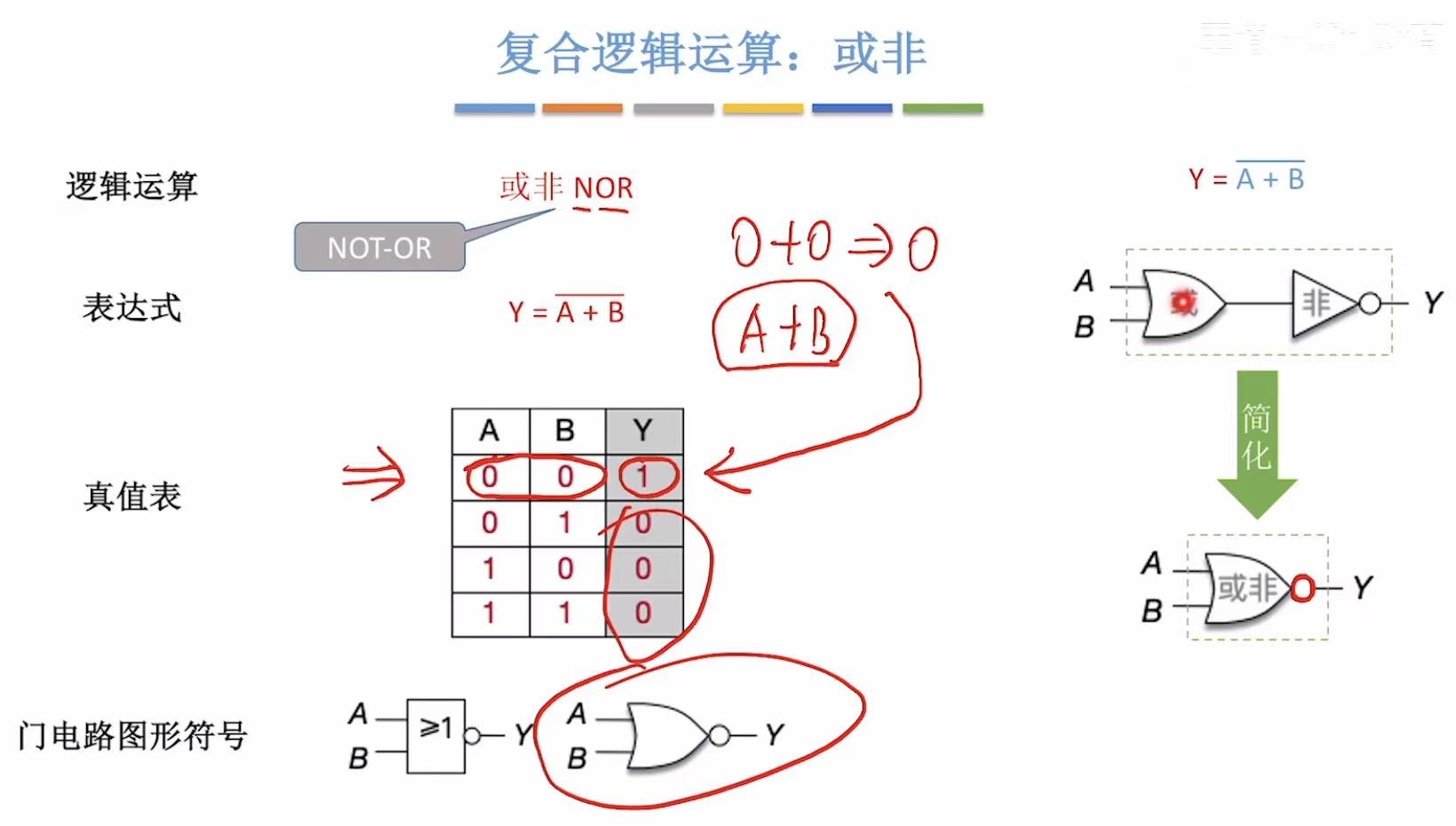
3.2 或非
先或后非 ：先算加法，然后再倒置。
0+0=0-->1
0+1=1-->0
1+0=1-->0
1+1=1-->0
符号标志 ：或+非-->三角形＋圆圈
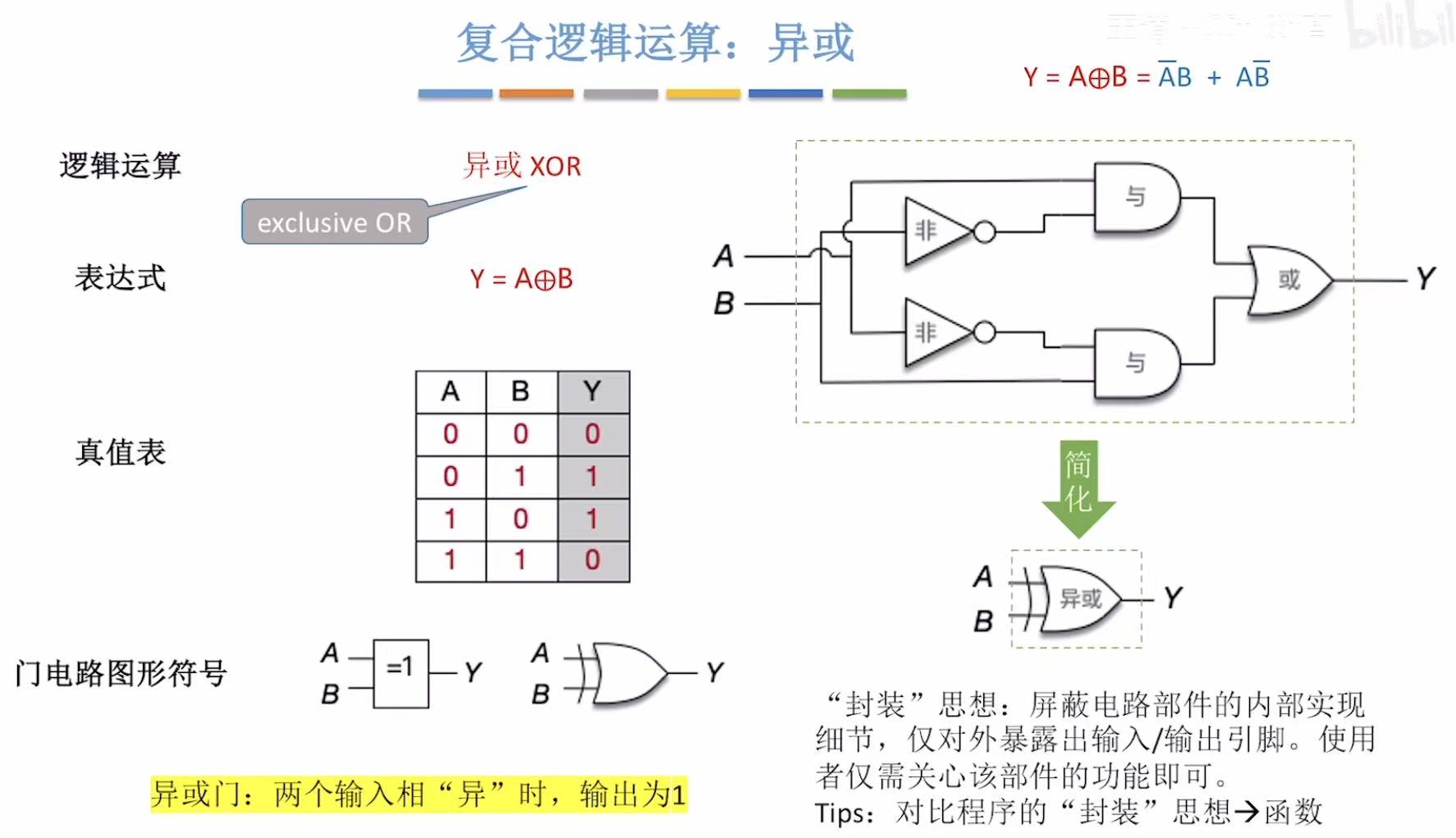
3.3 异或
异或异或，肯定是不一样 （异）的加在一起 （或）才对 （1）。
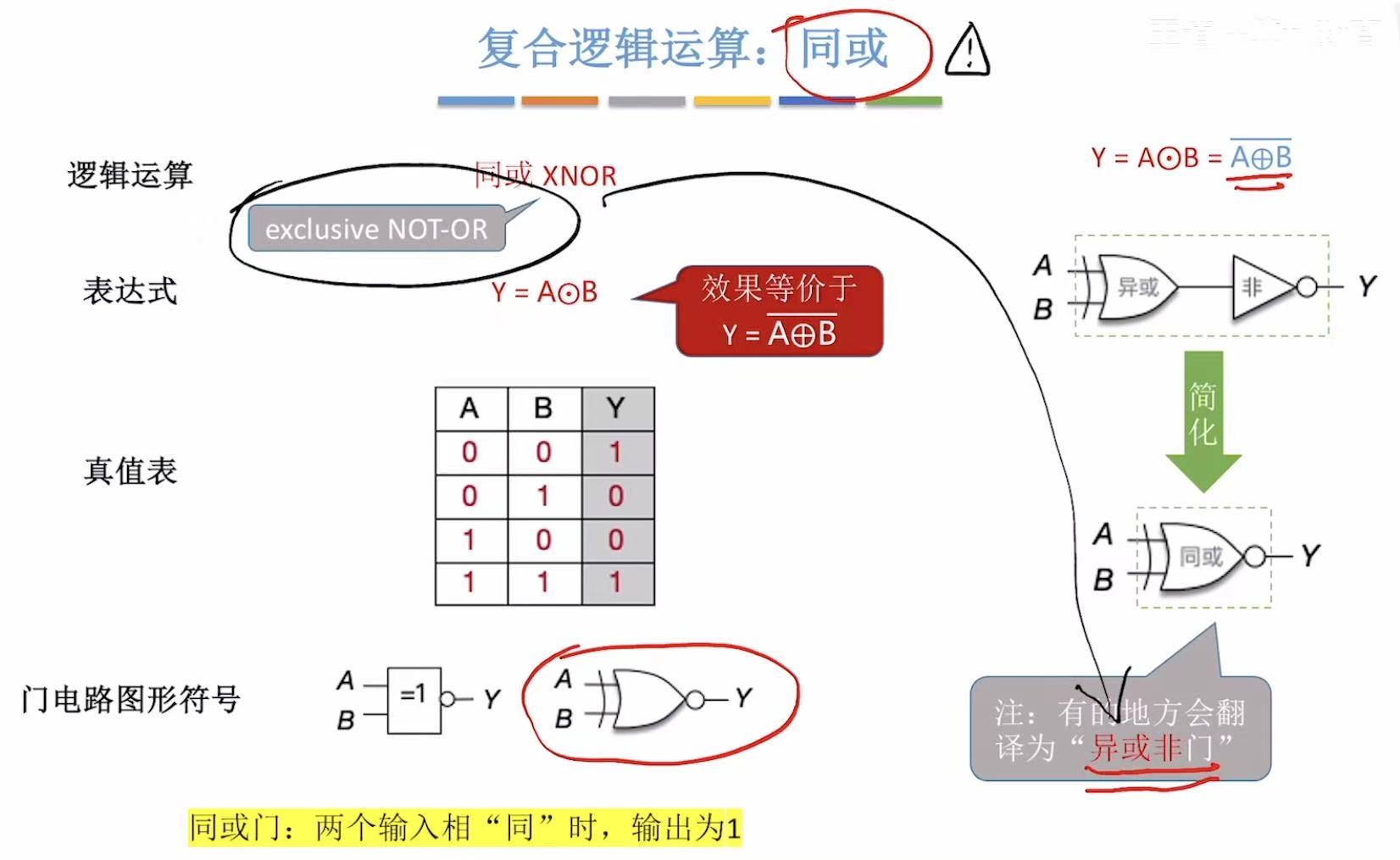
3.4 同或
同或就是异或反过来，或者就见名知意，相同 的（同）加 在一起（或）才对 （1）。
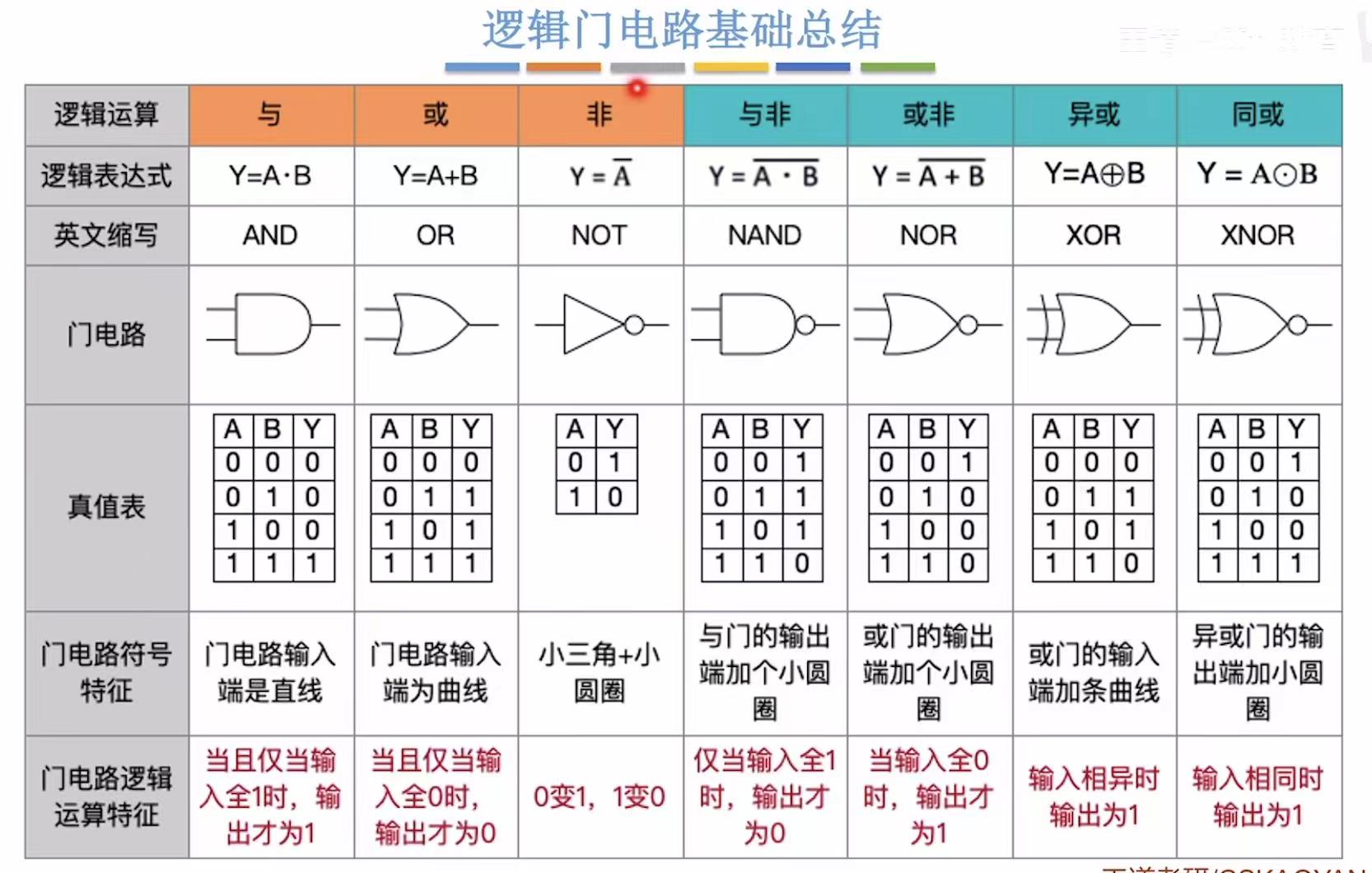
4. 小结
题外话：异或运算的妙用
5. 补充
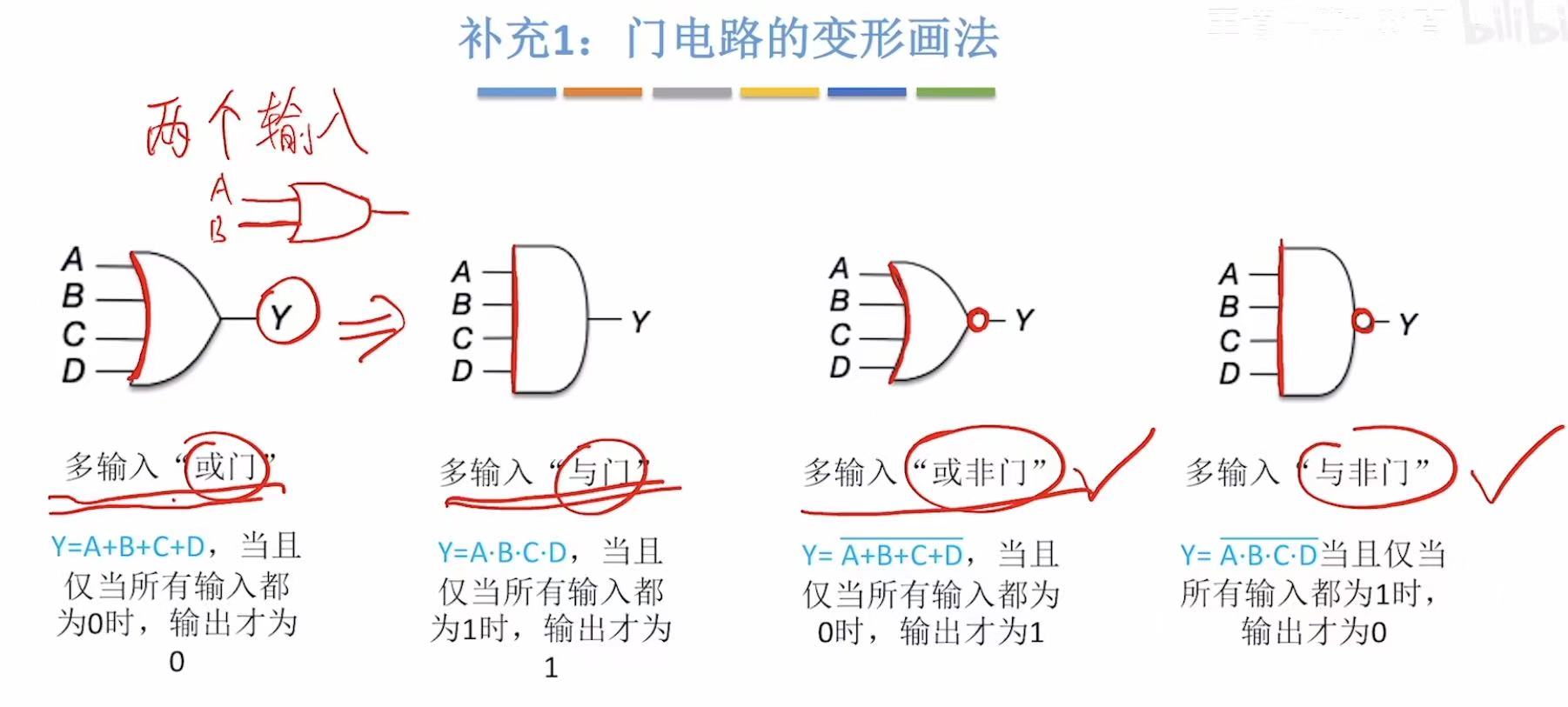
5.1 门电路的变形画法
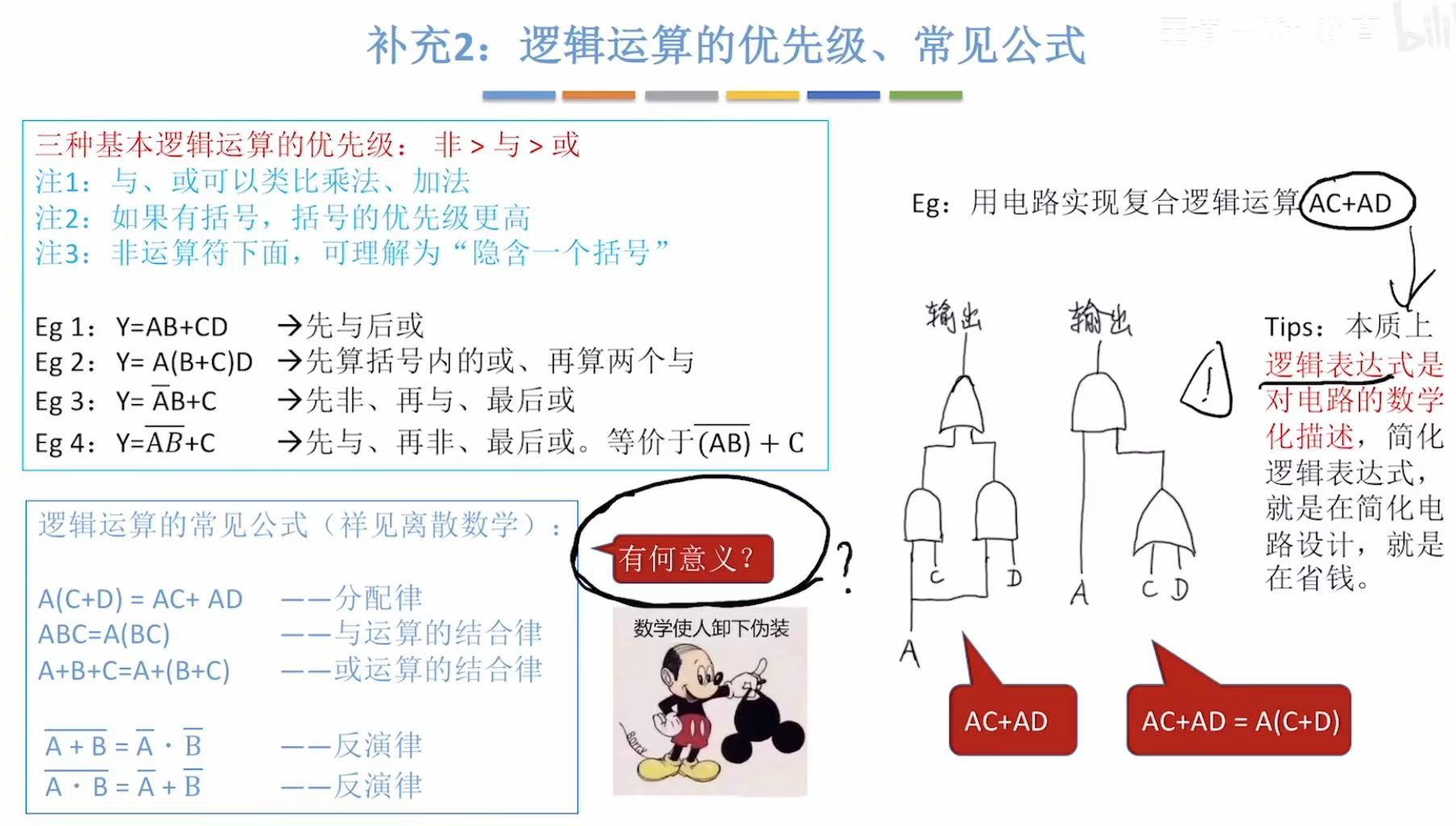
5.2 逻辑运算的优先级、常见公式
拓展：芯片制程
多路选择器、三态门（补）
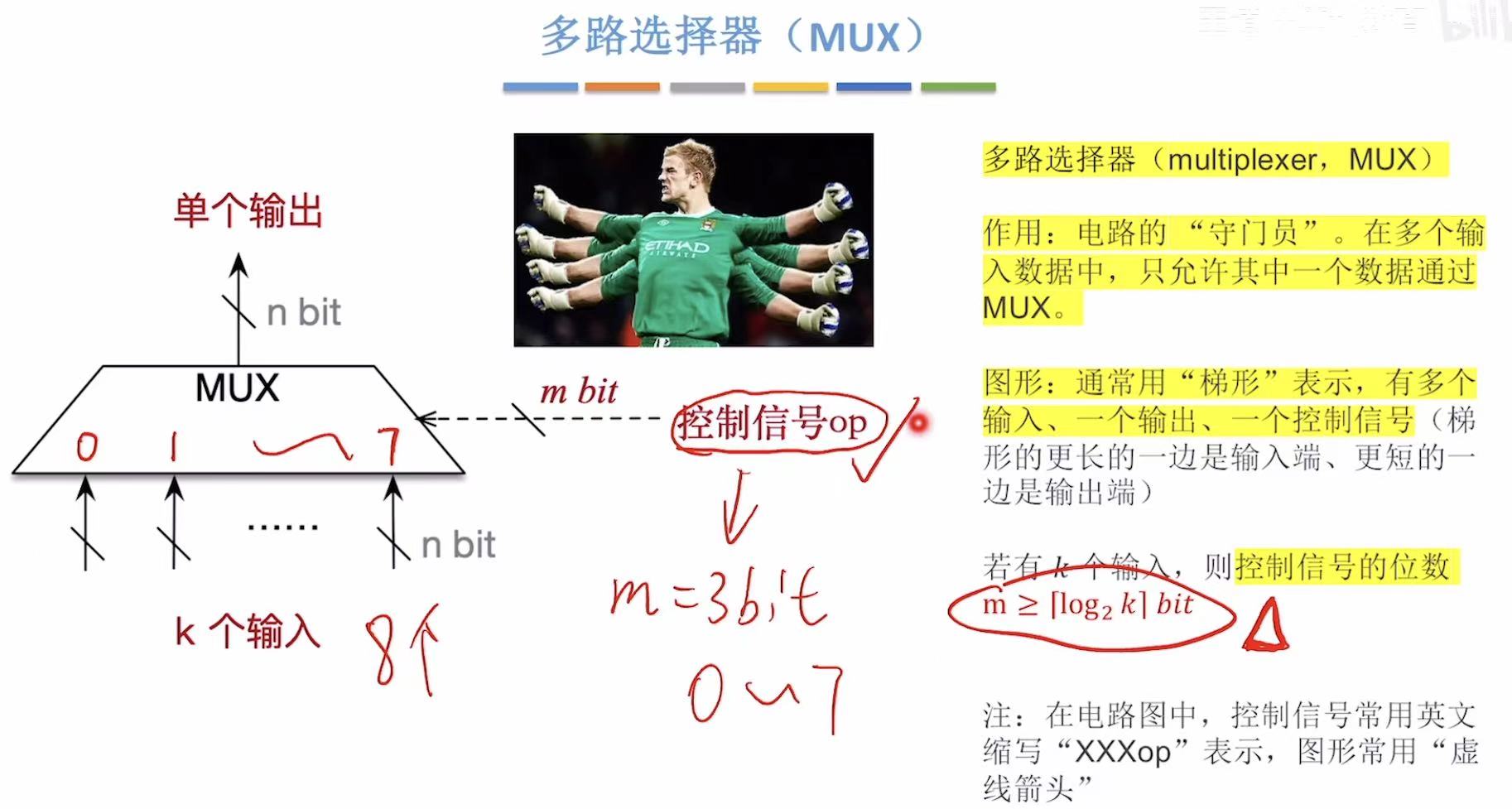
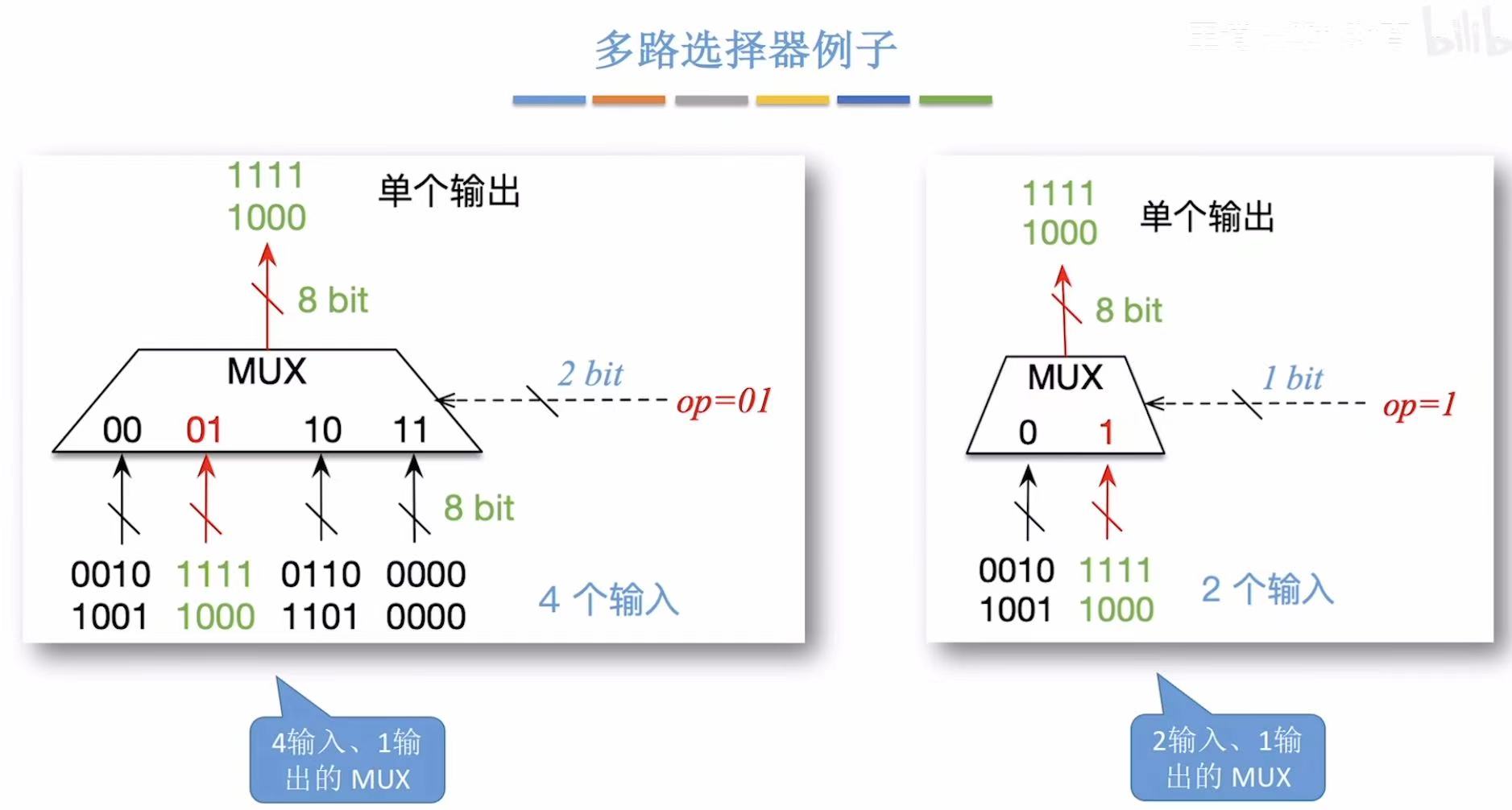
1. 多路选择器
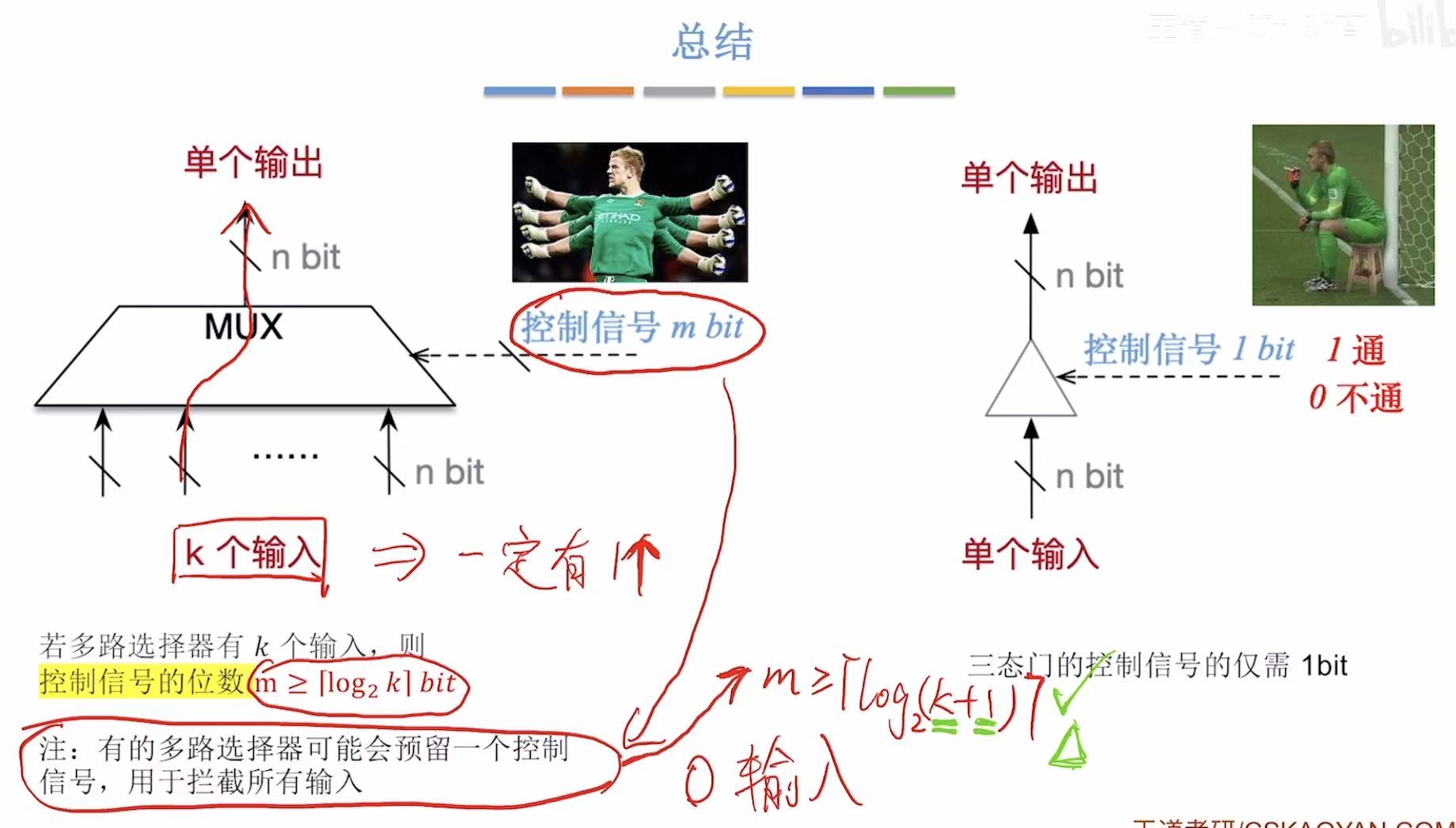
只允许一个数据通过。
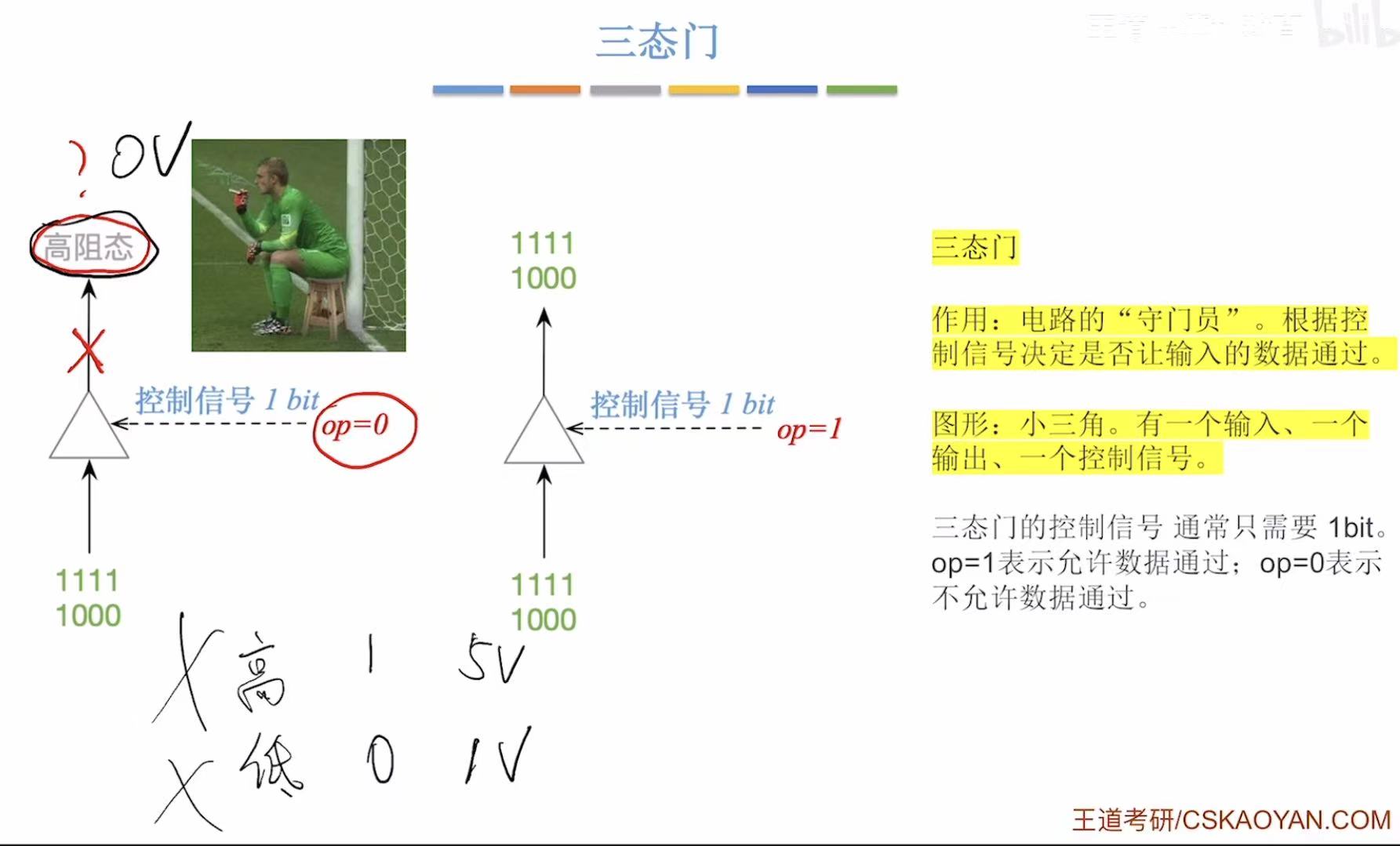
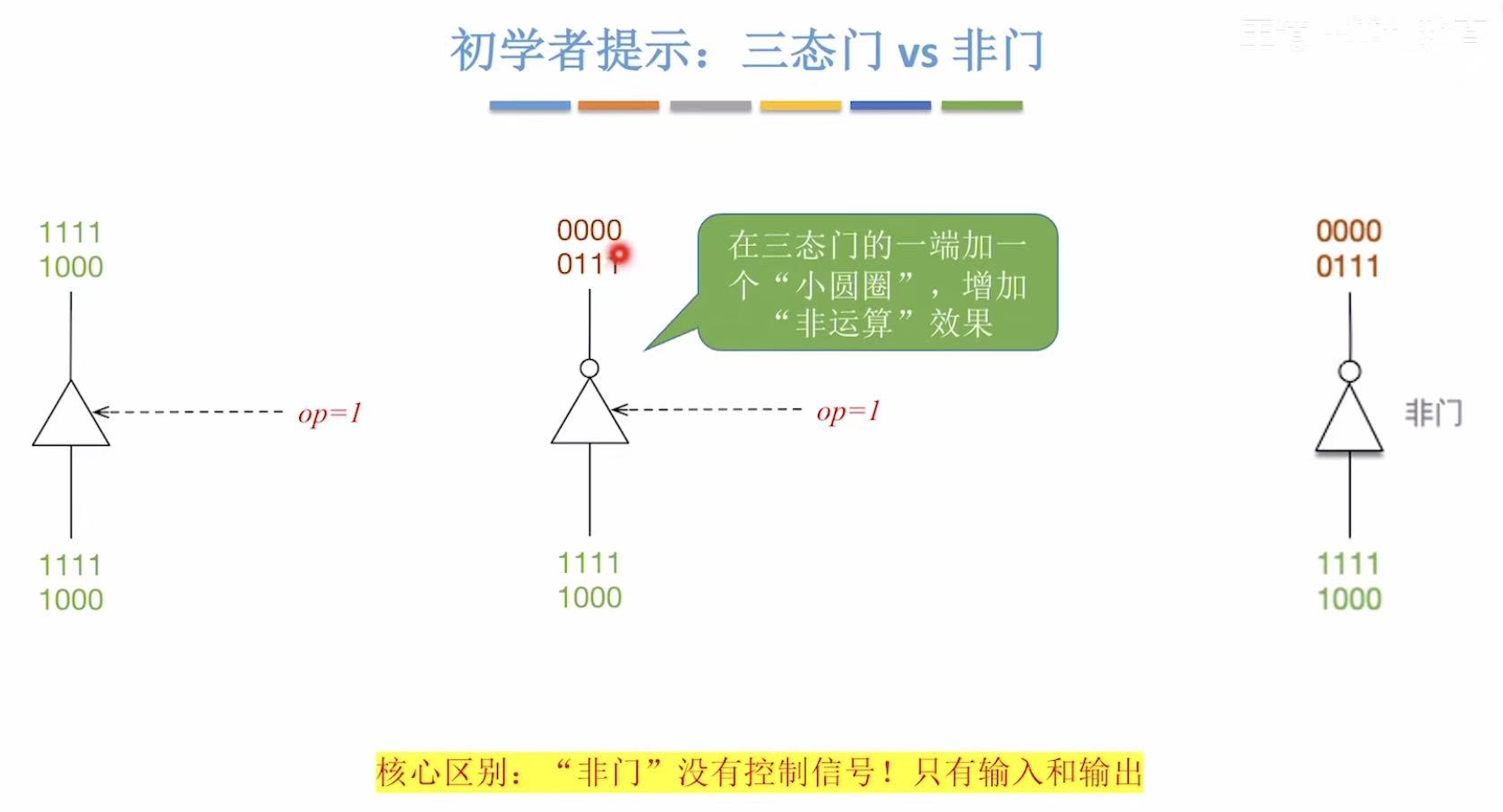
2. 三态门
看让不让过，1就让过，0就不让过。
3. 小结
加法器
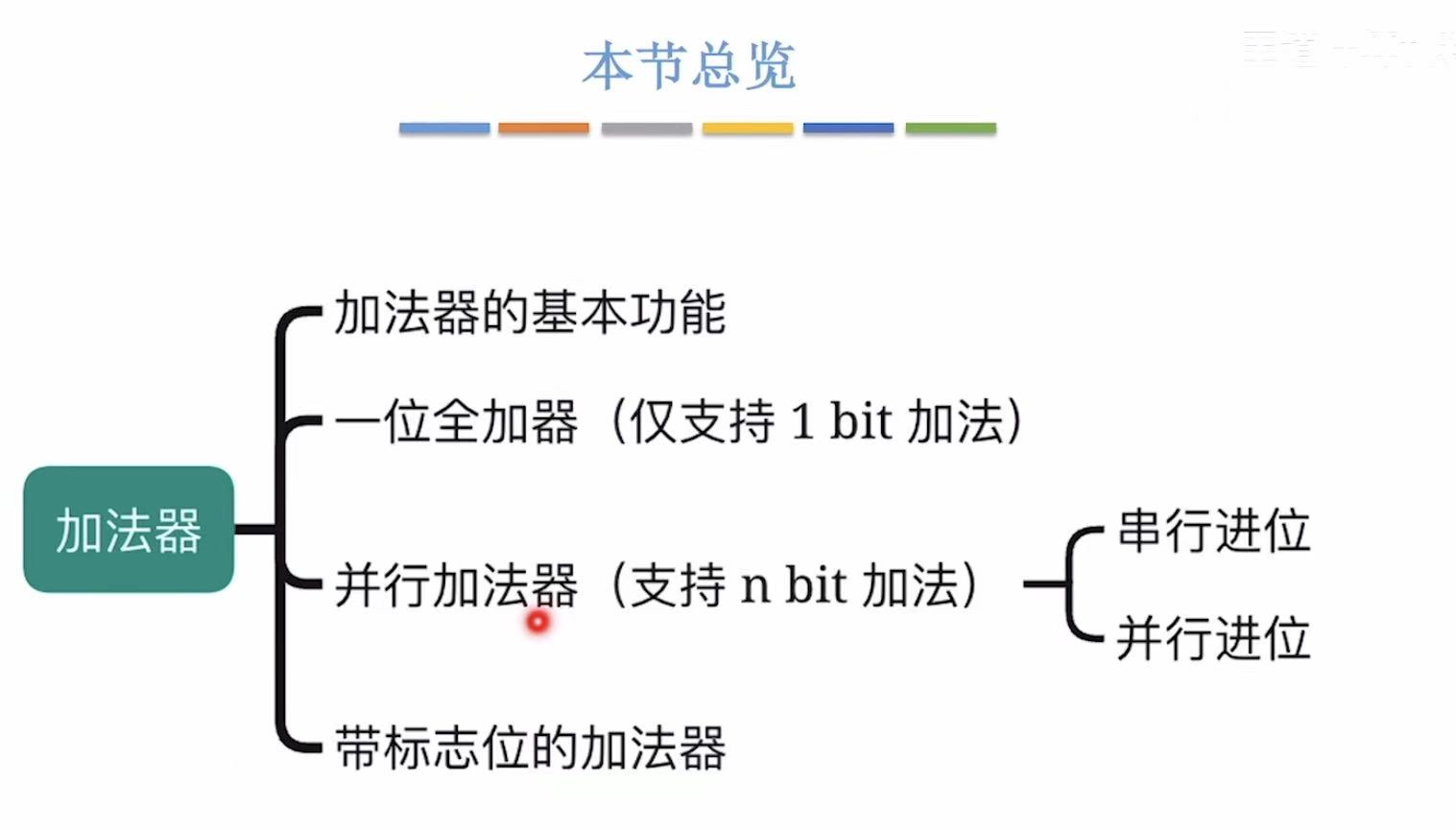
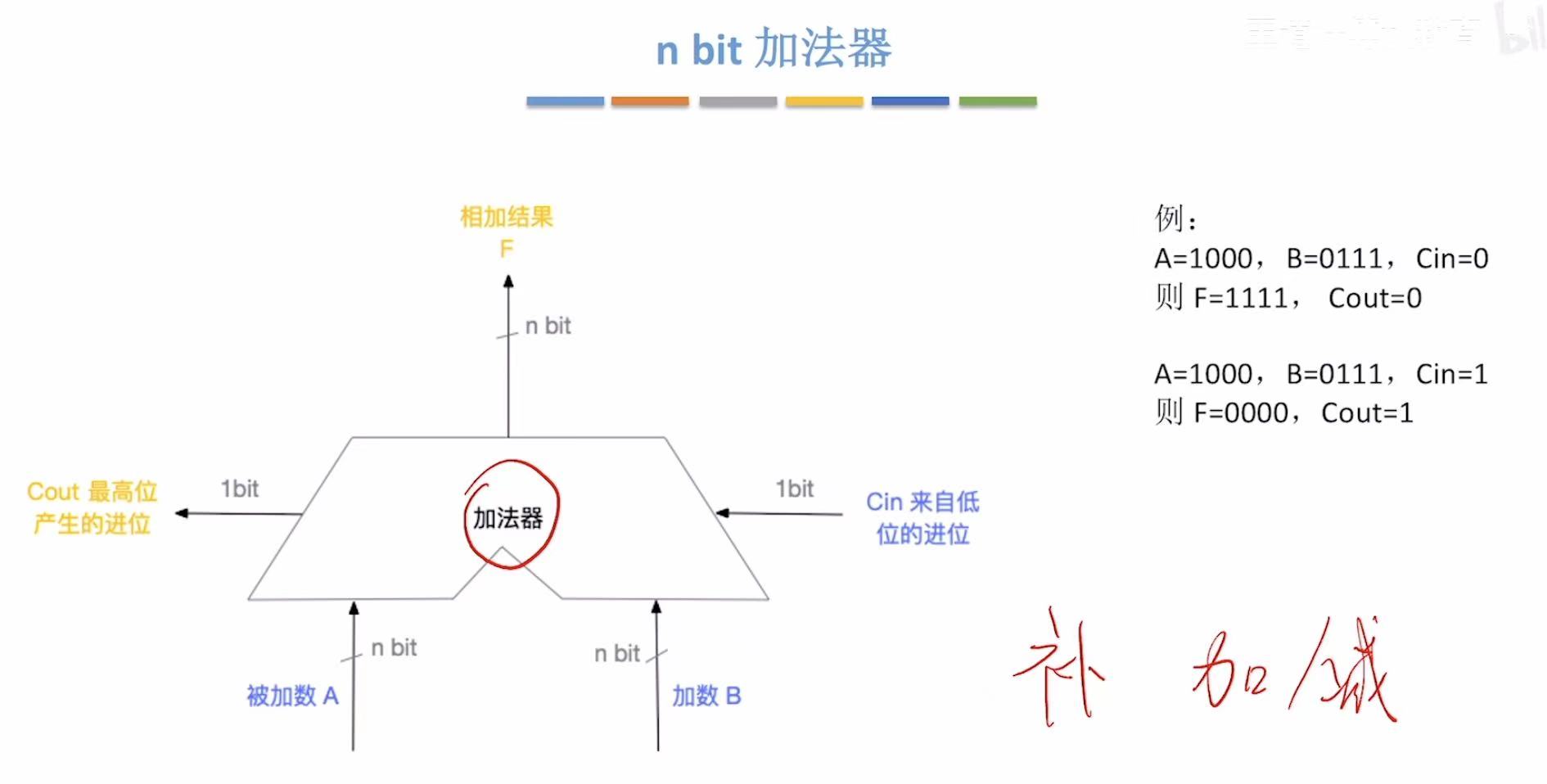
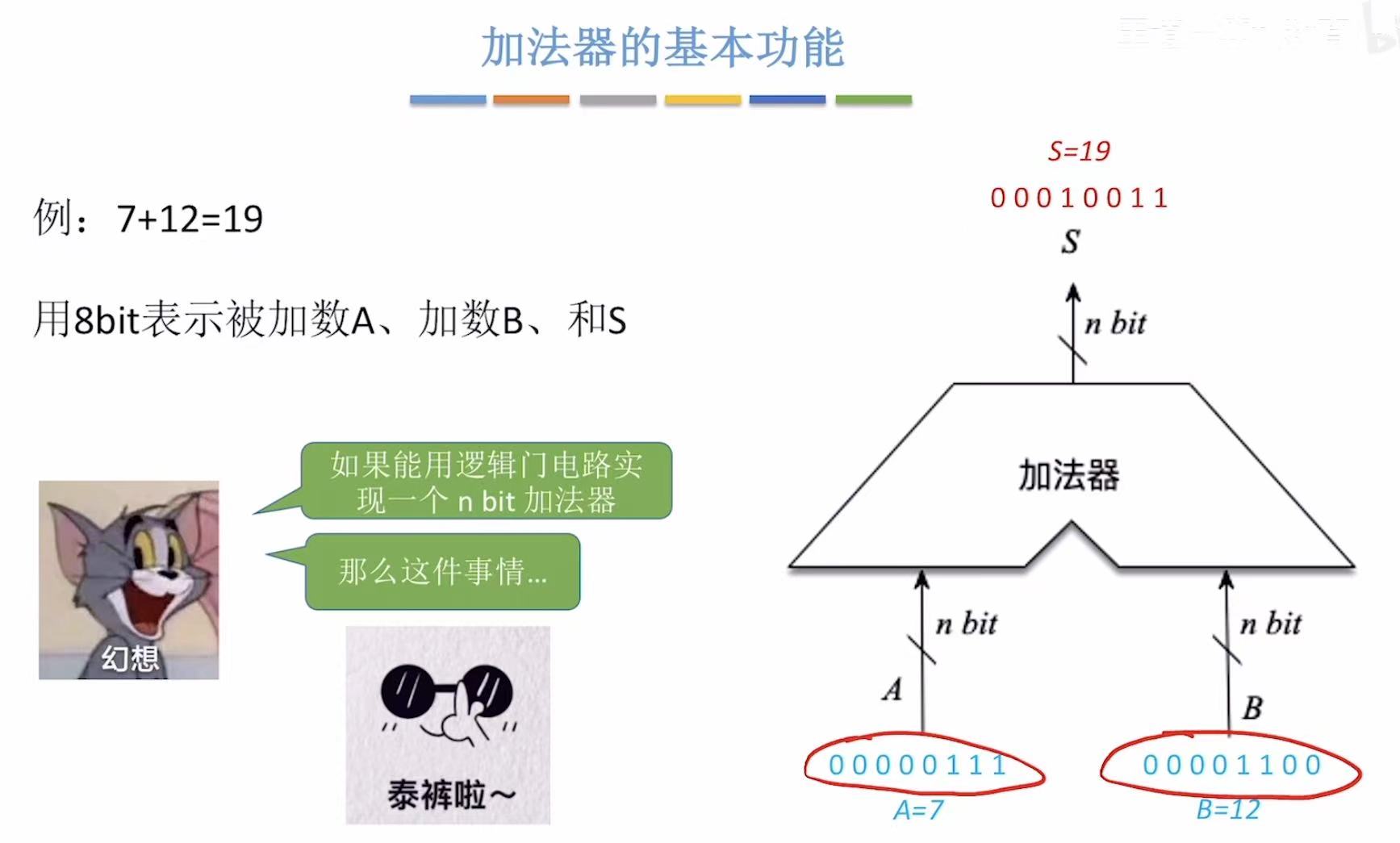
1. 加法器的基本功能
本质就是输入两个数，输出一个数 。
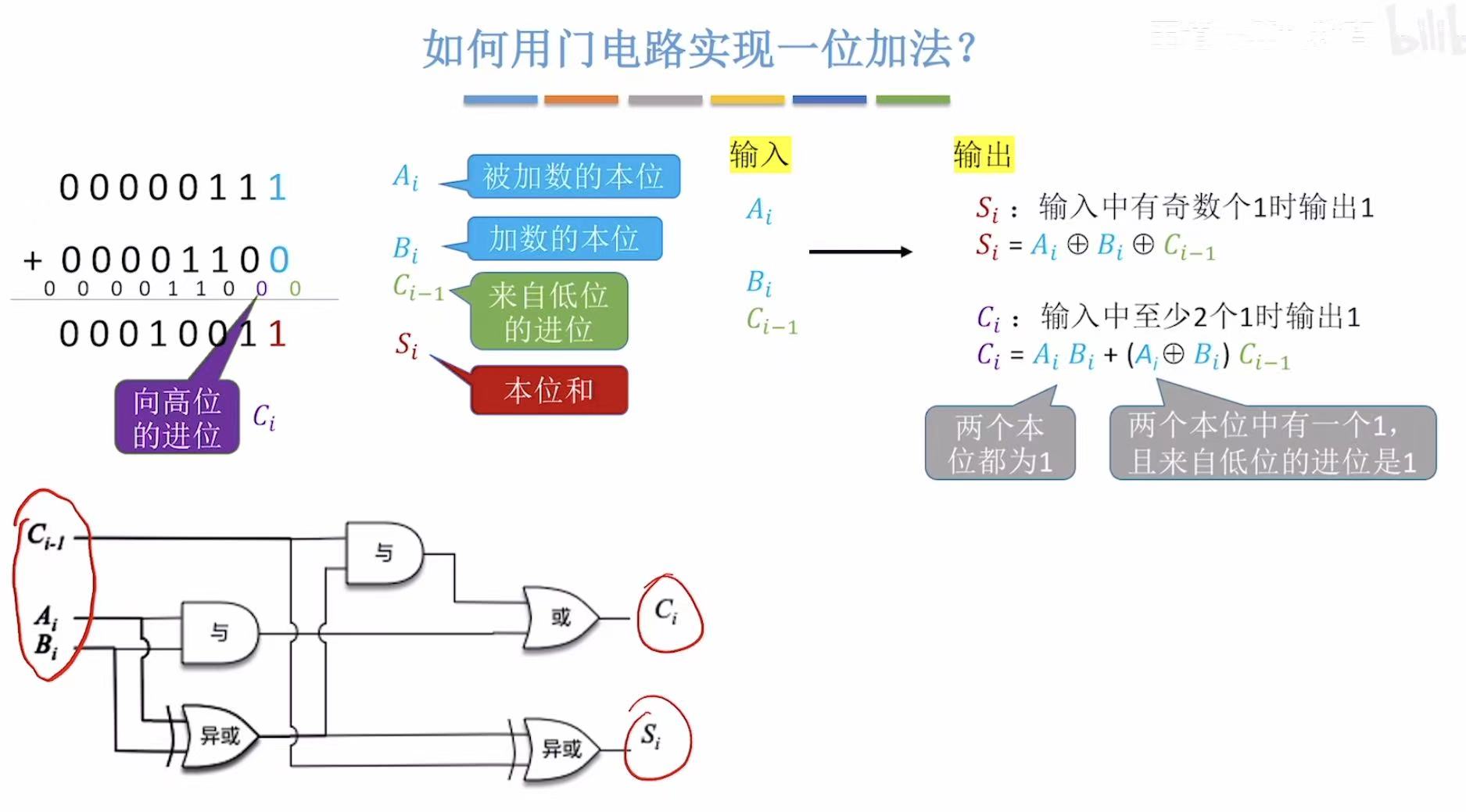
2. 一位全加器
引入了进位，所以变为了输入三个数（外加低位进位），输出两个数（外加高位进位）。
然后我们需要考虑的就是怎么在这个机器内部用门电路 实现加法这个功能。（也就是设计电路-->硬件 ）
是的，门电路是用来设计硬件的√，所以有门电路的时候，就可以视为设计硬件，从更形象的角度理解我们为什么需要这样设计。（也就是要节约硬件资源，或者是神马其他的...）
因为一位一位往后算，所以叫一位全加器。
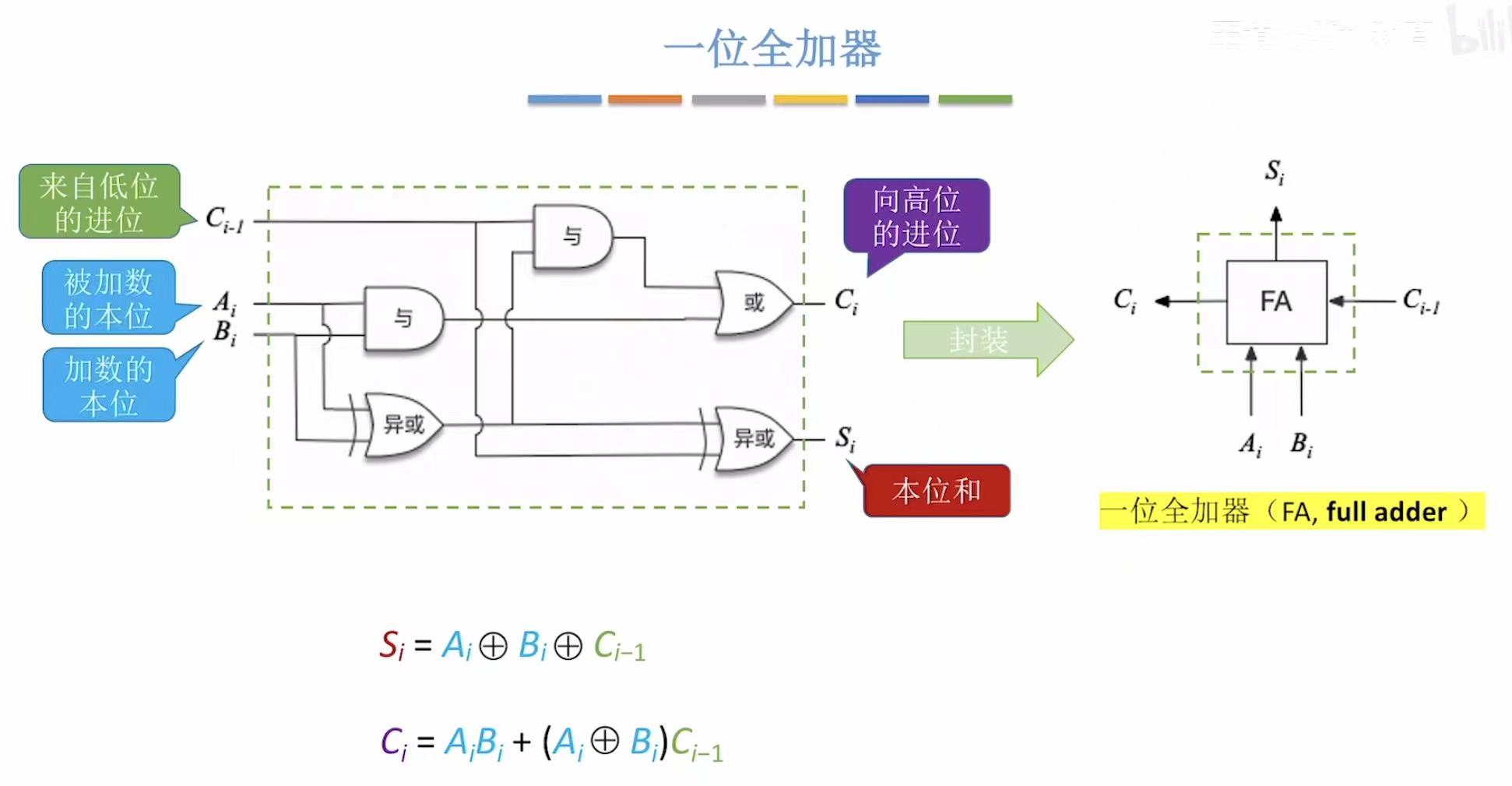
3. n bit加法器
就是n个一位全加器串起来，嗯，n*1=n，很合理。
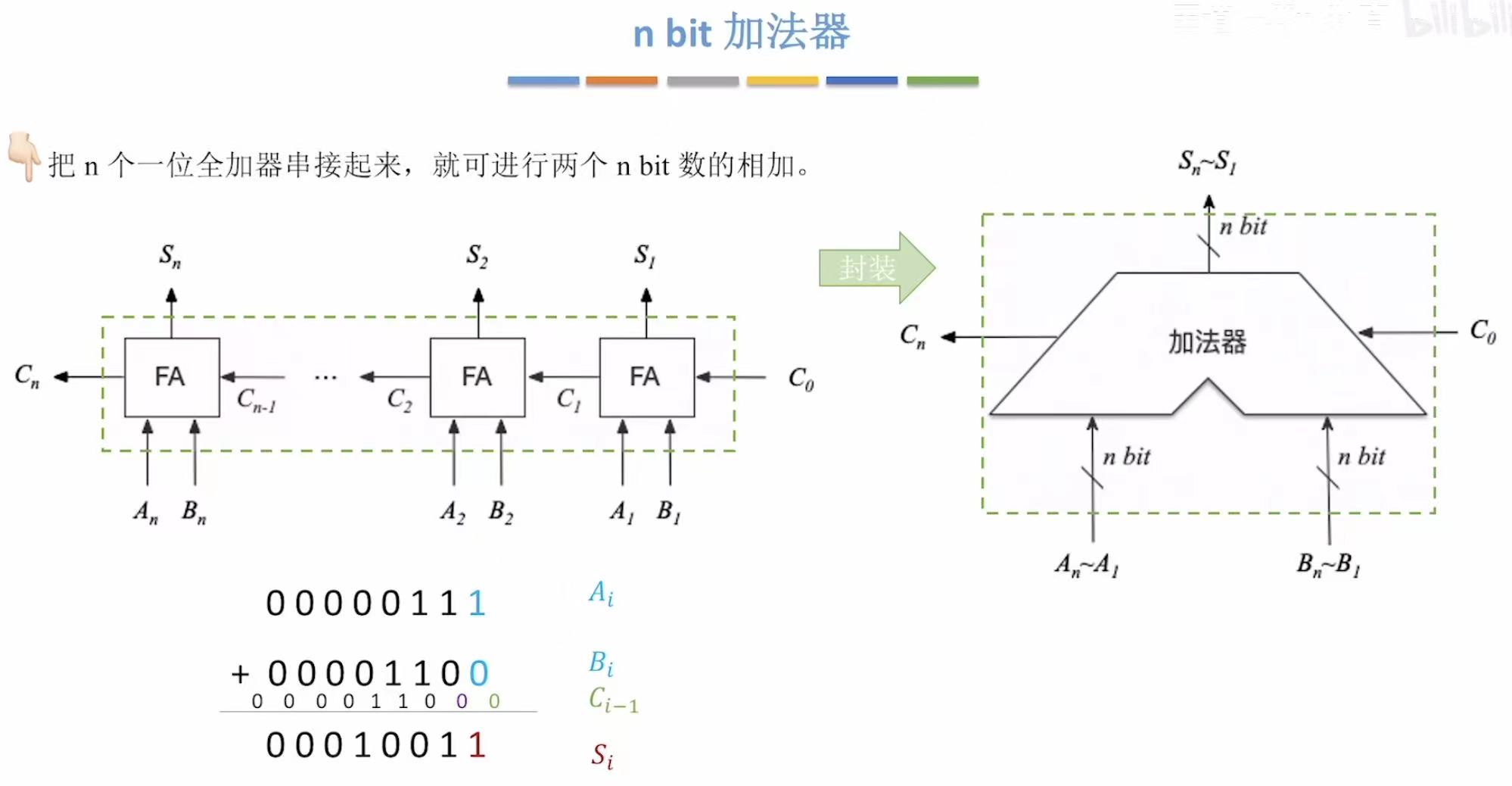
串行的就是算完这个然后才能往下算，所以数字很长的时候算的就慢。
注意加法器因为可以同时输入数字，所以叫并行加法器，这个是串了好几个的并行加法器，所以叫串行进位 的并行加法器，
下一小节的是并行进位 的并行加法器，区别 是串行是挨个儿算的，并行是同时算的。
区别：在于进位！！！！！
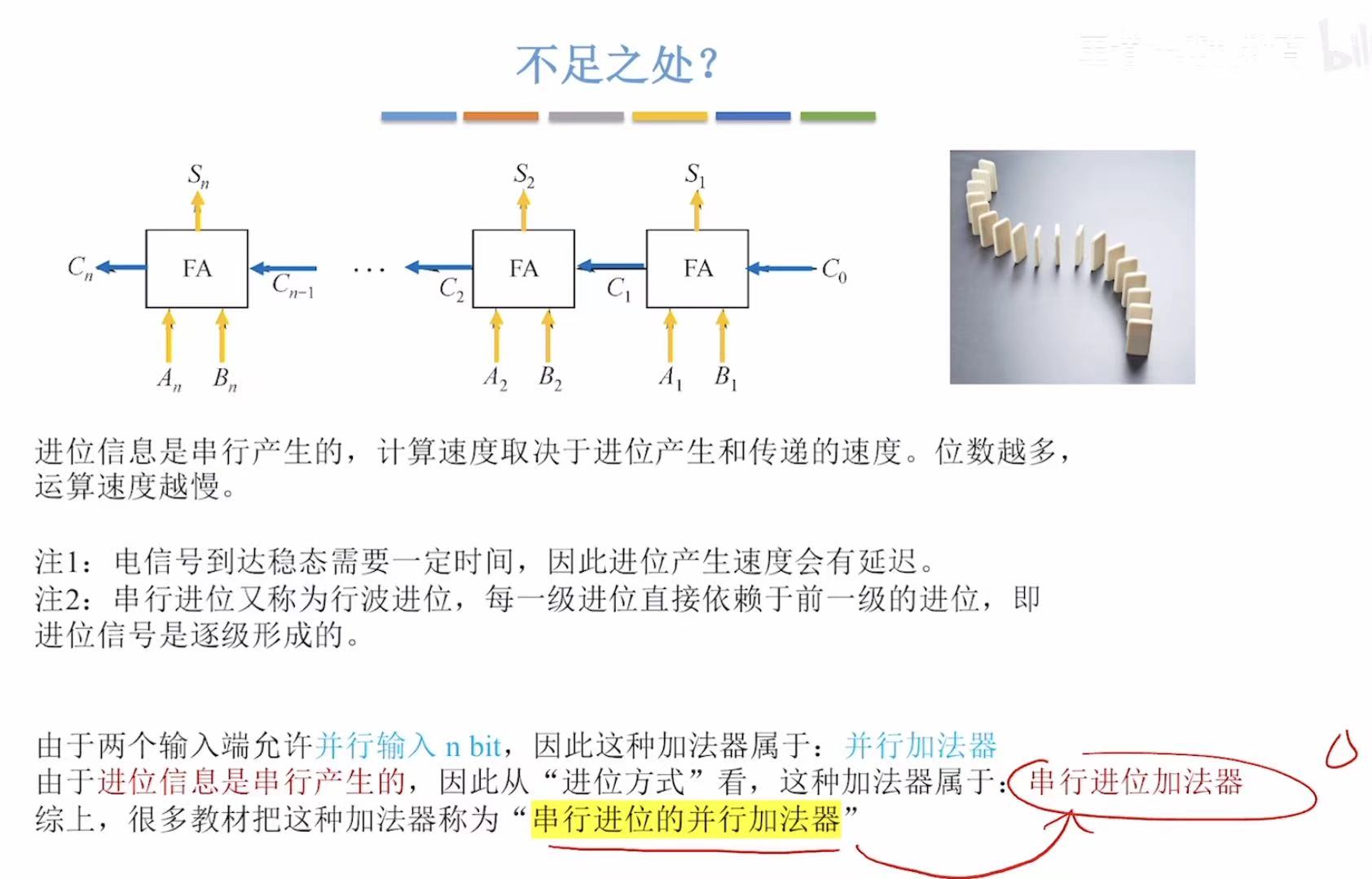
4. 并行加法器
可以同时算，得到进位信息。
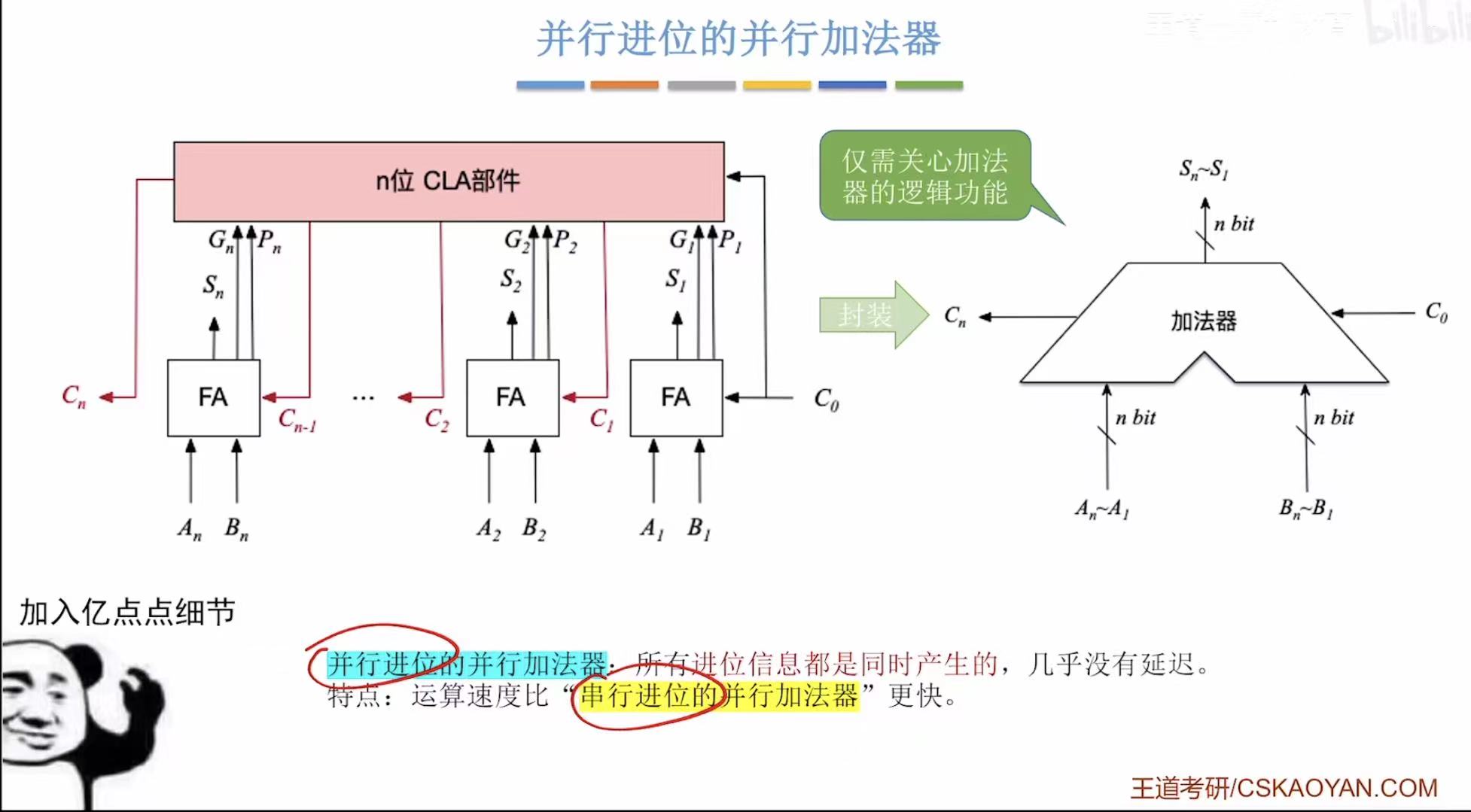
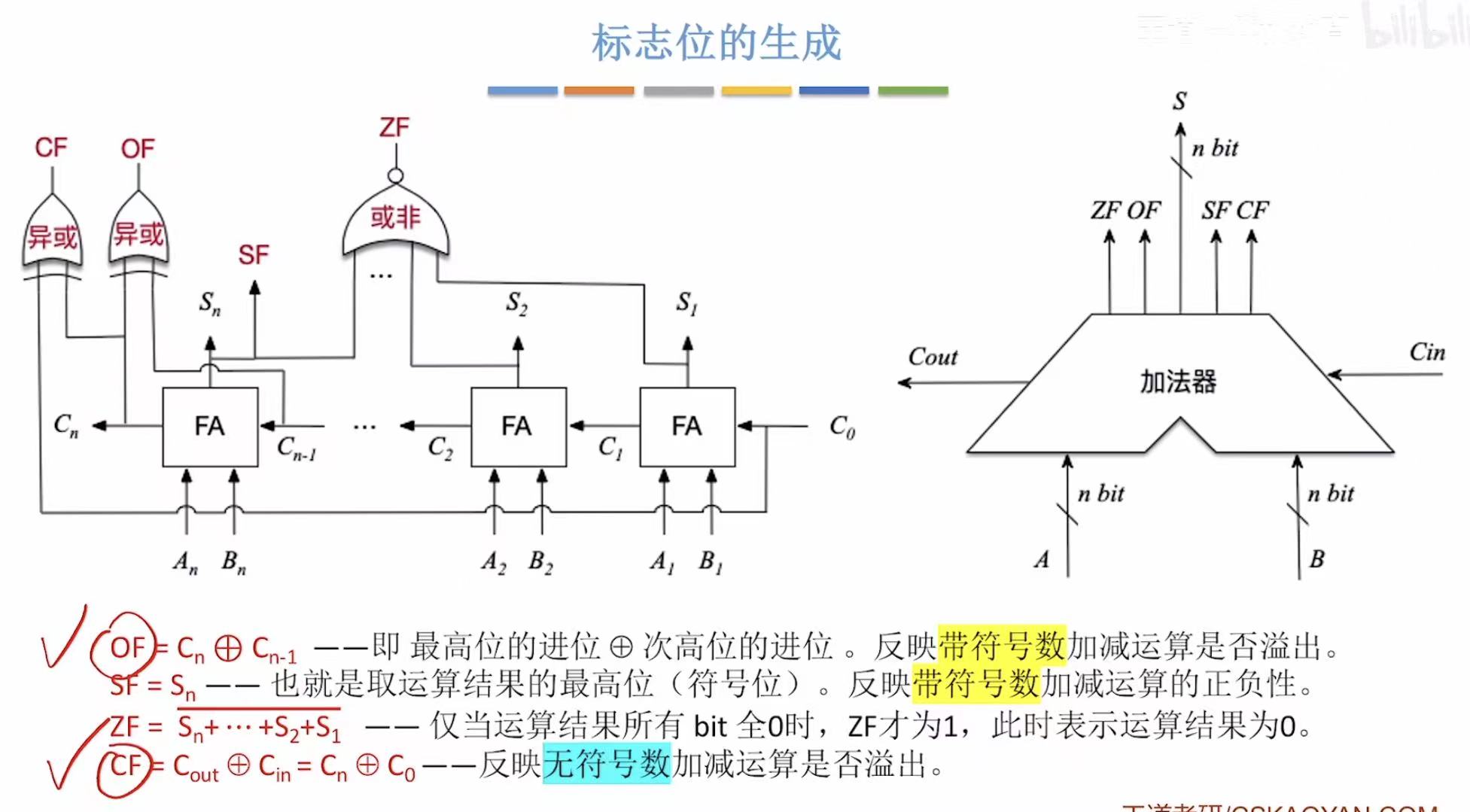
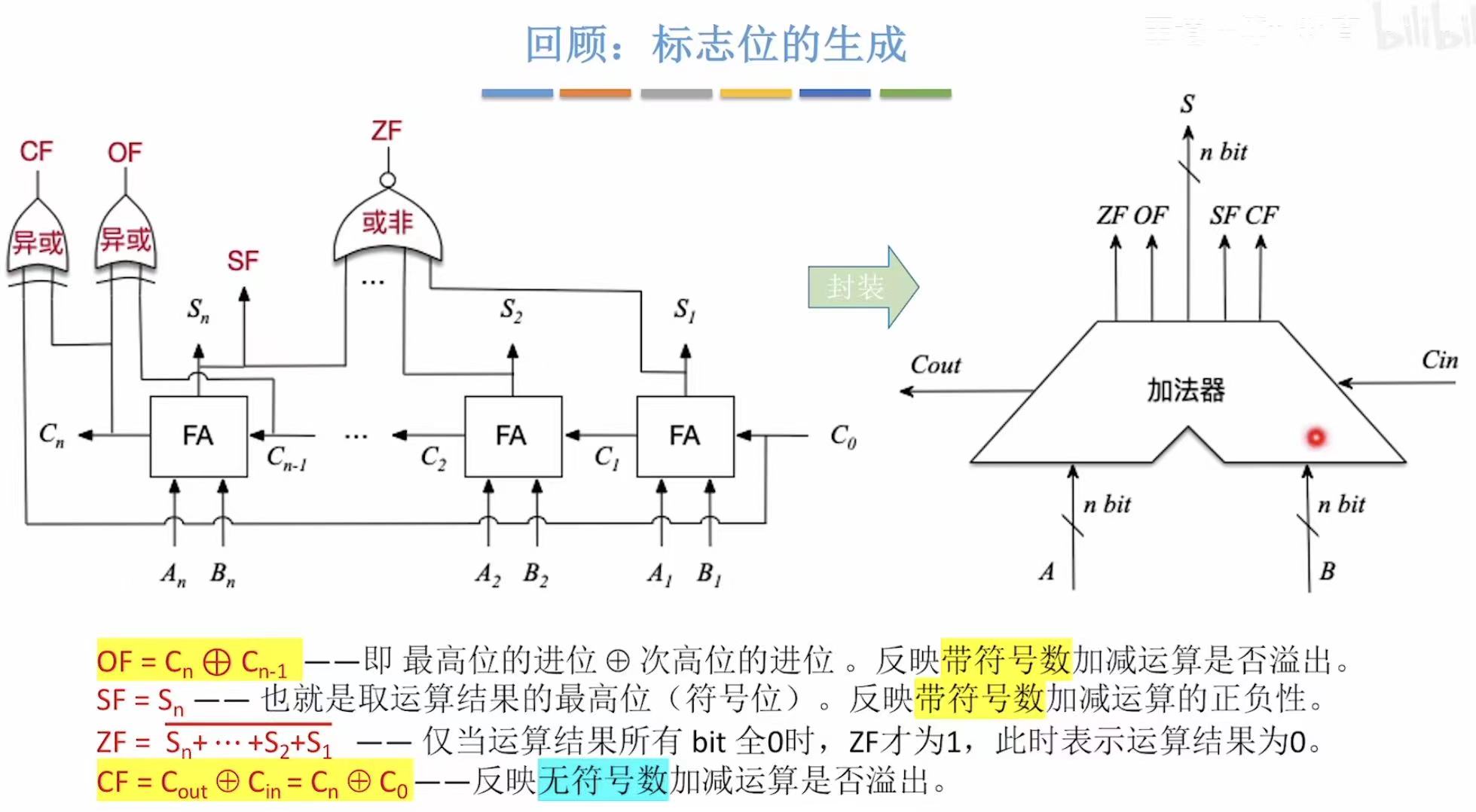
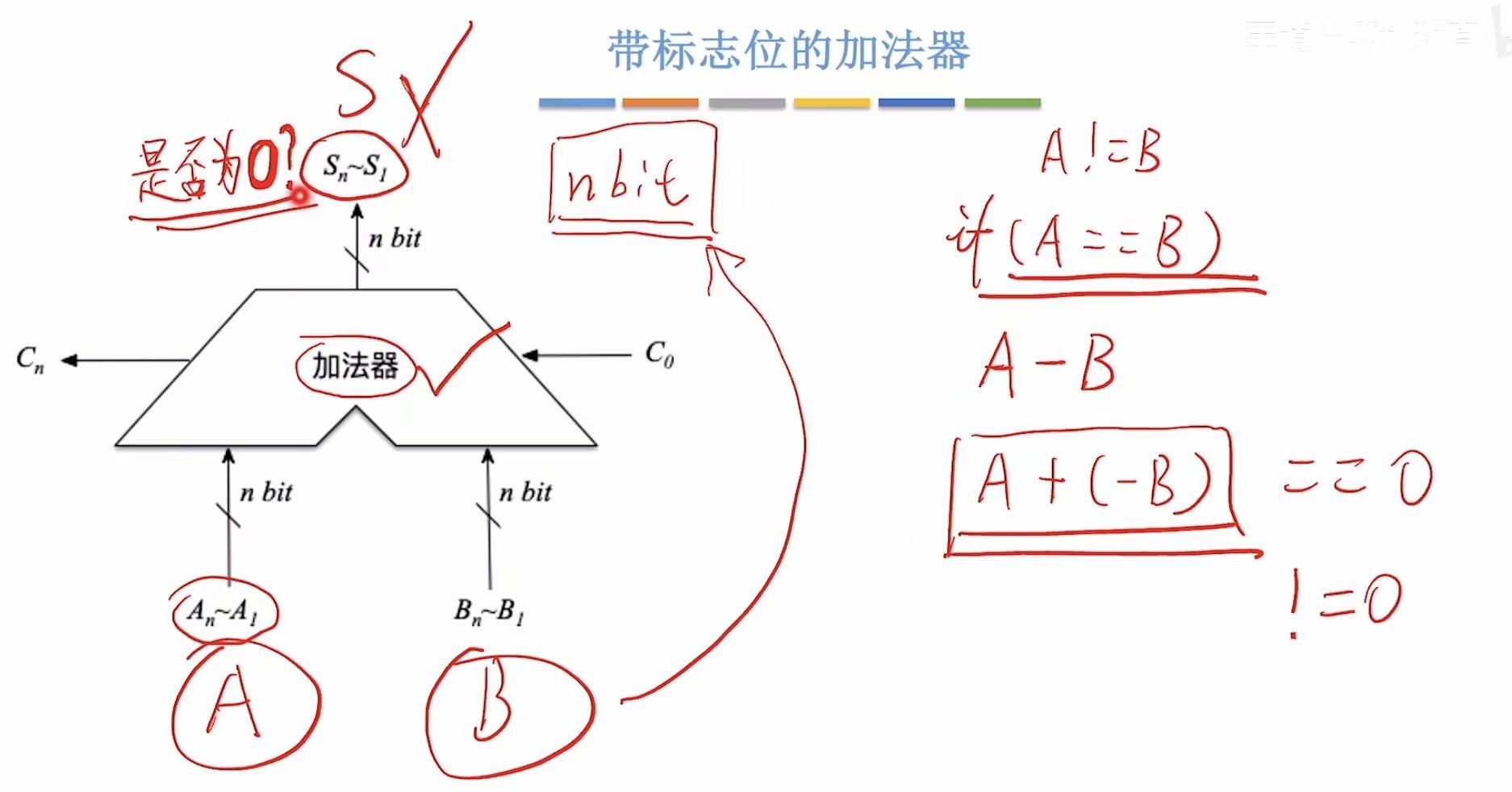
5. 带标志位的加法器
可以通过查看结果是否为0来判断结果是否正确。
通过查看是否溢出来判断结果是否正确。
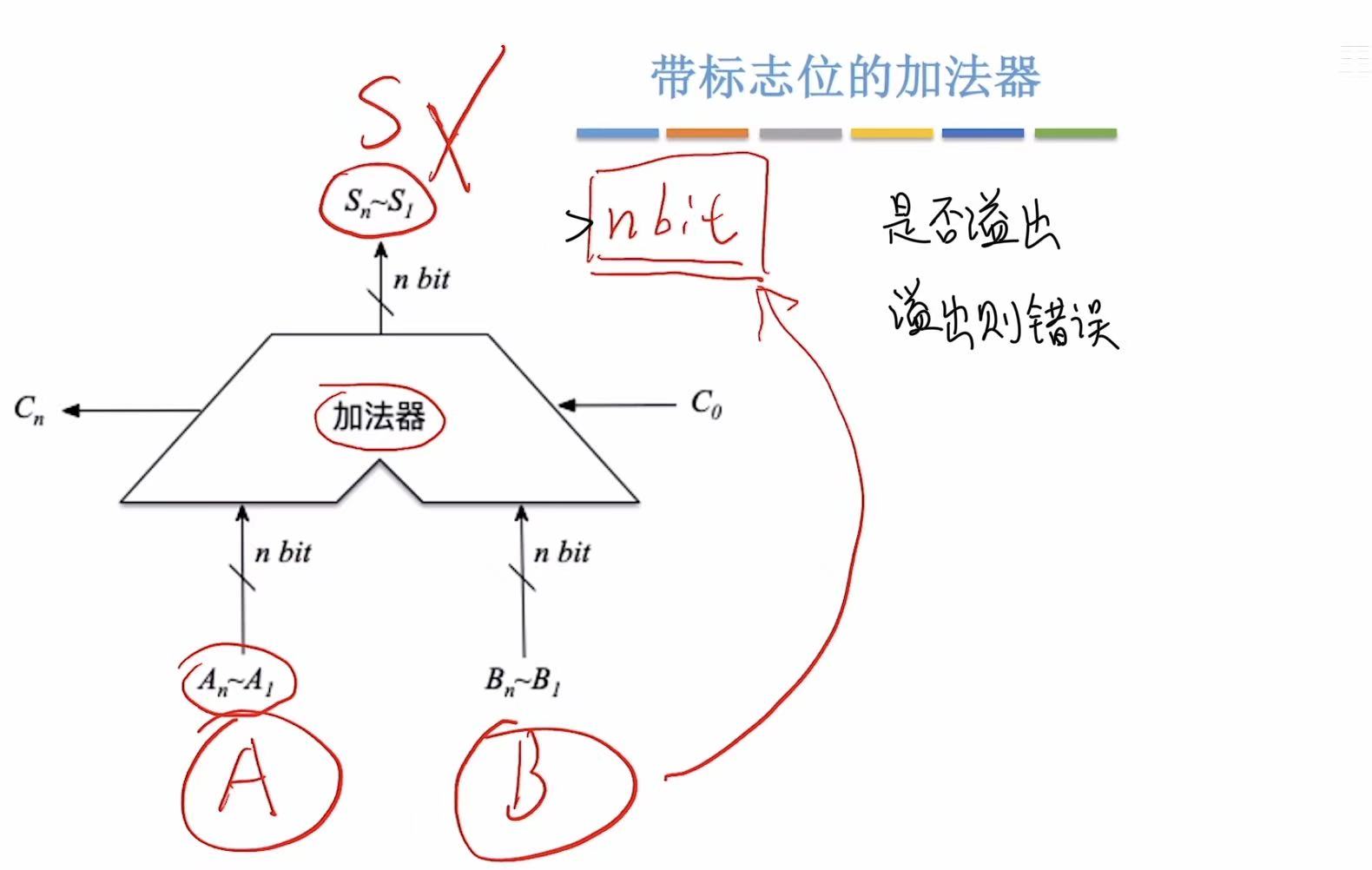
通过查看结果的正负来判断结果是否正确。
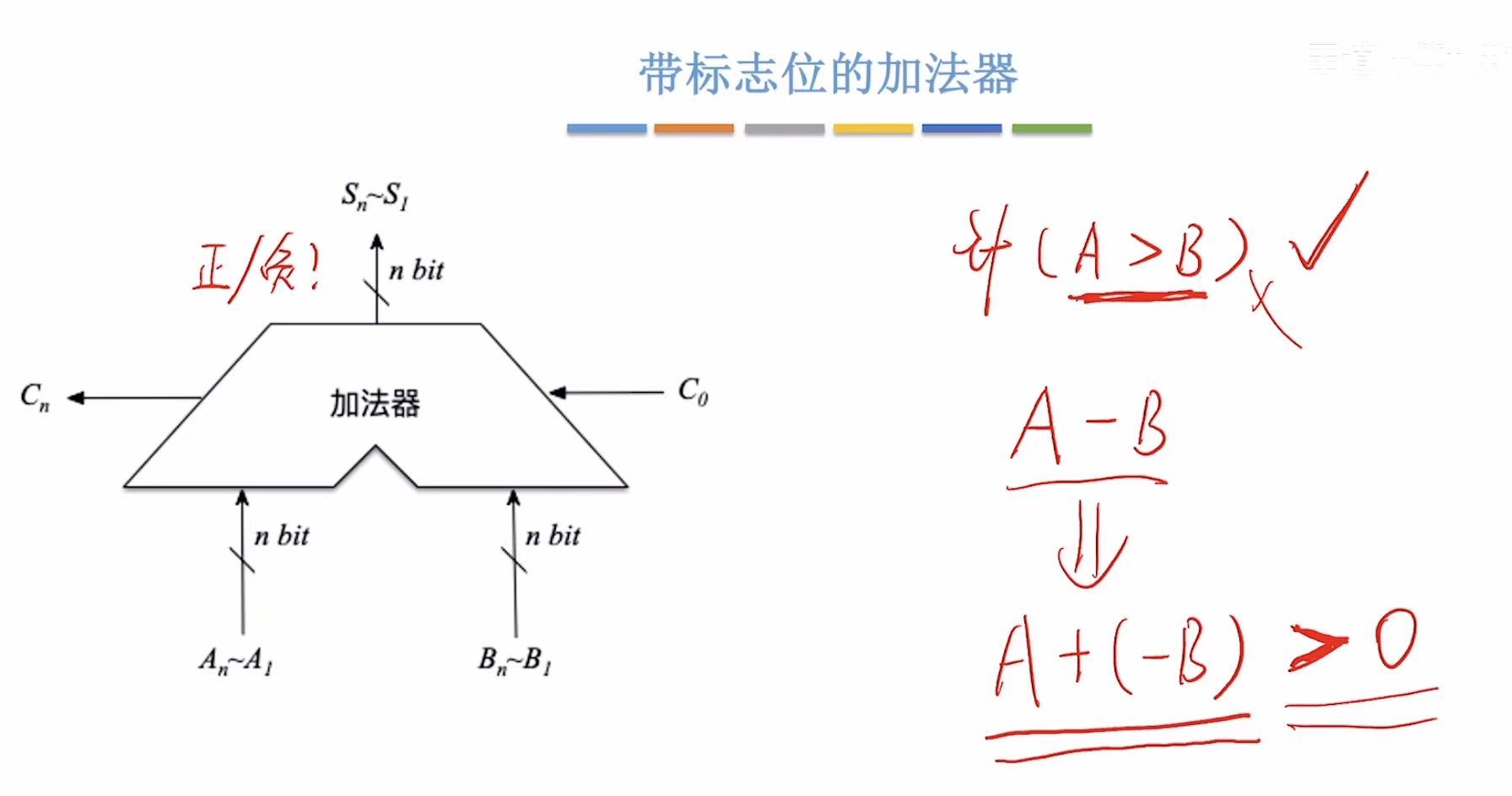
因为上面三种情况可以用来判断结果的正确与否，所以引入了标志位，通过标志来判断结果是否正确。
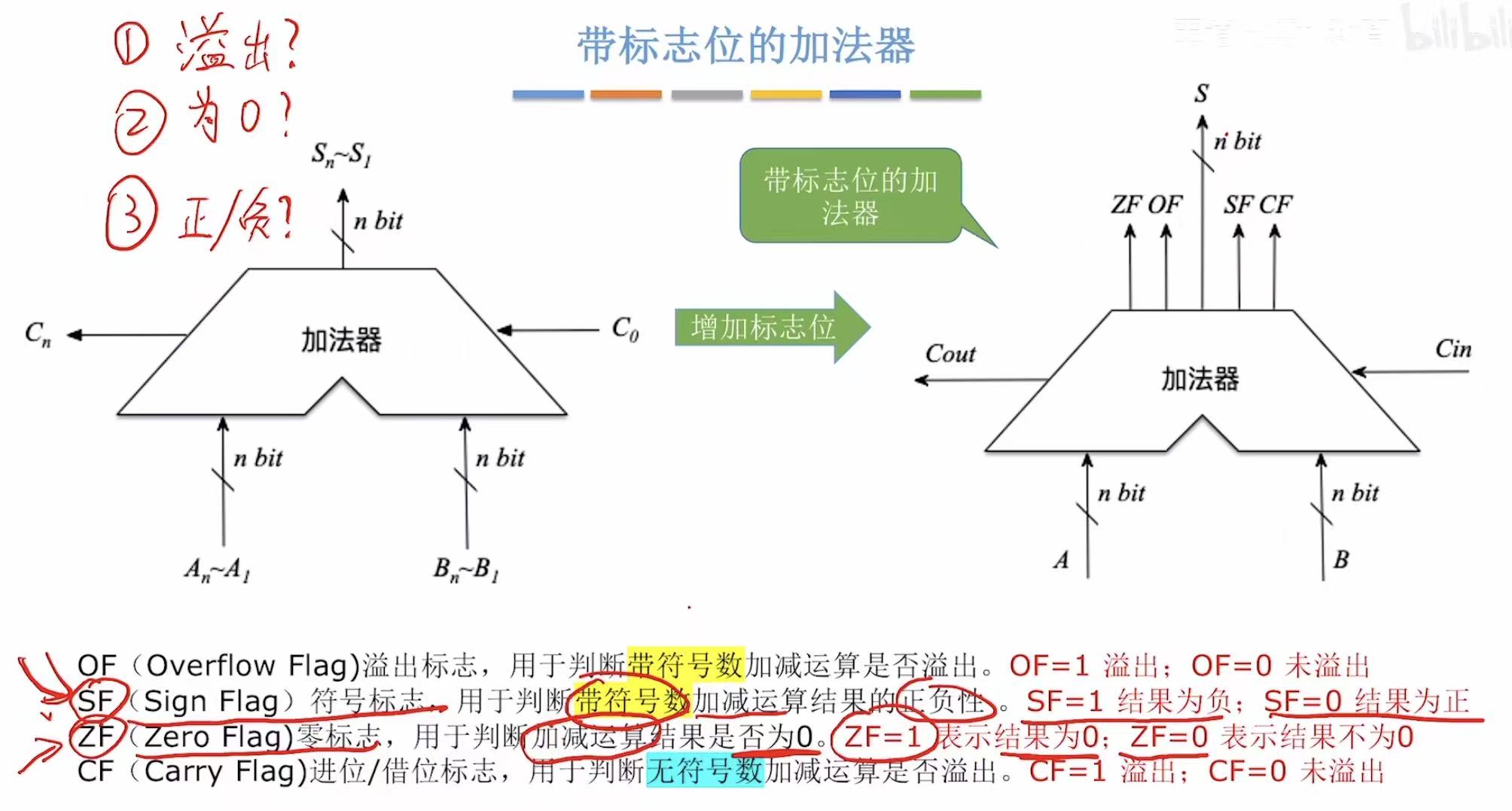
标志位的生成
6. 小结
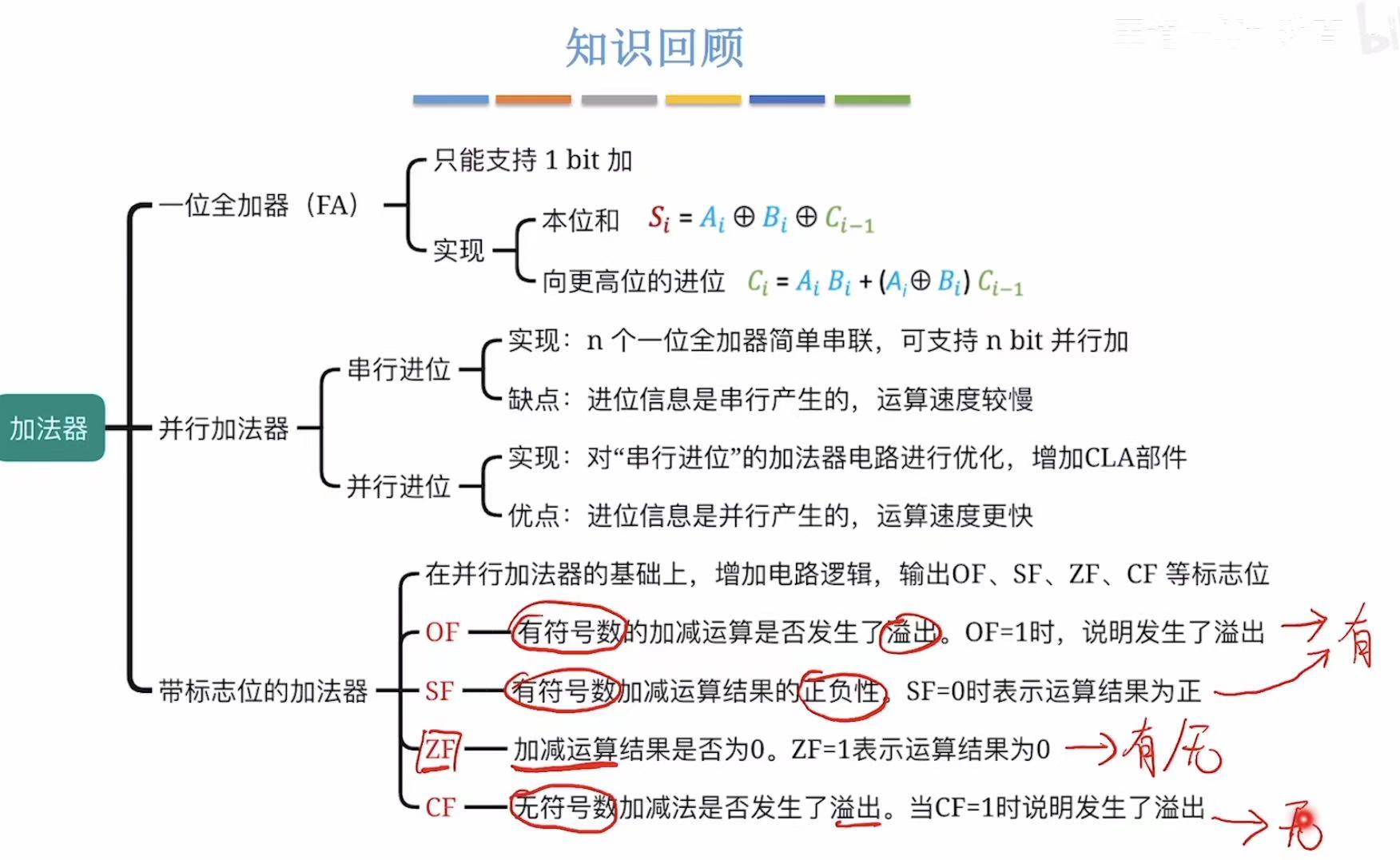
算术逻辑单位ALU
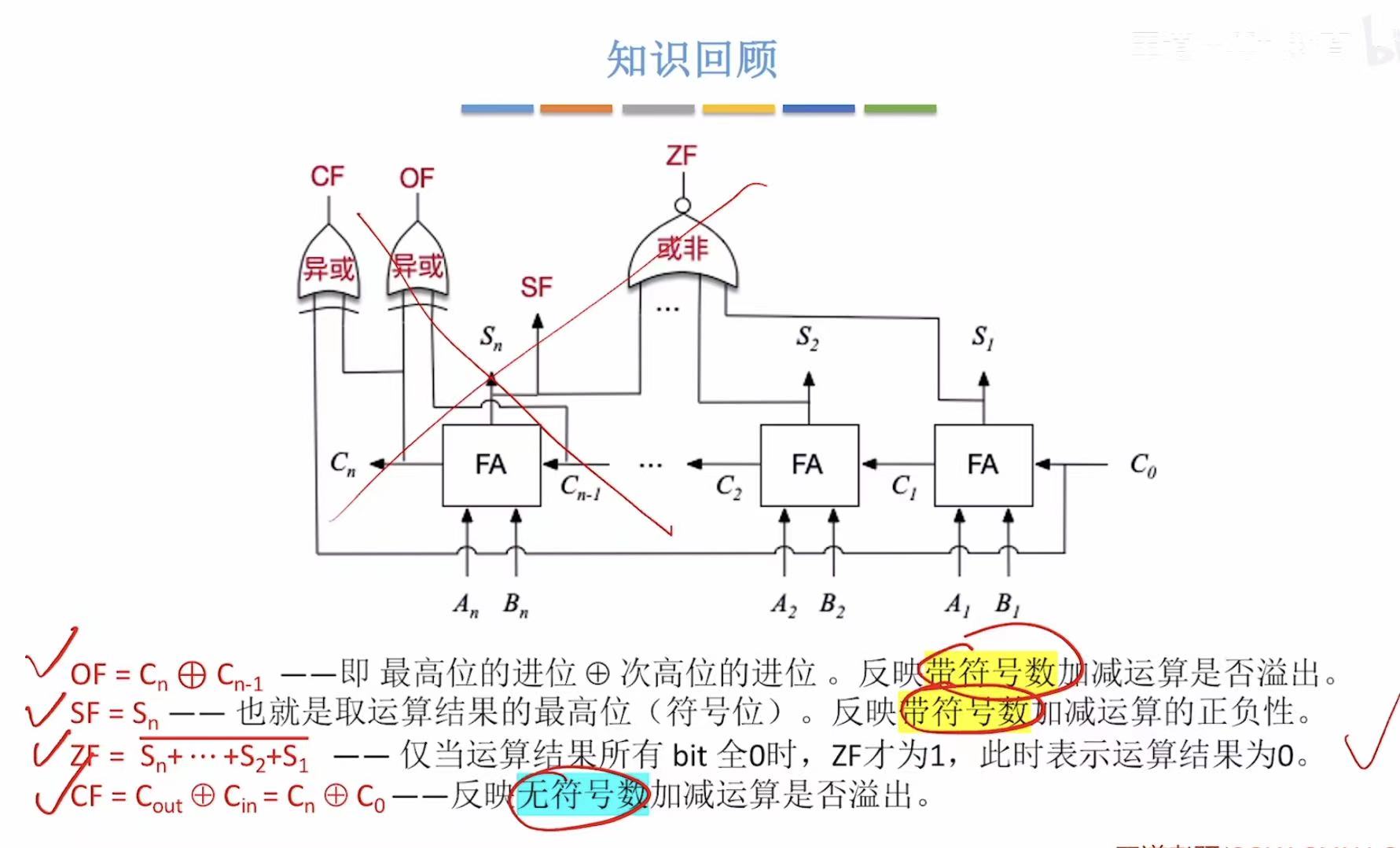
1. 作用
简单理解，就是一个实现了加减乘除等基础运算的零件而已。
加法器是ALU的核心。（毕竟加法可以演变成其他的算法）
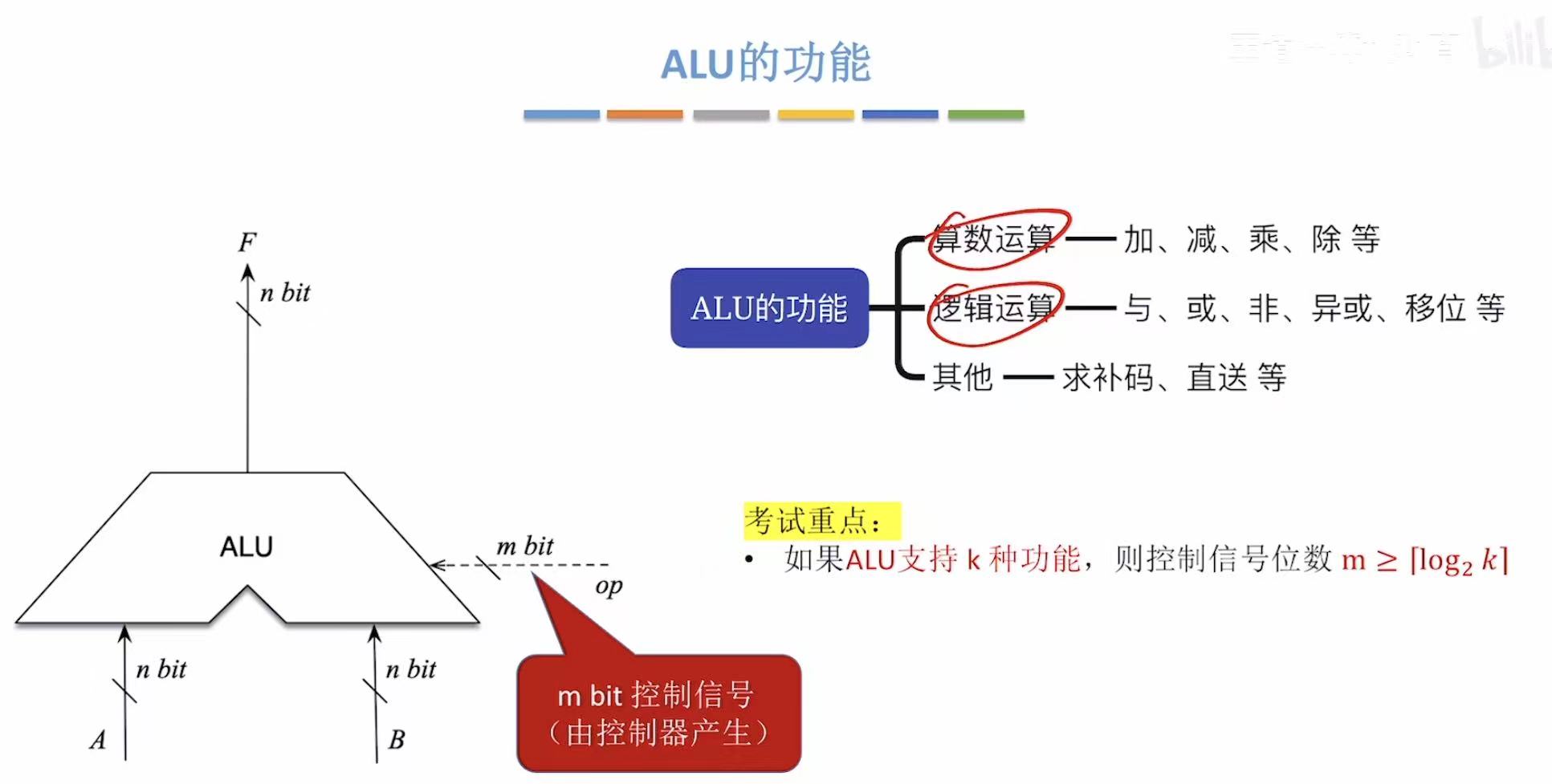
2. 功能
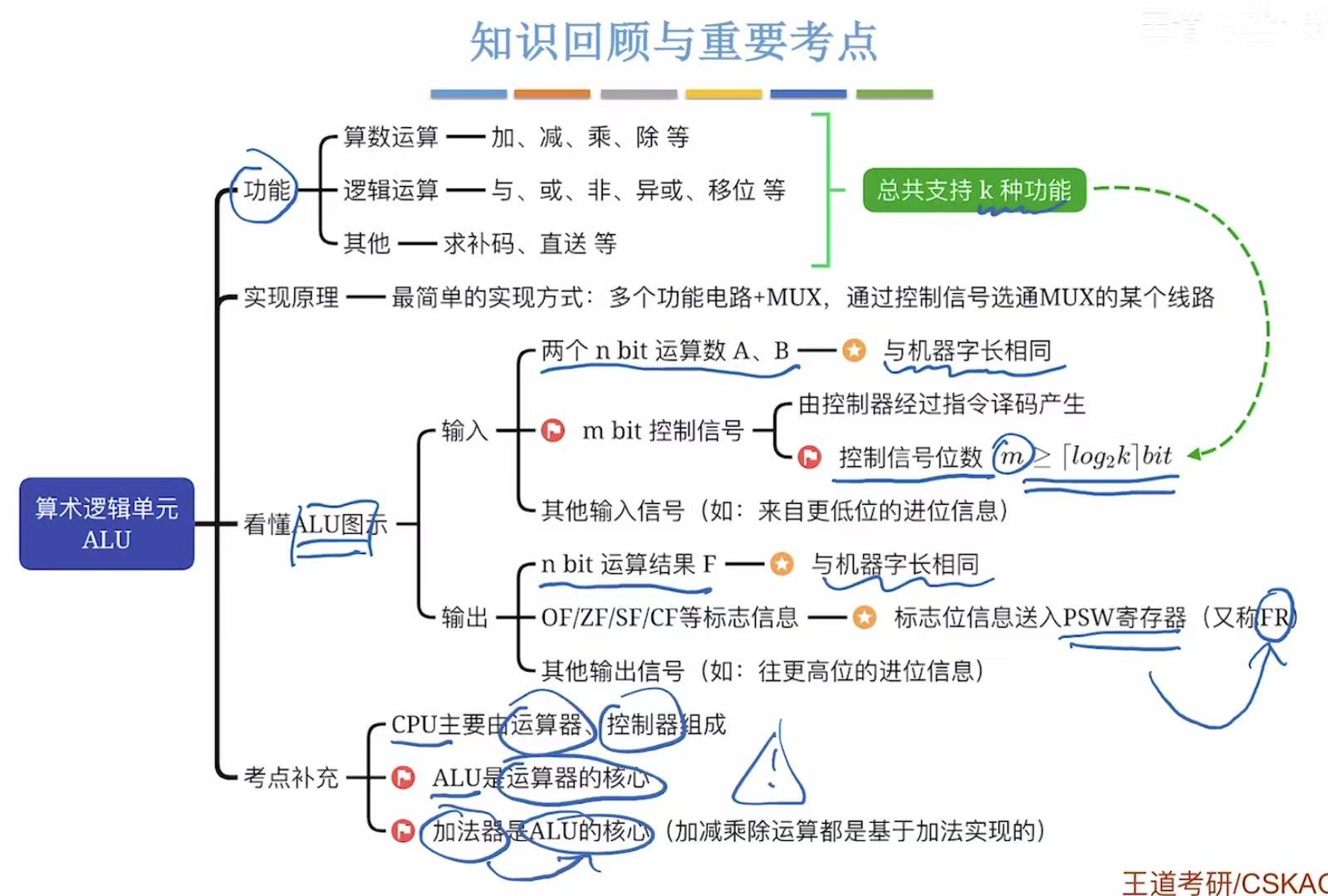
用哪个功能 （k），就按哪个按钮 （m）。
有几个功能（k），就要按照功能制造按钮（m）。
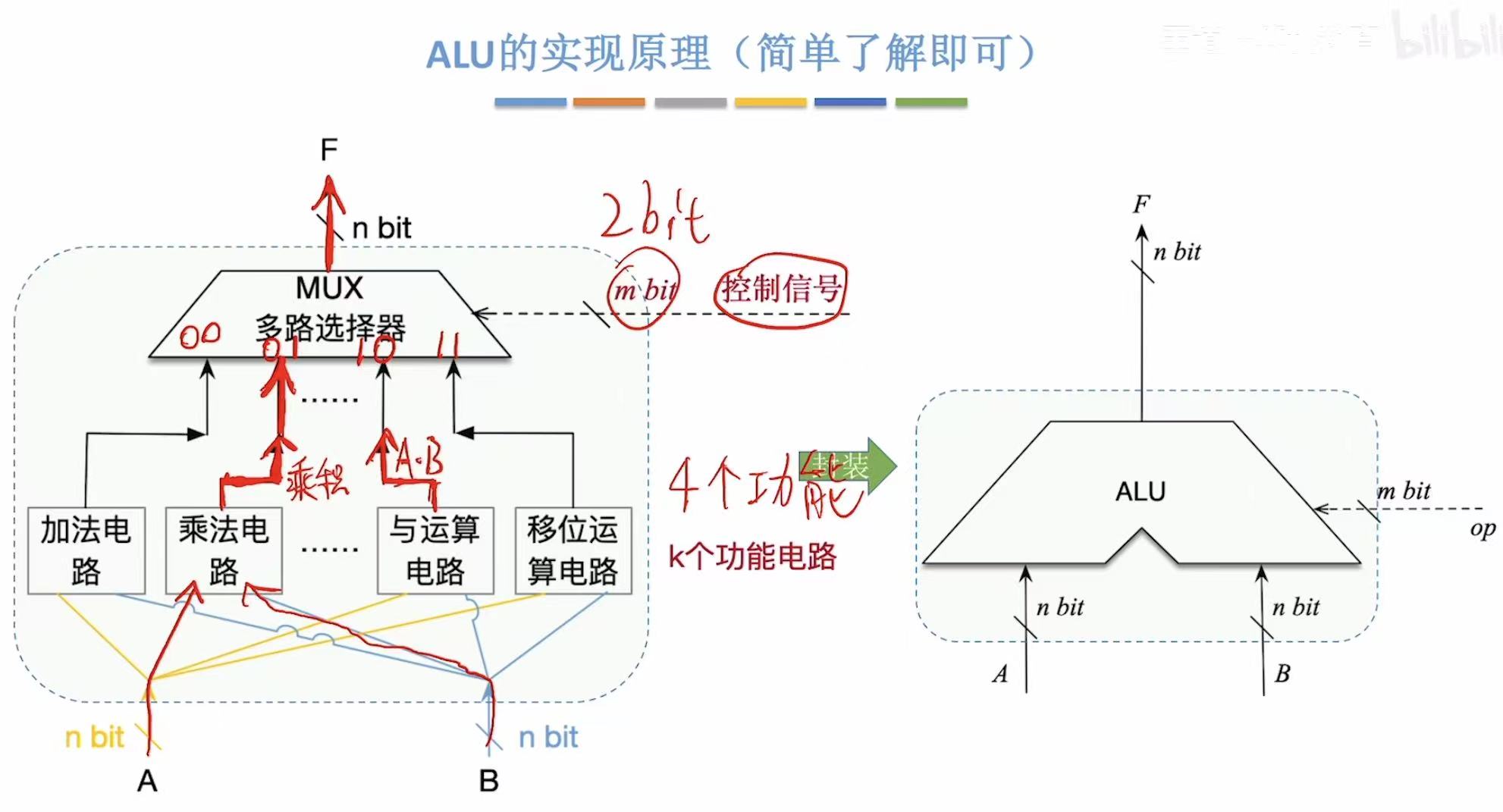
3. 实现原理（了解）
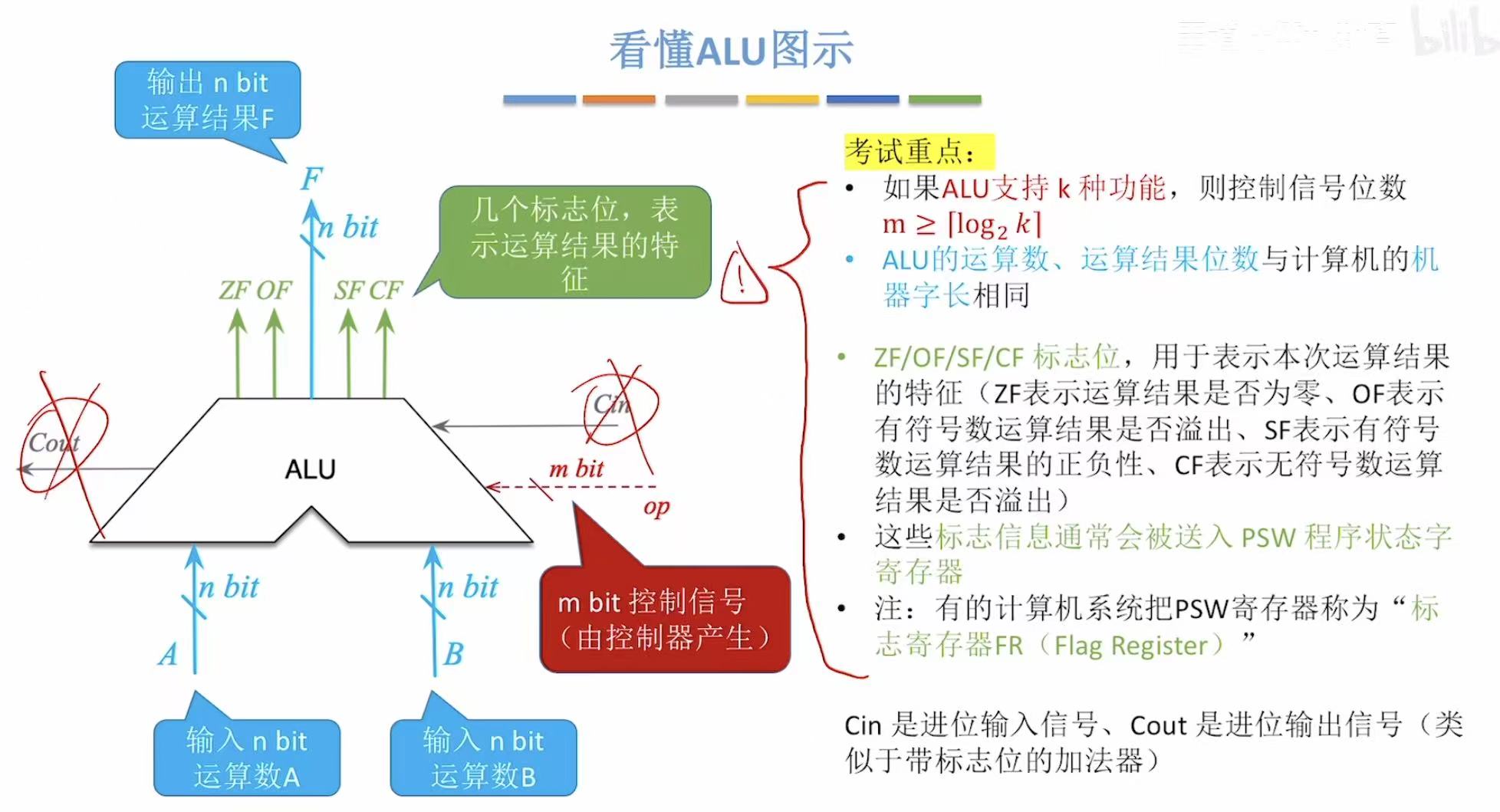
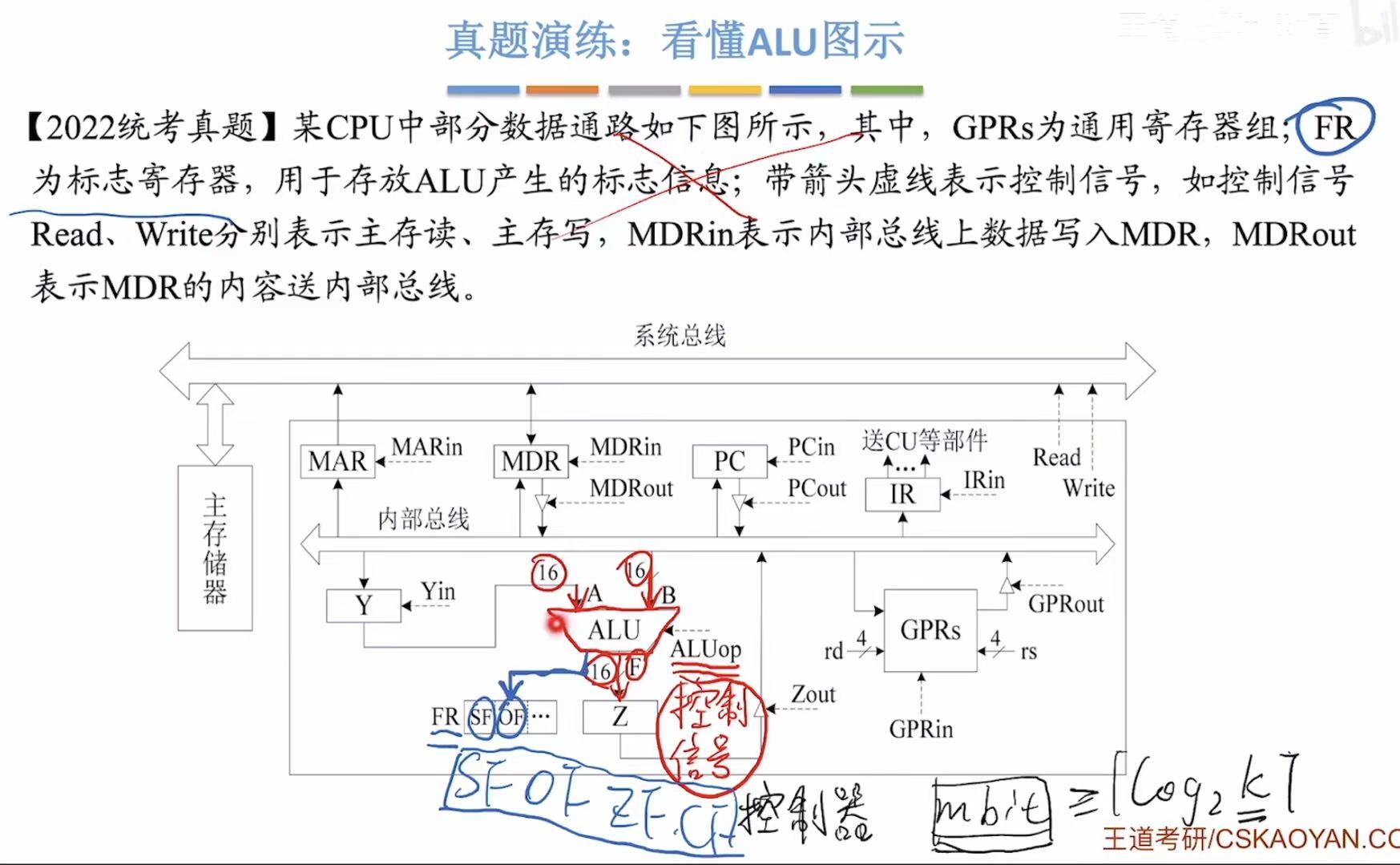
4. 看懂图示
看懂输入 、输出 和标志位 就差不多。
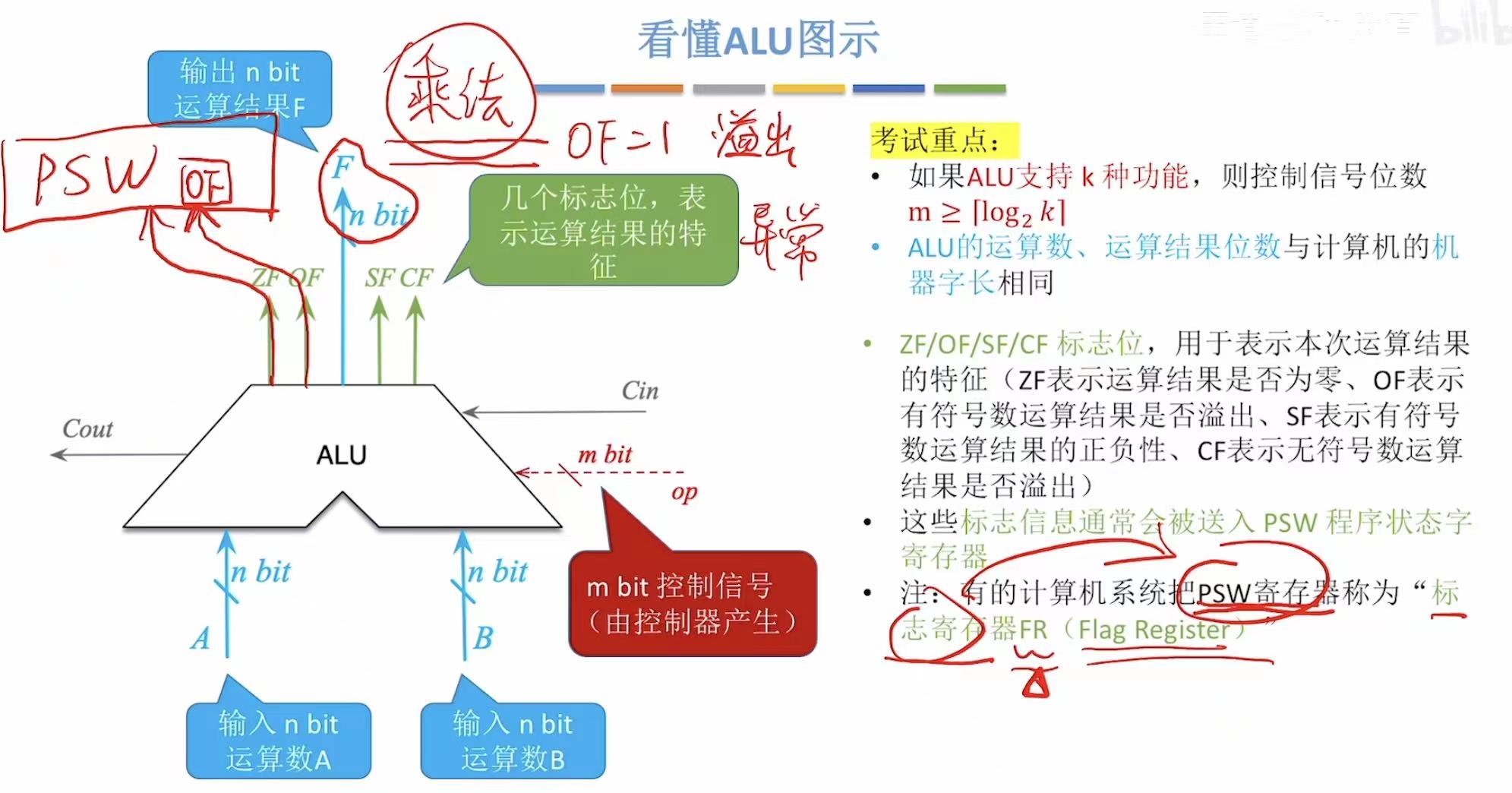
Cin和Cout不考。
5. 小结
定点数的移位运算
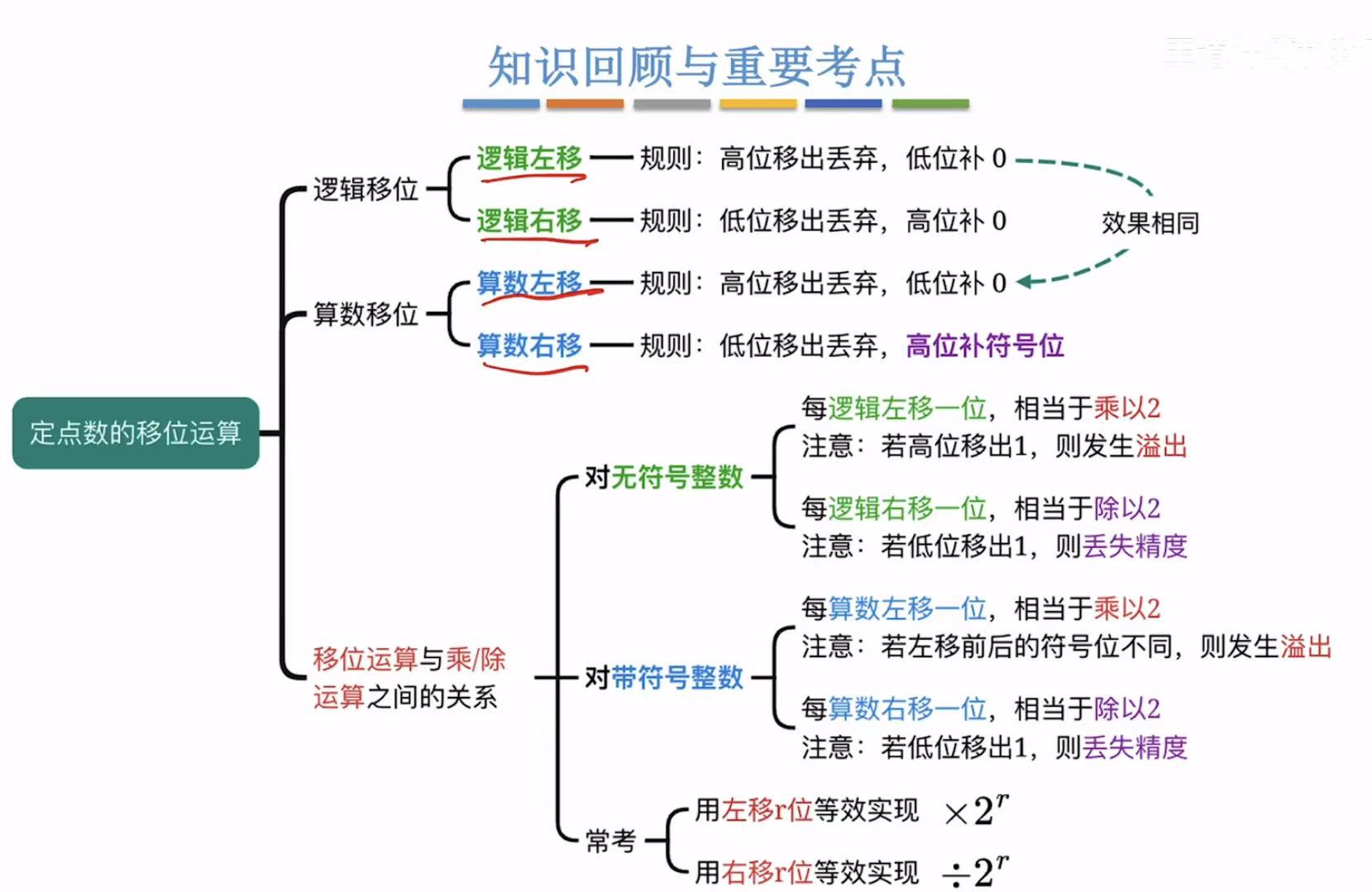
1. 逻辑移位（无符号）
因为是二进制的数，所以以2为倍数。
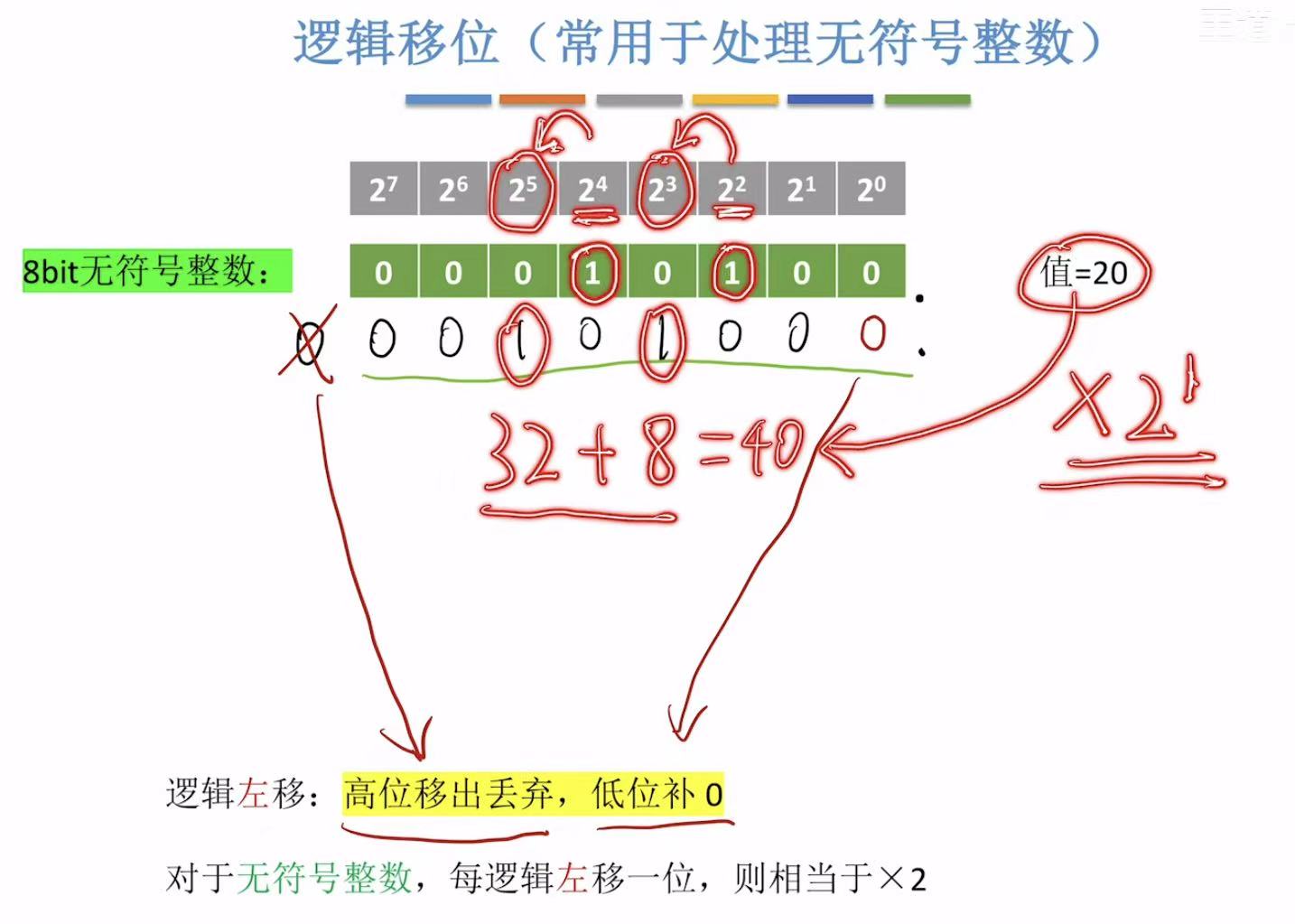
溢出 ：自己想要的数超出了它能表示的数字的范围。
比如：我想要的256>255，没办法用8比特的二进制数表示，所以就溢出了。
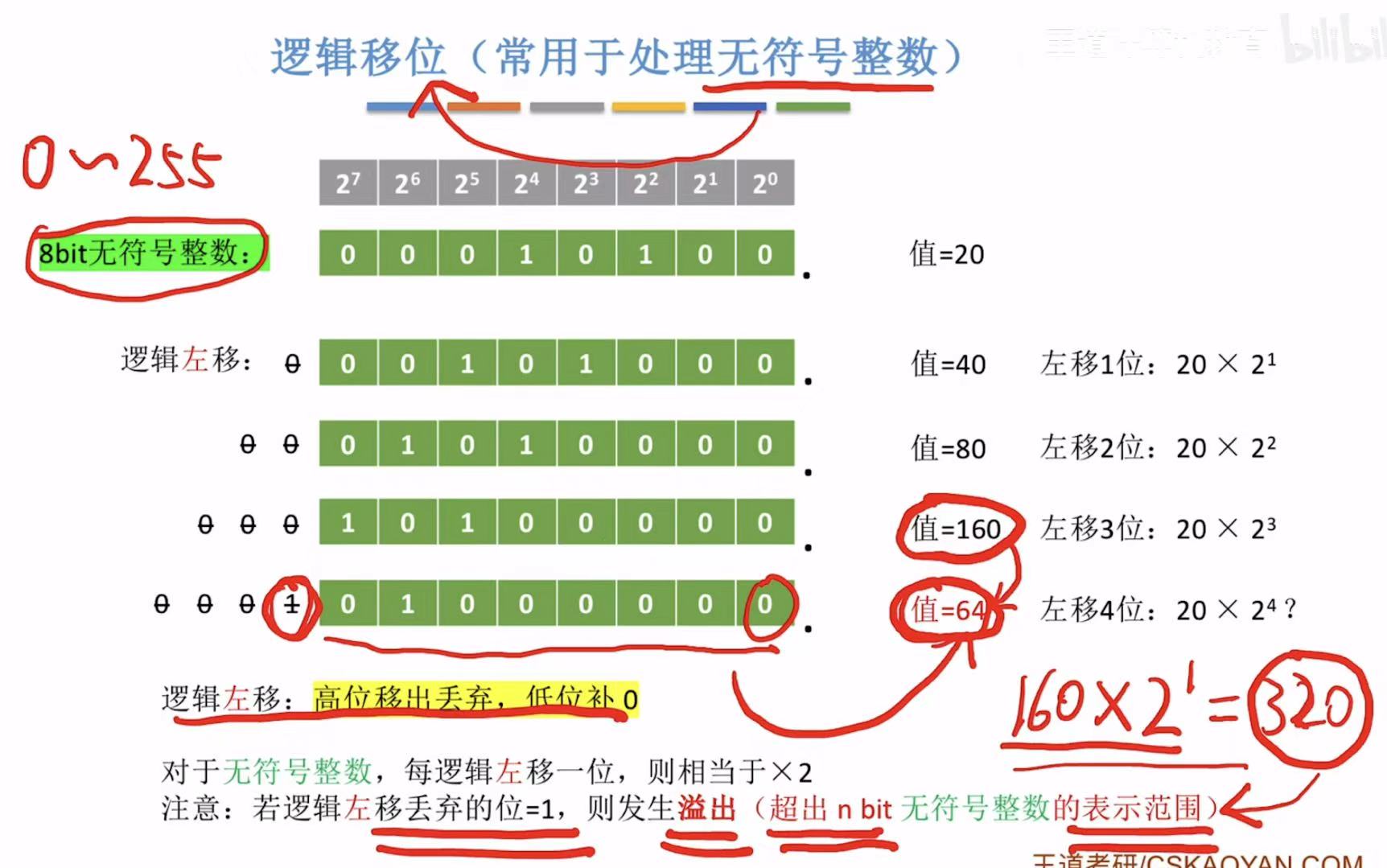左移：移出0-->无影响，移出1-->溢出；
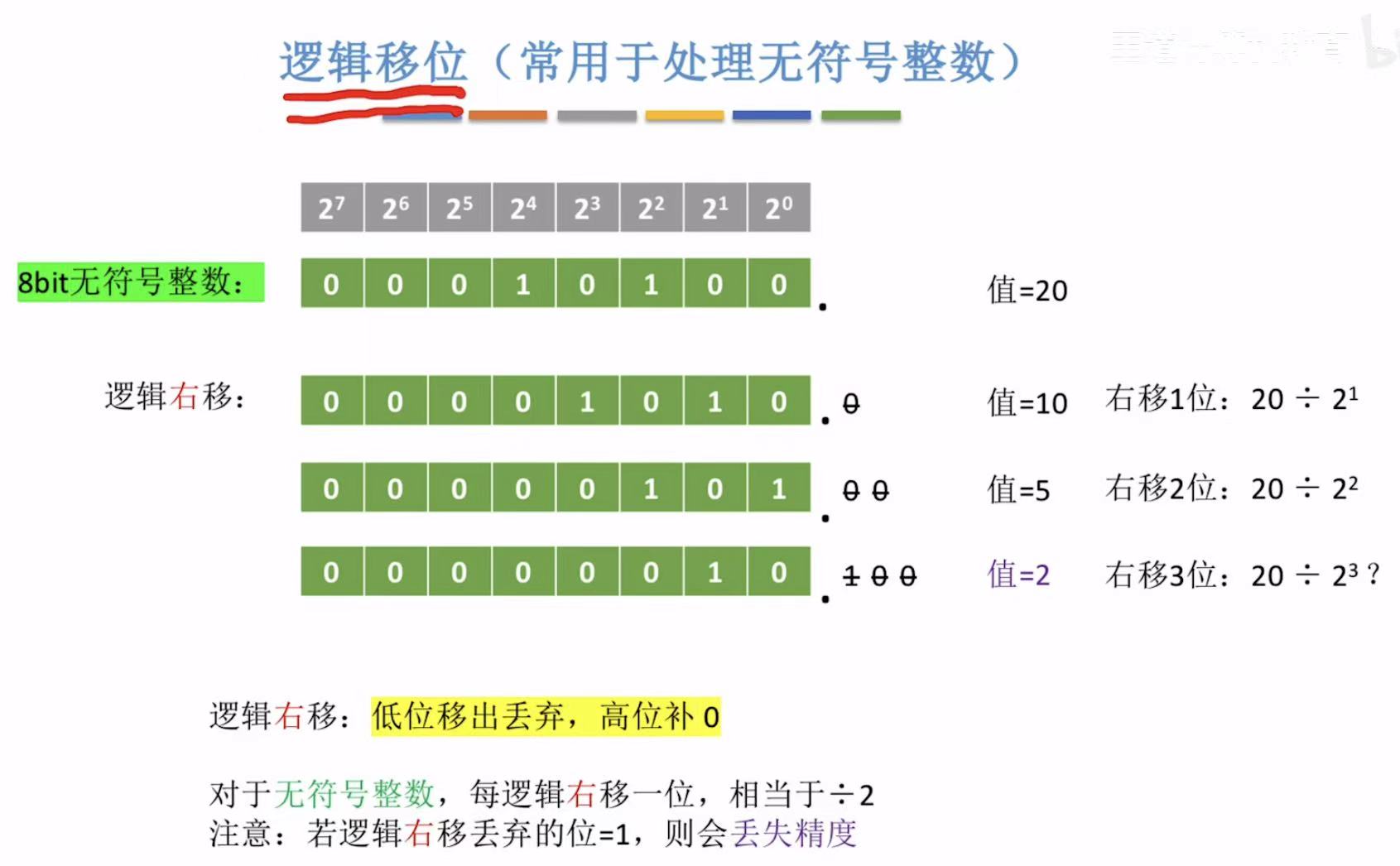
右移：移出0-->无影响，移出1-->丢失精度；
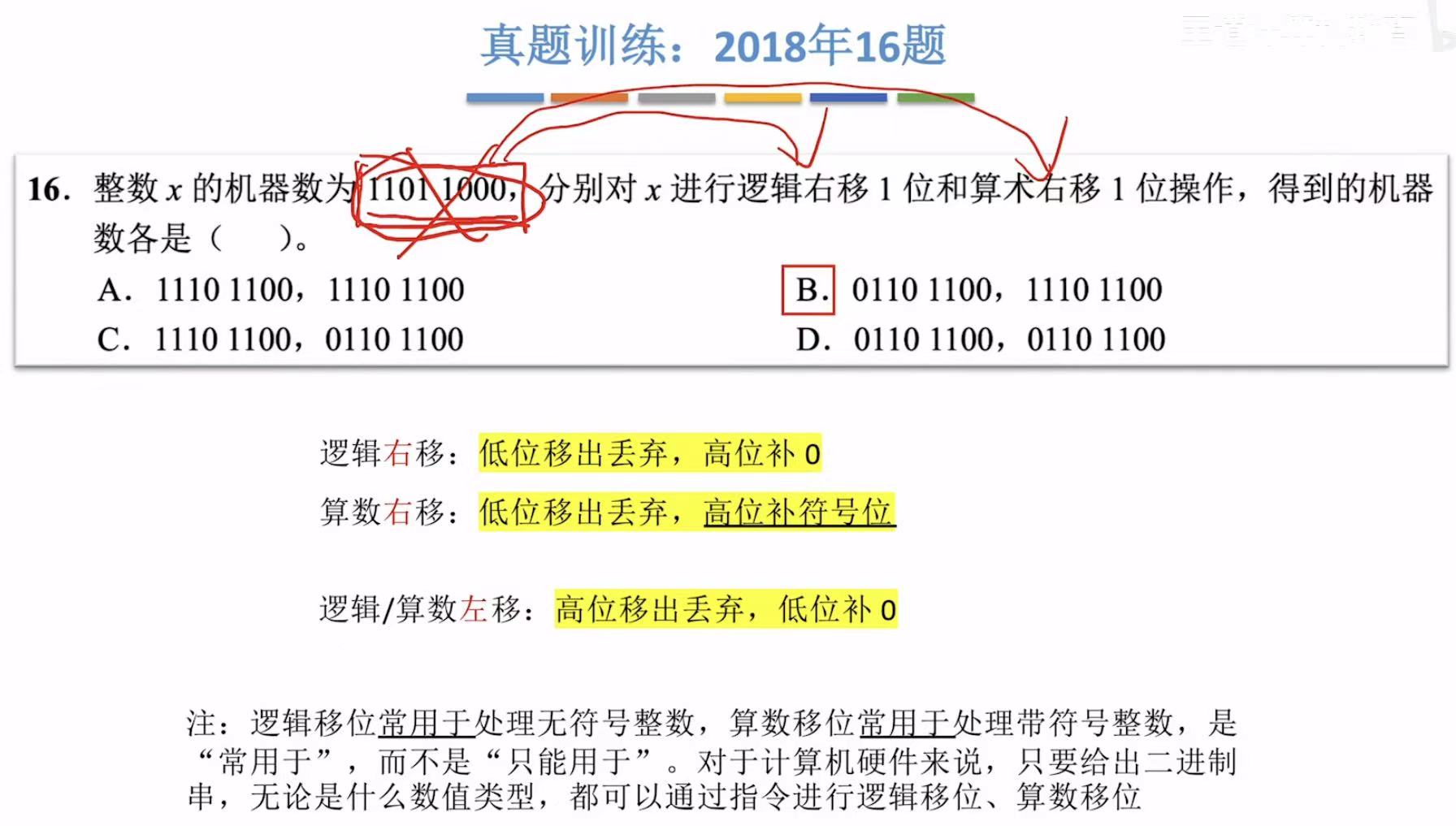
2. 算数移位（带符号）
带符号的溢出是由算数左移前后的符号位不同 来体现出的。
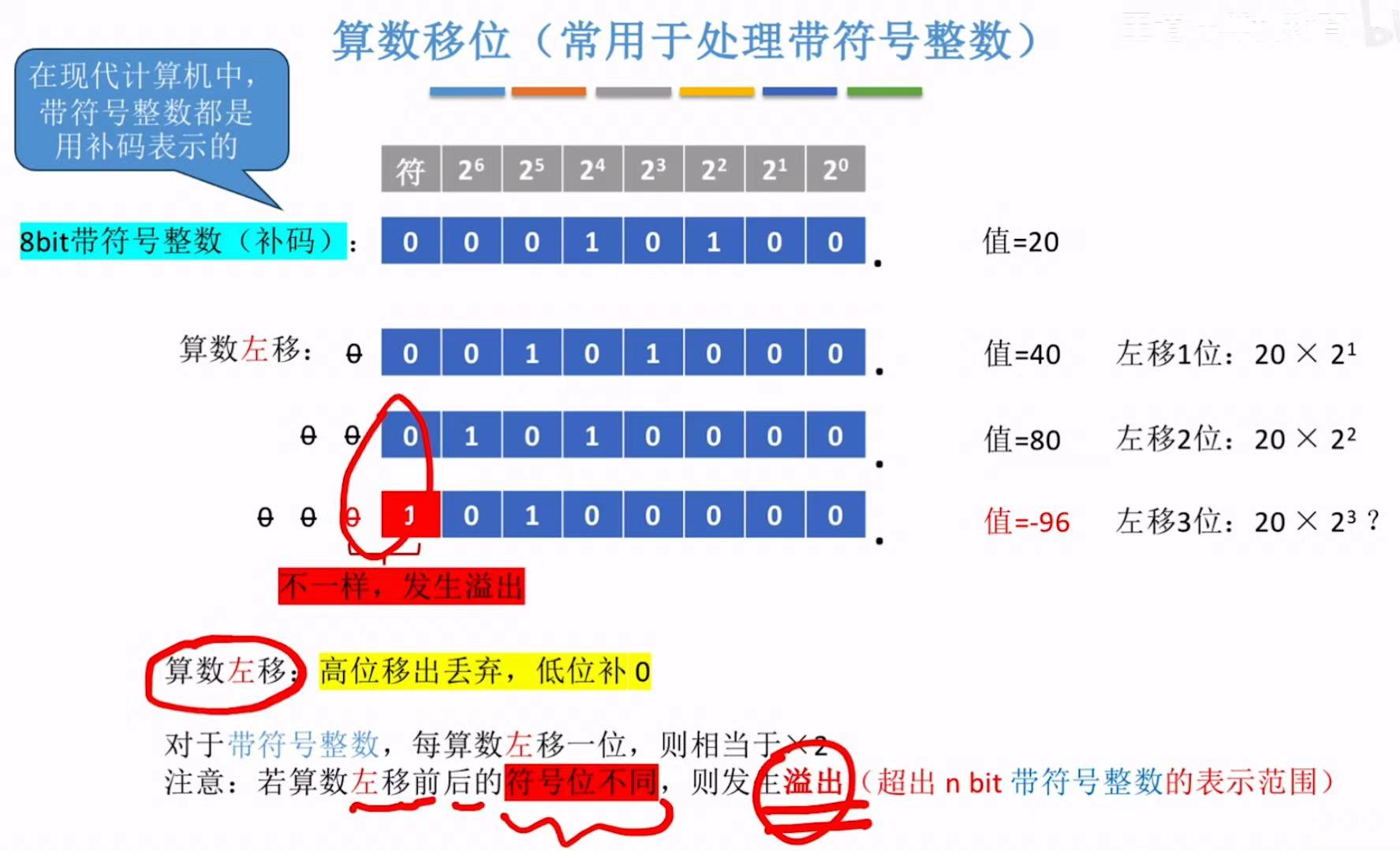
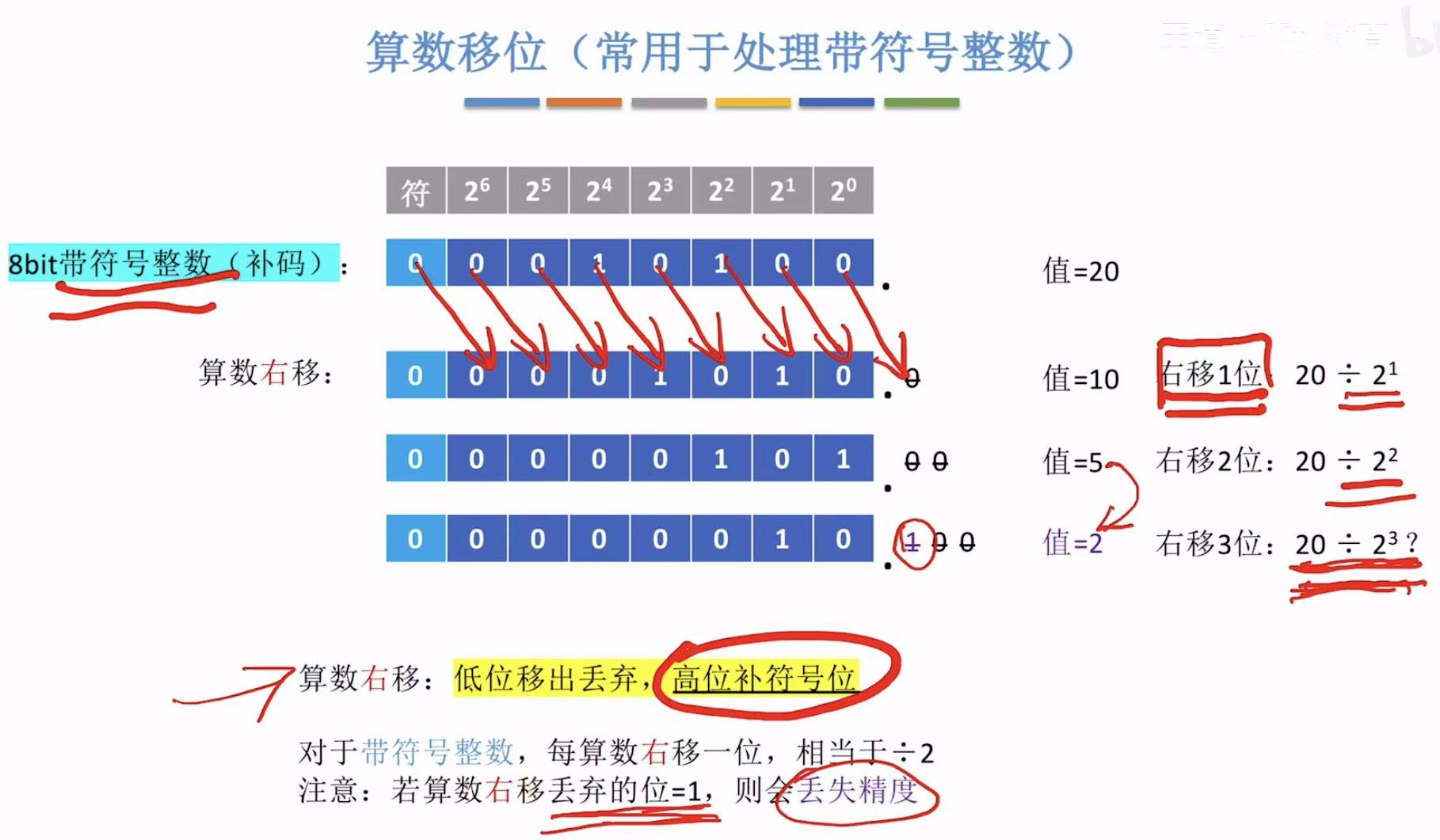
左移：移出0-->无影响，符号不同-->溢出；
右移：移出0-->无影响，移出1-->丢失精度；
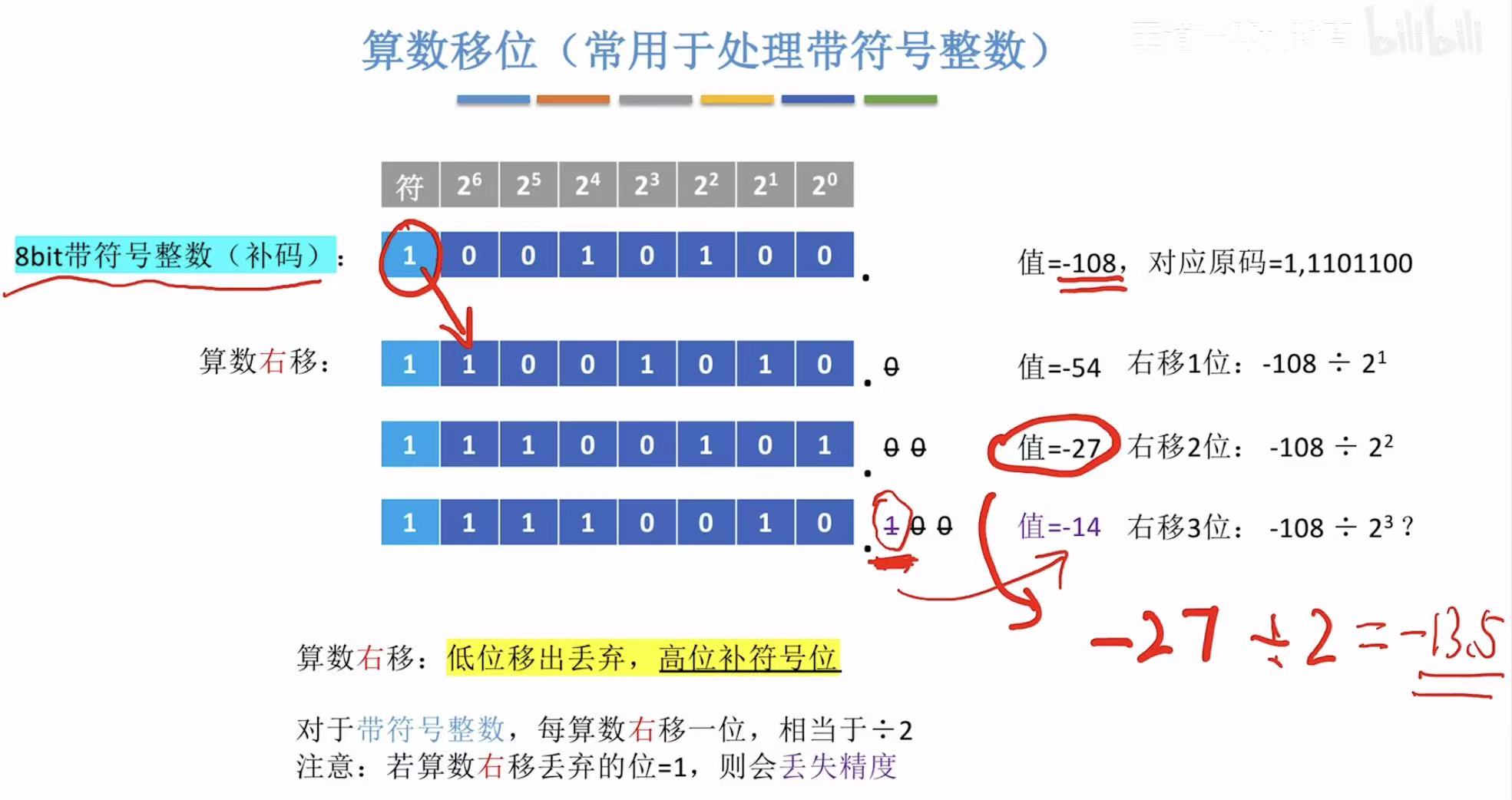
真题训练：
3. 小结
定点数的加减运算
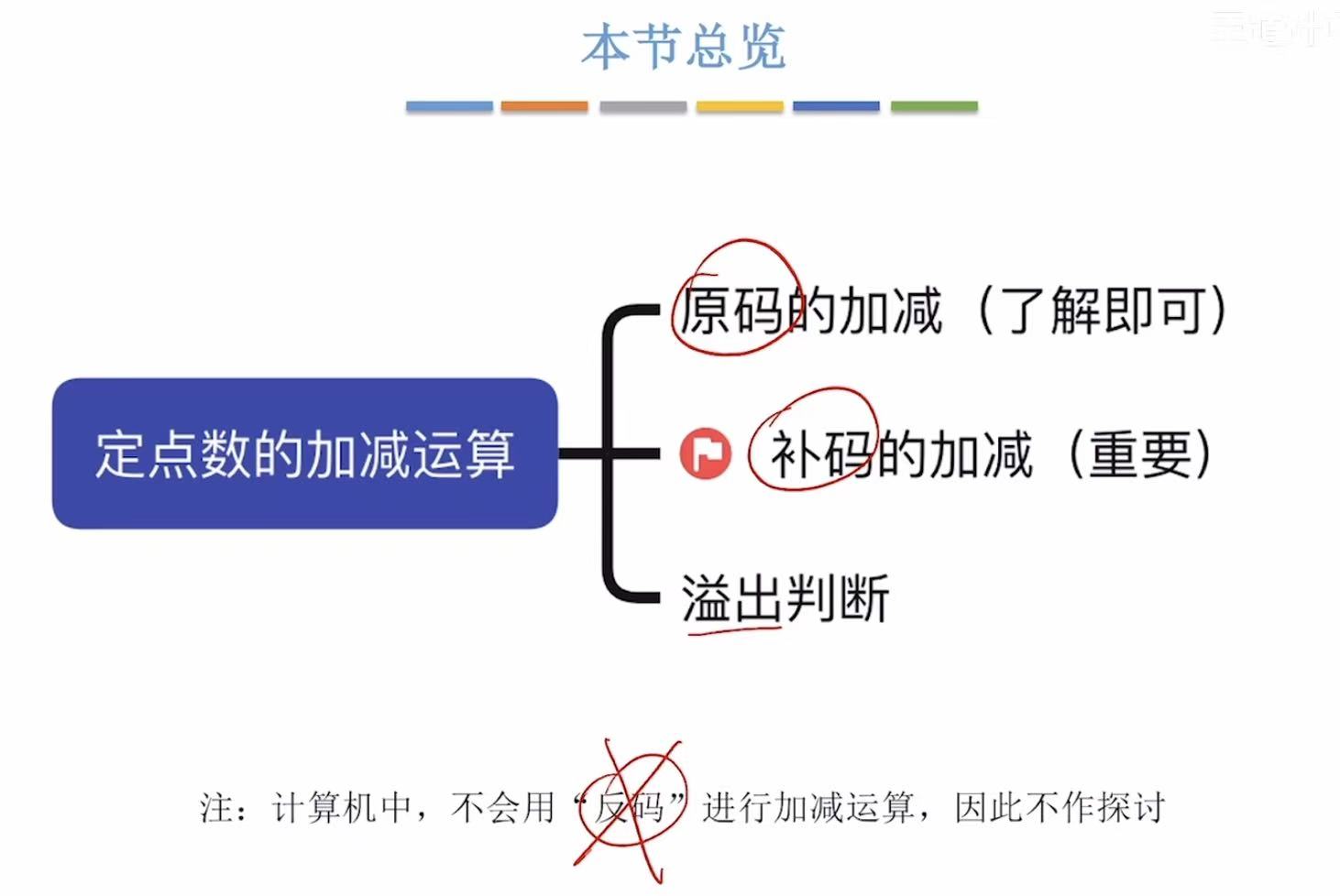
1. 原码的加减运算（不考）
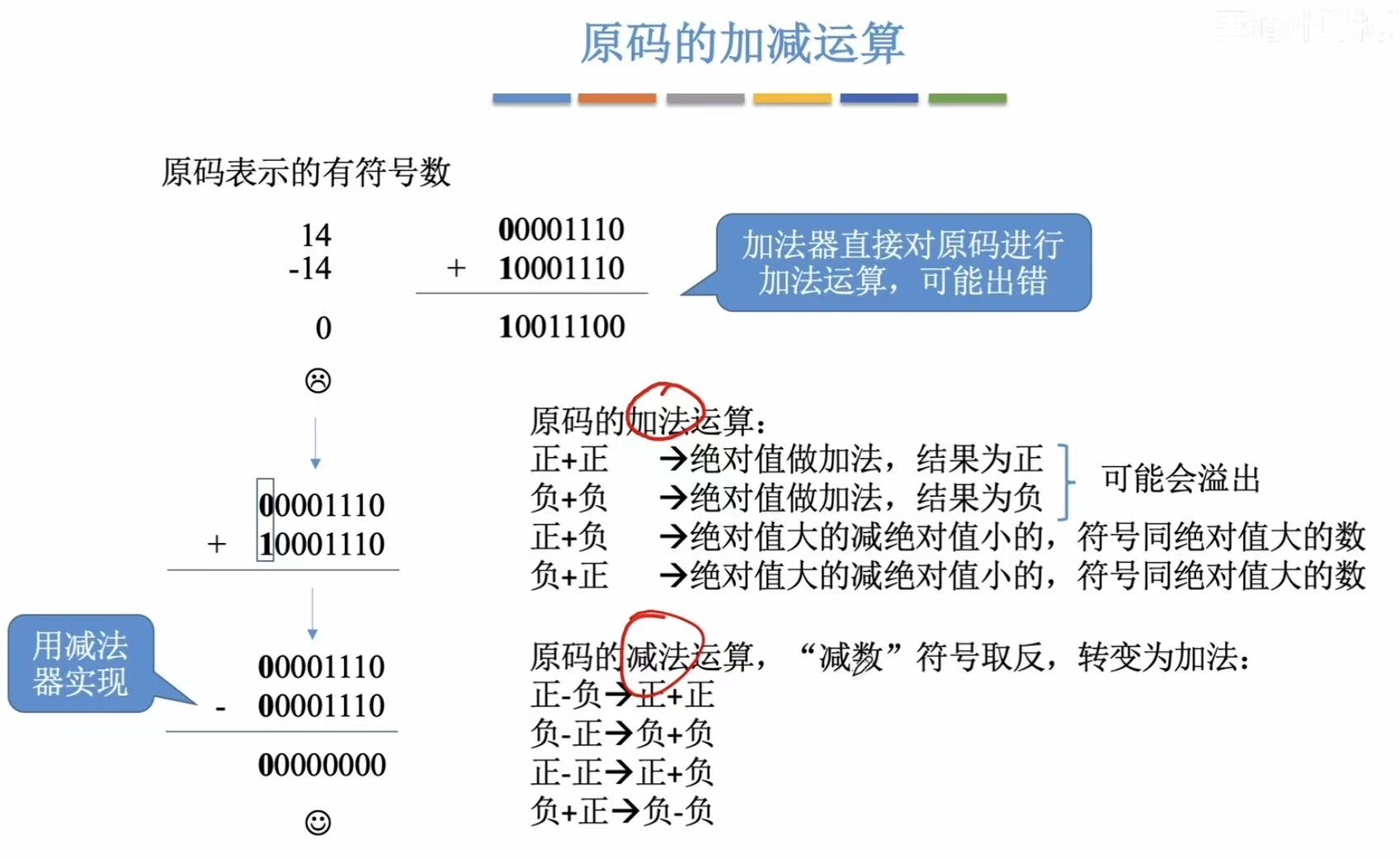
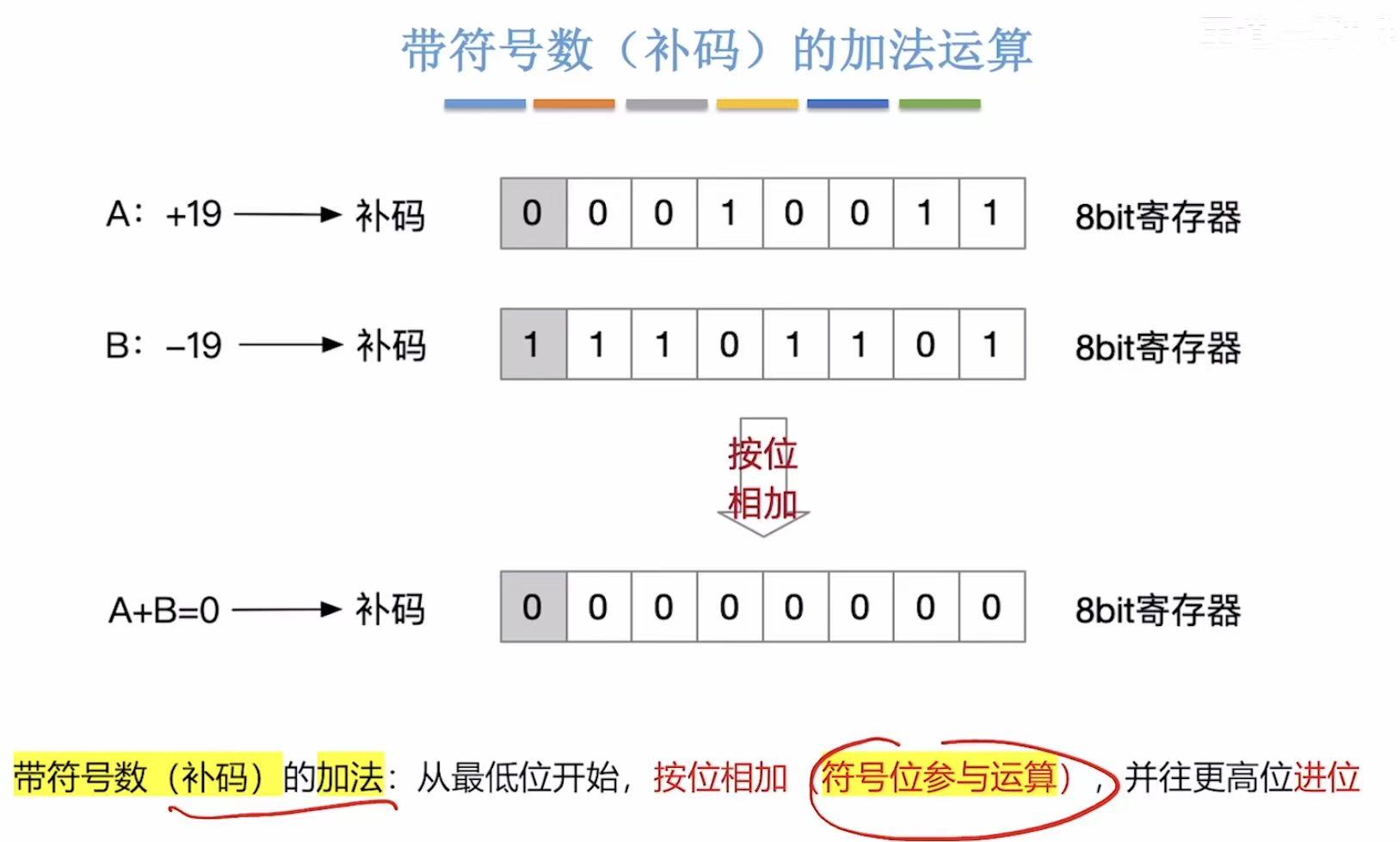
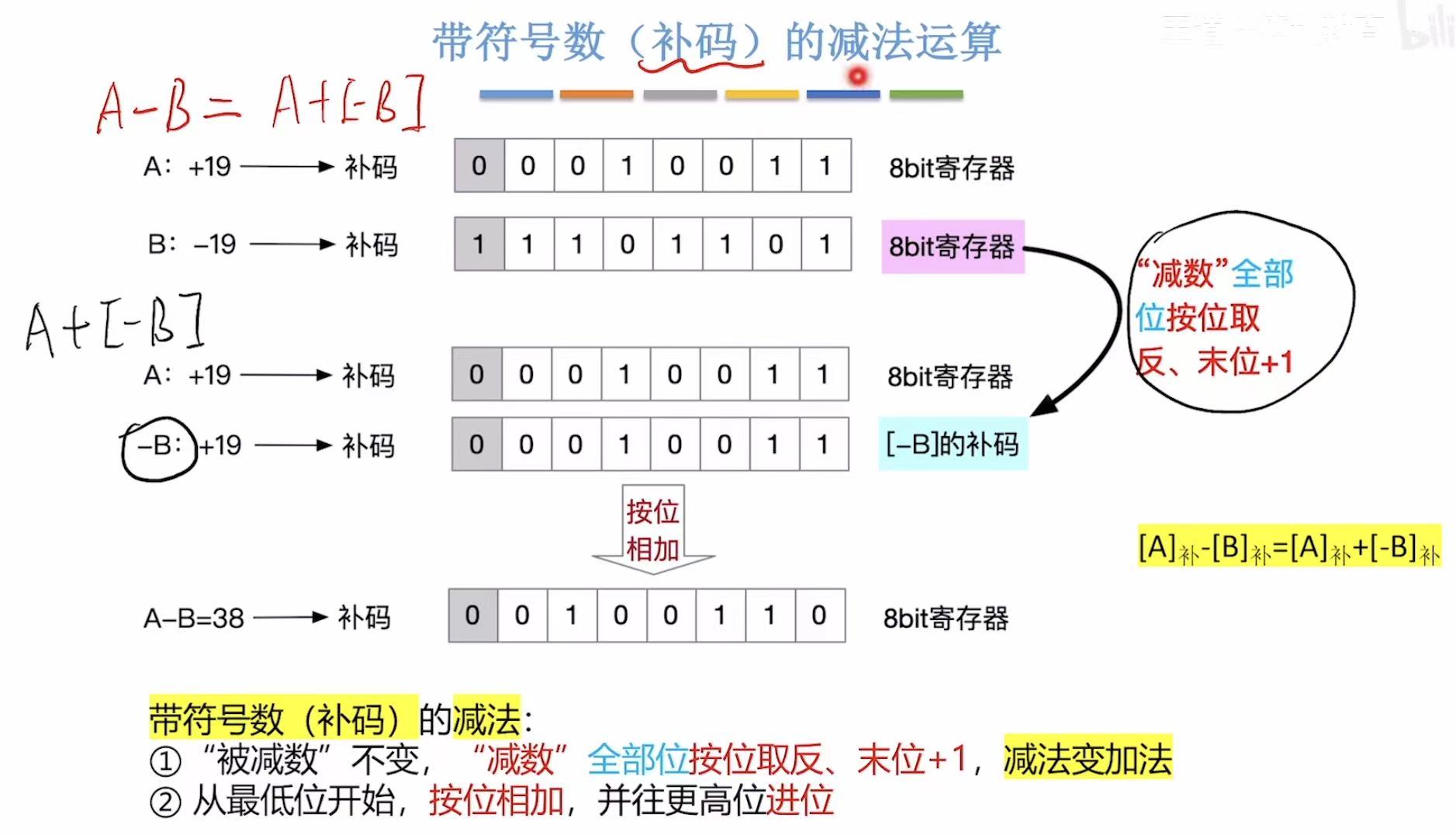
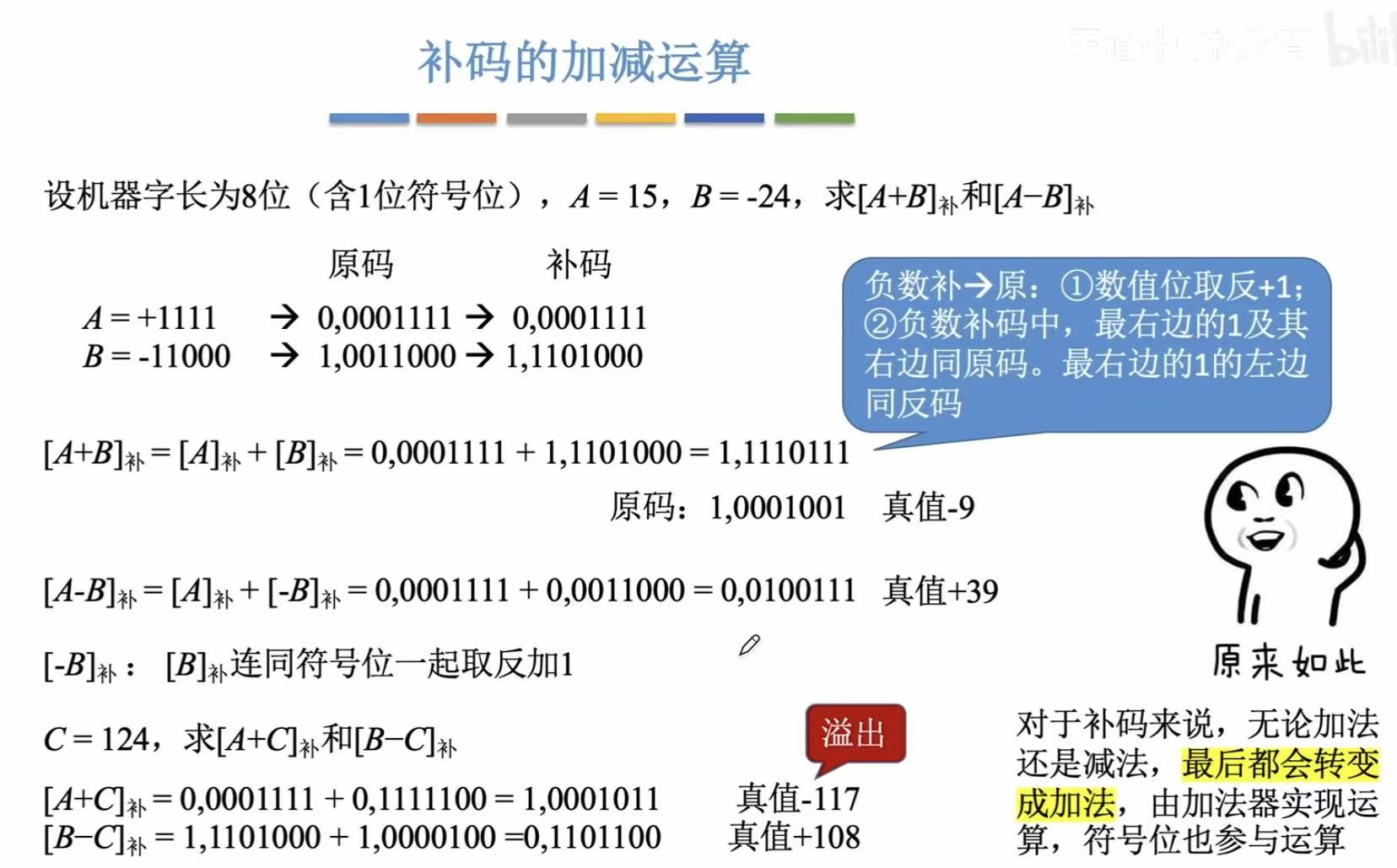
2. 补码的加减运算
负数的补码转为原码 有一个小技巧：符号位 和最后一个1 不变，中间的数全部取反即可。
1，1110111-->1，111011，1-->1，000100，1-->1，0001001
3. 溢出判断
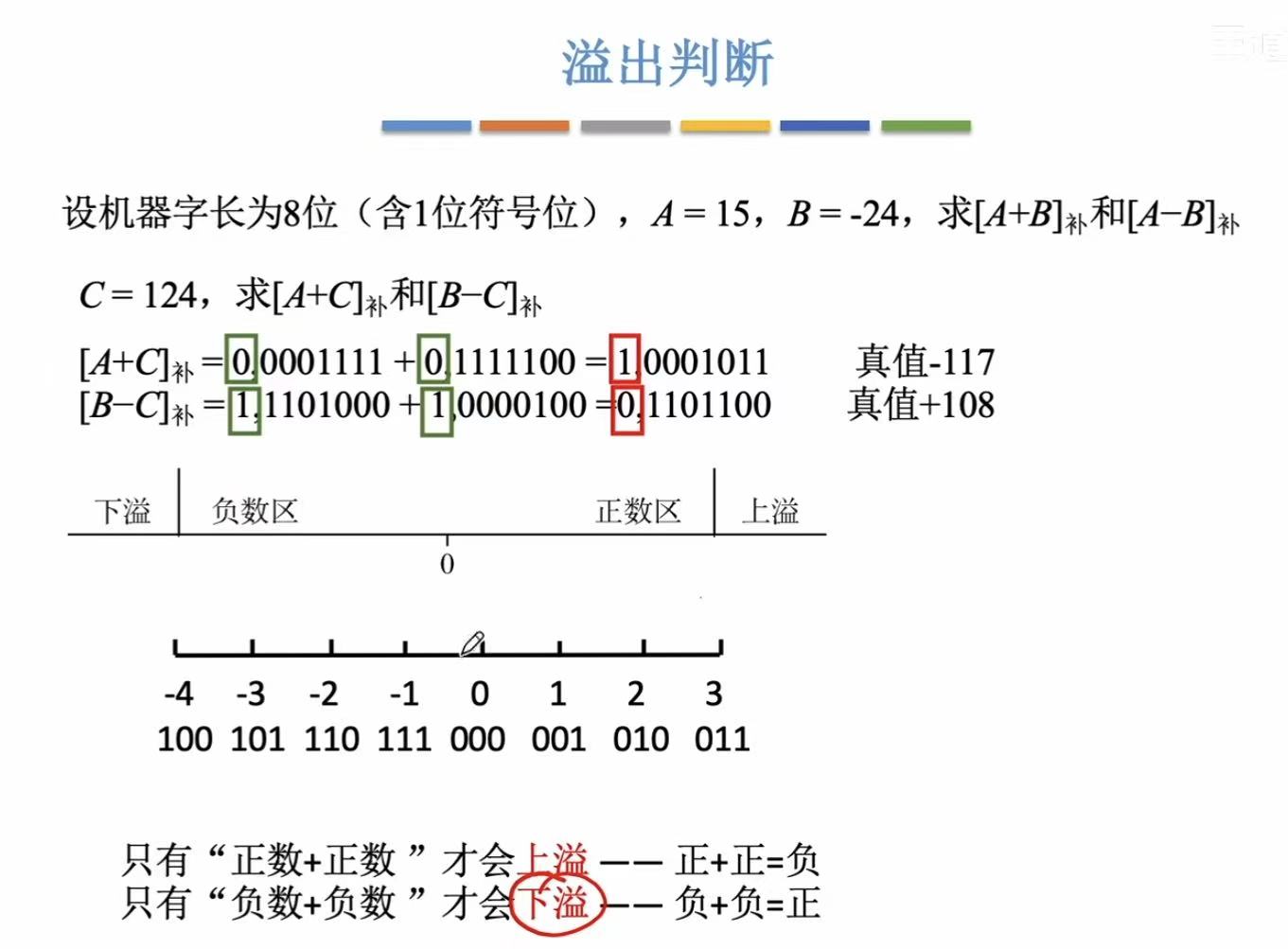
蓝色部分和上面图片表示的原理相同：负负得正，正正得负都是溢出。
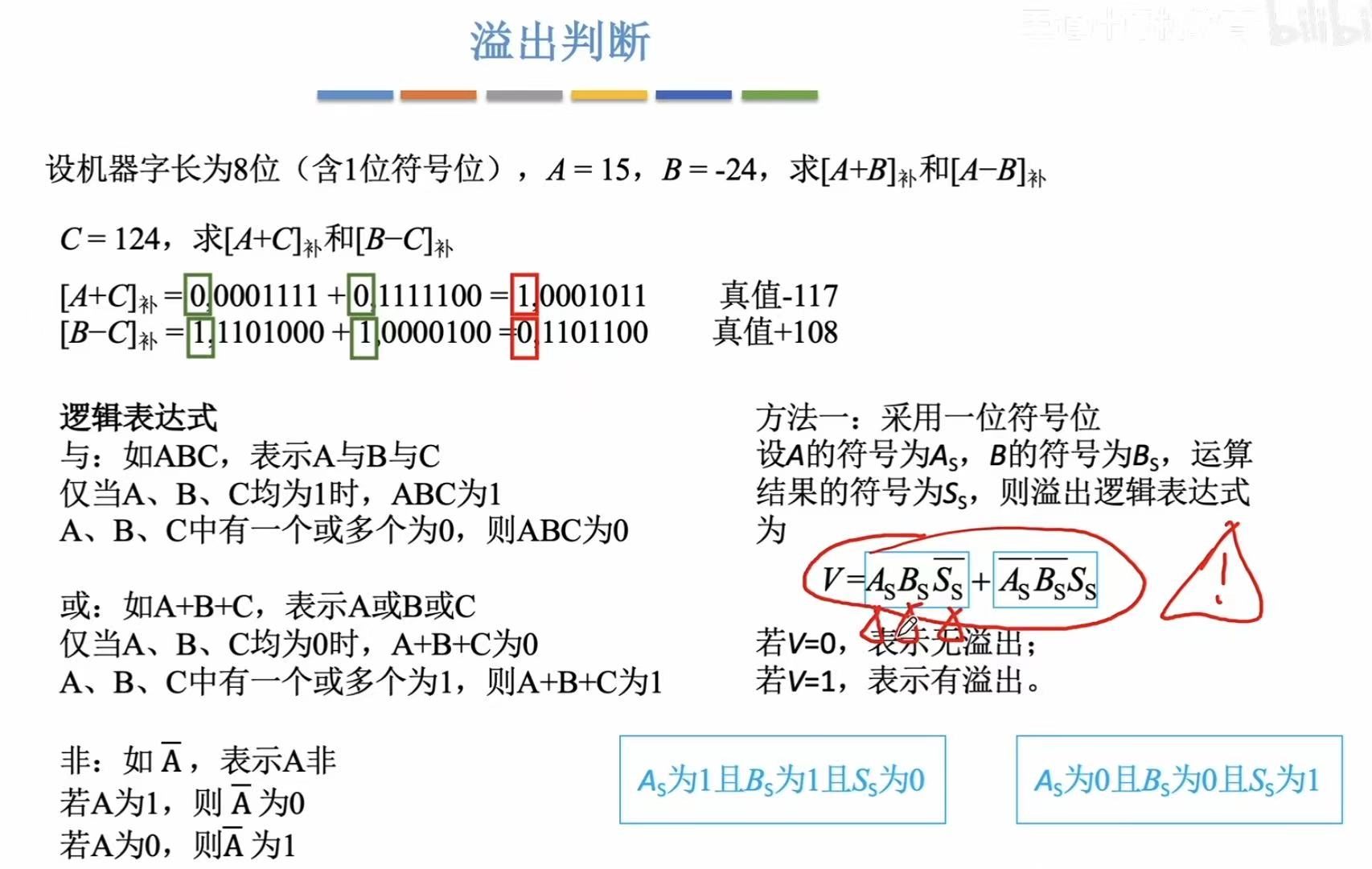
负负得正，正正得负，符合异或原理。
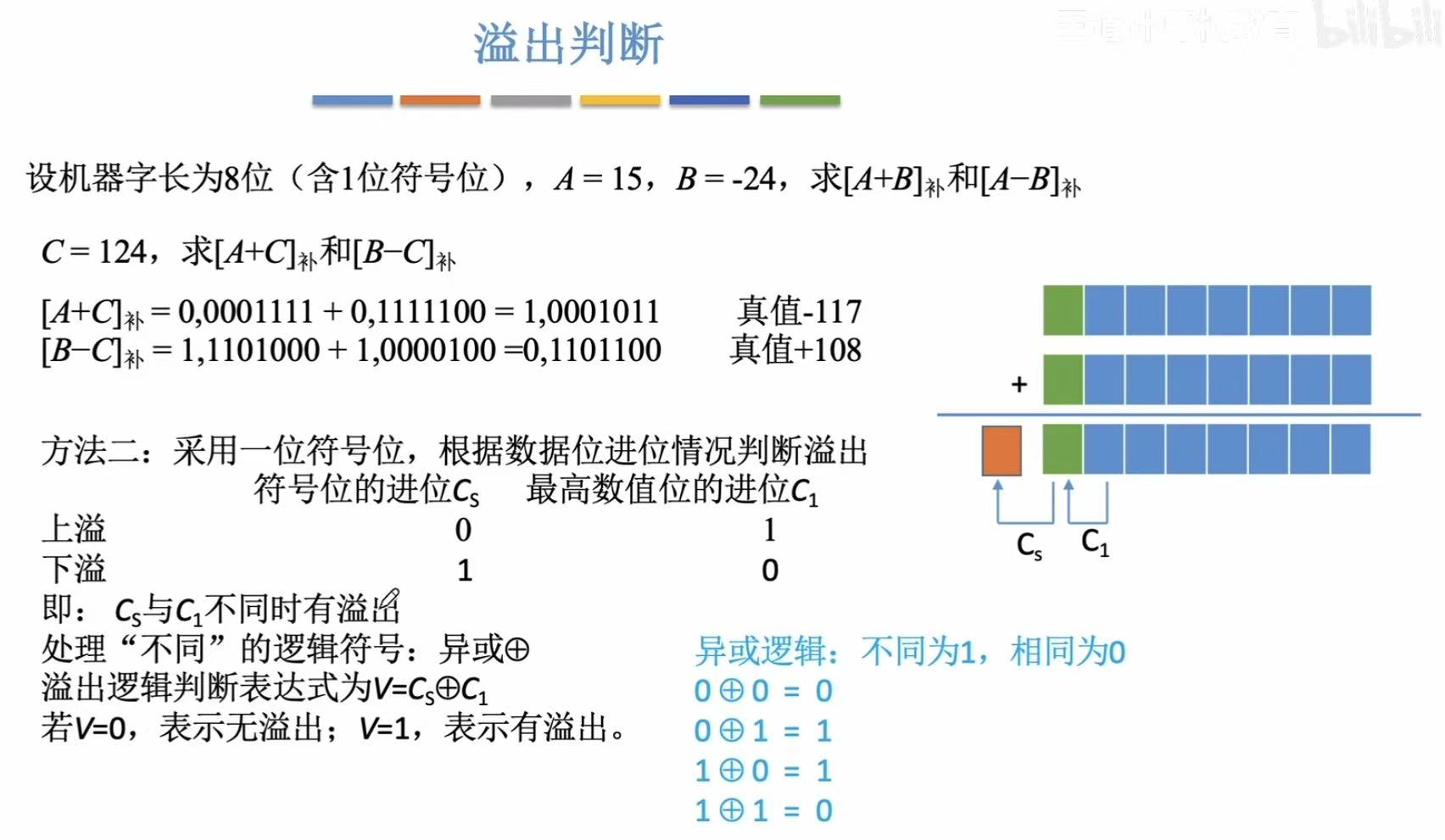
模2 ：1=20，前一位是21=2，模2就是保留2之后的数字 ，单符号位就是逗号之前只有一位20，也就是表示符号的一位，刚好是21后的一位，也就是刚好保留了2之后的数字，所以叫模2。
模4同理：11-->2120,它俩的前一位还有个22=4，保留的刚好是4之后的数字，所以叫模4。
4. 小结
无符号数的加减运算
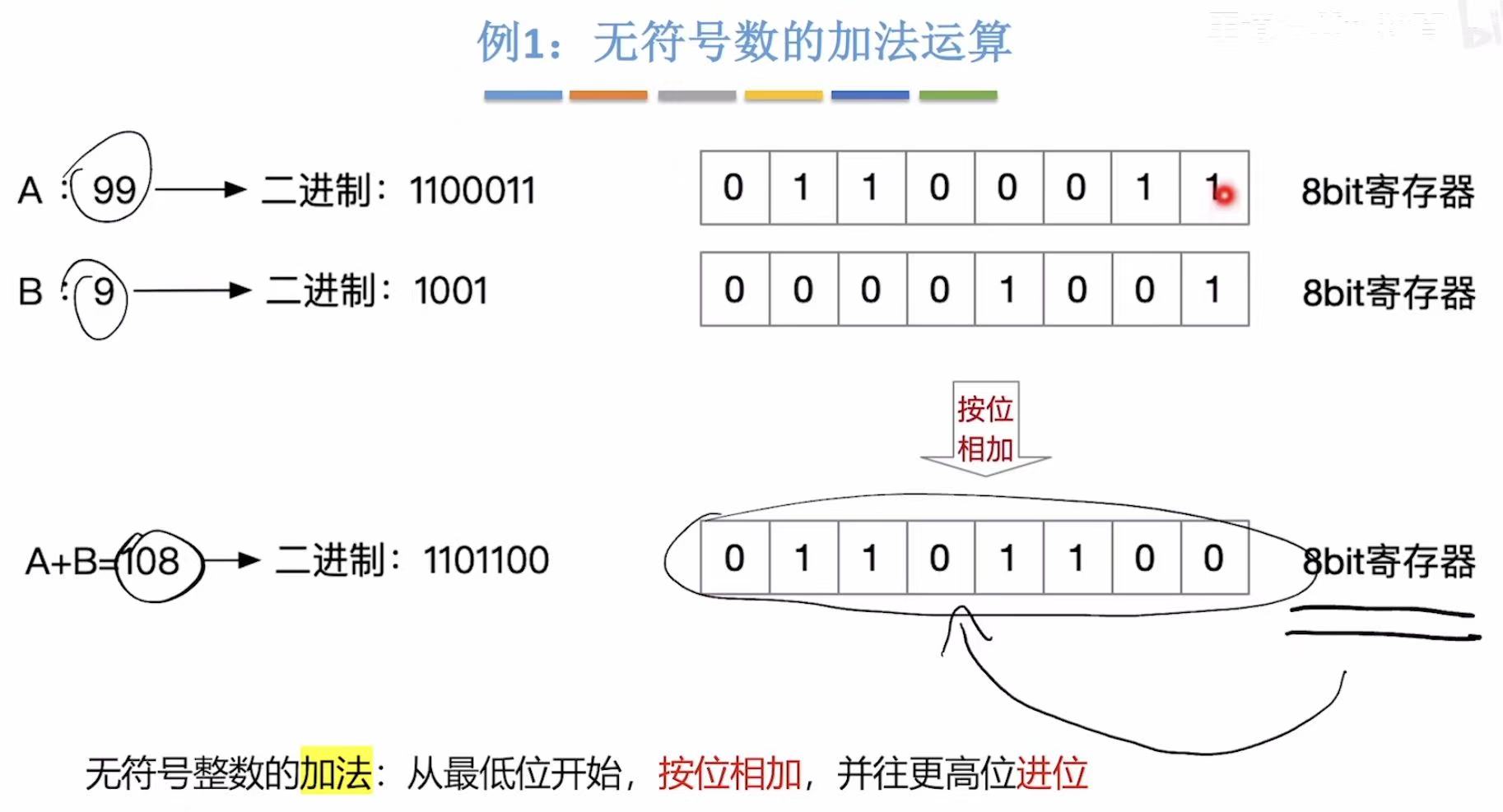
1. 无符号数的加法运算
回顾：
其实和带符号的一样。
2. 无符号数的减法运算
回顾：
这个和带符号的也一样。
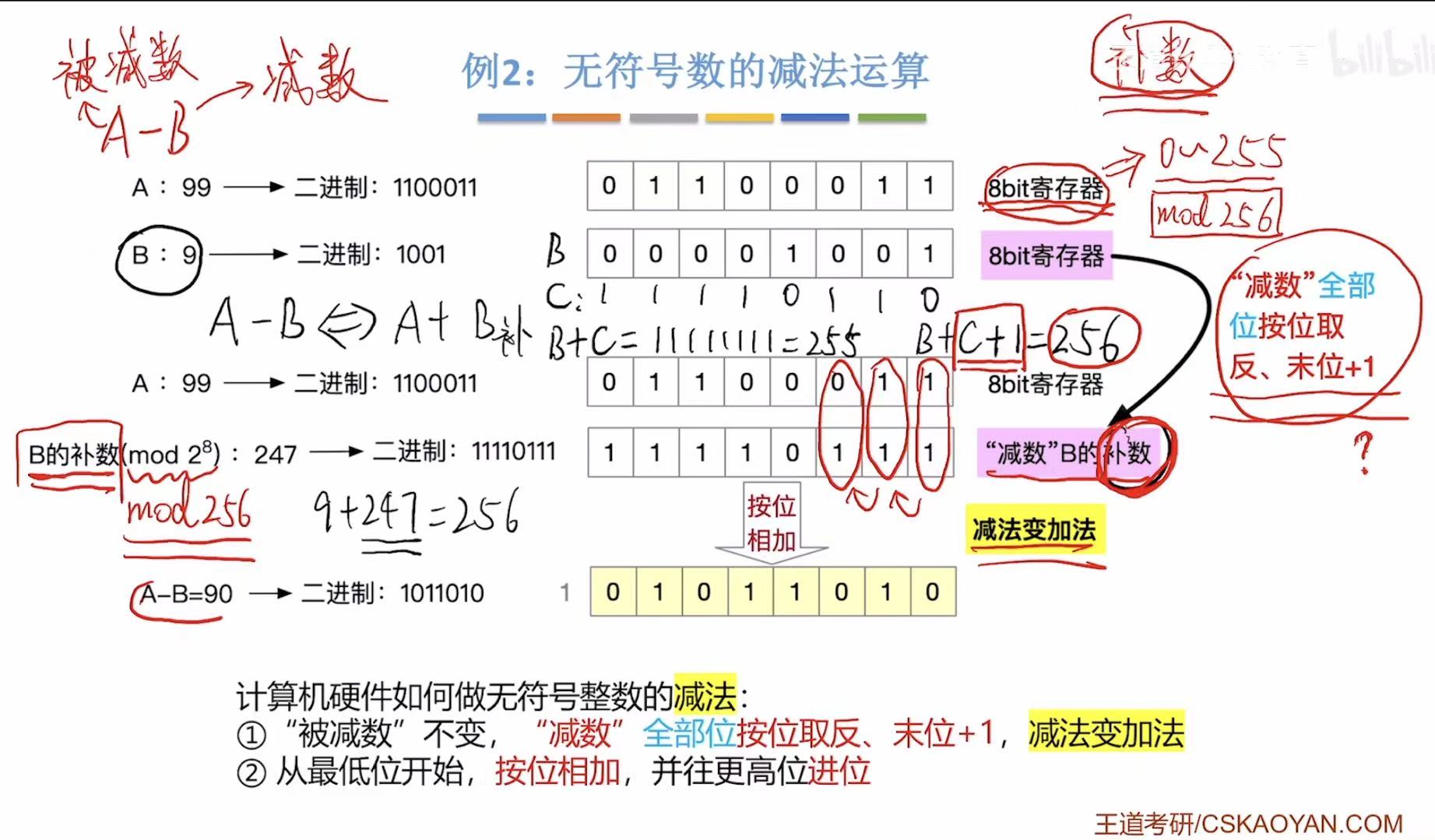
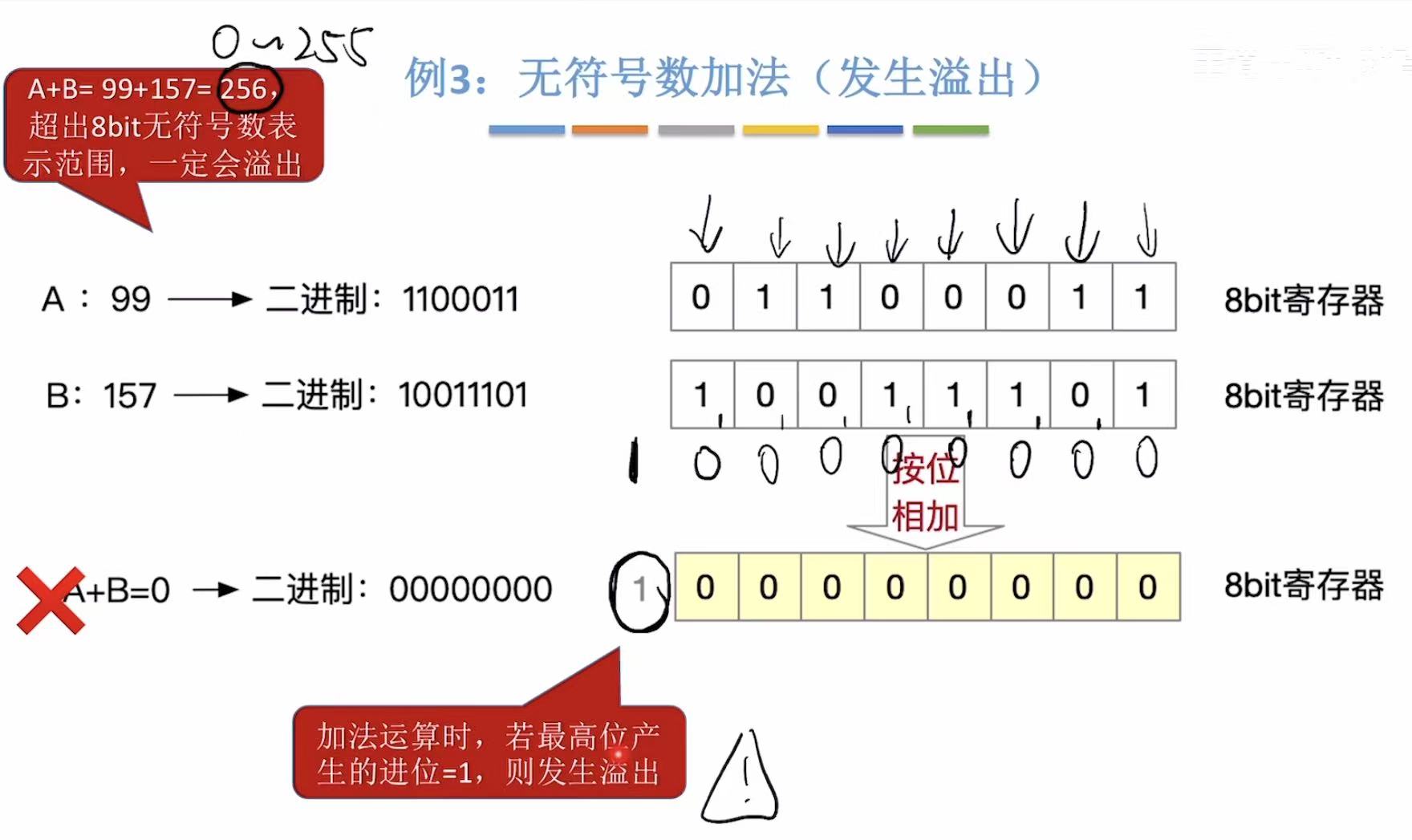
3. 溢出判断
纯手算，看结果在不在范围之内。
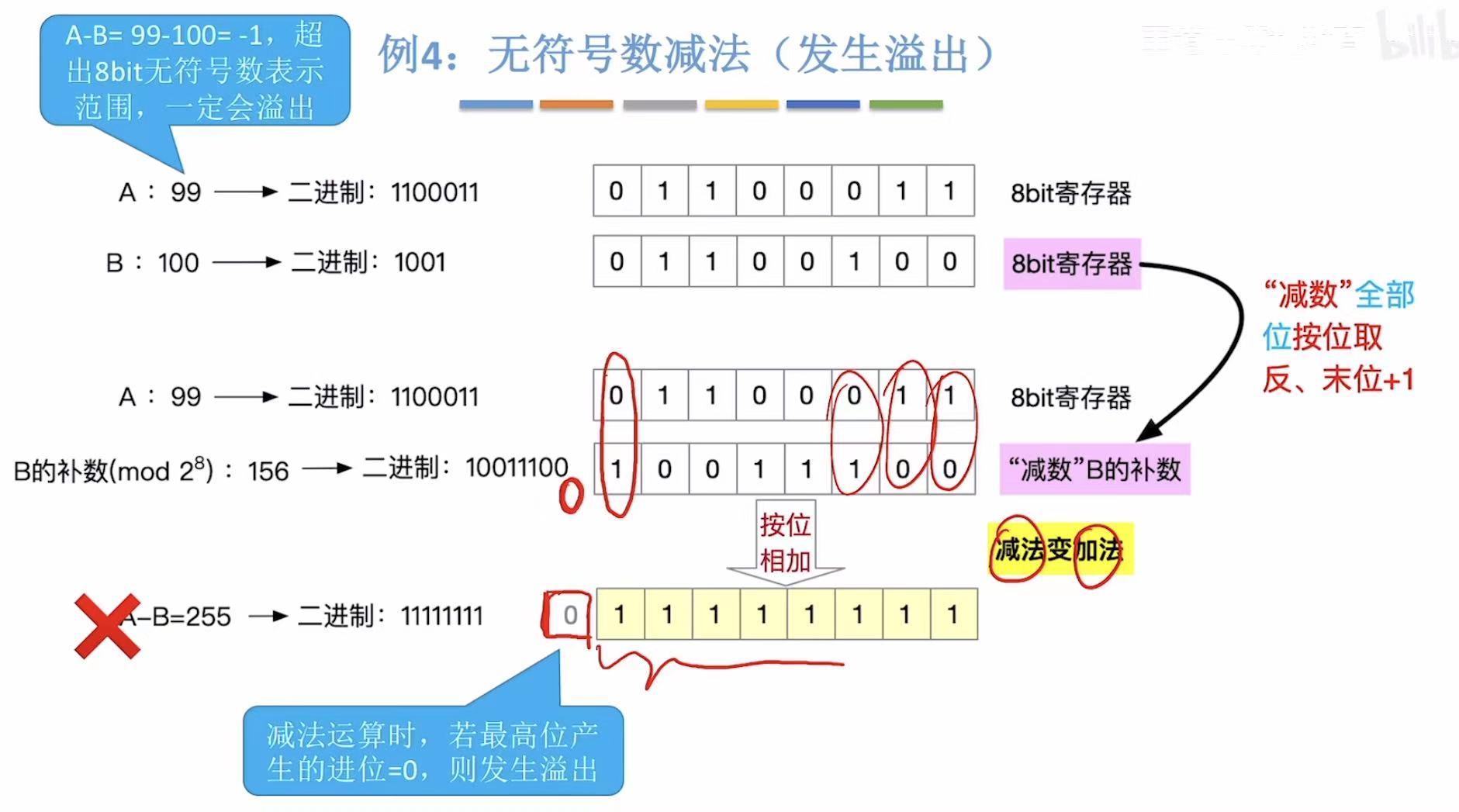
4. 小结
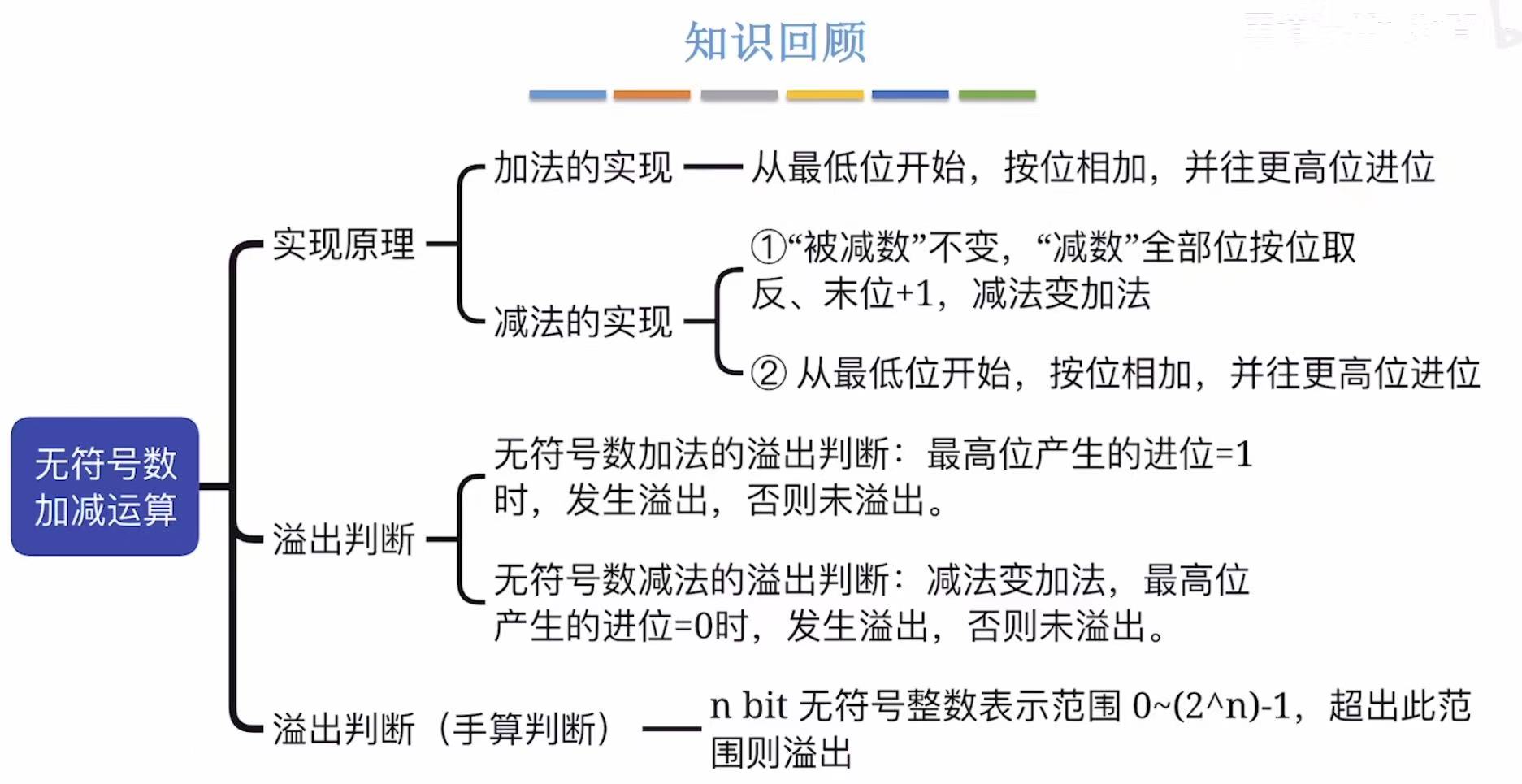
补码加减运算电路
回顾：
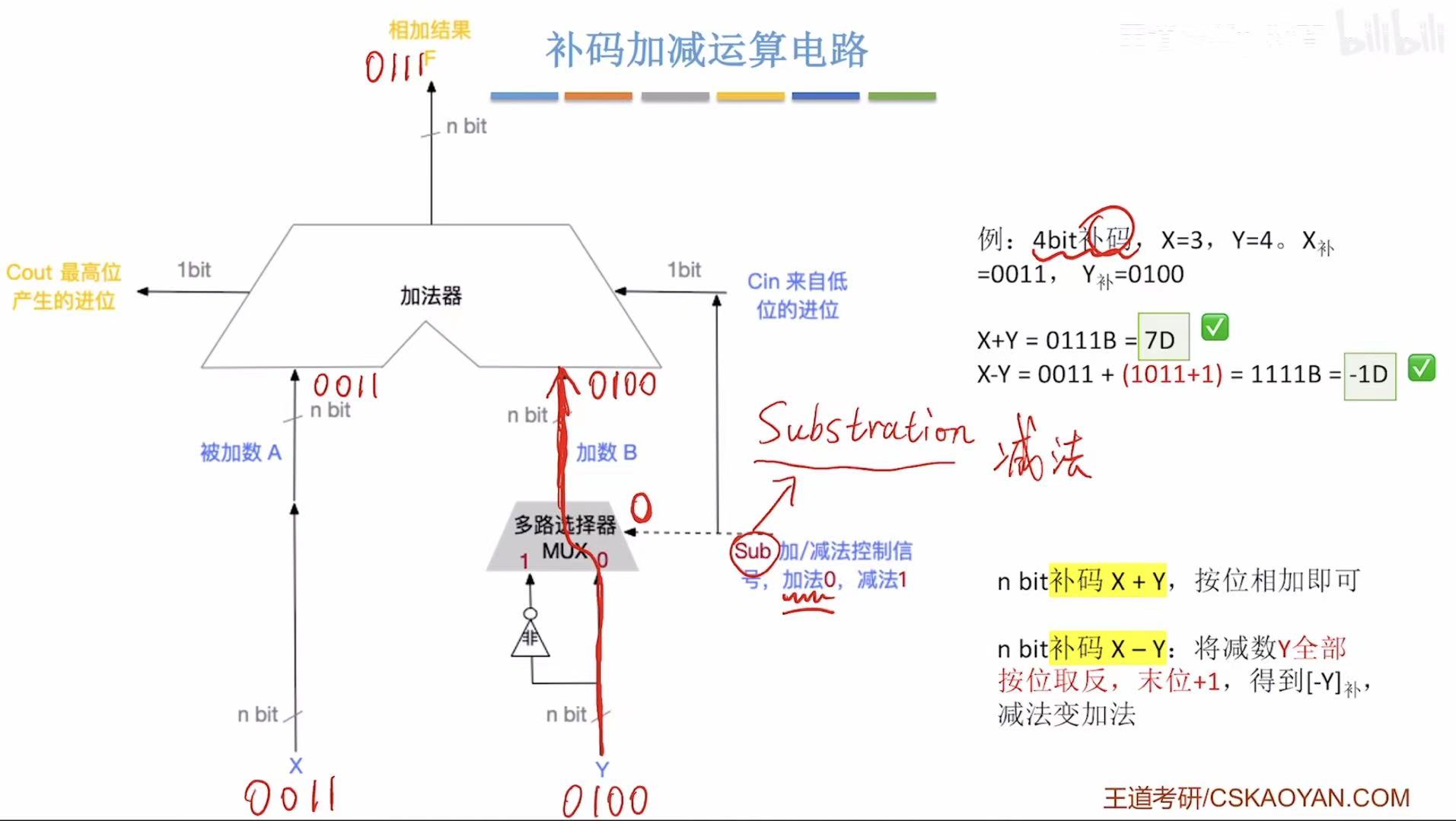
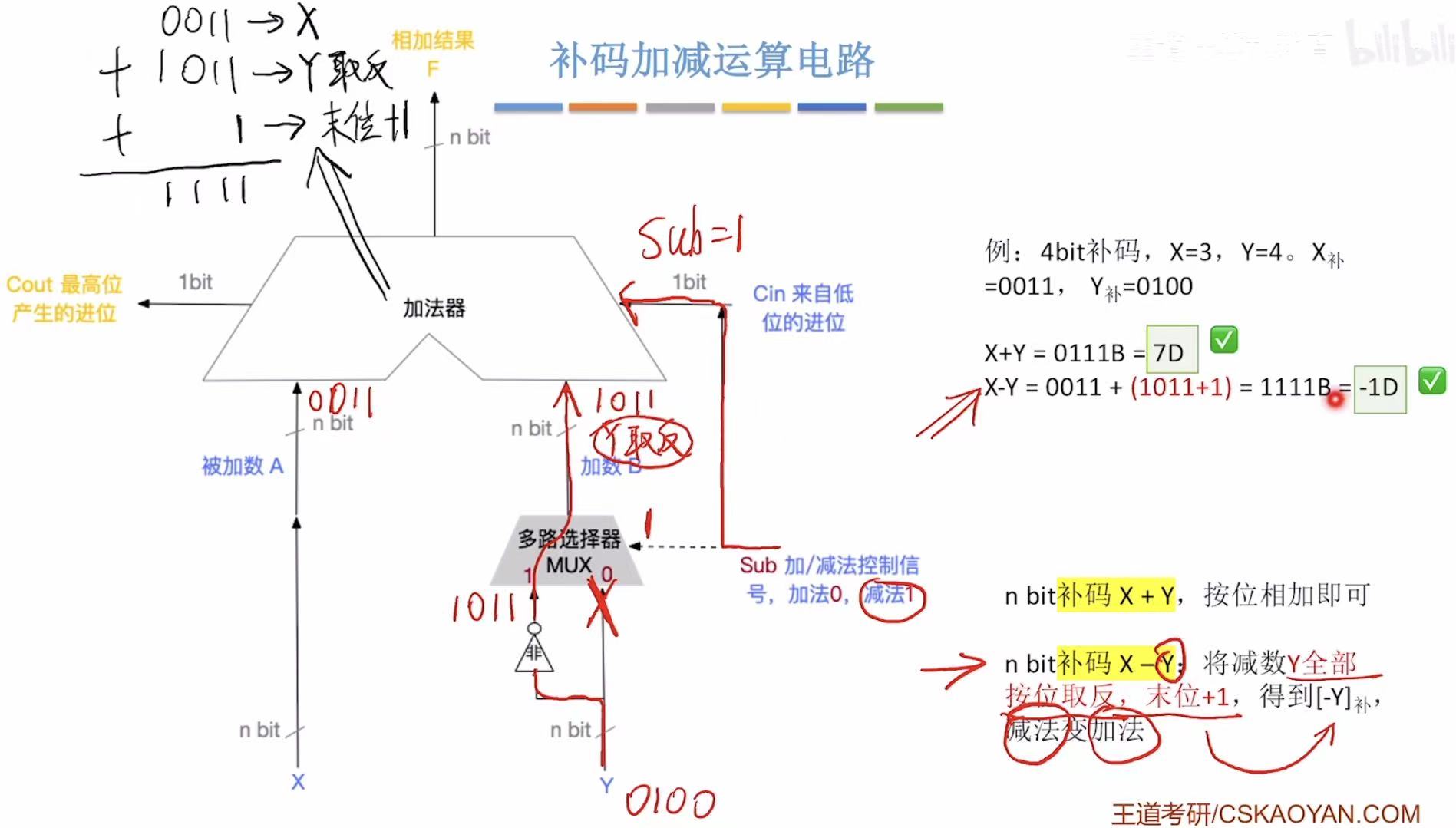
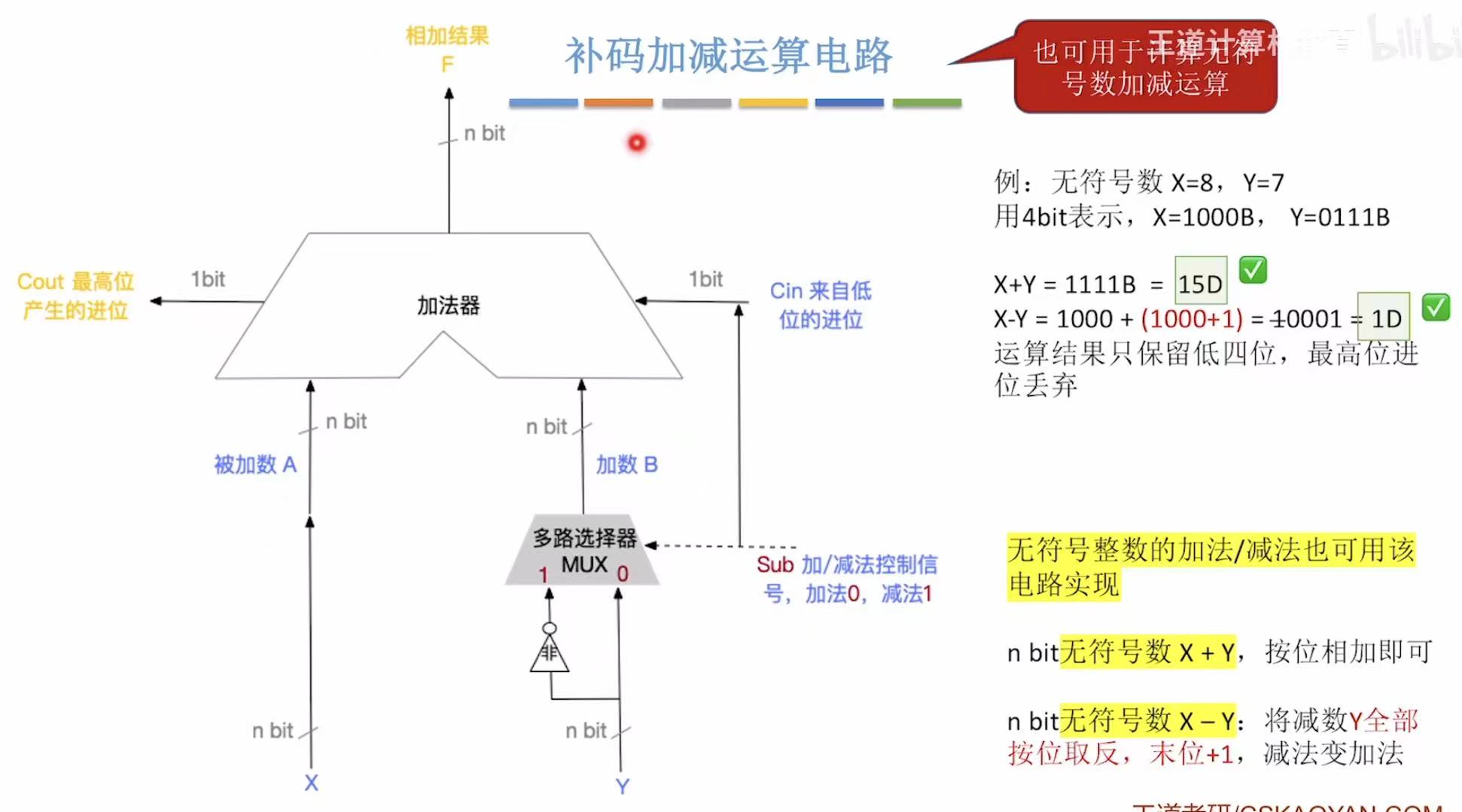
回顾：
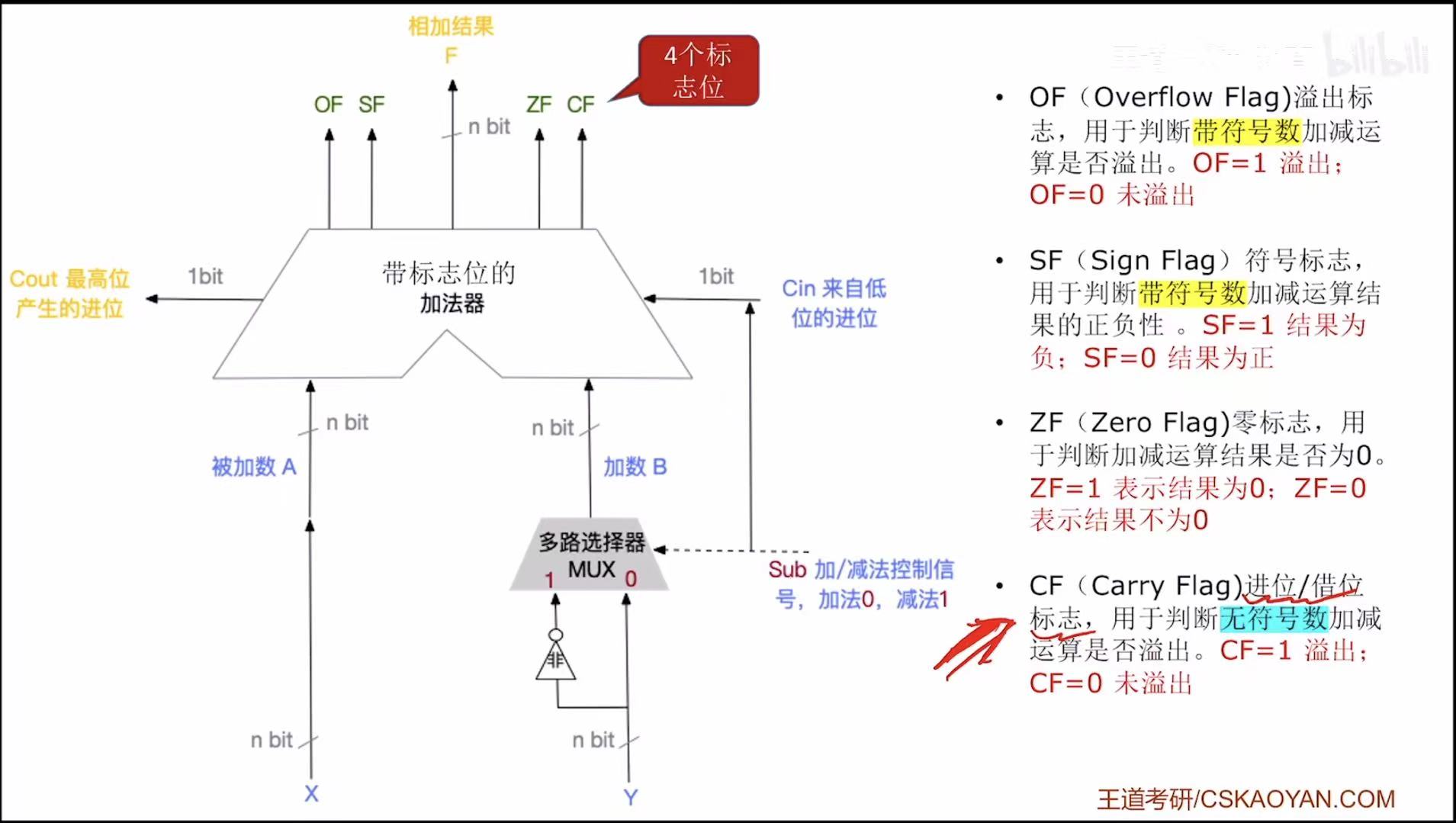
回顾：
