【数据结构】排序算法精讲 | 交换排序全解：交换思想、效率对比与实战代码剖析

蒙奇D索大2025-12-29 8:22

交换排序

  • 导读
  • 一、基本概念
    • [1.1 定义](#1.1 定义)
    • [1.2 算法分类](#1.2 算法分类)
  • [二、冒泡排序（bubble sort）](#二、冒泡排序（bubble sort）)
    • [2.1 定义](#2.1 定义)
    • [2.2 基本思想](#2.2 基本思想)
    • [2.3 排序过程](#2.3 排序过程)
      • [2.3.1 冒泡方式](#2.3.1 冒泡方式)
      • [2.3.2 第一轮冒泡](#2.3.2 第一轮冒泡)
      • [2.3.3 第二轮冒泡](#2.3.3 第二轮冒泡)
      • [2.3.4 第三轮冒泡](#2.3.4 第三轮冒泡)
      • [2.3.5 第四轮冒泡](#2.3.5 第四轮冒泡)
    • [2.4 C语言实现](#2.4 C语言实现)
      • [2.4.1 准备工作](#2.4.1 准备工作)
      • [2.4.2 函数三要素](#2.4.2 函数三要素)
      • [2.4.3 冒泡次数](#2.4.3 冒泡次数)
      • [2.4.4 一次冒泡的比较次数](#2.4.4 一次冒泡的比较次数)
      • [2.4.5 交换操作](#2.4.5 交换操作)
      • [2.4.6 性能分析](#2.4.6 性能分析)
      • [2.4.7 算法优化](#2.4.7 算法优化)
      • [2.4.8 算法代码](#2.4.8 算法代码)
  • 结语

导读

大家好，很高兴又和大家见面啦！！！

在前面的内容中，我们介绍了第一种内部排序------插入排序 ；

在 插入排序 中，按照具体的实现可以分为三类排序算法：

  • 直接插入排序 ：根据 插入排序 的思想直接实现的排序算法
  • 折半插入排序 ：将 折半查找 与 插入排序 相结合的排序算法，当数据量规模较大时，其算法效率要优于 直接插入排序
  • 希尔排序 ：通过引入 增量 d d d 将整体的 直接插入排序 拆分为了若干个 小规模的子序列 内部的 直接插入排序 ，充分利用了 直接插入排序 的优势。当数据规模 N N N 处于特定范围内时，算法效率能够达到 O ( N 1.3 ) O(N^{1.3}) O(N1.3)

插入排序思想 是一种 直观、稳定、低内存开销且在特定场景下高效的核心思想 。其通过 查找操作 、移动操作 以及 插入操作 的组合排序算法，能够通过创新（如希尔排序 ）或与其他思想融合（如混合排序 ）来不断适应更复杂的需求。

接下来我们将会开始进入内部排序的第二种算法------ 交换排序 。

我们会通过 交换排序 算法来逐步体会 交换思想 的独特魅力与智慧。下面就让我直接进入今天的内容；

一、基本概念

1.1 定义

交换 ：根据序列中两个元素关键字的比较结果来对换着两个记录在序列中的位置。

简单的理解就是，当我们要将 [ 2 , 1 ] [2, 1] [2,1] 以升序排列时，我们需要做的就是两步：

  • 比较 ： 2 > 1 2 > 1 2>1 ，不满足升序要求
  • 交换 ： 2 2 2 与 1 1 1 互换位置 [ 1 , 2 ] [1, 2] [1,2]

交换排序 实际上就是以 交换思想 为核心完成 排序。

1.2 算法分类

交换排序 并不是单指某一个算法，它同样也是一种 算法思想 。

与 插入排序思想 不同，交换排序思想 可以总结为两步：

  • 比较：将两个元素进行对比，判断二者之间的关系
  • 交换 ：将不满足要求的双方进行 位置互换

基于该算法思想的排序算法有很多，下面我们就简单介绍几种：

  • 冒泡排序 ：交换排序思想 的最直接的体现
  • 快速排序 ：交换排序 与 分治策略 的相结合的 高效排序
  • 鸡尾酒排序 ：冒泡排序 的变种------双向冒泡排序
  • 地精排序 ：交换排序思想 与 插入排序思路 相结合的 单循环排序
  • 奇偶排序 ：冒泡排序 的 并行化改进 ------奇偶索引对比较
  • 臭皮匠排序 ：交换排序 与 分治策略 相结合的 低效递归排序

在这些算法中，我们主要会学习------冒泡排序 以及 快速排序 。通过这两种算法，我们会初步感受到 交换思想 的独特魅力，下面就让我们进入今天的内容；

二、冒泡排序（bubble sort）

2.1 定义

冒泡排序 （Bubble Sort ）又称为 起泡排序 、气泡排序 或 泡沫排序 是一种直观的排序算法。它通过反复比较相邻元素并交换顺序错误的元素，使较大（或较小）的元素逐渐"浮"到序列的一端，从而实现排序。

2.2 基本思想

冒泡排序 的基本思想是：

  • 从后往前（或从前往后）两两比较相邻元素的值
  • 若相比较的元素为 逆序 （即要求升序，而元素排列为 降序 ，或要求 降序 ，而元素排列为 升序），则交换它们
  • 重复上述过程，直到所有元素完成 正序 排列

2.3 排序过程

为了更直观的感受整个 冒泡 的过程，我们以 关键字序列 [5, 4, 3, 2, 1] 为例，通过 冒泡排序 使其完成 升序排列；

2.3.1 冒泡方式

对于 N N N 个元素的 关键字序列 ，当我们通过 冒泡排序 使其完成 升序排列 时，不同的 冒泡方式 所完成的过程也会有所区别：

  • 从前往后冒泡 ：每一轮 冒泡 都会确定一个 最大值
  • 从后往前冒泡 ：每一轮 冒泡 都会确定一个 最小值

这里我们选择 从前往后冒泡 的方式来完成最终的排序任务；

2.3.2 第一轮冒泡

我们示例中的 关键字序列 长度为 L = 5 L = 5 L=5 ，因此 从前往后冒泡 实际上是指：从下标 0 开始往后排序 。

在第一轮 冒泡 中，我们需要完成 4 4 4 次 比较 ：

  • 第一次比较： 5 > 4 5 > 4 5>4 ，关键字 逆序 ，需要执行 交换
下标 0 1 2 3 4
交换前： 5 \bm{\textcolor{red}{5}} 5 4 \bm{\textcolor{blue}{4}} 4 3 \bm{\textcolor{black}{3}} 3 2 \bm{\textcolor{black}{2}} 2 1 \bm{\textcolor{black}{1}} 1
交换后： 4 \bm{\textcolor{blue}{4}} 4 5 \bm{\textcolor{red}{5}} 5 3 \bm{\textcolor{black}{3}} 3 2 \bm{\textcolor{black}{2}} 2 1 \bm{\textcolor{black}{1}} 1
  • 第二次比较： 5 > 3 5 > 3 5>3 ，关键字 逆序 ，需要执行 交换
下标 0 1 2 3 4
交换前： 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{red}{5}} 5 3 \bm{\textcolor{blue}{3}} 3 2 \bm{\textcolor{black}{2}} 2 1 \bm{\textcolor{black}{1}} 1
交换后： 4 \bm{\textcolor{black}{4}} 4 3 \bm{\textcolor{blue}{3}} 3 5 \bm{\textcolor{red}{5}} 5 2 \bm{\textcolor{black}{2}} 2 1 \bm{\textcolor{black}{1}} 1
  • 第三次比较： 5 > 2 5 > 2 5>2 ，关键字 逆序 ，需要执行 交换
下标 0 1 2 3 4
交换前： 4 \bm{\textcolor{black}{4}} 4 3 \bm{\textcolor{black}{3}} 3 5 \bm{\textcolor{red}{5}} 5 2 \bm{\textcolor{blue}{2}} 2 1 \bm{\textcolor{black}{1}} 1
交换后： 4 \bm{\textcolor{black}{4}} 4 3 \bm{\textcolor{black}{3}} 3 2 \bm{\textcolor{blue}{2}} 2 5 \bm{\textcolor{red}{5}} 5 1 \bm{\textcolor{black}{1}} 1
  • 第四次比较： 5 > 1 5 > 1 5>1 ，关键字 逆序 ，需要执行 交换
下标 0 1 2 3 4
交换前： 4 \bm{\textcolor{black}{4}} 4 3 \bm{\textcolor{black}{3}} 3 2 \bm{\textcolor{black}{2}} 2 5 \bm{\textcolor{red}{5}} 5 1 \bm{\textcolor{blue}{1}} 1
交换后： 4 \bm{\textcolor{black}{4}} 4 3 \bm{\textcolor{black}{3}} 3 2 \bm{\textcolor{black}{2}} 2 1 \bm{\textcolor{blue}{1}} 1 5 \bm{\textcolor{red}{5}} 5

此时我们就确定了 最大值 在 升序 中的位置；

2.3.3 第二轮冒泡

在第二轮 冒泡 中，由于我们已经确定了 4 4 4 这个下标的 关键字 ，因此我们此时只需要完成 3 3 3 次 比较 ，即从 0 下标开始到 3 下标结束；

  • 第一次比较： 4 > 3 4 > 3 4>3 ，关键字 逆序 ，需要执行 交换
下标 0 1 2 3 4
交换前： 4 \bm{\textcolor{red}{4}} 4 3 \bm{\textcolor{blue}{3}} 3 2 \bm{\textcolor{black}{2}} 2 1 \bm{\textcolor{black}{1}} 1 5 \bm{\textcolor{black}{5}} 5
交换后： 3 \bm{\textcolor{blue}{3}} 3 4 \bm{\textcolor{red}{4}} 4 2 \bm{\textcolor{black}{2}} 2 1 \bm{\textcolor{black}{1}} 1 5 \bm{\textcolor{black}{5}} 5
  • 第二次比较： 4 > 2 4 > 2 4>2 ，关键字 逆序 ，需要执行 交换
下标 0 1 2 3 4
交换前： 3 \bm{\textcolor{black}{3}} 3 4 \bm{\textcolor{red}{4}} 4 2 \bm{\textcolor{blue}{2}} 2 1 \bm{\textcolor{black}{1}} 1 5 \bm{\textcolor{black}{5}} 5
交换后： 3 \bm{\textcolor{black}{3}} 3 2 \bm{\textcolor{blue}{2}} 2 4 \bm{\textcolor{red}{4}} 4 1 \bm{\textcolor{black}{1}} 1 5 \bm{\textcolor{black}{5}} 5
  • 第三次比较： 4 > 1 4 > 1 4>1 ，关键字 逆序 ，需要执行 交换
下标 0 1 2 3 4
交换前： 3 \bm{\textcolor{black}{3}} 3 2 \bm{\textcolor{black}{2}} 2 4 \bm{\textcolor{red}{4}} 4 1 \bm{\textcolor{blue}{1}} 1 5 \bm{\textcolor{black}{5}} 5
交换后： 3 \bm{\textcolor{black}{3}} 3 2 \bm{\textcolor{black}{2}} 2 1 \bm{\textcolor{blue}{1}} 1 4 \bm{\textcolor{red}{4}} 4 5 \bm{\textcolor{black}{5}} 5

此时我们再一次确定了 未排序元素中的最大值 在 升序 中的位置；

2.3.4 第三轮冒泡

在第二轮 冒泡 中，由于我们已经确定了 3 、 4 3、4 3、4 这个两个下标的 关键字 ，因此我们此时只需要完成 2 2 2 次 比较 ，即从 0 下标开始到 2 下标结束；

  • 第一次比较： 3 > 2 3 > 2 3>2 ，关键字 逆序 ，需要执行 交换
下标 0 1 2 3 4
交换前： 3 \bm{\textcolor{red}{3}} 3 2 \bm{\textcolor{blue}{2}} 2 1 \bm{\textcolor{black}{1}} 1 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{black}{5}} 5
交换后： 2 \bm{\textcolor{blue}{2}} 2 3 \bm{\textcolor{red}{3}} 3 1 \bm{\textcolor{black}{1}} 1 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{black}{5}} 5
  • 第二次比较： 3 > 1 3 > 1 3>1 ，关键字 逆序 ，需要执行 交换
下标 0 1 2 3 4
交换前： 2 \bm{\textcolor{black}{2}} 2 3 \bm{\textcolor{red}{3}} 3 1 \bm{\textcolor{blue}{1}} 1 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{black}{5}} 5
交换后： 2 \bm{\textcolor{black}{2}} 2 1 \bm{\textcolor{blue}{1}} 1 3 \bm{\textcolor{red}{3}} 3 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{black}{5}} 5

此时我们再一次确定了 未排序元素中的最大值 在 升序 中的位置；

2.3.5 第四轮冒泡

在第三轮 冒泡 中，由于我们已经确定了 2 、 3 、 4 2、3、4 2、3、4 这个三个下标的 关键字 ，因此我们此时只需要完成 1 1 1 次 比较 ，即从 0 下标开始到 1 下标结束；

  • 第一次比较： 2 > 1 2 > 1 2>1 ，关键字 逆序 ，需要执行 交换
下标 0 1 2 3 4
交换前： 2 \bm{\textcolor{red}{2}} 2 1 \bm{\textcolor{blue}{1}} 1 3 \bm{\textcolor{black}{3}} 3 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{black}{5}} 5
交换后： 1 \bm{\textcolor{blue}{1}} 1 2 \bm{\textcolor{red}{2}} 2 3 \bm{\textcolor{black}{3}} 3 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{black}{5}} 5

此时我们就完成了全部元素的 升序排列 ，大家可以通过下图更直观的感受整个 冒泡 的过程：

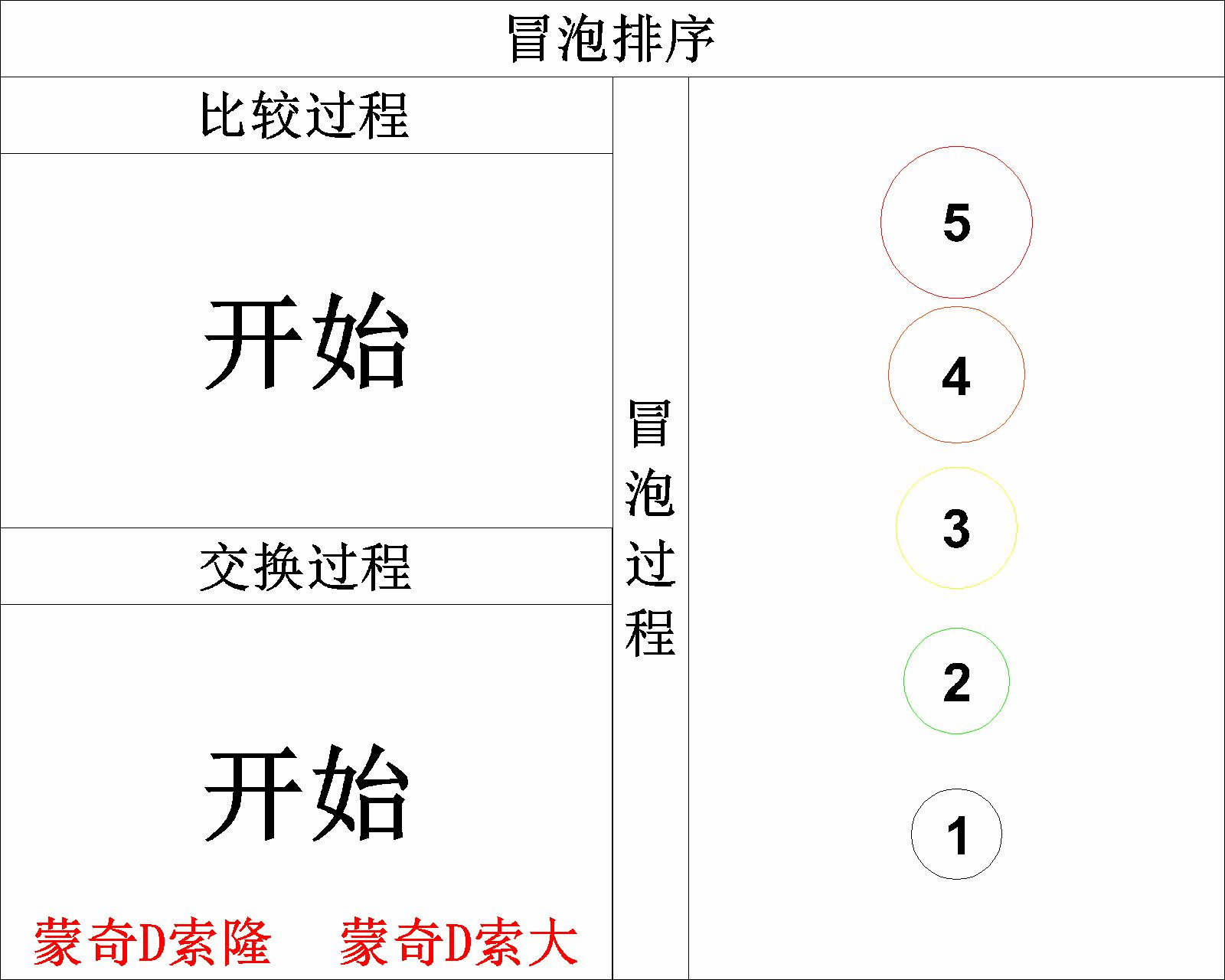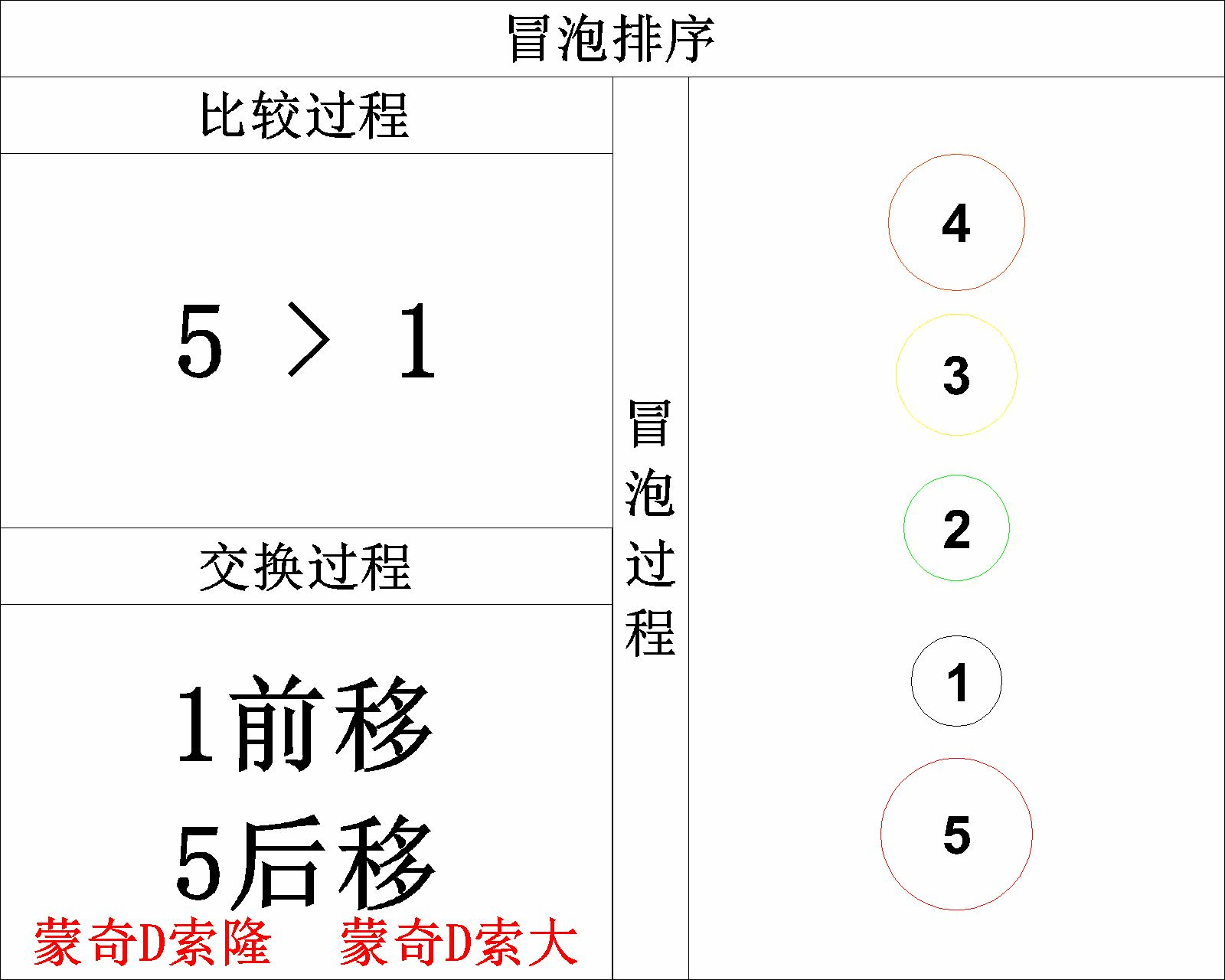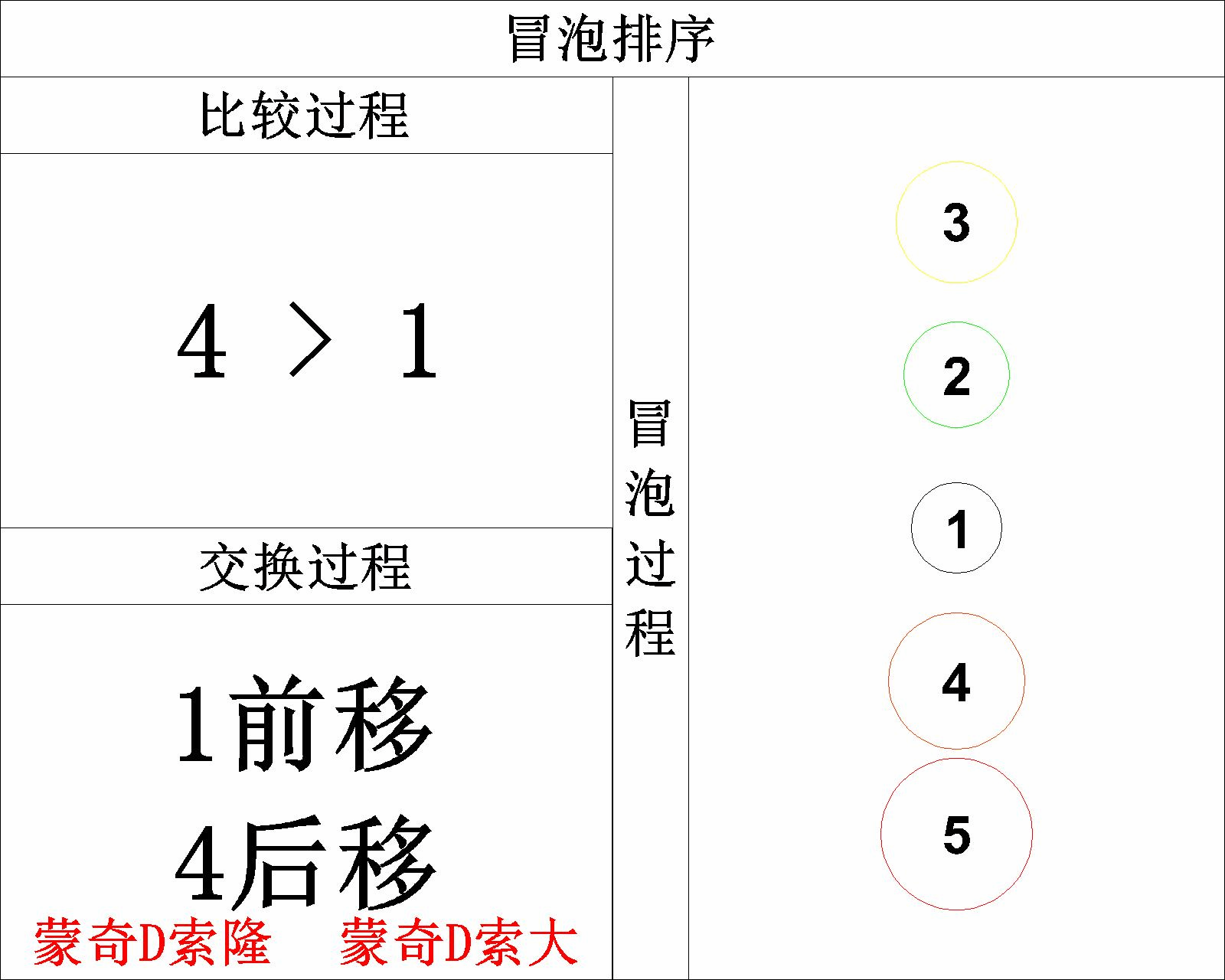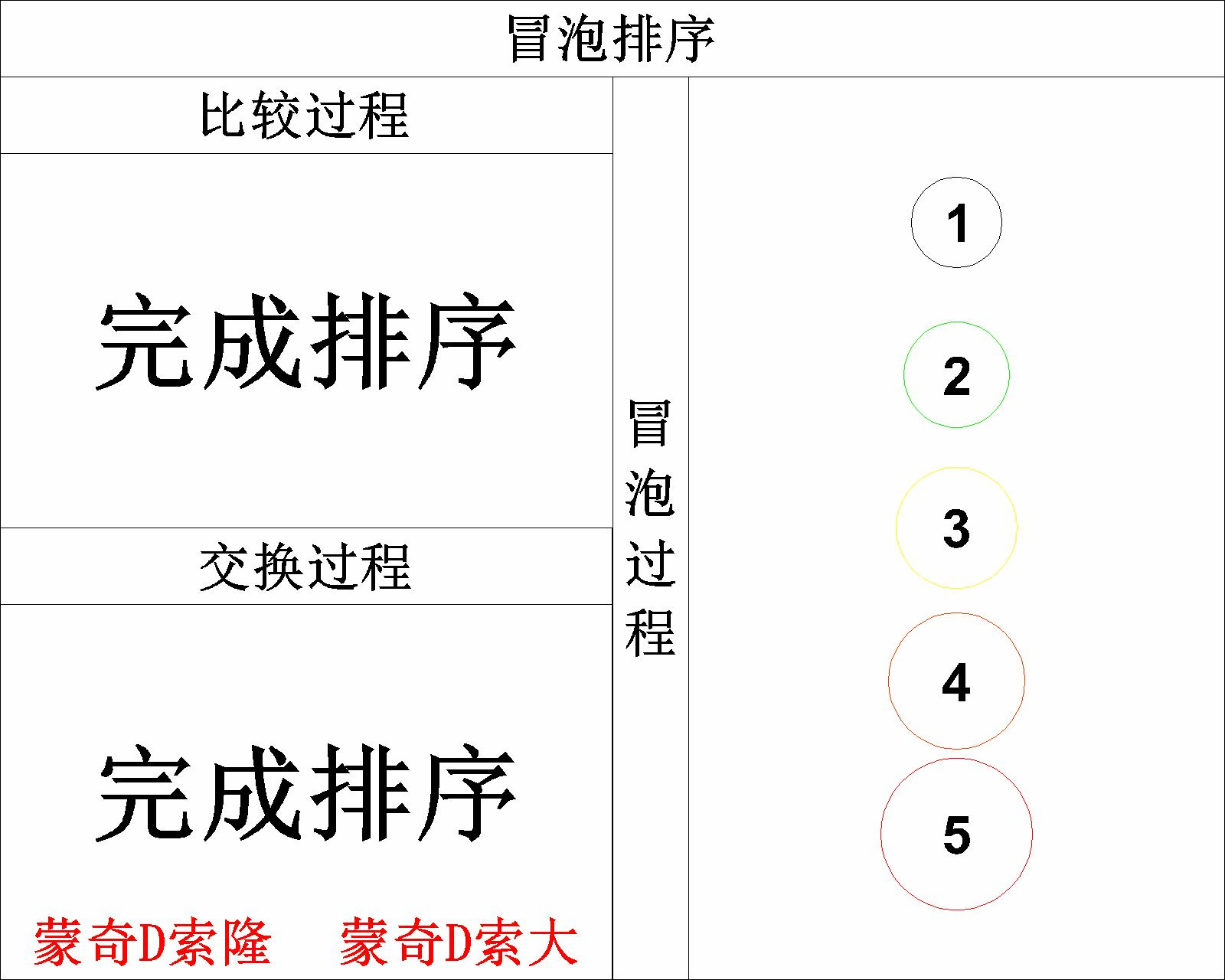
2.4 C语言实现

相信大家此时应该都已经对 冒泡排序 的整体过程不再陌生了，接下来我们就来一步一步的完成算法的C语言代码编写；

2.4.1 准备工作

在实现 冒泡排序 之前，我们需要先创建好三个文件：

  • 排序算法头文件 Bubble_Sort.h ------ 用于进行排序算法的声明
  • 排序算法实现文件 Bubble_Sort.c ------ 用于实现排序算法
  • 排序算法测试文件 text.c ------ 用于测试排序算法

2.4.2 函数三要素

与 插入排序算法 一样，冒泡排序 同样只需要知道排序的目标，以及排序目标的大小，因此我们还是参考 插入排序算法 来定义 函数三要素：

c 复制代码 
// 交换排序------冒泡排序
void BubbleSort(ElemType* nums, int len) {

}

2.4.3 冒泡次数

在 冒泡排序 中，对于 N N N 个 关键字 的序列，我们就需要执行 N − 1 N -1 N−1 轮冒泡，并且在每一轮冒泡中确定一个 关键字 的具体位置；

c 复制代码 
	// 冒泡次数
	for (int i = 1; i < len; i++) {

	}

2.4.4 一次冒泡的比较次数

在 冒泡排序 中，我们可以将 关键字序列 分为两部分：
冒泡元素
待比较元素序列

那也就是说，此时有 N N N 个元素等待着排序，那么有 1 1 1 个元素就是 冒泡元素 ，而剩余的 N − 1 N -1 N−1 个元素就组成了 待比较元素序列 。因此，在 第一次冒泡 中，总共需要执行 N − 1 N - 1 N−1 次的 比较操作 ；

随着每一次冒泡的执行，都会确定一个元素的具体位置 ，因此 冒泡 的比较次数也会相比于前一次要少 1 \bm{1} 1 。根据这个思路，那么对应的C语言代码就应该是：

c 复制代码 
		// 一轮冒泡的比较次数
		for (int j = 0; j <= len - i - 1; j++) {

		}

这里我们是实现的 从前往后冒泡 ，也就是从 0 下标开始，直到 len - 2 下标为止。

这里可能有朋友会有疑问，为什么是 len - i - 1 而不是 len - 2？

这个问题也很好理解：

  • 随着每一次冒泡，都会确定一个元素的位置，即：
下标 0 1 ⋯ \cdots ⋯ len - 2 len - 1
第一次冒泡 F a l s e \textcolor{black}{False} False F a l s e \textcolor{black}{False} False ⋯ \cdots ⋯ F a l s e \textcolor{black}{False} False T r u e \textcolor{red}{True} True
第二次冒泡 F a l s e \textcolor{black}{False} False F a l s e \textcolor{black}{False} False ⋯ \cdots ⋯ T r u e \textcolor{red}{True} True T r u e \textcolor{red}{True} True
⋮ \vdots ⋮ ⋮ \vdots ⋮ ⋮ \vdots ⋮ ⋯ \cdots ⋯ ⋮ \vdots ⋮ ⋮ \vdots ⋮
第 l e n − 2 len - 2 len−2 次冒泡 F a l s e \textcolor{black}{False} False T r u e \textcolor{red}{True} True ⋯ \cdots ⋯ T r u e \textcolor{red}{True} True T r u e \textcolor{red}{True} True
第 l e n − 1 len - 1 len−1 次冒泡 T r u e \textcolor{red}{True} True T r u e \textcolor{red}{True} True ⋯ \cdots ⋯ T r u e \textcolor{red}{True} True T r u e \textcolor{red}{True} True
  • 随着冒泡次数的增加，我们是不需要每一次都走到 len - 2 这个位置处，即 结束下标会前移：
下标 0 1 2 ⋯ \cdots ⋯ len - 3 len - 2 len - 1
第一次冒泡 ⋯ \cdots ⋯ 结束下标 \textcolor{red}{结束下标} 结束下标 确定元素 \textcolor{blue}{确定元素} 确定元素
第二次冒泡 ⋯ \cdots ⋯ 结束下标 \textcolor{red}{结束下标} 结束下标 确定元素 \textcolor{blue}{确定元素} 确定元素 确定元素 \textcolor{black}{确定元素} 确定元素
⋮ \vdots ⋮ ⋮ \vdots ⋮ ⋮ \vdots ⋮ ⋮ \vdots ⋮ ⋯ \cdots ⋯ ⋮ \vdots ⋮ ⋮ \vdots ⋮ ⋮ \vdots ⋮
第 l e n − 2 len - 2 len−2 次冒泡 结束下标 \textcolor{red}{结束下标} 结束下标 确定元素 \textcolor{blue}{确定元素} 确定元素 ⋯ \cdots ⋯ 确定元素 \textcolor{black}{确定元素} 确定元素 确定元素 \textcolor{black}{确定元素} 确定元素 确定元素 \textcolor{black}{确定元素} 确定元素
第 l e n − 1 len - 1 len−1 次冒泡 结束下标 \textcolor{red}{结束下标} 结束下标 确定元素 \textcolor{blue}{确定元素} 确定元素 确定元素 \textcolor{black}{确定元素} 确定元素 ⋯ \cdots ⋯ 确定元素 \textcolor{black}{确定元素} 确定元素 确定元素 \textcolor{black}{确定元素} 确定元素 确定元素 \textcolor{black}{确定元素} 确定元素

可以看到，结束下标 的值就等于 元素总个数 − - − 冒泡的次数 − 1 - 1 −1，即 e n d i = l e n − i − 1 end_i = len - i - 1 endi=len−i−1

当然，我们也可以选择 从后往前冒泡 ，即从 len - 1 下标处开始，到 1 下标结束。对应代码如下所示：

c 复制代码 
	// 从后往前冒泡
	for (int i = 1; i < len; i++) {
		for (int j = len - 1; j >= i; j--) {

		}
	}

具体如何选择，这就需要看自己的需求；

2.4.5 交换操作

冒泡排序 是基于 交换排序思想 实现的排序算法，因此，其核心步骤一定有两种操作：

  • 比较操作 ：通过 比较 确定元素间的位置关系
  • 交换操作 ：通过 交换 实现 逆序 元素的位置互换，使其恢复 正序

因此 交换操作 的实现是我们一定需要掌握的。

相比于 折半插入排序 和 希尔排序 ，冒泡排序 并没有使用上的限制，它既可以用于 顺序表 的排序，又可以用于 链表 的排序，因此，其 交换操作 在不同的对象中，也有不同的实现方式：

c 复制代码 
			LNode* p;					// 冒泡结点
			LNode* pre;					// 直接前驱
			LNode* suc;					// 直接后继
			// 判断元素是否逆序
			if (p->data > suc->data) {
				// 方法一：基于链表的交换操作
				pre->next = suc;		// 直接前驱指向直接后继
				p->next = suc->next;	// 冒泡结点指针指向原直接后继的直接后继
				suc->next = p;			// 原直接后继的后继指针指向冒泡结点
			}
			// 判断元素是否逆序
			if (nums[j] > nums[j + 1]) {
				// 方法二：基于顺序表的交换操作
				ElemType* tmp = nums[j];
				nums[j] = nums[j + 1];
				nums[j + 1] = tmp;
			}

当然，若 链表结点 的 数据域 比较简单，那么我们同样可以参照 顺序表 的 交换操作 实现 链表的交换：

c 复制代码 
			// 判断元素是否逆序
			if (p->data > suc->data) {
				// 方法三：参照顺序表实现的链表交换
				ElemType tmp = p->data;
				p->data = suc->data;
				suc->data = tmp;
			}

因此我们在具体的实现中选择何种交换方式，这就需要看我们的具体需求：

  • 对 链表 进行 冒泡排序 ：
    • 凸显出交换的过程 ：选择 方法一
    • 凸显排序过程 ：选择 方法三
  • 对 顺序表 进行 冒泡排序 ：选择 方法二

2.4.6 性能分析

  • 空间效率 ：冒泡排序 仅使用了 ElemType 大小的空间来记录 待冒泡元素 ，因此其 空间复杂度 为 O ( 1 ) O(1) O(1)

  • 时间效率 ：当前我们实现的 冒泡排序 与 关键字序列 的初始状态无关，都需要执行 N − 1 N -1 N−1 次冒泡，每一次冒泡的比较次数为：

冒泡次数 比较次数
1 1 1 N − 1 N - 1 N−1
2 2 2 N − 2 N - 2 N−2
3 3 3 N − 3 N - 3 N−3
⋮ \vdots ⋮ ⋮ \vdots ⋮
N − 2 N -2 N−2 2 2 2
N − 1 N - 1 N−1 1 1 1

即，总的比较次数为：

( N − 1 ) + ( N − 2 ) + ( N − 3 ) + ⋯ + 2 + 1 = ( ( N − 1 ) + 1 ) ∗ ( N − 1 ) 2 = N 2 − N 2 \begin{align*} &\enspace\enspace (N - 1) + (N - 2) + (N - 3) + \cdots + 2 + 1 \\ &= \frac{((N-1) + 1) * (N - 1)}{2} \\ &= \frac{N^2 - N}{2} \end{align*} (N−1)+(N−2)+(N−3)+⋯+2+1=2((N−1)+1)∗(N−1)=2N2−N

因此当前我们实现的冒泡排序的 时间复杂度 为 O ( N 2 ) O(N^2) O(N2)

  • 稳定性 ：冒泡排序 的 交换逻辑 为 nums[j] > nums[j + 1] ，这也就表示，当 nums[j] == nums[j + 1] 时并不会执行 交换操作 ，因此 冒泡排序 是一种 稳定排序算法；

  • 适用性 ：冒泡排序 既适用于 顺序表 也适用于 链表；

2.4.7 算法优化

对于当前我们实现的 冒泡排序 会存在一个问题：

  • 当 关键字序列初始已经正序 时，我们同样还是会进行 N 2 − N 2 \frac{N^2 - N}{2} 2N2−N 次比较

这个问题显然是不合理的，那我们应该如何规避呢？

很简单，我们只需要设置一个 交换标志 ，来记录本次是否执行了 交换操作 ，这样我们就能够在某一次 冒泡中 为执行 交换 时提前结束循环，如下所示：

c 复制代码 
	// 冒泡次数
	for (int i = 1; i < len; i++) {
		// 交换标志
		bool flag = false;
		// 一轮冒泡的比较次数
		for (int j = 0; j <= len - i - 1; j++) {
			// 判断元素是否逆序
			if (nums[j] > nums[j + 1]) {
				// 方法二：基于顺序表的交换操作
				ElemType* tmp = nums[j];
				nums[j] = nums[j + 1];
				nums[j + 1] = tmp;
				flag = true;
			}
		}
		if (flag == false) {
			break;
		}
	}

这里可能有朋友不太明白为什么可以通过 交换标志 来判断，这里我们简单的说明一下；

冒泡排序并不是说以某一个元素为基准开始执行的排序操作，而是仅关注当前比较的两个元素，如下所示：

下标 0 1 2 3 4
初始状态： 1 \bm{\textcolor{red}{1}} 1 3 \bm{\textcolor{blue}{3}} 3 2 \bm{\textcolor{black}{2}} 2 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{black}{5}} 5

当我们在第一次冒泡中，同样会执行 4 4 4 次比较：

  • 第一次比较： 1 < 3 1 < 3 1<3 ，元素 正序，不执行任何操作：
下标 0 1 2 3 4
比较前： 1 \bm{\textcolor{red}{1}} 1 3 \bm{\textcolor{blue}{3}} 3 2 \bm{\textcolor{black}{2}} 2 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{black}{5}} 5
比较后： 1 \bm{\textcolor{red}{1}} 1 3 \bm{\textcolor{blue}{3}} 3 2 \bm{\textcolor{black}{2}} 2 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{black}{5}} 5
  • 第二次比较： 3 > 2 3 > 2 3>2 ，元素 逆序 ，进行 交换
下标 0 1 2 3 4
比较前： 1 \bm{\textcolor{black}{1}} 1 3 \bm{\textcolor{red}{3}} 3 2 \bm{\textcolor{blue}{2}} 2 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{black}{5}} 5
比较后： 1 \bm{\textcolor{black}{1}} 1 2 \bm{\textcolor{blue}{2}} 2 3 \bm{\textcolor{red}{3}} 3 4 \bm{\textcolor{black}{4}} 4 5 \bm{\textcolor{black}{5}} 5
  • 第三次比较： 3 < 4 3 < 4 3<4 ，元素 正序，不执行任何操作：
下标 0 1 2 3 4
比较前： 1 \bm{\textcolor{black}{1}} 1 2 \bm{\textcolor{black}{2}} 2 3 \bm{\textcolor{red}{3}} 3 4 \bm{\textcolor{blue}{4}} 4 5 \bm{\textcolor{black}{5}} 5
比较后： 1 \bm{\textcolor{black}{1}} 1 2 \bm{\textcolor{black}{2}} 2 3 \bm{\textcolor{red}{3}} 3 4 \bm{\textcolor{blue}{4}} 4 5 \bm{\textcolor{black}{5}} 5
  • 第四次比较： 4 < 5 4 < 5 4<5 ，元素 正序，不执行任何操作：
下标 0 1 2 3 4
比较前： 1 \bm{\textcolor{black}{1}} 1 2 \bm{\textcolor{black}{2}} 2 3 \bm{\textcolor{black}{3}} 3 4 \bm{\textcolor{red}{4}} 4 5 \bm{\textcolor{blue}{5}} 5
比较后： 1 \bm{\textcolor{black}{1}} 1 2 \bm{\textcolor{black}{2}} 2 3 \bm{\textcolor{black}{3}} 3 4 \bm{\textcolor{red}{4}} 4 5 \bm{\textcolor{blue}{5}} 5

这个过程中，我们需要关注的是 标红 字体。可以看到当未执行 交换操作 时，标红字体 所标注的 冒泡元素 会发生改变，而不是像我们前面的演示例子中一样一直不变。

因此当一轮 冒泡 走完，没有出现 交换 操作，那就表示当前的 关键字序列 已经 正序 ，我们也就不用继续 冒泡 ；

当我们通过加入 交换标记 后，冒泡排序 的算法时间效率在 最好情况下 就可以下降到： O ( N ) O(N) O(N) 这个数量级，即，只需要完成一趟冒泡即可；

2.4.8 算法代码

完整代码如下所示：

c 复制代码 
// 算法头文件
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>
#include <time.h>
typedef int ElemType;
// 交换排序------冒泡排序
void BubbleSort(ElemType* nums, int len);
// 插入排序------希尔排序
void ShellSort(ElemType* nums, int len);
// 插入排序------折半插入排序
void BInsertSort(ElemType* nums, int len);
// 插入排序------直接插入排序
void InsertSort(ElemType* a, int len);
// 数组打印
void Print(ElemType* arr, int len);
// 折半插入排序测试
void test();

// 算法实现文件
#include "Bubble_Sort.h"

// 交换排序------冒泡排序
void BubbleSort(ElemType* nums, int len) {
	// 冒泡次数
	for (int i = 1; i < len; i++) {
		// 交换标志
		bool flag = false;
		// 一轮冒泡的比较次数
		for (int j = 0; j <= len - i - 1; j++) {
			// 判断元素是否逆序
			if (nums[j] > nums[j + 1]) {
				// 方法二：基于顺序表的交换操作
				ElemType* tmp = nums[j];
				nums[j] = nums[j + 1];
				nums[j + 1] = tmp;
				flag = true;
			}
		}
		if (flag == false) {
			break;
		}
	}
}

// 插入排序------希尔排序
void ShellSort(ElemType* nums, int len) {
	// 第一层划分
	for (int d = len / 2; d >= 1; d /= 2) {
		// 第二层划分
		for (int i = 0; i < len - d; i++) {
			ElemType key = nums[i + d];	// 记录待插入元素
			// 查找与移动
			int j = i;	// 待插入元素下标
			while (j >= 0 && nums[j] > key) {
				nums[j + d] = nums[j];
				j -= d;
			}
			// 插入
			nums[j + d] = key;
		}
	}
}

// 插入排序------折半插入排序
void BInsertSort(ElemType* nums, int len) {
	// 按左侧有序有边界进行划分
	for (int i = 0; i < len - 1; i++) {
		int key = nums[i + 1];	// 待排序对象
		// 折半查找
		int l = 0, r = i;	// 折半查找的左右指针
		while (l <= r) {
			int m = (r - l) / 2 + l;
			// 中间值 大于 目标值，目标值位于中间值左侧
			if (nums[m] > key) {
				r = m - 1;	// 更新右边界
			}
			// 中间值 小于等于 目标值，目标值位于中间值右侧
			else {
				l = m + 1;
			}
		}
		// 移动
		for (int j = i; j >= l; j--) {
			nums[j + 1] = nums[j];
		}
		// 插入
		nums[l] = key;
	}
}

//插入排序------直接插入排序
void InsertSort(ElemType* a, int len) {
	//以左侧有序对象的起点作为分界线对排序对象进行划分
	for (int i = 0; i < len - 1; i++) {
		//记录需要排序的元素
		ElemType key = a[i + 1];
		//插入位置的查找
		int j = i;//记录左侧有序元素的起点
		//j < 0时表示查找完左侧所有元素
		//a[j] <= key时表示找到了元素需要进行插入的位置
		while (j >= 0 && a[j] > key) {
			a[j + 1] = a[j];//元素向后移动
			j -= 1;//移动查找指针
		}
		//插入元素
		a[j + 1] = key;
	}
}

// 数组打印
void Print(ElemType* arr, int len) {
	printf("元素序列：");
	for (int i = 0; i < len; i++) {
		printf("%d\t", arr[i]);
	}
	printf("\n");
}

// 冒泡排序测试
void test() {
	ElemType* arr1 = (ElemType*)calloc(100000, sizeof(ElemType));
	assert(arr1);
	ElemType* arr2 = (ElemType*)calloc(100000, sizeof(ElemType));
	assert(arr2);
	ElemType* arr3 = (ElemType*)calloc(100000, sizeof(ElemType));
	assert(arr3);
	ElemType* arr4 = (ElemType*)calloc(100000, sizeof(ElemType));
	assert(arr4);
	ElemType* arr5 = (ElemType*)calloc(10, sizeof(ElemType));
	assert(arr5);
	// 设置伪随机数
	srand((unsigned)time(NULL));
	// 生成10w个随机数
	for (int i = 0; i < 100000; i++) {
		arr1[i] = rand() % 100000;
		arr2[i] = arr1[i];
		arr3[i] = arr1[i];
		arr4[i] = arr1[i];
		if (i < 10) {
			arr5[i] = rand() % 100;
		}
	}

	// 算法健壮性测试
	printf("\n排序前：");
	Print(arr5, 10);
	BubbleSort(arr5, 10);
	printf("\n排序后：");
	Print(arr5, 10);

	// 算法效率测试
	int begin1 = clock();
	InsertSort(arr1, 100000);
	int end1 = clock();
	double time_used1 = ((double)(end1 - begin1)) / CLOCKS_PER_SEC;
	printf("\n直接插入排序总耗时：%lf 秒\n", time_used1);

	int begin2 = clock();
	BInsertSort(arr2, 100000);
	int end2 = clock();

	double time_used2 = ((double)(end2 - begin2)) / CLOCKS_PER_SEC;
	printf("\n折半插入排序总耗时：%lf 秒\n", time_used2);

	int begin3 = clock();
	ShellSort(arr3, 100000);
	int end3 = clock();

	double time_used3 = ((double)(end3 - begin3)) / CLOCKS_PER_SEC;
	printf("\n    希尔排序总耗时：%lf 秒\n", time_used3);

	int begin4 = clock();
	BubbleSort(arr4, 100000);
	int end4 = clock();

	double time_used4 = ((double)(end4 - begin4)) / CLOCKS_PER_SEC;
	printf("\n    冒泡排序总耗时：%lf 秒\n", time_used4);

	free(arr1);
	arr1 = NULL;
	free(arr2);
	arr2 = NULL;
	free(arr3);
	arr3 = NULL;
	free(arr4);
	arr4 = NULL;
	free(arr5);
	arr5 = NULL;
}

// 算法测试文件
#include "Bubble_Sort.h"
int main() {
	test();
	return 0;
}

下面我们一起来看一下测试结果：

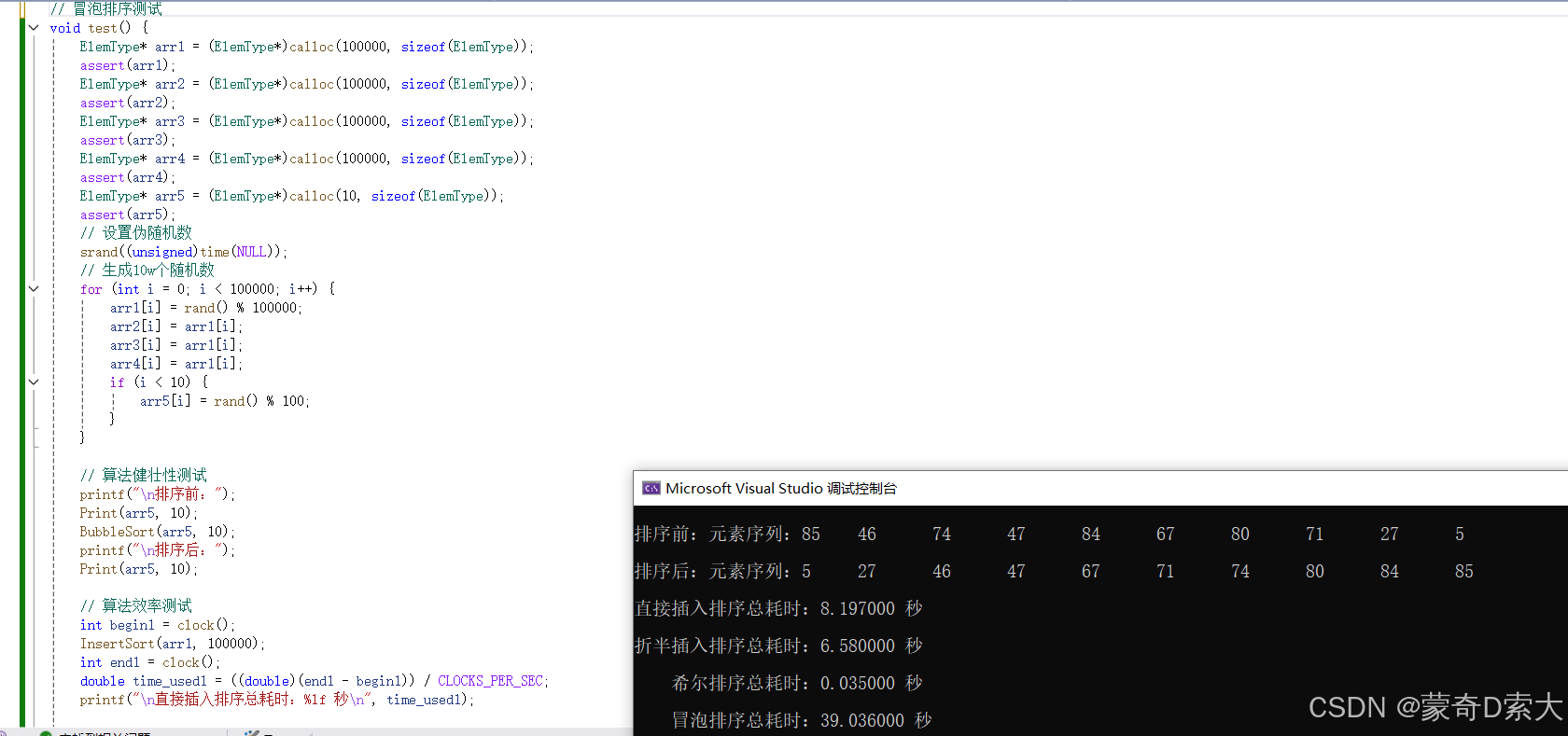
从这次测试中我们不难发现，相比于 直接插入排序 ，冒泡排序 的算法效率也不怎么高，这是不是说明 交换排序思想 不如 插入排序思想 呢？

那就让我们带着这个问题到下一篇内容中再进行解答；

结语

通过今天的学习，我们深入剖析了 交换排序 的基本思想，并完整探讨了其最直观的体现------冒泡排序 。我们看到，冒泡排序通过反复比较和交换相邻元素 ，像气泡上浮一样逐步将 极值归位 ，其过程生动展示了 交换作为排序核心动力 的运作方式。

尽管 冒泡排序 在最好情况下（序列已有序且使用优化标志 ）时间复杂度 可优化至 O ( N ) O(N) O(N)，但其平均与最坏情况时间复杂度均为 O ( N 2 ) O(N^2) O(N2)。这在处理大规模数据时效率较低，但其价值远不止于效率指标：

  • 算法基石：其实现简单，代码逻辑清晰，是理解排序算法入门概念的绝佳教学模型。

  • 稳定可靠：它是一种稳定的排序算法，在需要保持相等元素原始顺序的场景中至关重要。

  • 空间高效：作为原地排序算法，其空间复杂度为 O(1)，在内存空间受限的环境（如嵌入式系统）中仍有其用武之地。

文末我们曾提出一个核心问题：这是否意味着交换排序思想整体上不如插入排序思想 ？

然而，交换排序 的智慧并不仅限于 冒泡 这一种形式。事实上，冒泡排序 更像是 交换排序家族 的 先行者 ，它揭示了交换的核心操作，但远未展现该思想所能达到的效率巅峰 。

那么，交换排序思想 能否孕育出性能足以比肩、甚至超越高级插入排序（如希尔排序）的算法呢？ 交换这一基础操作，又能否像杠杆一样，撬动整个数据序列，迸发出远超我们当前认知的排序效率 ？

欲知后事如何，且听下回分解。我们下一篇再见分晓！

互动与分享

  • 点赞👍 - 您的认可是我持续创作的最大动力

  • 收藏⭐ - 方便随时回顾这些重要的基础概念

  • 转发↗️ - 分享给更多可能需要的朋友

  • 评论💬 - 欢迎留下您的宝贵意见或想讨论的话题

感谢您的耐心阅读！ 关注博主，不错过更多技术干货。我们下一篇再见！

相关推荐
sin_hielo2 小时前
leetcode 1351
数据结构·算法·leetcode
睡醒了叭2 小时前
图像分割-传统算法-边缘分割
图像处理·opencv·算法·计算机视觉
AndrewHZ2 小时前
【图像处理基石】有哪些好用的图像去噪算法可以推荐一下么？
图像处理·深度学习·算法·计算机视觉·cv·噪声
一叶知秋062 小时前
数据结构-什么是单向链表？
数据结构·链表
雪花desu2 小时前
【Hot100-Java中等】：字母异位词分组
java·算法·leetcode·哈希表
Bdygsl2 小时前
数据结构 —— 栈
数据结构
Word码2 小时前
LeetCode283. 移动零（双指针精讲）
算法·leetcode·职场和发展
编程之路，妙趣横生2 小时前
数据结构(十一) 哈希表
数据结构
客梦2 小时前
数据结构--队列
数据结构·笔记
热门推荐
01GitHub 镜像站点02从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击03电脑检测软件—图吧工具箱04Linux下V2Ray安装配置指南05Web安全中SQL注入绕过WAF的具体手法和实战案例06UV安装并设置国内源073D 圣诞树网页代码08jdk21下载、安装（Windows、Linux、macOS）09SQLmap 完整使用指南：环境搭建 + 命令详解 + 实操案例10BongoCat - 跨平台键盘猫动画工具