【数据结构】排序算法精讲 | 快速排序全解：高效实现、性能评估、实战剖析

C语言实现快排

• 导读
• 一、算法原理
• • [1.1 分治策略](#1.1 分治策略)
  • [1.2 快排中的分治策略](#1.2 快排中的分治策略)
• 二、C语言实现
• • [2.1 准备工作](#2.1 准备工作)
  • [2.2 函数三要素](#2.2 函数三要素)
  • [2.3 基准选择](#2.3 基准选择)
  • [2.4 分区](#2.4 分区)
  • • [2.4.1 移动控制](#2.4.1 移动控制)
    • [2.4.2 基准元素处理](#2.4.2 基准元素处理)
    • [2.4.3 相同元素处理](#2.4.3 相同元素处理)
  • [2.5 递归](#2.5 递归)
  • • [2.5.1 递归出口](#2.5.1 递归出口)
    • [2.5.2 边界处理](#2.5.2 边界处理)
  • [2.6 算法性能](#2.6 算法性能)
  • • [2.6.1 空间效率](#2.6.1 空间效率)
    • [2.6.2 时间效率](#2.6.2 时间效率)
    • [2.6.3 稳定性](#2.6.3 稳定性)
  • [2.7 算法代码](#2.7 算法代码)
• 结语

导读

大家好，很高兴又和大家见面啦！！！

在上一篇内容中我们介绍了 快速排序 的 基本思想 以及 排序步骤，这里我们简单的回顾一下：

• 快速排序 是结合了 比较排序 和 分治策略 的一种高效的 递归排序算法
• 快速排序 的排序过程可以总结为三步：
  • 基准选择 ：选择一个用于进行分区的 基准元素
  • 分区 ：通过 左右指针 的 交替扫描 与 元素交换 ，将小于基准的元素调整至其左侧，大于基准的元素调整至其右侧
  • 递归排序：将分区后的左右子序列作为新的待排序序列，重复上述过程，直至序列完全有序

了解了 快排 的 基本思想 以及 排序步骤 后，相信大家都会关心一个问题：

• 我们应该如何实现一个快速排序呢？

别着急，在今天的内容中，我们将会详细介绍 快排 的 C语言实现 以及 算法性能。下面就让我们进入今天的内容；

一、算法原理

快排 的 算法原理 是基于 分治策略，简单的说就是：

• 通过 双指针 将 关键字序列 进行 分区
• 每个分区所需要完成的任务与原序列的任务相同------实现 交换排序
• 通过 递归 对每个分区进行 快速排序 ，以达到从 局部有序 到 整体有序 的目的

可能有朋友并不太熟悉什么是 分治策略 这里我们简单的了解一下；

1.1 分治策略

分治策略 是一种非常重要的 算法设计思想 ，其 核心逻辑 可以概括为 分而治之：

• 将一个复杂的大问题分解成若干个规模较小、结构相似的子问题 ，然后分别解决这些子问题 ，最终将子问题的解合并起来得到原问题的解

也就是说 分治策略 包含 3 3 3 步 核心操作：

• 分解 ：将原问题划分为若干个 规模较小 、相互独立 、且 与原问题形式相同 的子问题。
  • 这里的 独立 是关键，它意味着子问题之间没有关联，可以分别求解，这为并行计算提供了可能
• 解决 ：递归地求解 各个子问题。
  • 如果子问题的规模已经足够小，可以直接求解时，则停止递归，直接进行求解。
• 合并 ：将各个子问题的解合并 ，最终形成原问题的解。
  • 有些算法的合并操作很简单（比如 快速排序 ），而有些则相对复杂（比如 归并排序）。

1.2 快排中的分治策略

在 快排 中，其 分治 的实现离不开 3 3 3 步操作：

• 双指针遍历 ：通过 双指针 将 关键字序列 分为 两部分 ：
  • 左侧小元素分区 ：基准元素左侧 的所有元素均 小于等于基准元素
  • 右侧大元素分区 ：基准元素右侧 的所有元素均 大于等于基准元素
• 交换排序 ：通过 交换排序 的两步核心操作来 解决排序问题 ：
  • 比较 ：通过 双指针 所指向的元素与 基准元素 的比较，确定 双指针 所指向的元素的 正确分区
  • 交换 ：通过 交换操作 将 双指针 所指向的元素放入 正确分区 中
• 递归 ：通过 递归 的两步核心操作来完成整个 分治策略 ：
  • 递进 ：通过 递进操作 实现 分治策略 中的 分而治之
  • 回归 ：通过 回归操作 实现 分治策略 中的 合并

因为 快排 是一种 原地排序算法 ，因此，其 合并操作 是一种 隐式合并：

• 没有明确直观的 分区合并 ，而是通过 分区边界恢复 实现的 合并

二、C语言实现

理解了 快排 的 算法原理 ，接下来我们就需要通过 C语言 逐步实现 快排；

2.1 准备工作

在实现 快速排序 之前，我们需要先创建好三个文件：

• 排序算法头文件 Quick_Sort.h ------ 用于进行排序算法的声明
• 排序算法实现文件 Quick_Sort.c ------ 用于实现排序算法
• 排序算法测试文件 text.c ------ 用于测试排序算法

2.2 函数三要素

快排 的作用是用于对 目标序列 进行 递归交换排序 ，因此我们需要明确 目标对象 、对象大小 ，作为一种 原地排序算法，函数也无需任何返回值，因此我们就可以参考之前的算法定义：

// 交换排序------快速排序
void Quick_Sort(ElemType* nums, int len) {

}

这时有朋友可能就会产生疑问：如果参数只有 nums, len 那我们应该如何确认分区呢？

如果你也有这种疑问，首先我要恭喜你，你现在已经意识到了 快排 的 核心 ------ 分区；

其次，我们需要知道 快排 的 适用范围 ------仅适用于顺序表；

最后，根据该 适用范围 我们就能够解释该定义下对 分区 的处理：

• 在 C语言 中，数组名 表示的是 数组首元素的地址 ，下标 表示的是 数组元素地址与数组首元素地址的差值 ，因此我们可以通过 数组 + 下标 的方式找到数组中以 下标 为 首元素 的 子数组 ，即 数组分区；

再简单一点说就是：

// 交换排序------快速排序
void QuickSort(ElemType* nums, int len) {
	QuickSort(nums, i); // 下标 0 ~ i - 1 的分区
	QuickSort(nums + i, len); // 下标 i ~ len - 1 的分区
}

现在大家看到这个代码应该就能够明白如何通过这两个参数进行 递归分区；

当然，我们也可以选择更加直观、可读性更强的方式进行定义：

// 交换排序------快速排序
void QuickSort(ElemType* nums, int begin, int end) {

}

这种定义方式就清楚的表明了 排序对象 、排序分区起点 、排序分区终点，这样我们就能一目了然，知道当前我们是在对哪一部分的分区进行排序操作；

具体如何选择，这个需要看个人的具体需求：

• 若想保证排序算法传参的一致性，则可以选择第一种
• 若想提高代码的可读性，则可以选择第二种

PS：下面我会采用第一种方式进行介绍，这也是为了后面对不同排序算法的对比分析更加方便；

2.3 基准选择

在 快排 中，我们需要做的第一件事就是------选择基准元素 ，这里我们选择以 首元素 作为基准元素，之后我们还需要记录当前的 基准元素：

	ElemType key = nums[0];					// 记录基准元素

2.4 分区

在 快排 中，我们是通过 双指针 实现的分区操作，因此我们需要先设置这两个指针，由于 快排 是用于 顺序表 的 原地排序算法 ，因此我们这里设置的 双指针 实际上就是 数组下标变量：

	int left = 0, right = len - 1;			// 设置双指针

这里需要注意，参数 len 这里在不同的情况下，其含义也不同：

• 当我们传入的 len 表示的是 分区元素总个数 时，那 右边界 对应的 数组下标 就是 len - 1；
• 当我们传入的 len 表示的是 右边界 时，那么对应的 数组下标 就是 len；

因为我这里的介绍要保持 排序函数接口的一致性 ，因此我这里的 len 表示的是 分区元素总个数；

整个分区的实现是通过 双指针 的 交替扫描 以及 比较 与 交换 操作实现，因此我们这里需要通过 循环 完成分区：

	// 分区
	while (left < right) {
		// 右指针寻找小值
		while (right > left && nums[right] > key) {
			right -= 1;
		}
		// 左指针寻找大值
		while (left < right && nums[left] <= key) {
			left += 1;
		}
		// 交换元素
		if (left < right) {
			Swap(&nums[left], &nums[right]);
		}
	}
	// 交换基准元素与当前指针指向元素
	Swap(&nums[left], &nums[0]);

2.4.1 移动控制

首先我们需要明确一件事：

• 交换操作 是发生 逆序 时才会执行

因此，双指针 的 交替查找 本质上就是在找 左右分区 中的 第一次逆序，因此才会出现下面的停止扫描现象：

• 当 右指针 扫描到 小于基准元素的元素 时，停止继续向左扫描
• 当 左指针 扫描到 大于基准元素的元素 时，停止继续向右扫描

这时在 扫描 的过程中就会出现一个问题：

• 当 左右指针 在 扫描 时，并未发现 逆序 ，指针就已经 相遇

当发生这种情况时，往往会导致出现 死循环 甚至是 数组越界 的问题，因此我们需要通过 左指针 小于 右指针 这个条件来 约束查找过程 ；

并且为了避免 重复交换 ，我们在 双指针 均完成 扫描 后，还需要保证 左指针 小于 右指针 这个前提，才能进行交换操作；

2.4.2 基准元素处理

在完成 扫描 后，此时 双指针 的相遇点一定是一个 关键字小于等于基准元素 的 元素 ，因此我们再执行一次 交换操作 ，就能够确保：

• 基准元素左侧所有元素均不大于基准元素，基准元素右侧均不小于基准元素

这里我们还需要注意的是 相同元素的处理 问题

2.4.3 相同元素处理

正常情况下我们都是采用的 左侧元素小于等于基准元素，右侧元素严格大于基准元素 的规则，将与 基准元素 相同的元素划分到 基准元素左侧分区 ；

当然，根据 快排 的具体实现方式的不同，我们还可以选择将 与基准元素相同的元素 划分到 基准元素右侧分区 。

这个问题我们在之后的内容中会继续详细介绍，这里我们就不再展开，我们现在只需要知道在本次的介绍中，我们采用的是第一种处理方式：

• 将与 基准元素 相同的元素划分到 基准元素左侧分区

2.5 递归

2.5.1 递归出口

由于 快排 是一种 递归排序算法 ，因此我们还需要按照 递归 的要求，设置一个 递归出口 ；

快排 的 递归出口 设置并不困难，我们只需要弄清其 递归 的目的即可：

• 递归 是为了对 元素个数大于1的分区 进行 排序 的操作

因此当此时 带查找 的分区中 不存在元素 或者 有且仅有一个元素 时，我们就无需继续 递归排序 。这样我们就得出了 递归出口：

• 分区内的元素个数满足 l e n ≤ 1 len \leq 1 len≤1

对应的代码如下：

	// 递归出口
	if (len <= 1) {
		return;
	}

在设置好了递归出口后，我们还需要明确 递归边界 ，即 递归排序的具体分区；

2.5.2 边界处理

前面我们也说过，快排 是一个适用于 顺序表 的 原地排序算法 ，因此我们可以通过 数组名 来确定 左边界 即 分区的起点 ，通过 元素总个数 来确定 右边界 即 分区终点：

	// 递归处理左侧分区
	QuickSort(nums, left);
	// 递归处理右侧分区
	QuickSort(nums + left + 1, len - left - 1);

我们知道 左侧分区 就是从 分区起点 到 基准元素 这个范围内的所有元素，而当我们完成了 分区 后，左指针 指向的区域正是 基准元素 ，因此 左侧分区 我们就可以通过 nums、left 来表示：

• nums 为 数组名 ，表示的是 数组的起始地址 ，因此代表 左侧分区 的 起点
• left 为 基准元素 此时所在的区域下标，同时也代表着 左侧分区 的 元素总个数 ，因此它也代表了 左侧分区 的 终点

相比于 左侧分区 ，右侧分区 的确定要稍微难一点，在我们当前的演示中，右侧分区 的 起点 应该是 基准元素 的右侧第一个元素，即下标为 left + 1 处的元素；而 分区终点 则是从 left + 1 这个下标开始，到 len 结束的这个区间内的 元素总个数 ，因此我们可以通过 下标之间的差值 来求出这个总个数，即 len - left - 1，这样我们就得到了具体的 右侧分区：

• nums + left + 1 为 右侧分区 的 起始地址 ，因此也代表 右侧分区 的 起点
• len - left - 1 为 右侧分区 的 元素总个数 ，因此也代表 右侧分区 的 终点

2.6 算法性能

此时我们就完成了 快排 的全部功能，接下来我们就需要分析一下该算法的具体 性能 ；

2.6.1 空间效率

快排 是一个 递归算法 ，因此每执行一次 递进 就需要在内存空间中开辟一块 函数栈帧 用于 算法执行 ，其 容量与递归的最大层数一致 。

根据 快排 的 算法特性：

• 左侧元素 < < < 基准元素 < < < 右侧元素

大家是否有一种 熟悉感 ？

没错，该特性正是与 BST 一致，也就是说我们可以将 快排 理解为通过 交换排序 构造 BST 的过程，当完成了所有元素的 排序操作 后，我们就得到了一棵 BST 。

因此，当我们构造的这个棵 BST 为一棵 平衡二叉树 时，那么对应的 树的深度 为 O ( log ⁡ 2 N ) O(\log_2 N) O(log2N)；当我们构造的这棵 BST极其不平衡 时，那么 BST 就会退化成一个 链表 ，对应的 树深 为 O ( N ) O(N) O(N)；

而 递归的深度 与 BST 的深度一致，因此我们就得到了整个 递归 的 空间复杂度：

• 最好空间复杂度： O ( log ⁡ 2 N ) O(\log_2N) O(log2N)
• 最坏空间复杂度： O ( N ) O(N) O(N)

2.6.2 时间效率

既然此时我们可以将 快排 的过程视为 构建BST 的过程，那么对应的 时间复杂度 实际上就是 BST 的 时间复杂度 ，即：

• 最好时间复杂度： O ( log ⁡ 2 N ) O(\log_2 N) O(log2N)
• 平均时间复杂度： O ( log ⁡ 2 N ) O(\log_2 N) O(log2N)
• 最坏时间复杂度： O ( N ) O(N) O(N)

但是 快排 又不是完全等同 BST ，对于 N N N 个元素的 关键字序列 ，我们总共需要执行 N N N 次 分区 ，即 每一次分区确定一个元素的位置 。因此 快排 的 时间复杂度 应该为：

• 最好时间复杂度： O ( N l o g 2 N ) O(Nlog_2N) O(Nlog2N)
• 平均时间复杂度： O ( N l o g 2 N ) O(Nlog_2N) O(Nlog2N)
• 最坏时间复杂度： O ( N 2 ) O(N^2) O(N2)

当从目前我们学习的 内部排序算法 来看，快排 的 平均性能 是 内部排序算法 最优的一种 原地排序算法；

2.6.3 稳定性

由于 快排 是通过 双指针 的 交替遍历 完成的 逻辑分区 ，对于 相同元素的处理，我们同样会根据具体情况执行不同的操作：

• 若规定 左侧分区小于等于基准元素 ，那么 遍历过程 中，右侧分区 中与 基准元素相等 的元素则会被 交换 到 左侧分区中
• 若规定 右侧分区大于等于基准元素 ，那么 遍历过程 中，左侧分区 中与 基准元素相等 的元素则会被 交换 到 右侧分区中

因此，不管如何规定，都会改变 相同元素的相对位置 ，这也就表明 快排是一种不稳定的排序算法；

2.7 算法代码

完整代码如下所示：

// 算法头文件
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>
#include <time.h>
#define N1 100000	// 大规模元素个数
#define N2 10		// 小规模元素个数
typedef int ElemType;
//交换操作
void Swap(ElemType* a, ElemType* b);
// 交换排序------快速排序
void QuickSort(ElemType* nums, int len);
// 交换排序------冒泡排序
void BubbleSort(ElemType* nums, int len);
// 插入排序------希尔排序
void ShellSort(ElemType* nums, int len);
// 插入排序------折半插入排序
void BInsertSort(ElemType* nums, int len);
// 插入排序------直接插入排序
void InsertSort(ElemType* a, int len);
// 数组打印
void Print(ElemType* arr, int len);
// 快速排序测试------随机数组测试
void test1();
// 快速排序测试------逆序数组测试
void test2();

// 算法实现文件
#include "Quick_Sort.h"

//交换操作
void Swap(ElemType* a, ElemType* b) {
	ElemType c = *a;
	*a = *b;
	*b = c;
}

// 交换排序------快速排序
void QuickSort(ElemType* nums, int len) {
	// 递归出口
	if (len <= 1) {
		return;
	}
	ElemType key = nums[0];					// 记录基准元素
	int left = 0, right = len - 1;			// 设置双指针
	// 分区
	while (left < right) {
		// 右指针寻找小值
		while (right > left && nums[right] > key) {
			right -= 1;
		}
		// 左指针寻找大值
		while (left < right && nums[left] <= key) {
			left += 1;
		}
		// 交换元素
		if (left < right) {
			Swap(&nums[left], &nums[right]);
		}
	}
	// 当跳出循环时，说明已经完成分区，此时交换基准元素与当前指针指向元素
	Swap(&nums[left], &nums[0]);
	// 递归处理左侧分区
	QuickSort(nums, left);
	// 递归处理右侧分区
	QuickSort(nums + left + 1, len - left - 1);
}

// 交换排序------冒泡排序
void BubbleSort(ElemType* nums, int len) {
	// 冒泡次数
	for (int i = 1; i < len; i++) {
		// 交换标志
		bool flag = false;
		// 一轮冒泡的比较次数
		for (int j = 0; j <= len - i - 1; j++) {
			// 判断元素是否逆序
			if (nums[j] > nums[j + 1]) {
				// 方法二：基于顺序表的交换操作
				ElemType tmp = nums[j];
				nums[j] = nums[j + 1];
				nums[j + 1] = tmp;
				flag = true;
			}
		}
		if (flag == false) {
			break;
		}
	}
}

// 插入排序------希尔排序
void ShellSort(ElemType* nums, int len) {
	// 第一层划分
	for (int d = len / 2; d >= 1; d /= 2) {
		// 第二层划分
		for (int i = 0; i < len - d; i++) {
			ElemType key = nums[i + d];	// 记录待插入元素
			// 查找与移动
			int j = i;	// 待插入元素下标
			while (j >= 0 && nums[j] > key) {
				nums[j + d] = nums[j];
				j -= d;
			}
			// 插入
			nums[j + d] = key;
		}
	}
}

// 插入排序------折半插入排序
void BInsertSort(ElemType* nums, int len) {
	// 按左侧有序有边界进行划分
	for (int i = 0; i < len - 1; i++) {
		int key = nums[i + 1];	// 待排序对象
		// 折半查找
		int l = 0, r = i;	// 折半查找的左右指针
		while (l <= r) {
			int m = (r - l) / 2 + l;
			// 中间值 大于 目标值，目标值位于中间值左侧
			if (nums[m] > key) {
				r = m - 1;	// 更新右边界
			}
			// 中间值 小于等于 目标值，目标值位于中间值右侧
			else {
				l = m + 1;
			}
		}
		// 移动
		for (int j = i; j >= l; j--) {
			nums[j + 1] = nums[j];
		}
		// 插入
		nums[l] = key;
	}
}

//插入排序------直接插入排序
void InsertSort(ElemType* a, int len) {
	//以左侧有序对象的起点作为分界线对排序对象进行划分
	for (int i = 0; i < len - 1; i++) {
		//记录需要排序的元素
		ElemType key = a[i + 1];
		//插入位置的查找
		int j = i;//记录左侧有序元素的起点
		//j < 0时表示查找完左侧所有元素
		//a[j] <= key时表示找到了元素需要进行插入的位置
		while (j >= 0 && a[j] > key) {
			a[j + 1] = a[j];//元素向后移动
			j -= 1;//移动查找指针
		}
		//插入元素
		a[j + 1] = key;
	}
}

// 数组打印
void Print(ElemType* arr, int len) {
	printf("元素序列：");
	for (int i = 0; i < len; i++) {
		printf("%d\t", arr[i]);
	}
	printf("\n");
}

// 快速排序测试------随机数组测试
void test1() {
	ElemType* arr1 = (ElemType*)calloc(	N1, sizeof(ElemType));
	assert(arr1);
	ElemType* arr2 = (ElemType*)calloc(N1, sizeof(ElemType));
	assert(arr2);
	ElemType* arr3 = (ElemType*)calloc(N1, sizeof(ElemType));
	assert(arr3);
	ElemType* arr4 = (ElemType*)calloc(N1, sizeof(ElemType));
	assert(arr4);
	ElemType* arr5 = (ElemType*)calloc(N1, sizeof(ElemType));
	assert(arr5);
	ElemType* arr6 = (ElemType*)calloc(N2, sizeof(ElemType));
	assert(arr6);
	// 设置伪随机数
	srand((unsigned)time(NULL));
	// 生成10w个随机数
	for (int i = 0; i < N1; i++) {
		arr1[i] = rand() % N1;
		arr2[i] = arr1[i];
		arr3[i] = arr1[i];
		arr4[i] = arr1[i];
		arr5[i] = arr1[i];
		if (i < N2) {
			arr6[i] = rand() % (N2 * 10);
		}
	}

	// 算法健壮性测试
	printf("\n排序前：");
	Print(arr6, N2);
	QuickSort(arr6, N2);
	printf("\n排序后：");
	Print(arr6, N2);

	printf("\n随机数组测试\n");
	// 算法效率测试
	int begin1 = clock();
	InsertSort(arr1, N1);
	int end1 = clock();
	double time_used1 = ((double)(end1 - begin1)) / CLOCKS_PER_SEC;
	printf("\n直接插入排序总耗时：%lf 秒\n", time_used1);

	int begin2 = clock();
	BInsertSort(arr2, N1);
	int end2 = clock();

	double time_used2 = ((double)(end2 - begin2)) / CLOCKS_PER_SEC;
	printf("\n折半插入排序总耗时：%lf 秒\n", time_used2);

	int begin3 = clock();
	ShellSort(arr3, N1);
	int end3 = clock();

	double time_used3 = ((double)(end3 - begin3)) / CLOCKS_PER_SEC;
	printf("\n    希尔排序总耗时：%lf 秒\n", time_used3);

	int begin4 = clock();
	BubbleSort(arr4, N1);
	int end4 = clock();

	double time_used4 = ((double)(end4 - begin4)) / CLOCKS_PER_SEC;
	printf("\n    冒泡排序总耗时：%lf 秒\n", time_used4);


	int begin5 = clock();
	QuickSort(arr5, N1);
	int end5 = clock();

	double time_used5 = ((double)(end5 - begin5)) / CLOCKS_PER_SEC;
	printf("\n    快速排序总耗时：%lf 秒\n", time_used5);

	free(arr1);
	arr1 = NULL;
	free(arr2);
	arr2 = NULL;
	free(arr3);
	arr3 = NULL;
	free(arr4);
	arr4 = NULL;
	free(arr5);
	arr5 = NULL;
	free(arr6);
	arr6 = NULL;
}

// 快速排序测试------逆序数组测试
void test2() {
	ElemType* arr1 = (ElemType*)calloc(N1, sizeof(ElemType));
	assert(arr1);
	ElemType* arr2 = (ElemType*)calloc(N1, sizeof(ElemType));
	assert(arr2);
	ElemType* arr3 = (ElemType*)calloc(N1, sizeof(ElemType));
	assert(arr3);
	ElemType* arr4 = (ElemType*)calloc(N1, sizeof(ElemType));
	assert(arr4);
	ElemType* arr5 = (ElemType*)calloc(N1, sizeof(ElemType));
	assert(arr5);
	ElemType* arr6 = (ElemType*)calloc(N2, sizeof(ElemType));
	assert(arr6);

	// 生成10w个降序排列数
	for (int i = 0; i < N1; i++) {
		arr1[i] = N1 - i;
		arr2[i] = arr1[i];
		arr3[i] = arr1[i];
		arr4[i] = arr1[i];
		arr5[i] = arr1[i];
		if (i < N2) {
			arr6[i] = N2 - i;
		}
	}

	// 算法健壮性测试
	printf("\n排序前：");
	Print(arr6, N2);
	QuickSort(arr6, N2);
	printf("\n排序后：");
	Print(arr6, N2);

	printf("\n逆序数组测试\n");
	// 算法效率测试
	int begin1 = clock();
	InsertSort(arr1, N1);
	int end1 = clock();
	double time_used1 = ((double)(end1 - begin1)) / CLOCKS_PER_SEC;
	printf("\n直接插入排序总耗时：%lf 秒\n", time_used1);

	int begin2 = clock();
	BInsertSort(arr2, N1);
	int end2 = clock();

	double time_used2 = ((double)(end2 - begin2)) / CLOCKS_PER_SEC;
	printf("\n折半插入排序总耗时：%lf 秒\n", time_used2);

	int begin3 = clock();
	ShellSort(arr3, N1);
	int end3 = clock();

	double time_used3 = ((double)(end3 - begin3)) / CLOCKS_PER_SEC;
	printf("\n    希尔排序总耗时：%lf 秒\n", time_used3);

	int begin4 = clock();
	BubbleSort(arr4, N1);
	int end4 = clock();

	double time_used4 = ((double)(end4 - begin4)) / CLOCKS_PER_SEC;
	printf("\n    冒泡排序总耗时：%lf 秒\n", time_used4);


	int begin5 = clock();
	QuickSort(arr5, N1);
	int end5 = clock();

	double time_used5 = ((double)(end5 - begin5)) / CLOCKS_PER_SEC;
	printf("\n    快速排序总耗时：%lf 秒\n", time_used5);

	free(arr1);
	arr1 = NULL;
	free(arr2);
	arr2 = NULL;
	free(arr3);
	arr3 = NULL;
	free(arr4);
	arr4 = NULL;
	free(arr5);
	arr5 = NULL;
	free(arr5);
	arr5 = NULL;
	free(arr6);
	arr6 = NULL;
}

// 算法测试文件
#include "Quick_Sort.h"

int main() {
	test1();
	test2();
	return 0;
}

下面我们一起来看一下测试结果：

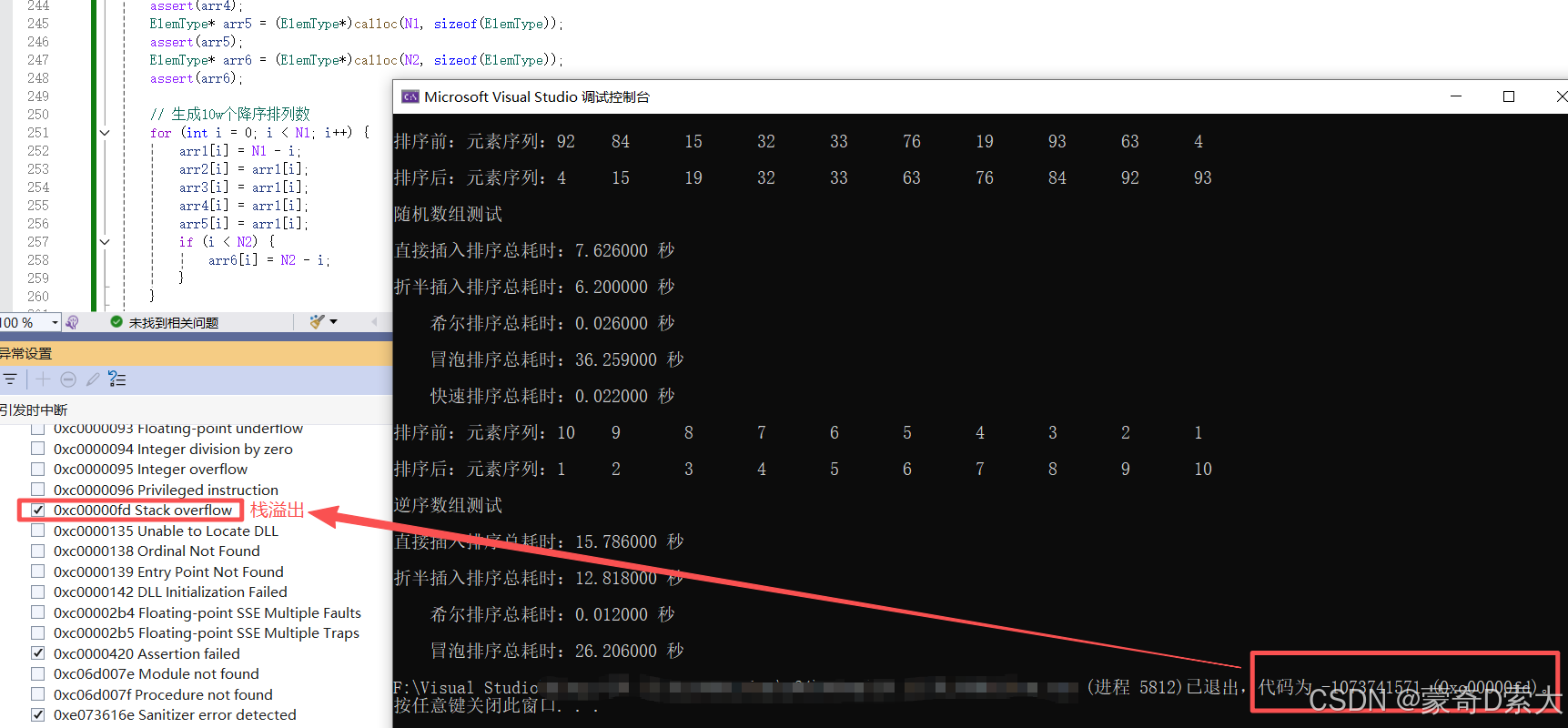
从这次测试结果中我们可以得到两个结论：

• 一般情况下，快速排序 要优于其他 排序算法
• 当原序列为 大规模 的 逆序序列 时，快排 会出现 栈溢出 的问题

显然 栈溢出 是目前 快排 的一个急需处理的问题，那么是什么原因导致的 栈溢出 呢？

这个问题的答案并不复杂，在前面我们也说过，快排 就像是一个 构建BST 的过程，因此在 最坏情况 下，快排 所构建的这棵 BST 是一个 长度 为 N N N 的 链表 。

这也就表示当前的递归的 递归深度 也为 N N N ，因此在大规模的情况下，就导致了 栈溢出 ；

那我们应该如何避免这个问题的出现呢？

其核心思路与 BST 的优化思路一致 ------ 使树尽量平衡，以此降低树的深度 。其具体方式有 随机数法 、三数取中法 、 ⋯ \cdots ⋯

其具体的优化方式我们将会在后续内容中揭晓，大家记得关注哦！

结语

在本文中，我们完成了 快速排序从理论到实践的完整跨越 ------不仅用C语言 实现了其 经典逻辑 ，还深入分析了其性能表现 与潜在缺陷 。

可以看出，快排 之所以高效，核心在于其 分治思想 与 原地交换 的巧妙结合，使其在平均情况下达到 O ( N log ⁡ 2 N ) O(N\log_2 N) O(Nlog2N) 的 时间复杂度，表现优异。

然而，我们的测试也暴露了一个关键问题：

• 当输入 序列已基本有序或完全逆序 时，基础版本的 快排 会退化为 O ( N 2 ) O(N^2) O(N2) ，递归深度急剧增加 ，甚至导致栈溢出。

这提醒我们，基准元素的选择 是 快排性能的决定性因素之一 ，而简单选取首元素作为基准的策略在真实场景中并不可靠。

那么，如何让快排变得更稳健、更高效？

这正是我们下一篇要探讨的核心------快排的优化策略 。

在下一篇内容中，我们将聚焦于 快速排序的优化策略。我们将探讨:

• 如何通过 更智能的基准选择方法（如随机数法和三数取中法）来避免最坏情况的发生
• 如何通过 结合插入排序 来处理小规模子数组以减少递归开销。

这些优化将共同作用，使 快速排序 从一个 理论高效 的算法，蜕变为一个在实践中同样稳定、强健的排序工具。

互动与分享

• 点赞👍 - 您的认可是我持续创作的最大动力

• 收藏⭐ - 方便随时回顾这些重要的基础概念

• 转发↗️ - 分享给更多可能需要的朋友

• 评论💬 - 欢迎留下您的宝贵意见或想讨论的话题

感谢您的耐心阅读！ 关注博主，不错过更多技术干货。我们下一篇再见！