在排序算法的大家族中,希尔排序是插入排序的 "进阶版",它通过引入 "增量" 概念,大幅提升了插入排序在大规模数据场景下的效率。本文将结合 C 语言代码实例,从原理、实现步骤到性能分析,带你全面掌握希尔排序。
一、希尔排序的核心原理:打破 "相邻比较" 的局限
要理解希尔排序,首先得回顾它的 "前身"------ 直接插入排序。直接插入排序的核心是 "将待排序元素插入到已排序序列的合适位置",但它只能逐个比较相邻元素,若数据逆序程度高(比如要把最小元素移到最前面),需要大量移动操作,时间复杂度高达 O (n²)。
希尔排序的改进思路很巧妙:先将整个数组按 "增量" 分成多个子数组,对每个子数组进行直接插入排序;然后逐步缩小增量,重复子数组排序操作;直到增量缩小为 1,此时对整个数组进行最后一次直接插入排序,算法结束。
这里的 "增量" 是关键:
- 初始增量通常取数组长度的一半(如数组长度为 10,初始增量为 5);
- 每次增量缩小为前一次的一半(5→2→1);
- 增量为 1 时,数组已基本有序,最后一次插入排序的效率会极高。
二、基于 C 语言的希尔排序实现(附代码解析)
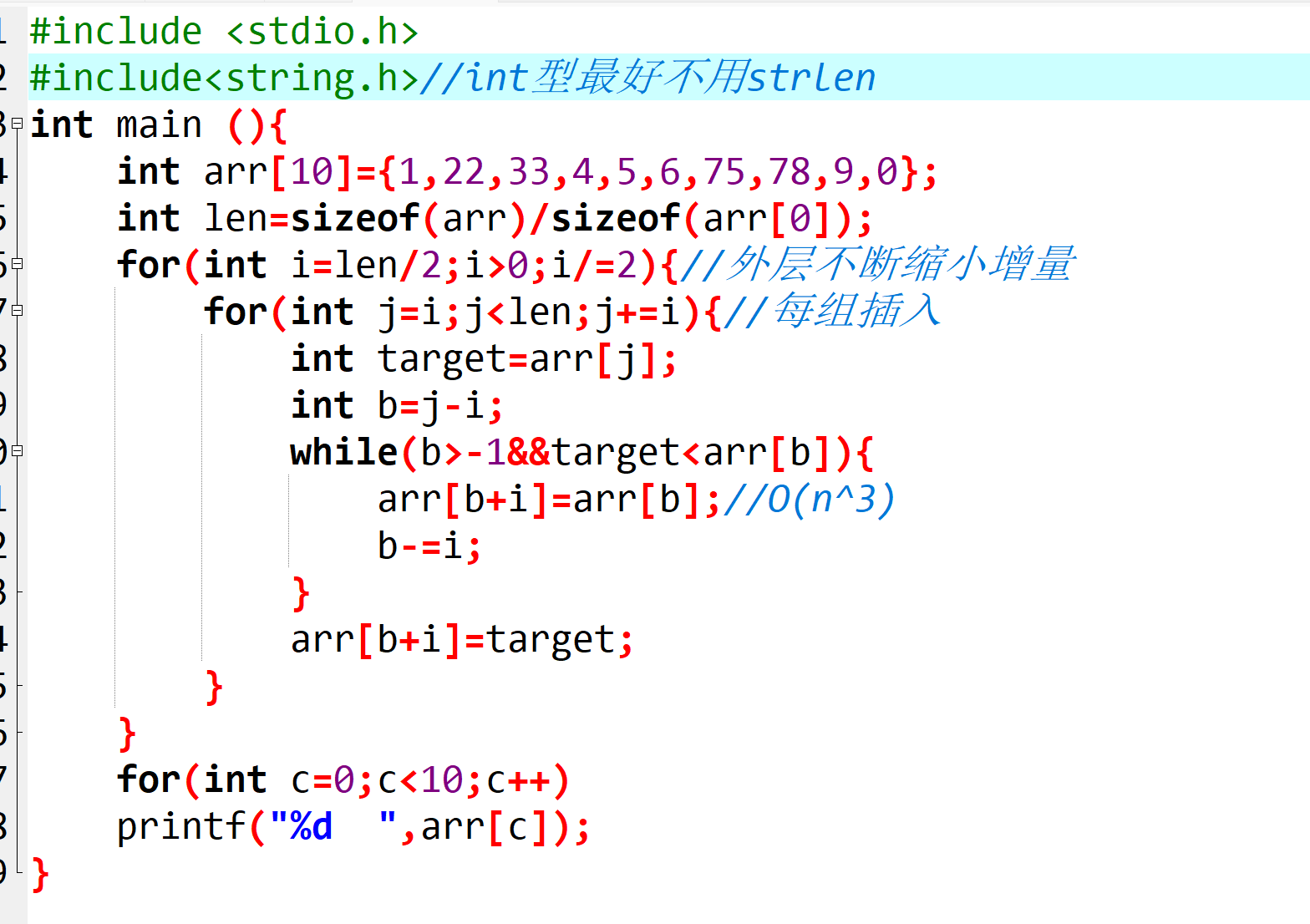
我们以你提供的代码为基础,逐行拆解希尔排序的实现逻辑。代码功能是对一个包含 10 个整数的数组进行排序,并打印结果。
1. 完整代码
#include <stdio.h>
#include <string.h> // 此处strlen未使用,可删除以优化代码
int main (){
// 1. 定义待排序数组
int arr[10]={1,22,33,4,5,6,75,78,9,0};
// 2. 计算数组长度(避免硬编码,提高通用性)
int len=sizeof(arr)/sizeof(arr[0]);
// 3. 希尔排序核心:外层循环控制增量缩小
for(int i=len/2;i>0;i/=2){ // 初始增量=len/2,每次减半,直到i=0时退出
// 4. 中层循环:按当前增量分组,遍历每组的待插入元素
for(int j=i;j<len;j+=i){ // j从增量位置开始,每次加增量遍历同组元素
// 5. 记录当前待插入的元素(避免后续移动时被覆盖)
int target=arr[j];
// 6. 内层循环:在当前子数组中,向前比较并移动元素
int b=j-i; // b是当前元素前一个同组元素的下标
// 当b>=0(未越界)且待插入元素小于前一个元素时,继续向前找
while(b>-1&&target<arr[b]){
arr[b+i]=arr[b]; // 将前一个元素向后移动增量位置
b-=i; // 继续向前遍历同组元素
}
// 7. 找到合适位置,插入待排序元素
arr[b+i]=target;
}
}
// 8. 打印排序后的数组
for(int c=0;c<10;c++)
printf("%d ",arr[c]);
return 0;
}
2. 关键步骤拆解
我们以数组arr[10] = {1,22,33,4,5,6,75,78,9,0}为例,结合增量变化,看排序过程:
步骤 1:初始增量 i=5(len/2=10/2=5)
此时数组按增量 5 分成 5 组:(arr[0],arr[5])、(arr[1],arr[6])、(arr[2],arr[7])、(arr[3],arr[8])、(arr[4],arr[9]),对每组进行直接插入排序:
- 组 1:[1,6] → 无需排序;
- 组 2:[22,75] → 无需排序;
- 组 3:[33,78] → 无需排序;
- 组 4:[4,9] → 无需排序;
- 组 5:[5,0] → 排序后为 [0,5];
- 第一次排序后数组:{1,22,33,4,0,6,75,78,9,5}。
步骤 2:增量 i=2(5/2=2,整数除法)
按增量 2 分成 2 组:(arr[0],arr[2],arr[4],arr[6],arr[8])、(arr[1],arr[3],arr[5],arr[7],arr[9]),每组插入排序:
- 组 1:[1,33,0,75,9] → 排序后为 [0,1,9,33,75];
- 组 2:[22,4,6,78,5] → 排序后为 [4,5,6,22,78];
- 第二次排序后数组:{0,4,1,5,9,6,33,22,75,78}。
步骤 3:增量 i=1(2/2=1)
此时增量为 1,对整个数组进行直接插入排序(数组已基本有序,仅需少量移动):
- 最终排序结果:{0,1,4,5,6,9,22,33,75,78}。
三、希尔排序的性能分析
希尔排序的性能不像直接插入排序(固定 O (n²))那样容易界定,它的时间复杂度与 "增量序列" 的选择密切相关,空间复杂度则非常稳定。
1. 时间复杂度
希尔排序的时间复杂度是非稳定的,取决于增量如何缩小:
- 最坏情况:若增量序列选择不当(如每次增量为前一次的 2 倍减 1),时间复杂度可能达到 O (n²)(但实际仍优于直接插入排序,因为数组提前被 "预处理" 为近似有序);
- 平均情况:在常用的 "增量 = len/2,每次减半" 策略下,平均时间复杂度约为O(n^1.3)(这是通过大量实验统计得出的结果,而非严格数学证明);
- 最优情况:若数组本身已有序,时间复杂度可接近 O (n)(仅需遍历,无需大量移动元素)。
需要注意的是,你代码中注释的 "O (n³)" 是错误的 ------ 内层 while 循环的执行次数随增量缩小而减少,整体嵌套循环的时间复杂度远低于 O (n³),实际应参考上述分析。
2. 空间复杂度
希尔排序是原地排序算法 ,仅需额外定义 3 个变量(len、target、b),与数组规模 n 无关,因此空间复杂度为O(1)。
3. 稳定性
希尔排序是不稳定排序。例如,数组{3, 3, 1}按增量 2 分组时,第一个 3(下标 0)和第二个 3(下标 1)会被分到不同组,排序后可能导致两个 3 的相对位置发生变化。
四、希尔排序的优化方向
你提供的代码已实现希尔排序的核心逻辑,但仍有优化空间:
- 优化增量序列:
目前使用的 "len/2" 增量序列虽然简单,但并非最优。更高效的增量序列如 "Hibbard 序列"(1, 3, 7, ..., 2^k-1)或 "Sedgewick 序列"(1, 5, 19, 41, ...),可将平均时间复杂度进一步降低到 O (n^1.2) 甚至更低。
- 删除无用头文件:
代码中#include <string.h>未使用(strlen用于字符串长度计算,与 int 数组无关),删除后可减少编译依赖。
- 增加通用性:
可将排序逻辑封装为函数(如void shellSort(int arr[], int len)),支持任意长度的 int 数组排序,提高代码复用性。
五、总结
希尔排序是一种 "性价比很高" 的排序算法:
- 实现简单,仅需在直接插入排序的基础上增加增量控制;
- 效率优于直接插入排序、冒泡排序等基础排序算法,适合中等规模数据排序;
- 原地排序,空间开销小,在内存有限的场景下优势明显。
如果你需要进一步优化代码(如实现 Hibbard 增量序列),或想了解希尔排序与快速排序、归并排序的性能对比,欢迎补充需求,我们可以继续深入探讨!