leetcode 2654

2654: 使数组所有元素变成1 的最少操作次数

首先，如果所有数的 GCD（最大公约数）大于 1，那么无论如何都无法操作出 1，我们返回 −1。如果 nums 中有一个 1，那么从 1 向左向右不断替换就能把所有数变成 1。

如果 nums 中没有 1，想办法花费尽量少的操作得出一个 1。由于只能操作相邻的数，所以这个 1 必然是一个连续子数组的 GCD。（如果在不连续的情况下得到了 1，那么这个 1 只能属于其中某个连续子数组，其余的操作是多余的。）那么找到最短的 GCD 为 1 的子数组，设其长度为 minSize，那么我们需要操作 minSize−1 次得到 1。例如 2,6,3,4 中的 3,4 可以操作 2−1=1 次得到 1。

然后就转化成提示 1 中的情况了，最终答案为(minSize−1)+(n−1)=minSize+n−2

gcd_all=gcd(gcd_all,x);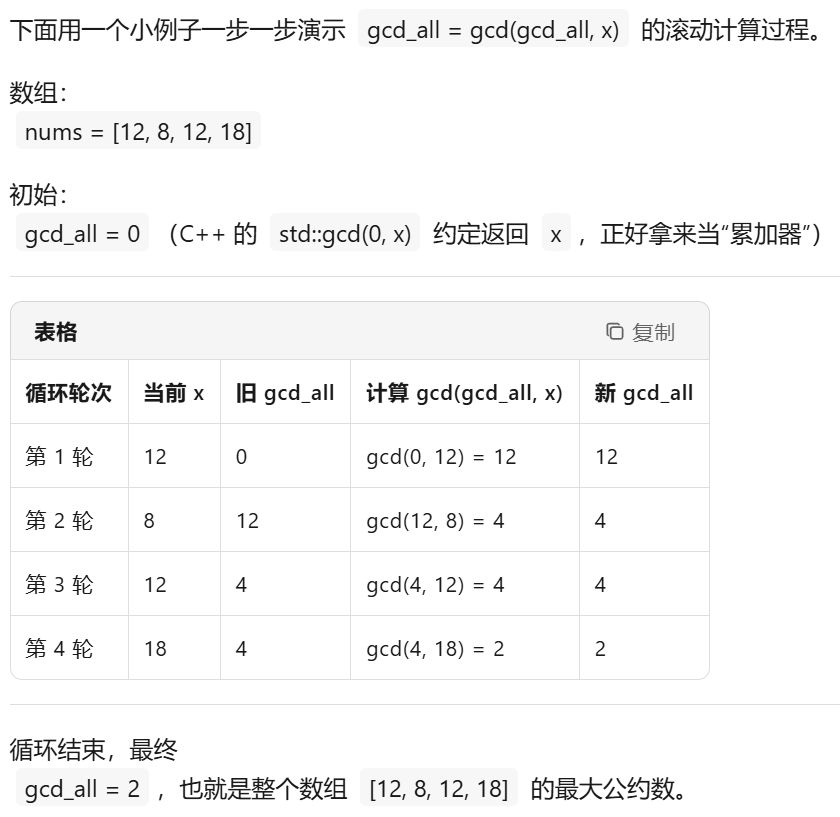

数学上规定：gcd(0, x) = |x| （任何整数与 0 的最大公约数都是它自身的绝对值）

class Solution {
public:
    int minOperations(vector<int>& nums) {
        int n=nums.size();
        int gcd_all=0,cnt1=0; //数学上规定：gcd(0, x) = |x|
        for(int x :nums){
            gcd_all=gcd(gcd_all,x);
            if(x==1) cnt1++;
        }
        if(gcd_all>1) return -1;
        //如果 nums 中存在 1
        if(cnt1) return n-cnt1;

        int minSize=n;
        for(int i=0;i<n;i++){  //找最短的 GCD 为 1 的子数组
            int g=0;
            for(int j=i;j<n;j++){
                g=gcd(g,nums[j]);
                if(g==1){
                    minSize=min(minSize,j-i+1); //需要操作 minSize−1 次得到 1
                    break;
                }
            }
        }

        return minSize+n-2;
    }
};