栈
- 电脑中的存储体系
- CPU的访问
- 深入理解栈:从概念到实现的完整指南
-
- 一、栈是什么?核心特性是什么?
- 二、栈的两种实现方式
-
- [方式 1:顺序栈(数组实现)](#方式 1:顺序栈(数组实现))
-
- [1. 结构定义](#1. 结构定义)
- 2.核心操作实现
-
- [(1) 初始化栈](#(1) 初始化栈)
- [(2) 销毁栈](#(2) 销毁栈)
- [(3) 入栈(Push)](#(3) 入栈(Push))
- [(4) 出栈(Pop)](#(4) 出栈(Pop))
- [(5) 取栈顶元素与判空](#(5) 取栈顶元素与判空)
- [(6) 栈数据个数](#(6) 栈数据个数)
- [方式 2:链式栈(链表实现)](#方式 2:链式栈(链表实现))
-
- [1. 结构定义](#1. 结构定义)
- [2. 核心操作实现](#2. 核心操作实现)
- [三、顺序栈 vs 链式栈:如何选择?](#三、顺序栈 vs 链式栈:如何选择?)
- 四、栈的经典应用场景
- 五、栈的测试代码
- 六、总结
电脑中的存储体系
电脑中常见的就只有两种存储体系:内存和硬盘。
其他配置中也可分为寄存器(CPU)、高速缓存(分为多种)、远程二级存储(网盘)。
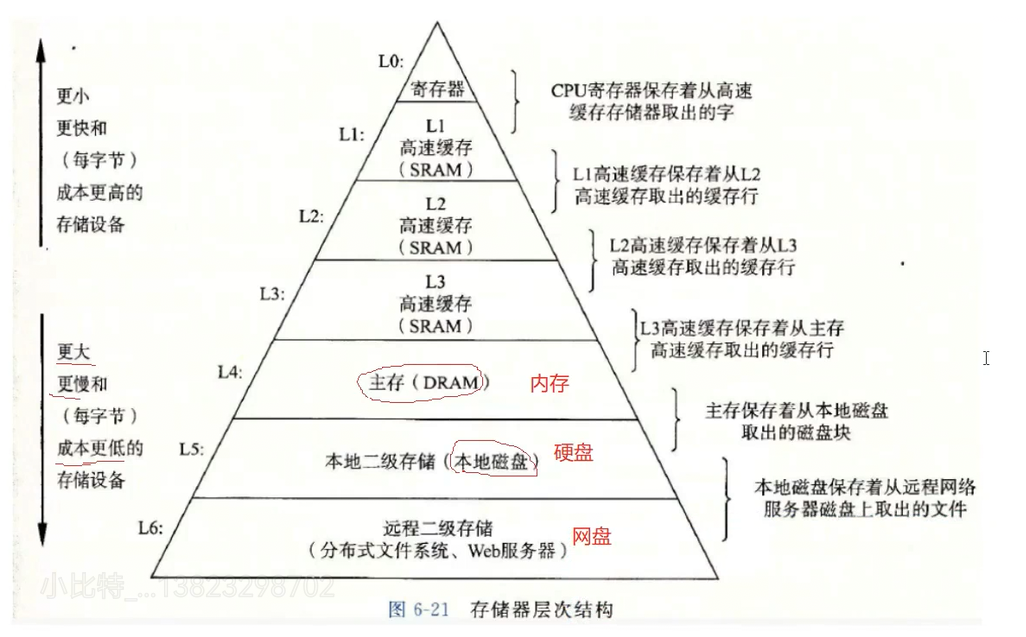
- 内存为带电存储,当电脑断电时,内容就会消失
- 硬盘把内容保存在磁盘上时,即使关机保存的内容也不会消失
列如:在编写代码时,创建的变量所申请的空间就是在内存上申请,当结束编译时内存会被释放
CPU的访问
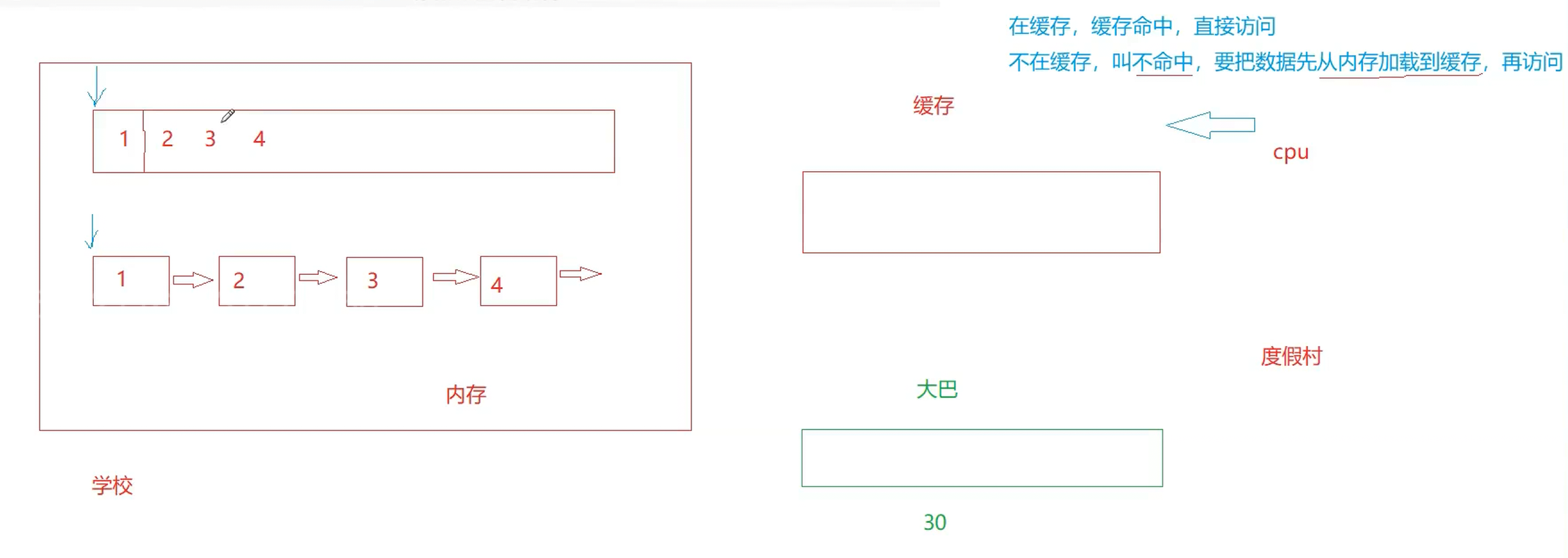
CPU的运行速度很快,通常会执行+、-、等其他指令。但由于速度太快,不会直接访问内存(内存的运行速度相对于CPU慢很多)。
假设创建了顺序表和链表,两个表会在内存中进行存储。由于CPU不会直接访问内存,会产生两种访问方式:
若顺序表和链表存在缓存中,CPU会直接进行访问
若顺序表和链表不存在缓存中,会把内存中的数据加载到缓存中,再由CPU进行访问
比如一个学校--->内存,校车--->缓存,度假村--->CPU。校车需要把学校里的学生送去度假村,需要用校车接送,此时缓存中有了数据,CPU就可以访问缓存里的数据了。对顺序表类似于:校车有30个空位,老师点名了接送1号学生过去。因为校车还有很多多余的位置,司机(缓存)就会将排了序的同学一起接走,从而达到效率最高
对链表:链表可能会造成缓存污染,是由于链表会指向其他不需要的数据,而有用的数据没进到缓存中,CPU访问了无用数据
深入理解栈:从概念到实现的完整指南
栈(Stack)是计算机科学中最基础也最常用的数据结构之一,它的 "后进先出" 特性在很多场景中都能发挥关键作用。本文将带你从核心概念 到代码实现,全面掌握栈的原理与应用。
一、栈是什么?核心特性是什么?
如果用生活中的例子类比,栈就像一摞叠起来的盘子:
- 要放新盘子,只能放在最上面(最后放的盘子在最顶端)。
- 要拿盘子,只能从最上面拿(最先拿到的是最后放的盘子)。
这种特性被称为 "后进先出"------ 最后进入栈的元素,最先被弹出。
栈的关键术语:
- 栈顶(Top):栈中最顶端的元素(最后加入的元素)。
- 栈底(Bottom):栈中最底端的元素(最先加入的元素)。
- 入栈(Push):向栈中添加元素(只能从栈顶添加)。
- 出栈(Pop):从栈中移除元素(只能从栈顶移除)。
- 判空(IsEmpty):判断栈中是否有元素。
- 取栈顶元素(GetTop):获取栈顶元素的值(不删除)。
二、栈的两种实现方式
栈的实现有两种经典方式:顺序栈 (用数组实现)和链式栈(用链表实现)。两种方式各有优劣,我们分别来看。
方式 1:顺序栈(数组实现)
顺序栈用数组存储元素,通过一个 "栈顶指针" 记录当前栈顶位置,操作效率高(时间复杂度 O (1))
1. 结构定义
C
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef int STDataType;
typedef struct Stack
{
STDataType* a;// 存储元素的数组
int top; // 栈顶指针(指向栈顶元素的下标)
int capacity; // 栈的最大容量(支持动态扩容)
}ST;2.核心操作实现
(1) 初始化栈
C
void STInit(ST* pst);
C
//初始化和销毁
void STInit(ST* pst)
{
assert(pst);
pst->a = NULL;
// top指向栈顶数据下一个位置
pst->top = 0;
// top指向栈顶数据
//pst->top = -1;
pst->capacity = 0;
}(2) 销毁栈
C
void STDestroy(ST* pst);
C
void STDestroy(ST* pst)
{
assert(pst);
free(pst->a);
pst->a = NULL;
pst->top = pst->capacity = 0;
}(3) 入栈(Push)
C
void STPush(ST* pst, STDataType x);
C
//入栈 出栈
void STPush(ST* pst, STDataType x)
{
assert(pst);
// 动态扩容(辅助函数)
if (pst->top == pst->capacity)
{
int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDataType* tmp = (STDataType*)realloc(pst->a, newcapacity * sizeof(STDataType));
if (tmp == NULL)
{
perror("realloc");
return;
}
pst->a = tmp;
pst->capacity = newcapacity;
}
// 因为top = 0,指向的是栈顶的元素,不需要像top = -1那样加1
pst->a[pst->top] = x;
pst->top++;
}(4) 出栈(Pop)
C
void STPop(ST* pst);
C
void STPop(ST* pst)
{
assert(pst);
assert(pst->top > 0);// 栈空,无法出栈
pst->top--;// 栈顶指针下移(逻辑删除,无需真正清除数据)
}(5) 取栈顶元素与判空
C
//判空
bool STEmpty(ST* pst);
C
//获取栈顶的数据
STDataType STTop(ST* pst)
{
return pst->a[pst->top - 1];
}
//判空
bool STEmpty(ST* pst)
{
assert(pst);
return pst->top == 0;
}test文件中判空的使用:遍历栈的元素
C
while (!STEmpty(&s))
{
//取栈顶
printf("&d ", STTop(&s));
//删一个元素
STPop(&s);
}(6) 栈数据个数
C
//取数据个数
int STSize(ST* pst);
C
//获取数据个数
int STSize(ST* pst)
{
assert(pst);
//因为top指向栈顶下一个元素
return pst->top;
}方式 2:链式栈(链表实现)
链式栈用单链表存储元素,头节点作为栈顶(因为链表头插、头删效率最高,符合栈的操作特性)。
1. 结构定义
c
// 链式栈节点结构
typedef struct StackNode {
StackDataType data; // 数据域
struct StackNode* next; // 指针域(指向下一个节点)
} StackNode;
// 链式栈管理结构(可选,方便记录栈顶和长度)
typedef struct {
StackNode* top; // 栈顶指针(指向头节点)
int size; // 栈中元素个数
} LinkStack;2. 核心操作实现
(1)初始化栈
c
// 初始化链式栈
void LinkStackInit(LinkStack* lst) {
lst->top = NULL; // 栈顶初始化为空(空栈)
lst->size = 0;
}(2)入栈(Push)
c
// 创建新节点(辅助函数)
StackNode* CreateNode(StackDataType val) {
StackNode* node = (StackNode*)malloc(sizeof(StackNode));
if (node == NULL) {
perror("malloc failed");
exit(1);
}
node->data = val;
node->next = NULL;
return node;
}
// 入栈:在链表头部添加节点(栈顶)
void LinkStackPush(LinkStack* lst, StackDataType val) {
StackNode* newNode = CreateNode(val);
newNode->next = lst->top; // 新节点指向原栈顶
lst->top = newNode; // 栈顶更新为新节点
lst->size++;
}(3)出栈(Pop)
c
// 出栈:删除链表头部节点(栈顶)
void LinkStackPop(LinkStack* lst) {
if (lst->top == NULL) { // 栈空
printf("栈为空,无法出栈\n");
return;
}
StackNode* delNode = lst->top; // 记录要删除的节点
lst->top = lst->top->next; // 栈顶指针后移
free(delNode); // 释放内存
lst->size--;
}(4)取栈顶元素与判空
c
// 取栈顶元素
StackDataType LinkStackTop(LinkStack* lst) {
if (lst->top == NULL) {
printf("栈为空,无元素可取\n");
exit(1);
}
return lst->top->data;
}
// 判断栈是否为空
bool LinkStackEmpty(LinkStack* lst) {
return lst->top == NULL; // 栈顶为空时栈空
}(5)销毁栈
c
// 销毁链式栈
void LinkStackDestroy(LinkStack* lst) {
StackNode* cur = lst->top;
while (cur != NULL) {
StackNode* next = cur->next;
free(cur);
cur = next;
}
lst->top = NULL;
lst->size = 0;
}三、顺序栈 vs 链式栈:如何选择?
| 特性 | 顺序栈(数组) | 链式栈(链表) |
|---|---|---|
| 内存分配 | 连续内存,可能需要动态扩容 | 非连续内存,按需分配节点 |
| 操作效率 | 入栈 / 出栈效率高(O (1)) | 入栈 / 出栈效率高(O (1)) |
| 空间利用率 | 可能有内存浪费(扩容后未用空间) | 无浪费(节点数量等于元素数量) |
| 实现复杂度 | 较简单(依赖数组下标) | 稍复杂(需处理指针) |
选择建议:
- 若元素数量固定或可预估,优先用顺序栈(实现简单,缓存友好)。
- 若元素数量动态变化大,优先用链式栈(空间利用率高,无需考虑扩容)。
四、栈的经典应用场景
栈的 "后进先出" 特性使其在很多场景中不可或缺:
- 函数调用栈
程序运行时,函数调用通过栈管理:每次调用函数时,将函数的参数、返回地址等压入栈;函数执行结束后,从栈顶弹出这些信息,回到调用位置。这也是递归函数的实现基础。 - 表达式求值
计算数学表达式(如(1+2)*(3-4))时,栈可用于处理运算符的优先级和括号匹配。 - 括号匹配
遍历字符串时,遇到左括号((/{/[)则压栈,遇到右括号则弹出栈顶元素检查是否匹配,最终栈为空则匹配成功。 - 浏览器历史记录
浏览器的 "后退" 功能本质是一个栈:每次访问新页面时压栈,点击 "后退" 时出栈并显示前一个页面。
五、栈的测试代码
以下是顺序栈的测试示例(链式栈类似):
c
// 测试顺序栈
void TestStack() {
Stack st;
StackInit(&st);
// 入栈测试
StackPush(&st, 1);
StackPush(&st, 2);
StackPush(&st, 3);
printf("栈顶元素:%d\n", StackTop(&st)); // 输出:3
// 出栈测试
StackPop(&st);
printf("出栈后栈顶:%d\n", StackTop(&st)); // 输出:2
// 判空测试
printf("栈是否为空:%s\n", StackEmpty(&st) ? "是" : "否"); // 输出:否
// 销毁栈
StackDestroy(&st);
}
int main() {
TestStack();
return 0;
}六、总结
栈是一种遵循 "后进先出" 规则的线性数据结构,核心操作包括入栈、出栈、取栈顶元素和判空。它可以通过数组(顺序栈)或链表(链式栈)实现,各有适用场景。
理解栈的关键是抓住 "只能在栈顶操作" 这一特性,这使得它在函数调用、表达式求值、括号匹配等场景中成为不可替代的工具。掌握栈的实现后,你可以尝试用它解决更多实际问题,比如实现一个简单的计算器或括号匹配检测器