数据结构-堆 - 技术栈

优先级队列

队列是一个先进先出 的数据结构，但有些情况下，操作的数据可能带有优先级 ，一般出队列时，可能需要优先级高的元素先出队列 。所以这个数据结构应该提供两个最基本的操作，一个是返回最高优先级对象 ，一个是添加新对象 。这种数据结构就是优先级队列

想要实现优先级队列，就要知道堆的概念

堆

如果一个关键码的集合K={k0,k1,k2,...,kn-1}，把它所有的元素按照完全二叉树 的方式存储在一维数组中，并满足ki<=k2i+1且ki<=k2i+2(ki >= k2i+1 且 ki >= k2i+2)（说人话就是父亲比孩子小或者父亲比孩子大 ），则称为小堆（大堆） 。将根节点最大 的堆称为大堆或者大根堆 ，根节点最小 的堆称为最小堆或者小根堆。

堆的性质

**1.**堆中某个节点的值总是不大于或者不小于其父节点的值

2. 堆总是一颗完全二叉树

堆的储存方式

堆是一颗完全二叉树 ，因此可以层序遍历的规则来顺序存储

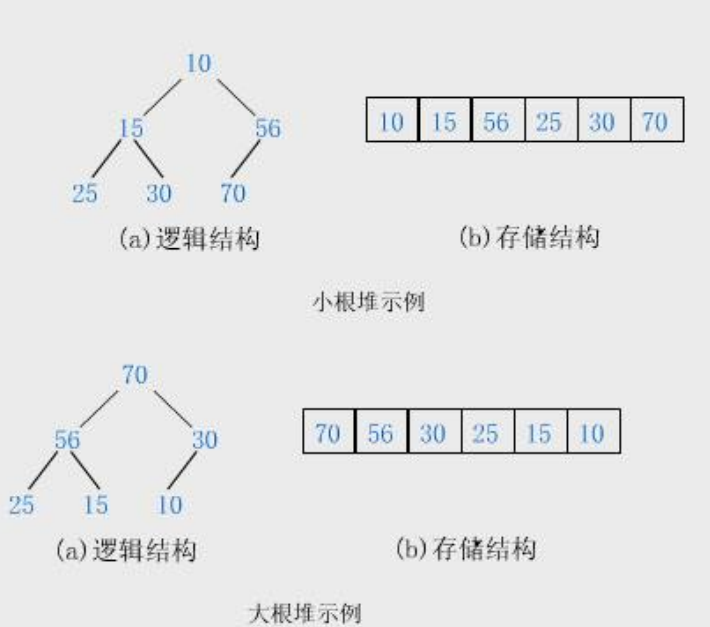
元素存储到数组之后按照如下性质进行还原

如果i为0，则i表示的节点为根节点，否则i的父亲节点为**(i-1)/2** ，同理已知父节点为i，子节点 为2*i+1，2*i+2。

堆的创建

堆的向下调整（以大堆为例）

如果parent的左孩子存在则进行如下操作，直到左孩子不存在

从上往下调整 ：将倒数第二层的节点作为根节点 ，如果右孩子存在 ，则取两个孩子之间的较大值 与父节点进行比较，如果大于 则进行交换。并将交换顺序的孩子 作为根节点，继续重复进行，直到左孩子为空。之后parent--，重复进行

代码：

java 复制代码

public static void creatHeap(){
        int len=this.usedsize;
        int parent=(len-1-1)/2;
        for(int i=parent;i>=0;i--){
                shiftDown(i,i*2+1,len);
        }
   }
public void shiftDown(int parent,int child，int len){
        while(child<len){
            if(child+1<len && this.array[child]<this.array[child+1]){
                child++;
            }
            if(this.array[child]>this.array[parent]){
                int tmp=this.array[parent];
                this.array[parent]=this.array[child];
                this.array[child]=tmp;
                parent=child;
                child=child*2+1;
            }else{
                break;
            }
        }
    }

此时建堆的时间复杂度为O(N)

堆的插入

1.进行容量判断 2.将新的节点插入最后然后向上调整

java 复制代码

 private void shiftUp(int child){
        int root=(child-1)>>1;
        while(root>=0){
            if(array[child]>array[root]){
                int tmp=array[root];
                array[root]=array[child];
                array[child]=tmp;
                child=root;
                root=(child-1)>>1;
            }else{
               break;
            }
        }
    }
    public void push(int x){
        int len=array.length;
            if(this.usedsize==len){
                array= Arrays.copyOf(array,2*len);
            }
            array[this.usedsize]=x;
        shiftUp(this.usedsize);
        this.usedsize++;
    }

进行一次向上调整的时间复杂度为**（logn)** ，如果是通过向上调整来逐个创建堆那么时间复杂度就是O(n*logn)

堆的删除

1.将堆顶元素与堆中最后一个元素交换 2.usedsize-- 3.对堆顶元素进行向下调整

java 复制代码

    public int poll(){
        int tmp=this.array[0];
        this.array[0]=this.array[this.usedsize-1];
        this.array[this.usedsize-1]=tmp;
        shiftDown(0,usedsize-1);
        usedsize--;
        return tmp;
    }

堆的应用

进行堆排序

1.升序：建大堆 降序：建小堆

2.然后利用堆的删除思想，进行排序

java 复制代码

    public void heapSort(){
        int len=this.usedsize;
        for(int i=len-1;i>0;i--){
            int tmp=array[i];
            array[i]=array[0];
            array[0]=tmp;
            shiftDown(0,i-1);
        }
    }

Top-k问题

N个数据 ，找前k个最大的或者第k大或者第k小的数据。一般N很大，k很小

对于Top-k问题，能想到的最简单最直接的办法就是排序，但是如果数据量非常大，排序就不太可取了。最佳的方式就是通过堆来解决

一用数据集合中前k 的元素来建堆

1.前k个最大的元素，则建小堆

2.前k个最小的元素，则建大堆

二用剩余N-k个元素依次与堆顶元素比完之后，堆中剩余的k个元素就是所求的k个最小或者最大的元素

java 复制代码

class cmp implements Comparator<Integer>{
    public int compare(Integer o1,Integer o2){
        return o2.compareTo(o1);
    }
}
class Solution {
    public int[] smallestK(int[] arr, int k) {
        int[] array=new int[k];
        if(arr.length==0||k==0) return array;
        PriorityQueue<Integer> queue=new PriorityQueue(k,new cmp());
        for(int i=0;i<k;i++){
            queue.offer(arr[i]);
        }
        for(int i=k;i<arr.length;i++){
            if(arr[i]<queue.peek()){
                queue.poll();
                queue.offer(arr[i]);
            }
        }
        for(int i=0;i<k;i++){
            array[i]=queue.poll();
        }
        return array;
    }
}

时间复杂度为NlogK

优先级队列

PriorityQueue的特性

Java集合框架中提供了PriorityQueue 和PriorityBlockingQueue 两种优先级队列，PriorityQueue是线程不安全的 ，PriorityBlockingQueue是线程安全的。

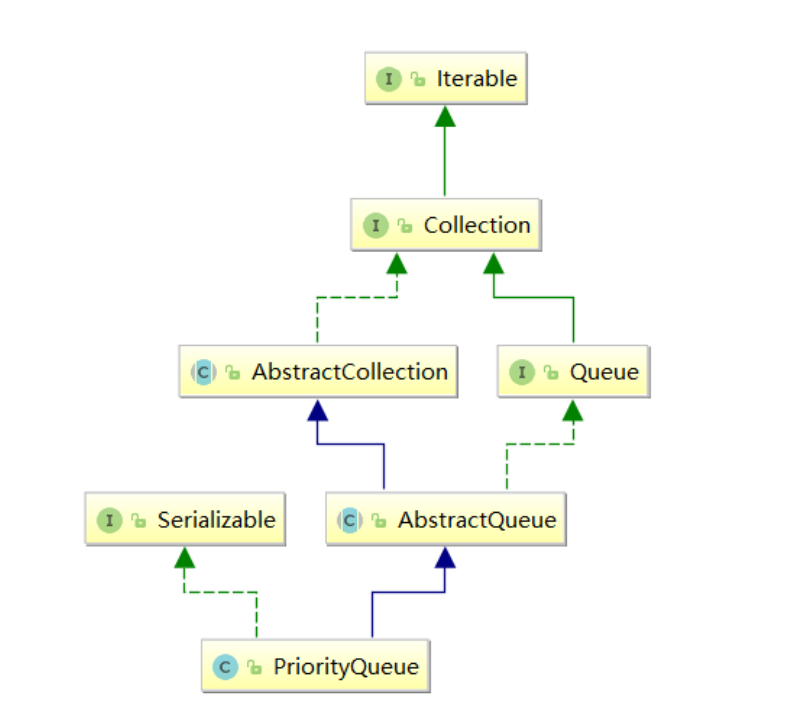
注意：

1.使用时导入包

java 复制代码

import java.util.PriorityQueue;

2. PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出异常

3.不能插入null对象

4.没有容量限制，可以插入任意多个元素，其内部可以自动扩容

5. 插入和删除元素的时间复杂度为O(logN)

6 .PriorityQueue底层使用了堆数据结构

7. PriorityQueue默认情况下是小堆

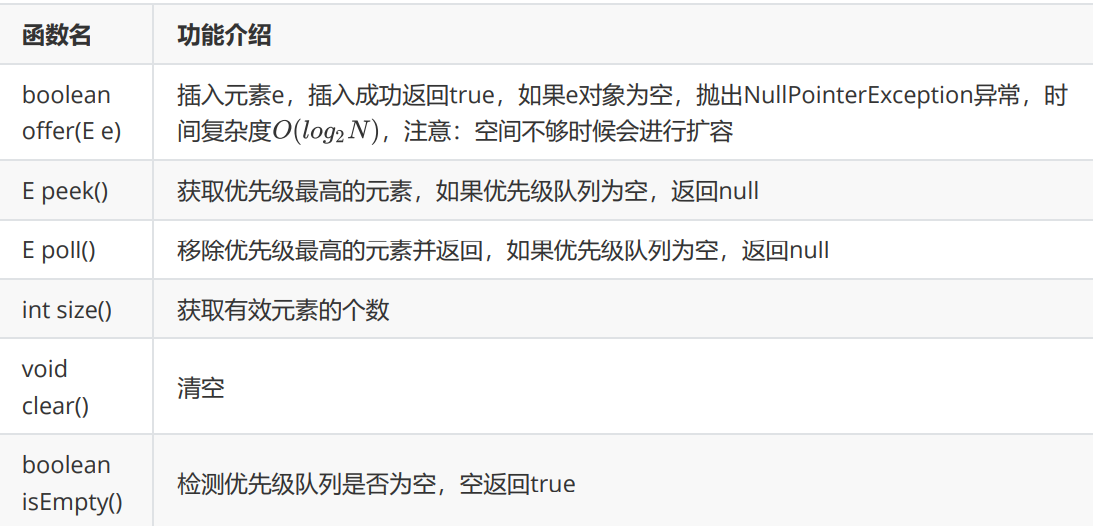
常用接口介绍

1.优先级队列的构造方法

源码：

java 复制代码

        PriorityQueue<Integer> p1 = new PriorityQueue<>();
        p1.offer(6);
        p1.offer(5);
        p1.offer(9);
        PriorityQueue<Integer> p2=new PriorityQueue<>(p1);

默认条件下，队列是小堆，如果需要大堆需要用户自己提供比较器

java 复制代码

class sort implements Comparator<Integer>{
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2-o1;
    }
}
        PriorityQueue<Integer> p1 = new PriorityQueue<>(5,new sort());
        p1.offer(6);
        p1.offer(5);
        p1.offer(9);
        PriorityQueue<Integer> p2=new PriorityQueue<>(p1);

第二个构造方法会继承p1的接口

扩容机制

如果容量小于64时 ，两倍扩容 ，大于等于64 时，按照1.5倍扩容 。如果超过了整数的最大值，那么按照整数的最大值进行扩容

Java中数据的比较

equals

在Java中所有的数据类型（包括用户实现的自定义类型）都默认继承自Object类，而Object类提供了equal方法，而==默认情况下就是调用equal方法。比较规则是基本类型比较内容，引用类型比较地址 ，如果想比较引用变量的内容，就需要重写equals方法

java 复制代码

    public boolean equals(Object obj) {
        if(this==obj) return true;
        if(!(obj instanceof Student)) return false;
        Student c= (Student)obj;
        if(c.age==this.age&&c.name.equals(this.name)) return true;
        return false;
    }

Comparable接口

java 复制代码

   class Student implements Comparable<Student> 
@Override
   public int compareTo(Object o) {
        Student s=(Student) o;
        return this.age-s.age;
    }
  //两者留一个
    @Override
    public int compareTo(Object o) {
        Student s=(Student) o;
        return s.name.compareTo(this.name);
    }

因为String类 中已经重写了equals和compareTo方法，可以直接调用

缺点：一旦需要更改比较方式 ，就需要更改源代码，并不方便

自定义比较器

java 复制代码

class AgeComparator implements Comparator<Student> {
    @Override
    public int compare(Student o1, Student o2) {
        return o1.age-o2.age;
    }
}
class NameComparator implements Comparator<Student>{
    @Override
    public int compare(Student o1, Student o2) {
        return o1.name.compareTo(o2.name);
    }
}

使用时需要导入包