本文较长,建议点赞收藏。更多AI大模型应用开发学习视频及资料,在智泊AI。
在AI的世界里万物皆向量,向量可以用统一的方式表示一切信息:图片-像素,文字-编码,声音-频率特征向量,文件-向量化。前文介绍了线性代数:标量、向量、矩阵、张量;矩阵乘法、转置、点积运算等基本知识。深度学习的本质就是数学运算,而向量和矩阵是基石。神经网络的前向传播、反向传播、梯度下降,都离不开向量和矩阵运算。
本文重点介绍点积计算如何应用在transformer注意力机制中。你肯定好奇到底点积运算发挥了什么作用,这篇文章篇幅较长,比较烧脑,纰漏之处欢迎指出讨论,本文重点结合理论与代码实践回答下面几个问题。
1)什么是向量的点积运算?python如何实现点积运算?
2)点积运算与向量相似度有什么关系?python如何计算相似度?
3)相似度与transformer里面注意力attention机制又是什么关系?
4)python实现注意力机制。
1.什么是点积运算?
点积是深度学习中最基础、最重要的运算,它是每个神经元进行计算的核心操作。点积(Dot Product)是两个向量之间的一种运算,结果是一个标量。用于衡量两个向量在方向上有多"一致"。两种定义:
1)代数定义: A · B = a1b1 + a2b2 + ... + an*bn,对应位置的分量相乘,然后将所有乘积结果相加。神经网络的"智能"就来自于学会给不同输入分配合适的权重,然后做加权求和。向量点积运算就是这个加权求和过程,让每个输入乘以权重,全部加起来。不同神经元的点积运算重复千万次,就产生了人工智能(大道至简,从简单规则到复杂智能,是不是有点类似蚂蚁群体,单个蚂蚁类似神经元的能力极其有限,但当它们通过简单规则相互连接并大规模组织起来时,就会"涌现"出全新的、更高层次的特性)。
python
1.数学表达:
# 输入向量(比如一张简化的3像素图片)
input_vector =[1.0,0.5,2.0]
# 权重向量(神经元学到的参数)
weight_vector =[0.3,0.7,-0.1]
# 点积计算(这就是神经元在做的事情!)
result=1.0×0.3+0.5×0.7+2.0×(-0.1)=0.3+0.35-0.2=0.45
2.程序实现:利用python的numpy模块实现点积运算
# 输入向量(比如一张简化的3像素图片)
input_vector = np.array([1.0,0.5,2.0])
# 权重向量(神经元学到的参数)
weight_vector = np.array([0.3,0.7,-0.1])
# 点积计算(这就是神经元在做的事情!)
result = np.dot(input_vector,weight_vector)
print("点积计算结果:",result)
3.自己实现Vector向量类及点积运算函数
class Vector:
def __init__(self, components):
self.components = components
def dot(self, other):
if len(self.components)!=len(other.components):
raise ValueError("向量维度必须相同")
return sum(x * y for x, y in zip(self.components, other.components))2)几何定义: A · B = ||A|| * ||B|| * cos(θ),点积的结果由两个向量的长度和它们之间的夹角共同决定。
||A|| 是向量 A 的模长(可以理解为向量的长度)。
||B|| 是向量 B 的模长。
θ 是向量 A 和向量 B 之间的夹角。
3)模长||A||如何计算?向量的模长(Magnitude),也叫范数(Norm),直观来说就是向量在空间中的"长度",从原点(0,0,...)指向向量坐标点的距离。对于一个 n维向量 A = [a1, a2, a3, ..., an],其模长 ||A|| 的计算公式为:
||A|| = √(a1² + a2² + a3² + ... + an²)。
文字描述就是:向量模长等于其所有分量的平方和,再开平方根。假设有一个二维向量 A = [3, 4],它在坐标系中就是从原点 (0,0) 指向点 (3,4) 的箭头。计算分量的平方和: 3² + 4² = 9 + 16 = 25 对结果开平方根:√25 = 5,所以,向量 A 的模长 ||A|| = 5。
4)两种定义是等价的:点积的数学本质A · B = ||A|| * ||B|| * cos(θ),它同时衡量了向量的长度和方向一致性。
a1b1 + a2b2 + ... + an*bn = ||A|| * ||B|| * cos(θ)
让我们用一个二维的例子来可视化这个过程,这能极大地帮助理解。
假设有两个向量:A = [3, 4],B = [1, 0]
第一步:计算点积 A · B A · B = (3 * 1) + (4 * 0) = 3 + 0 = 3
第二步:计算模长 ||A|| 和 ||B|| ||A|| = sqrt(3² + 4²) = sqrt(9 + 16) = sqrt(25) = 5 ||B|| = sqrt(1² + 0²) = sqrt(1 + 0) = 1
第三步:计算余弦值 cos(θ) cos(θ) = (A · B) / (||A|| * ||B||) = 3 / (5 * 1) = 3/5 = 0.6
2.点积vs向量相似度是什么关系?
2.1向量相似度计算
如何衡量向量相似度?本质上,我们是用夹角余弦值 cos(θ) 来衡量"方向上的相似度",而点积 A · B 是计算 cos(θ) 的一个关键步骤,但它本身并不是一个纯粹的相似度度量。
1)最纯粹的相似度度量是 cos(θ):它只关心两个向量的方向是否一致,完全忽略了它们的长度(模长)。这使得它成为衡量"本质相似性"的理想指标。cos(θ) 的本质是衡量方向一致性:
✧ 当 θ = 0° 时,cos(0°) = 1。这意味着两个向量方向完全相同。此时点积达到最大值(正值)。
✧ 当 θ = 90° 时,cos(90°) = 0。这意味着两个向量互相垂直。此时点积为 0。
✧ 当 θ = 180° 时,cos(180°) = -1。这意味着两个向量方向完全相反。此时点积达到最小值(负值)。
所以,cos(θ) 本身就是一个完美的"相似度"度量指标,它衡量了两个向量在方向上的对齐程度。
2)点积 A · B 是 cos(θ) 的"未标准化"版本:点积的结果同时受到向量方向和向量长度的影响。 ||A|| * ||B|| 是缩放因子:它保证了更长的向量会对点积结果产生更大的影响。但如果两个向量的模长是固定的(归一化),那么点积的大小就完全由cos(θ),即方向的一致性来决定。
| 特征 | 点积 (Dot Product) | 余弦相似度 (Cosine Similarity) |
| 公式 | A · B = Σ(a_i * b_i) | cos(θ) = (A · B) / ( |
| 取值范围 | (-∞, +∞) | [-1, 1] |
| 受向量长度影响 | 是 | 否 |
| 衡量的是什么 | 方向相似性+强度(模长) | 纯方向相似性 |
| 主要用途 | 注高效计算相似度 | 理论上纯粹的相似度度量 |
2.2向量相似度实现
Transformer通过简单的点积运算(余弦相似度的核心)在大规模应用中"涌现"出强大的语言理解能力,这正是"大道至简"的完美体现。
python
import numpy as np
from numpy.linalg import norm
#基于numpy模块实现两个向量余弦相似度相似度计算
def cosine_similarity(vec1, vec2):
"""
计算两个向量的余弦相似度
公式:cos(θ)=(A·B)/(||A||*||B||)
值域:[-1,1],值越大表示越相似
1= 完全相同方向,0= 正交,-1= 完全相反方向
Args:
vec1 (list/np.array): 第一个向量
vec2 (list/np.array): 第二个向量
Returns:
float: 余弦相似度值
"""
# 确保输入是numpy数组
vec1 = np.array(vec1)
vec2 = np.array(vec2)
# 计算点积
dot_product = np.dot(vec1, vec2)
# 计算向量的模长(L2范数)
norm_vec1 =norm(vec1)
norm_vec2 =norm(vec2)
# 防止除以零
if norm_vec1 ==0 or norm_vec2 ==0:
return 0.0
# 计算余弦相似度
similarity = dot_product /(norm_vec1 * norm_vec2)
return similarity
# 纯Python实现(不依赖numpy),代数相似度vs几何相似度等价
def cosine_similarity_python(vec1, vec2):
"""不使用numpy的余弦相似度实现"""
# 计算点积
dot_product =sum(a * b for a, b in zip(vec1, vec2))
# 计算模长
norm1 =sum(a * a for a in vec1)**0.5
norm2 =sum(b * b for b in vec2)**0.5
# 防止除以零
if norm1 ==0 or norm2 ==0:
return 0.0
return dot_product /(norm1 * norm2)
#测试向量相似度
def test_cosine_similarity():
"""测试余弦相似度函数"""
print("===== 余弦相似度测试 =====")
# 相同方向的向量
a =[1,2,3]
b =[2,4,6] # a的2倍,完全同向
print(f"向量 {a} 和 {b} 的余弦相似度: {cosine_similarity(a, b):.4f} (应接近1.0)")
# 正交向量
c =[1,0,0]
d =[0,1,0]
print(f"向量 {c} 和 {d} 的余弦相似度: {cosine_similarity(c, d):.4f} (应为0.0)")
# 相反方向
e =[1,2,3]
f =[-1,-2,-3]
print(f"向量 {e} 和 {f} 的余弦相似度: {cosine_similarity(e, f):.4f} (应接近-1.0)")
# 实际应用示例 - 文本向量
# 假设是词嵌入向量
apple =[0.8,0.6,0.1,-0.2]
fruit =[0.7,0.5,0.2,-0.1]
car =[-0.1,-0.3,0.9,0.8]
print("\n实际应用示例 (词向量):")
print(f"apple 和 fruit 的相似度: {cosine_similarity(apple, fruit):.4f}")
print(f"apple 和 car 的相似度: {cosine_similarity(apple, car):.4f}")
print("=======================\n")
# 执行测试
test_cosine_similarity(3.向量相似度vs注意力机制什么关系?
3.1Transformer的自注意力机制
维基百科里面,注意力机制(英语:attention)是人工神经网络中一种模仿人类认知注意力的技术。这种机制可以增强神经网络输入数据中某些部分的权重,同时减弱其他部分的权重,以此将网络的关注点聚焦于数据中最重要的一小部分。数据中哪些部分比其他部分更重要取决于上下文。可以通过梯度下降法对注意力机制进行训练。允许模型在处理数据时动态分配权重,重点关注输入中的重要部分。让AI模型具备像人类一样"抓重点"的能力,这样AI在处理信息时也会自动分配"注意力权重",强化关键特征,弱化次要信息。
3.1.1transformer里面的self-attentionlayer
下面截图来自李宏毅老师的视频课程,这个结构相信大家看了无数遍。今天我们主要聚集这幅图里面的self-attentionlayer模块。
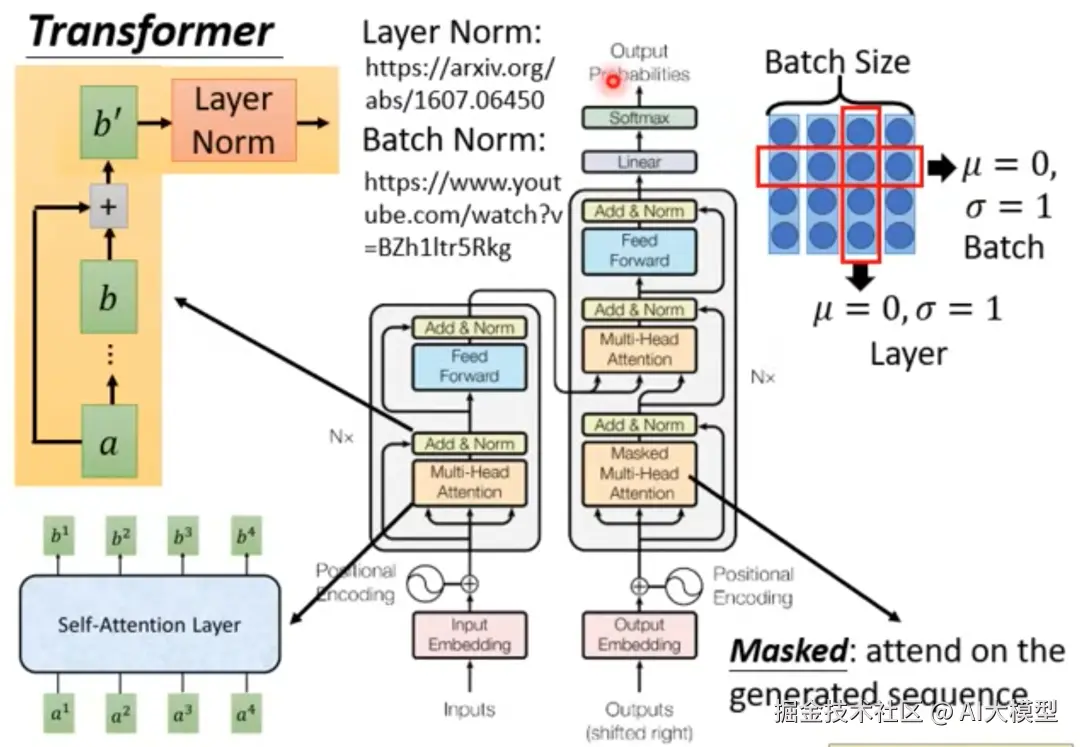
3.1.2Self-attention矩阵运算过程
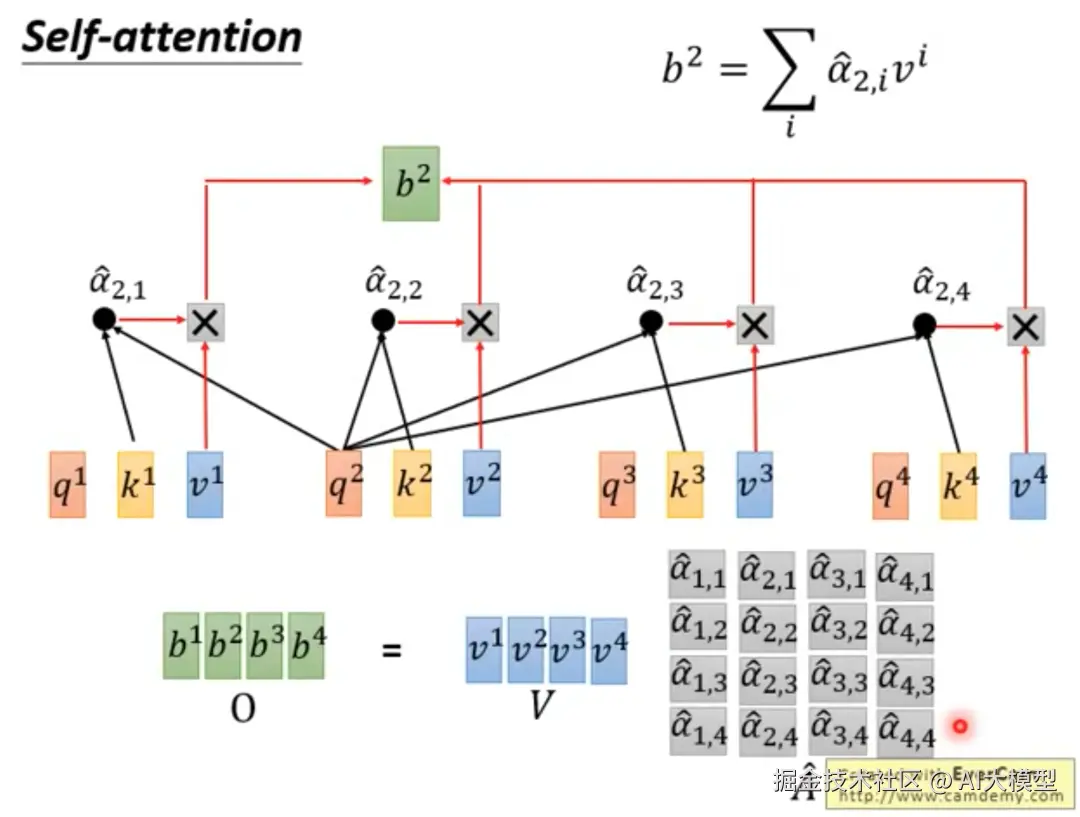
自注意力机制允许模型在处理序列数据时,关注输入序列中的不同部分。其核心是使用点积计算查询(Query)、键(Key)和值(Value)之间的相关性。自注意力机制公式:Attention(Q, K, V) = softmax(QKᵀ/√dₖ)V,点积用于计算查询(Query)和键(Key)之间的相似度。其中:Q: 查询矩阵,K: 键矩阵,V: 值矩阵,dₖ: 键向量的维度(用于缩放),整体步骤如下:
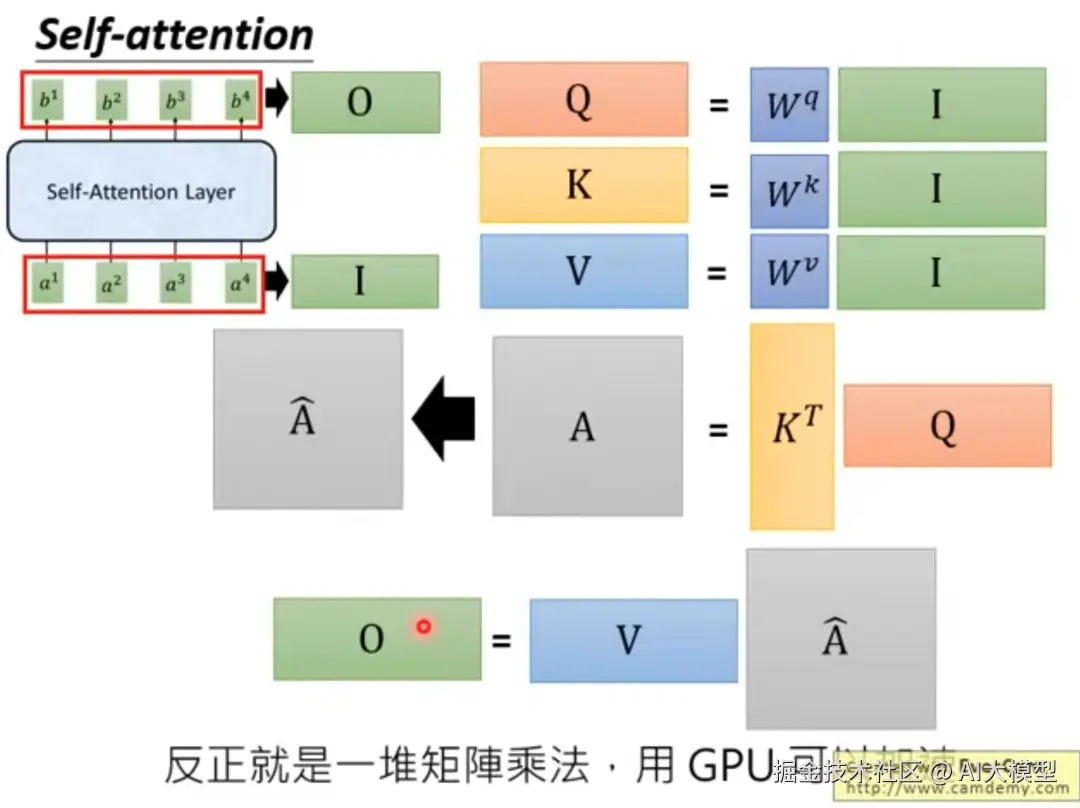
3.1.3运算步骤拆解
1)根据输入x与权重矩阵Wq,Wk,Wv计算Q、K、V矩阵。
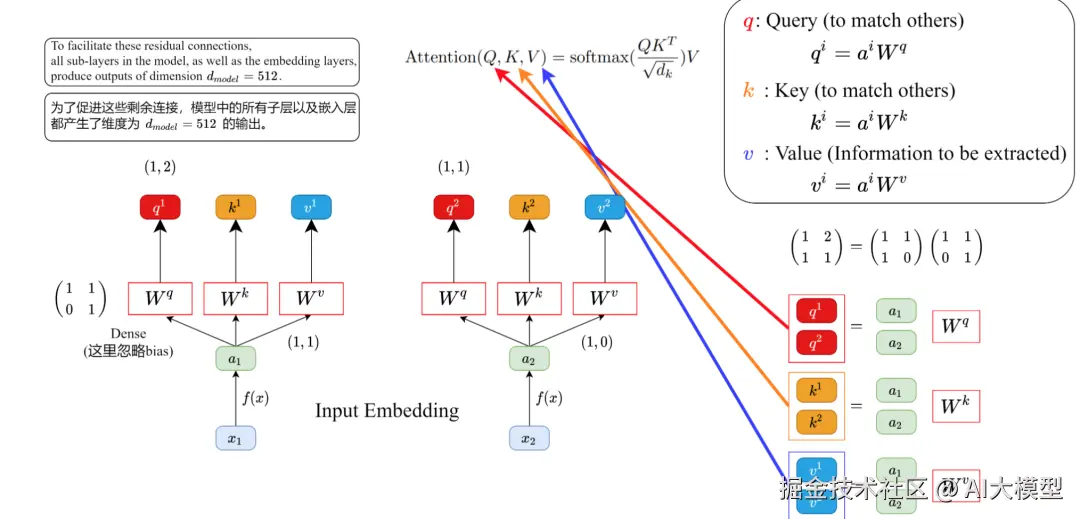
词向量xi+位置编码ei=ai------>WqWkWv*ai
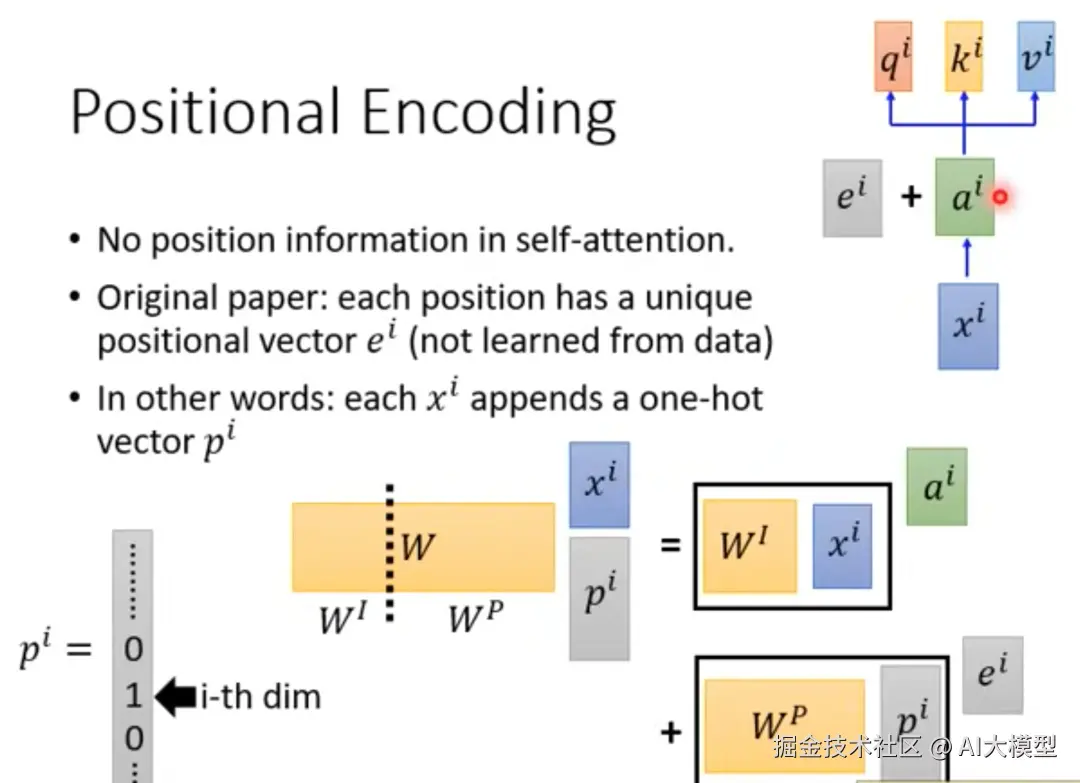
2)每个q与每个k做点积运算:Q*K做 dot product并行运算
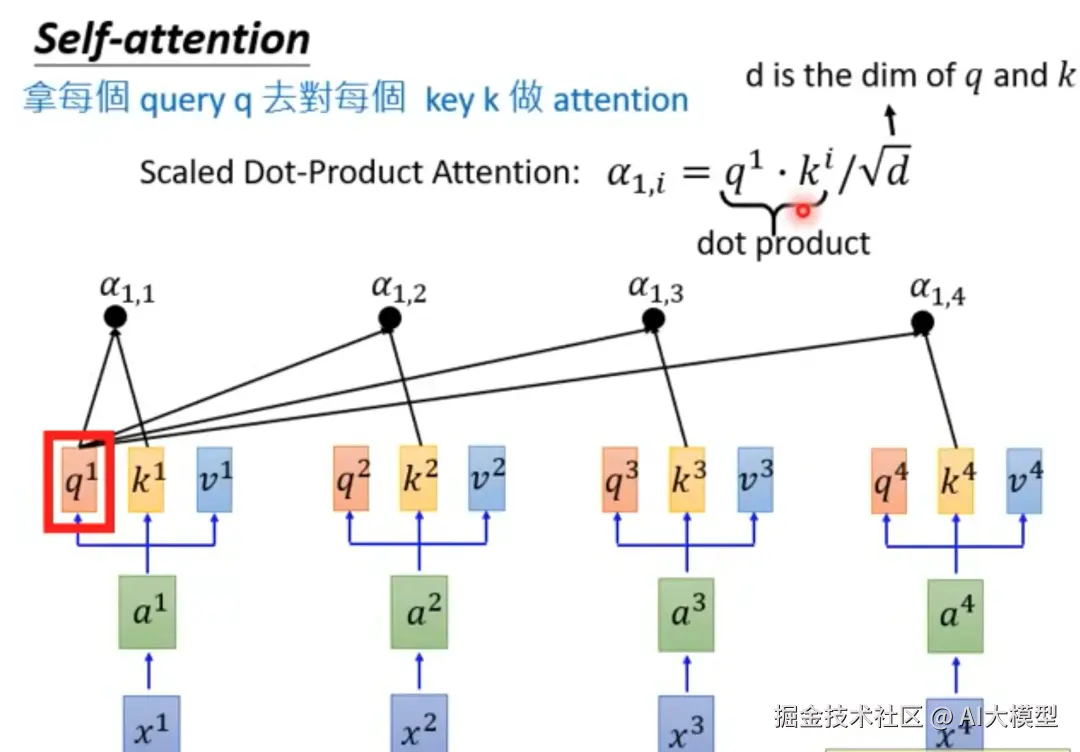
3)Softmax运算-归一化:矩阵运算结果进行softmax运算,将点积运算得到的原始分数转换为有意义的概率分布,是连接神经网络计算与概率解释的桥梁(这里不做展开,后面概率论单独文章再去理解)。
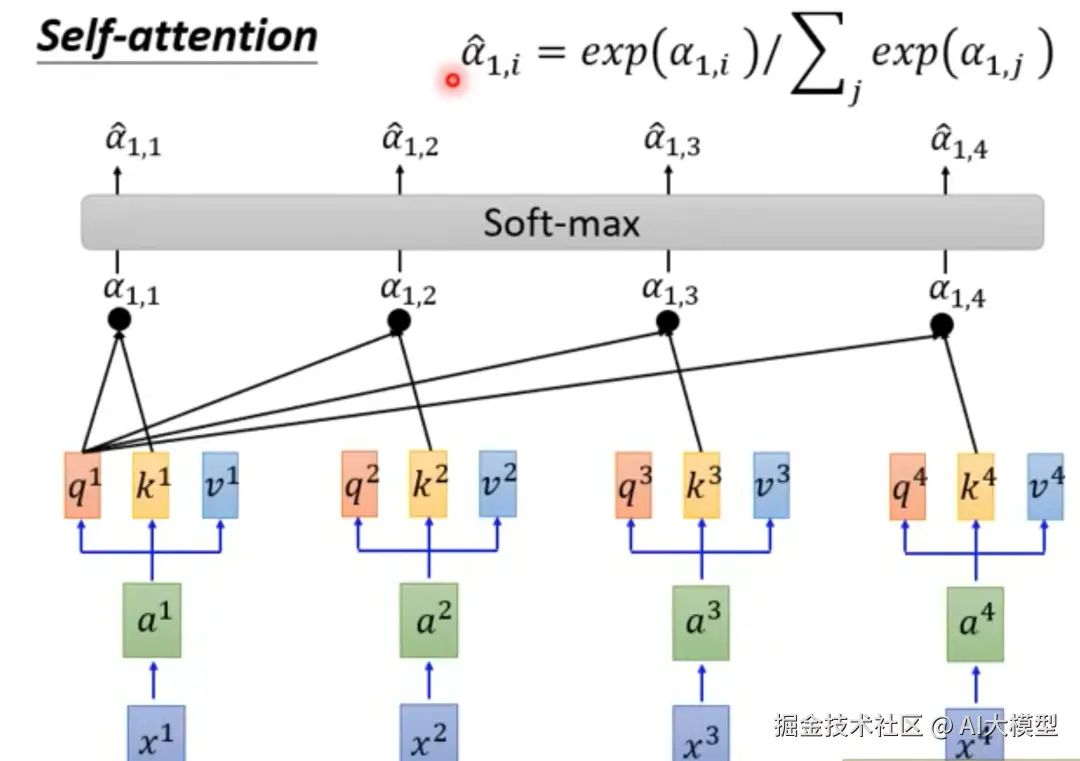
4)计算输出结果:
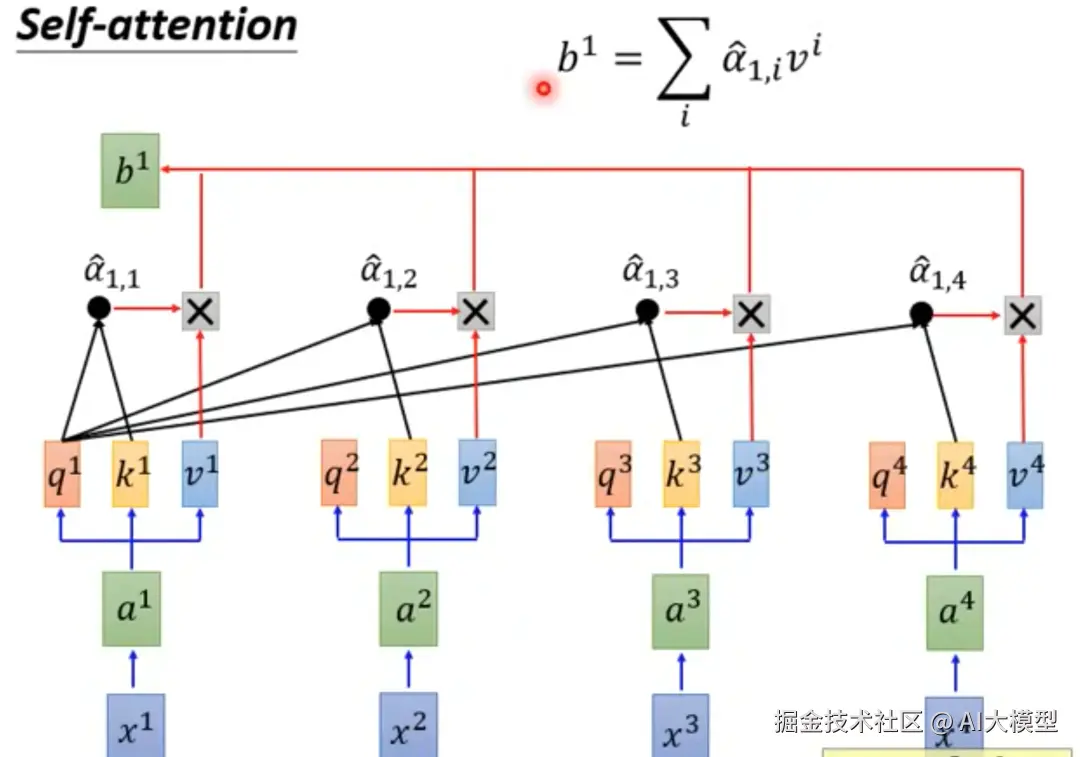
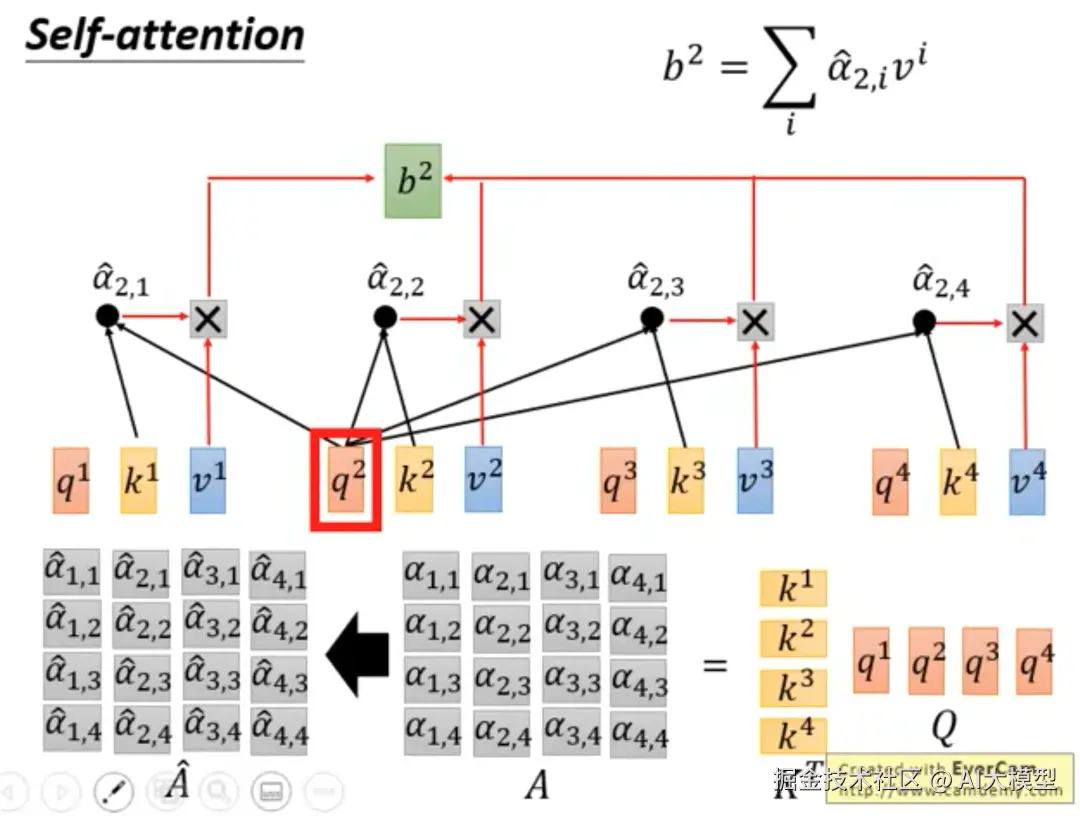
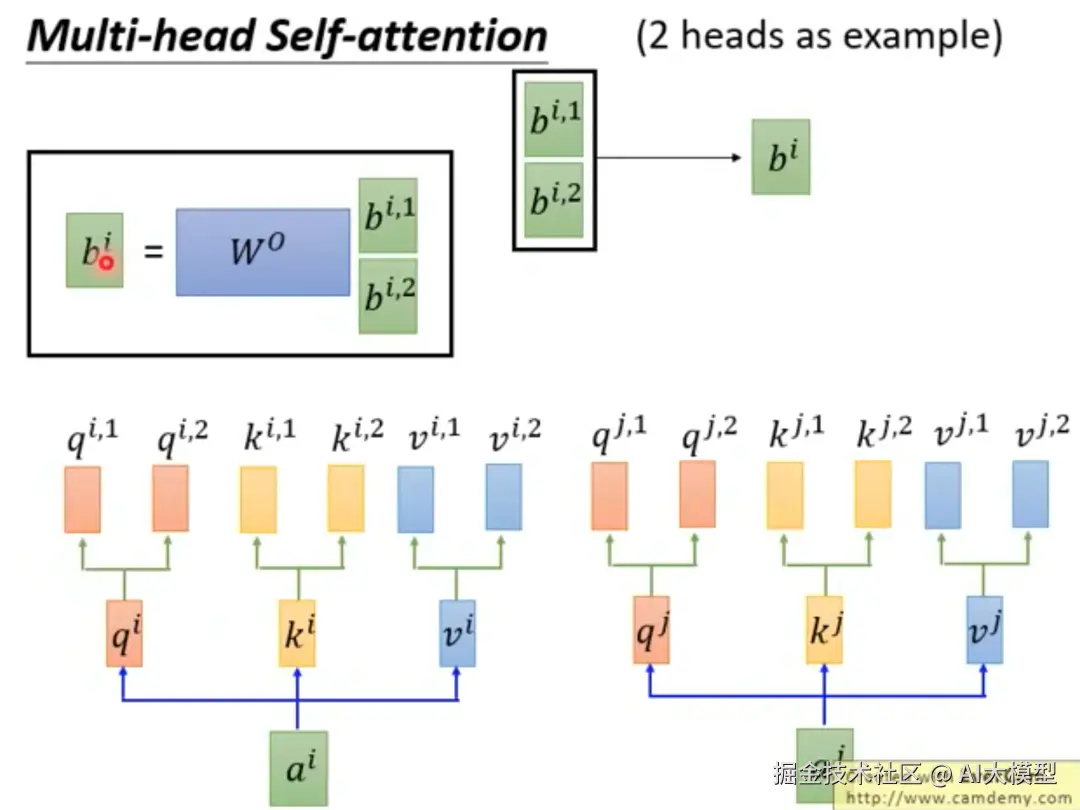
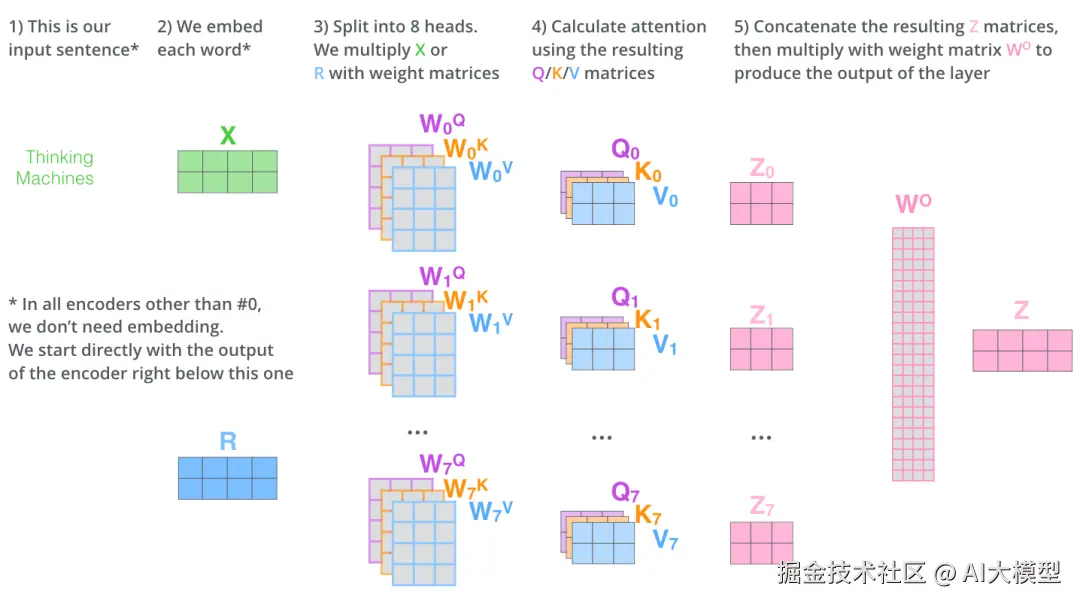
3.1.4多头自注意力机制:Q、K、V不同维度分解
多维度理解就像用多个不同角度的摄像头同时拍摄一个场景:
1)第一个头:专注语法关系(主谓宾结构)
2)第二个头:专注语义关系(词汇含义)
3)第三个头:专注长距离依赖(句子间逻辑)
3.2点积相似度计算vs注意力关系
点积在注意力中的角色:利用其衡量方向一致性的特性,来计算查询(Query) 和键(Key) 之间的相似度。方向越一致,代表Key越能回答Query的"提问",其对应的Value就越重要。
1)在概念上,我们是用 cos(θ) 来衡量向量的相似度。余弦的优势:余弦值通过除以模长,消除了向量长度的影响。cos(A, B) = 1 精确地表示它们方向完全相同。cos(A, C) = -1 表示它们方向完全相反。cos(θ) 给出了一个归一(Normalized)的结果,它的值永远在 [-1, 1] 之间,这使得不同向量之间的相似度可以公平地进行比较。
2)在实际操作中(尤其是在注意力机制里),我们常用点积 (Q · K) 作为其高效且有效的近似计算方式(例如,在Transformer中,Query和Key向量通常会被归一化到相同的尺度)。
3.3点积运算如何在transformer注意力机制中发挥作用?
Transformer原论文中将核心部分称为Scaled Dot-Product Attention,缩放点积注意力,最核心的公式为:
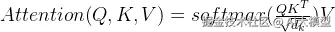
1)核心思想:对于当前要处理的元素Query(例如一个词),决定应该"关注"序列中其他元素Key的多少程度。这个"关注程度"就是一个权重,最终效果:通过点积,注意力机制能够动态地、有针对性地从输入序列中提取最相关的信息,这是Transformer和大型语言模型取得成功的关键突破之一。
2)Query, Key, Value 类比:
Query (查询向量):代表当前元素发出的"提问":"我正在处理,我需要哪些信息?"比喻:就像你在搜索引擎里输入的关键词。
Key (键向量):代表序列中每个元素所拥有的"标签"或"标识"。它用来回应 Query的提问。比喻: 就像互联网上每个网页的关键词标签(索引)。
Value (值向量):代表序列中每个元素实际包含的"信息"或"内容"。比喻: 就像网页本身的完整内容。
3)注意力的工作流程:将当前的 Query 与序列中所有元素的 Key 进行比较。点积就是执行这个比较操作的完美工具!相似度分数 = Query · Key加权:将这些相似度分数通过Softmax函数转换为权重(所有权重之和为1的正数概率分布)。分数越高,权重越大。求和:用这些权重对所有的 Value 进行加权求和,得到最终的注意力输出。
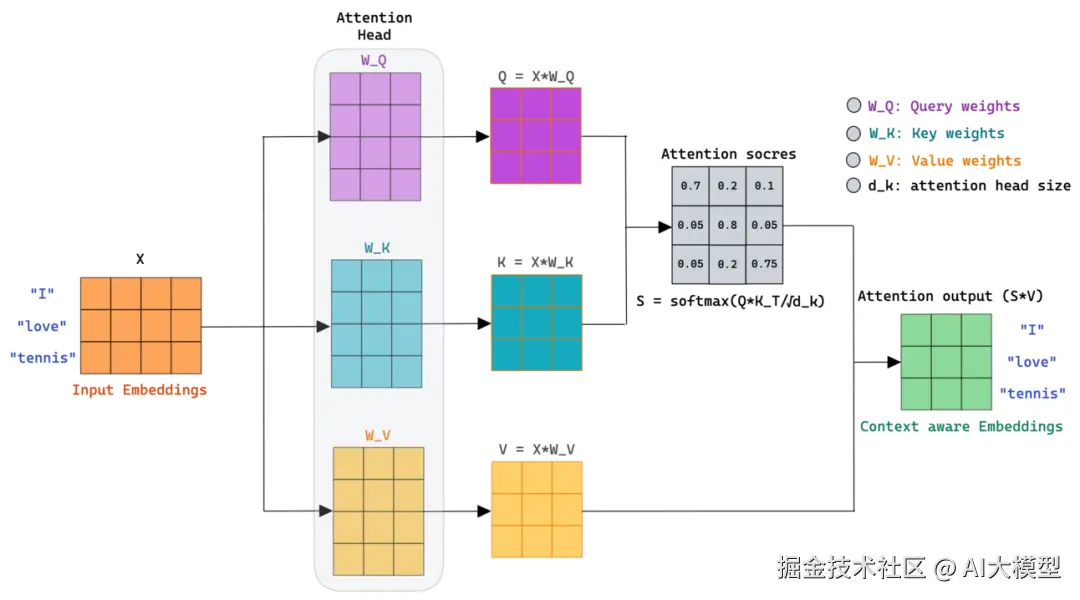
4)为什么点积是计算相似度的完美工具?现在我们结合几何意义来理解:
➢ Query · Key 的值越大 -> 根据点积公式,这意味着 cos(θ) 接近 1 -> 两个向量的方向非常接近 -> 这个Key所对应的元素所拥有的"标签"(Key)与当前的"提问"(Query)高度相关 -> 因此,这个元素应该获得高注意力权重。
➢ Query · Key 的值接近 0 -> cos(θ) 接近 0 -> 两个向量近乎垂直 -> Key 和 Query 不相关 -> 权重应接近 0。
➢ Query · Key 的值为负 -> cos(θ) 为负 -> 两个向量方向相反 -> 可能意味着某种排斥或对立关系 -> 权重会非常小(因为Softmax会将负值压得很低)。
5)既然 cos(θ) 更好,为什么Transformer的论文《Attention Is All You Need》中用的是点积公式 Q · K,而不是直接写 cos(θ) 呢?理解点积受长度影响这一缺陷,是理解为何需要LayerNorm、缩放因子等技巧的关键。架构设计(如LayerNorm)和缩放操作 (/ √d_k) 确保了 (Q · K) 能够有效地充当相似度的度量指标。
➢ 计算效率:点积 Q · K 只需要一次矩阵乘法,计算速度极快。如果先分别计算每个Q和K的模长再做除法,计算成本更高。使用 (Q · K) 是出于计算效率和实现便利的考虑。隐含的假设:在标准的Transformer架构中,Query和Key向量通常已经进行了某种形式的归一化(例如,通过其初始化方式和层归一化LayerNorm),它们的模长被控制在一个较小的范围内波动。因此,点积 Q · K 的结果虽然不完全等价,但已经高度近似于余弦相似度 cos(θ) 所表达的方向相似性。其内在的物理意义,仍然是衡量Query和Key向量方向的相似性(即 cos(θ))。
➢ 可学习的缩放因子:论文中并没有直接使用点积,而是使用了缩放点积注意力(Scaled Dot-Product Attention):注意力分数 =(Q · K) / √d_k)这里除以 √d_k(Key向量的维度)的主要原因之一是:防止点积结果过大,导致Softmax函数的梯度消失问题(因为Softmax会将非常大的输入值推向饱和区)。这个缩放操作进一步稳定了训练。
4.点积运算vs自注意力python实现
在Transformer模型中,自注意力机制(Self-Attention)的核心就是使用点积来计算查询(Query)和键(Key)之间的相似度。具体步骤如下:
1)准备输入:初始化参数,将输入向量转换为Query、Key和Value矩阵
2)计算注意力分数:通过Query和Key的点积计算注意力分数attentionscore
3)缩放:将点积结果除以Key向量维度的平方根(√dₖ)
4)Softmax:对缩放后的分数应用Softmax函数获得注意力权重
5)加权求和:用注意力权重对Value进行加权求和
6)输出结果。
感兴趣的朋友,可以阅读并运行下面代码。
python
import numpy as np
import matplotlib.pyplot as plt
from math import sqrt
#点积计算注意力
defscaled_dot_product_attention(Q, K, V, print_steps=False):
"""
实现缩放点积注意力机制
参数:
Q -- 查询矩阵 (batch_size, num_heads, seq_len, d_k)
K -- 键矩阵 (batch_size, num_heads, seq_len, d_k)
V -- 值矩阵 (batch_size, num_heads, seq_len, d_k)
print_steps -- 是否打印中间步骤
返回:
输出张量和注意力权重
"""
# 1. 计算注意力分数: Q·K^T
# 形状: (batch_size, num_heads, seq_len, seq_len)
matmul_qk = np.matmul(Q, K.transpose(0,1,3,2))
if print_steps:
print("\n步骤1: 计算Q·K^T")
print("Q·K^T 形状:", matmul_qk.shape)
print("示例值(第一个样本,第一个头):\n", matmul_qk[0,0,:,:])
# 2. 缩放注意力分数 (除以sqrt(d_k))
d_k = Q.shape[-1]
scaled_attention_logits = matmul_qk / sqrt(d_k)
if print_steps:
print("\n步骤2: 缩放注意力分数 (除以√d_k)")
print("d_k =", d_k)
print("缩放后形状:", scaled_attention_logits.shape)
print("示例值(第一个样本,第一个头):\n", scaled_attention_logits[0,0,:,:])
# 3. 应用softmax获取注意力权重
# 注意: softmax应用于最后一个维度(seq_len)
attention_weights = np.exp(scaled_attention_logits - np.max(scaled_attention_logits, axis=-1, keepdims=True))
attention_weights /= np.sum(attention_weights, axis=-1, keepdims=True)
if print_steps:
print("\n步骤3: 应用softmax获取注意力权重")
print("注意力权重形状:", attention_weights.shape)
print("示例值(第一个样本,第一个头):\n", attention_weights[0,0,:,:])
print("检查行和(应接近1):", np.sum(attention_weights[0,0,0,:]))
# 4. 将注意力权重与值矩阵相乘
output = np.matmul(attention_weights, V)
if print_steps:
print("\n步骤4: 注意力权重·V")
print("输出形状:", output.shape)
print("示例值(第一个样本,第一个头):\n", output[0,0,:,:5])# 只显示前5个特征
return output, attention_weights
#多头注意力机制
classMultiHeadAttention:
"""
Multi-Head Attention层实现 [[5]]
这个实现将输入分割为多个注意力头,分别计算注意力,然后合并结果。
"""
def__init__(self, d_model, num_heads):
"""
初始化Multi-Head Attention层
参数:
d_model -- 模型维度(输入和输出的维度)
num_heads -- 注意力头的数量
"""
self.d_model = d_model
self.num_heads = num_heads
# 确保d_model可以被num_heads整除
assert d_model % num_heads ==0,"d_model must be divisible by num_heads"
self.d_k = d_model // num_heads # 每个注意力头的维度
# 初始化权重矩阵 (使用Xavier初始化)
self.W_q= np.random.randn(d_model, d_model)/ sqrt(d_model)
self.W_k= np.random.randn(d_model, d_model)/ sqrt(d_model)
self.W_v= np.random.randn(d_model, d_model)/ sqrt(d_model)
self.W_o= np.random.randn(d_model, d_model)/ sqrt(d_model)
print(f"MultiHeadAttention初始化完成:")
print(f"- d_model: {d_model}")
print(f"- num_heads: {num_heads}")
print(f"- d_k per head: {self.d_k}")
print(f"- 权重矩阵形状: W_q={self.W_q.shape}, W_k={self.W_k.shape}, W_v={self.W_v.shape}, W_o={self.W_o.shape}")
defsplit_heads(self, x, batch_size):
"""
将最后一个维度分割为(num_heads, d_k)
参数:
x -- 输入张量 (batch_size, seq_len, d_model)
batch_size -- 批次大小
返回:
重排后的张量 (batch_size, num_heads, seq_len, d_k)
"""
x = x.reshape(batch_size,-1, self.num_heads, self.d_k)
# 交换维度以获得 (batch_size, num_heads, seq_len, d_k)
return np.transpose(x,(0,2,1,3))
defcombine_heads(self, x, batch_size):
"""
将多个注意力头的结果合并
参数:
x -- 分割后的张量 (batch_size, num_heads, seq_len, d_k)
返回:
合并后的张量 (batch_size, seq_len, d_model)
"""
# 交换维度以获得 (batch_size, seq_len, num_heads, d_k)
x = np.transpose(x,(0,2,1,3))
# 合并最后两个维度
return x.reshape(batch_size,-1, self.d_model)
defforward(self, x, print_steps=False):
"""
前向传播
参数:
x -- 输入张量 (batch_size, seq_len, d_model)
print_steps -- 是否打印中间步骤
返回:
输出张量和所有注意力头的注意力权重
"""
batch_size = x.shape[0]
seq_len = x.shape[1]
if print_steps:
print("\n===== Multi-Head Attention 前向传播 =====")
print("输入形状:", x.shape)
print("示例输入(第一个样本):\n", x[0,:,:5])# 只显示前5个特征
# 1. 线性投影得到Q, K, V
Q= np.matmul(x, self.W_q)
K= np.matmul(x, self.W_k)
V= np.matmul(x, self.W_v)
if print_steps:
print("\n步骤1: 线性投影得到Q, K, V")
print("Q形状:", Q.shape,"K形状:", K.shape,"V形状:", V.shape)
print("示例Q值(第一个样本):\n", Q[0,:,:5])
# 2. 分割为多个注意力头
Q= self.split_heads(Q, batch_size)
K= self.split_heads(K, batch_size)
V= self.split_heads(V, batch_size)
if print_steps:
print("\n步骤2: 分割为多个注意力头")
print("分割后Q形状:", Q.shape,"K形状:", K.shape,"V形状:", V.shape)
print("示例Q值(第一个样本,第一个头):\n", Q[0,0,:,:5])
# 3. 计算缩放点积注意力
attn_output, attn_weights = scaled_dot_product_attention(
Q, K, V, print_steps=print_steps
)
# 4. 合并所有注意力头
attn_output=self.combine_heads(attn_output, batch_size)
if print_steps:
print("\n步骤4: 合并所有注意力头")
print("合并后输出形状:", attn_output.shape)
print("示例输出(第一个样本):\n", attn_output[0,:,:5])
# 5. 应用最终的线性变换
output = np.matmul(attn_output, self.W_o)
if print_steps:
print("\n步骤5: 应用最终线性变换 (W_o)")
print("最终输出形状:", output.shape)
print("示例输出(第一个样本):\n", output[0,:,:5])
return output, attn_weights
# 测试实现
if __name__=="__main__":
# 设置随机种子以确保结果可重现
np.random.seed(42)
# 创建示例输入 (batch_size=2, seq_len=3, d_model=8)
batch_size =2
seq_len =3
d_model =8
num_heads =2
print("===== 创建测试环境 =====")
print(f"批次大小: {batch_size}, 序列长度: {seq_len}, 模型维度: {d_model}, 注意力头数: {num_heads}")
# 随机生成输入数据 (模拟词嵌入)
x = np.random.randn(batch_size, seq_len, d_model)
# 创建Multi-Head Attention层
mha = MultiHeadAttention(d_model, num_heads)
# 执行前向传播并打印所有中间步骤
print("\n"+"="*50)
print("开始执行前向传播,打印所有中间步骤...")
print("="*50)
output, attn_weights = mha.forward(x, print_steps=True)
# 打印最终结果摘要
print("\n"+"="*50)
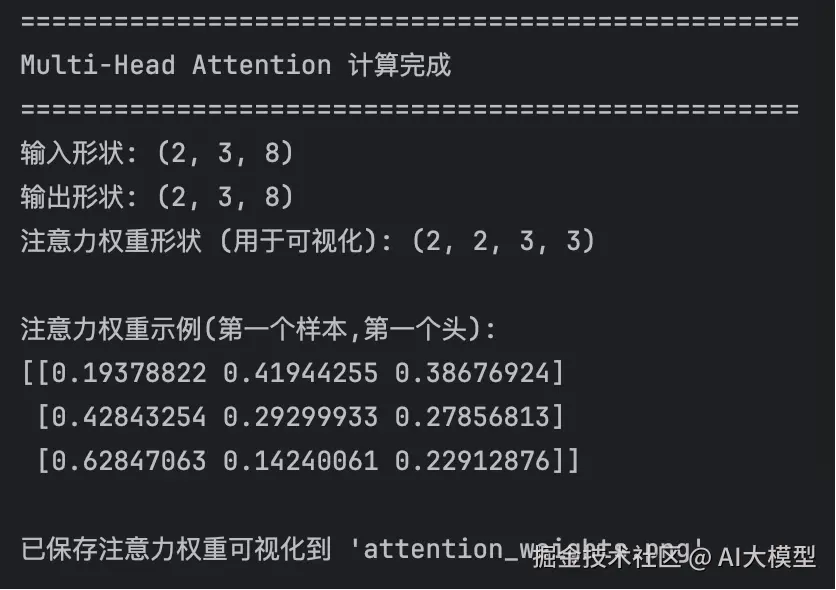
print("Multi-Head Attention 计算完成")
print("="*50)
print("输入形状:", x.shape)
print("输出形状:", output.shape)
print("注意力权重形状 (用于可视化):", attn_weights.shape)
print("\n注意力权重示例(第一个样本,第一个头):")
print(attn_weights[0,0,:,:])
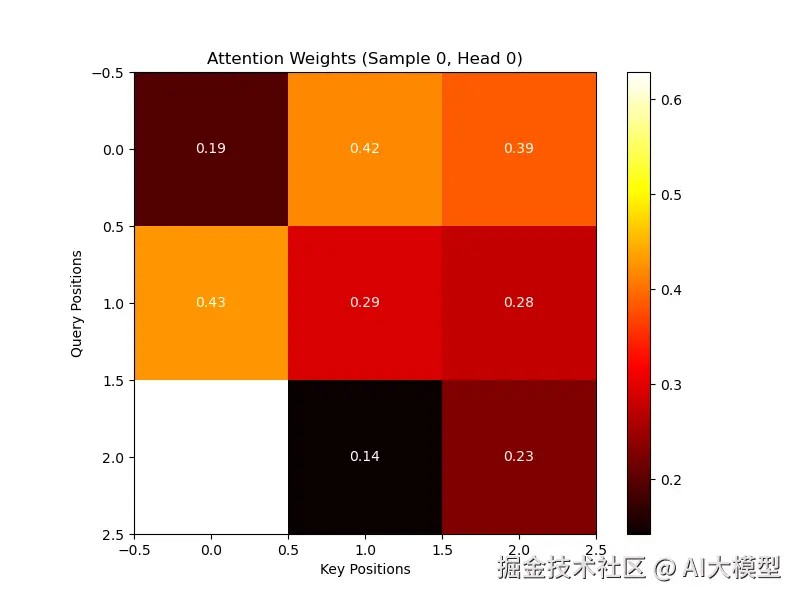
# 可视化第一个样本的第一个注意力头
plt.figure(figsize=(8,6))
plt.imshow(attn_weights[0,0], cmap='hot', interpolation='nearest')
plt.colorbar()
plt.title('Attention Weights (Sample 0, Head 0)')
plt.xlabel('Key Positions')
plt.ylabel('Query Positions')
for i inrange(seq_len):
for j inrange(seq_len):
plt.text(j, i,f'{attn_weights[0, 0, i, j]:.2f}',
ha='center', va='center', color='w')
plt.savefig('attention_weights.png')
print("\n已保存注意力权重可视化到 'attention_weights.png'")学习资源推荐
如果你想更深入地学习大模型,以下是一些非常有价值的学习资源,这些资源将帮助你从不同角度学习大模型,提升你的实践能力。
本文较长,建议点赞收藏。更多AI大模型应用开发学习视频及资料,在智泊AI。